基于改进无迹卡尔曼滤波算法的水下目标跟踪

张 凯

(郑州旅游职业学院机电工程系 河南 郑州 450009)

0 引 言

水下目标的测量噪声很高，需要使用滤波器消除这种噪声，常见的线性系统滤波器有维纳滤波器和卡尔曼滤波器。卡尔曼滤波器是一种应用非常广泛的线性滤波器，能对过程噪声和测量噪声进行最优滤波。但是其前提条件是已知噪声的协方差，过程噪声和测量噪声满足白噪声或者近似为白噪声，且要求两者独立互不相关。但现实世界中系统基本都是非线性的，扩展卡尔曼滤波(Extended Kalman Filter，EKF)和无迹卡尔曼滤波(Unscented Kalman Filter，UKF)是常见的两种非线性滤波系统。EKF是针对非线性系统应用非常普遍的状态估计方法，但是其依赖对非线性系统的线性化来传播状态的均值和协方差，依赖于局部非线性强度，当系统的线性化比较严重时，其估计并不准确。而且在线性化时需要推导复杂的雅可比矩阵，需要计算并保留非线性函数泰勒展开式的一阶近似项，不适用于更高阶的非线性系统。Julier等[1-2]基于近似概率分布比近似非线性函数或非线性变换要相对简单的思想，提出了采用无迹变换(Unscented transformation，UT)结合卡尔曼滤波的无迹卡尔曼滤波算法。该算法不像EKF采用近似系统的非线性函数，而是近似量测方程的概率密度函数，降低了EKF线性化带来的误差，而且相比于EKF具有更小的估计误差。在UKF系统中的，无须计算雅可比矩阵，其状态分布是利用σ点通过非线性函数进行近似变换得到，比EKF更适合用于非线性系统的目标跟踪。

文献[3]提出一种集成无迹卡尔曼，使用常规的最小二乘法先对多个UKF的估计值积分，再进行滤波。该方法没有考虑量测信息的统计特性的权重，因而跟踪的精度有限。马艳等[4]提出自适应调整目标状态噪声的概率分布的无迹卡尔曼滤波，改善了非机动目标的估计性能。但该算法在维数较高的非线性系统中，对概率分布的调整易引起系统发散。高文娟等[5]提出了基于EKF和UKF的交互式多模型的水下机动目标跟踪算法。宋绪栋等[6]提出了基于纯方位角测量的水下目标被动跟踪技术。吴盘龙等[7]提出了基于平方根UKF的水下纯方位目标跟踪，使用协方差平方根代替协方差，解决了无迹卡尔曼滤波算法中误差协方差矩阵负定导致滤波发散的问题。高剑等[8]提出了采用三阶精度获得非线性变换的均值和协方差的估计的无迹卡尔曼滤波算法。邓兵等[9]提出了基于估计偏差修正的扩展卡尔曼滤波算法，减小了局部线性化截断误差对于观测矩阵的影响，但是其增加了系统的计算量。蔚婧等[10]提出了通过曲线拟合前几个时刻的方位角测量序列获得当前时刻目标的估计值对目标参数进行估计的纯方位目标跟踪算法，但该算法的适用范围较窄。吴林煌等[11]采用神经网络对跟踪系统建模，提出基于自适应EKF与神经网络的预失真算法，该算法中的测量误差矩阵的自适应迭代公式复杂度高且计算量大。

因为每个测量值都携带有噪声，而不同设备得到的测量值的精度也各不相同。基于该思想，本文应用多个UKF对目标进行跟踪，设定每个UKF不同的权重，将根据得到的测量值的精度大小而赋予相应的权重，精度高的权重取值较大，反之取值小，再利用加权最小二乘法(Weighted Least Squares,WLS)对测量值进行积分得到改进的无迹卡尔曼滤波(Improved UKF，IUKF)算法。

针对目标的位置和方向，本文将扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)和改进的无迹卡尔曼滤波(IUKF)应用到水下的目标跟踪中，并对算法的可靠性和准确性进行了仿真分析。仿真结果表明，改进的无迹卡尔曼滤波能更有效地对水下目标进行跟踪，比另外两种方法具有较高的位置和方向估计精度。

1 滤波算法

卡尔曼滤波是最优线性滤波，在假定系统模型和噪声统计特性已知的前提下效果很好。但在一般的应用中，大多数都是非线性系统，甚至欧姆定律也是在一定范围内的近似表达式，而且多数系统不容易获得精确的系统模型和测量噪声的统计特性。因为自然界的噪声往往是非高斯或者近似高斯的，而且存在重尾效应，需要对其进行修正以适应这种可能性。

1.1 扩展卡尔曼滤波

在实际工程应用中，非线性系统的情况较多，所以常常不能满足应用卡尔曼滤波的前提条件，如果应用卡尔曼滤波，容易使滤波发散和精度下降。扩展卡尔曼滤波是比其他非线性滤波较为简便且应用广泛的一种方法，用简单的算法即可获得较好的结果。

离散时间非线性系统及其EKF递推步骤如下[12]：

步骤1系统状态方程和测量方程：

xk=fk-1(xk-1,uk-1,wk-1)yk=hk(xk,vk)

(1)

式中：f(·)和h(·)分别表示系统状态函数和测量函数；xk和yk分别为k时刻的状态值和测量值；wk和vk为状态噪声和测量噪声，其均值均为0，协方差分别为Qk和Rk，且二者互不相关。

步骤2初始化滤波如下：

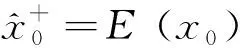
(2)

步骤3循环k=1，2，…，完成步骤4至步骤7。

步骤4计算偏微分(雅可比矩阵)矩阵(如果状态方程是线性的，可跳过此步骤)：

(3)

步骤5状态估计和估计误差协方差的时间更新：

(4)

步骤6计算如下偏微分矩阵：

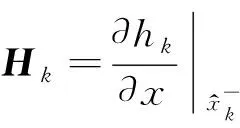
(5)

步骤7状态估计的测量更新和估计误差协方差的更新如下：

Pk+=(I-KkHk)Pk-

(6)

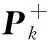
1.2 无迹卡尔曼滤波

非线性系统的概率密度函数很难通过一般的非线性函数求解。虽然EKF和迭代EKF求解均值和协方差的线性化变换近似等同于真实的非线性变换，但仅仅是在较简单的二维情况下近似成立。当系统的维数大于二维的时候，EKF和迭代EKF的估计误差会急剧增大。而无迹卡尔曼滤波能较好地解决这个问题，得到满意的近似结果。无迹卡尔曼滤波的思想是：因为相对于整个概率分布函数来说，对单一点执行非线性变换是比较容易的，所以可以在状态方程中找一组点(称为sigma点)，再将sigma点经过已知的非线性函数y=h(x)变换，得到变换后的均值和协方差，再估计出y的真实均值和方差，从而来近似状态向量的真实概率分布函数。

无迹卡尔曼滤波简要步骤如下[12]：

设满足N维离散非线性系统为(假设状态方程和测量方程相对噪声是线性的)

xk+1=f(xk,uk,tk)+wkyk=h(xk,tk)+vk

(7)

步骤1初始化：

(8)

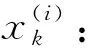
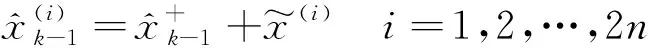
(9)

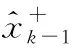
步骤3时间更新：

(10)

步骤4量测更新：

(11)

2 系统状态方程和量测方程

2.1 系统状态方程

假设系统做匀加速运动，目标的初始位置为(x0,y0)，k时刻的位置为(xk,yk)，x轴和y轴方向的速度分别为vx,k、vy,k，初始速度为(vx,0,vy,0)，k时刻的速度为(vx,k,vy,k)，x轴和y轴方向的加速度分别为ax,k、ay,k。即X(k)=[xk,yk,vx,k,vy,k,ax,k,ay,k]T，其状态变量中的关系分别为(其中T为采样时间)：

xk=x0+vx,kT+0.5ax,kT2yk=y0+vy,kT+0.5ay,kT2vx,k=vx,0+ax,kTvy,k=vy,0+ay,kT

(12)

则目标系统的运动状态方程为：

X(k+1)=ΦX(k)+w(k)=

(13)

式中：Φ为系统状态转移矩阵，w(k)为系统状态噪声。

2.2 系统量测方程

假设声呐系统所在的位置为坐标原点，对目标M进行跟踪，可以得到目标M和声呐之间的距离及角度。模型如图1所示。

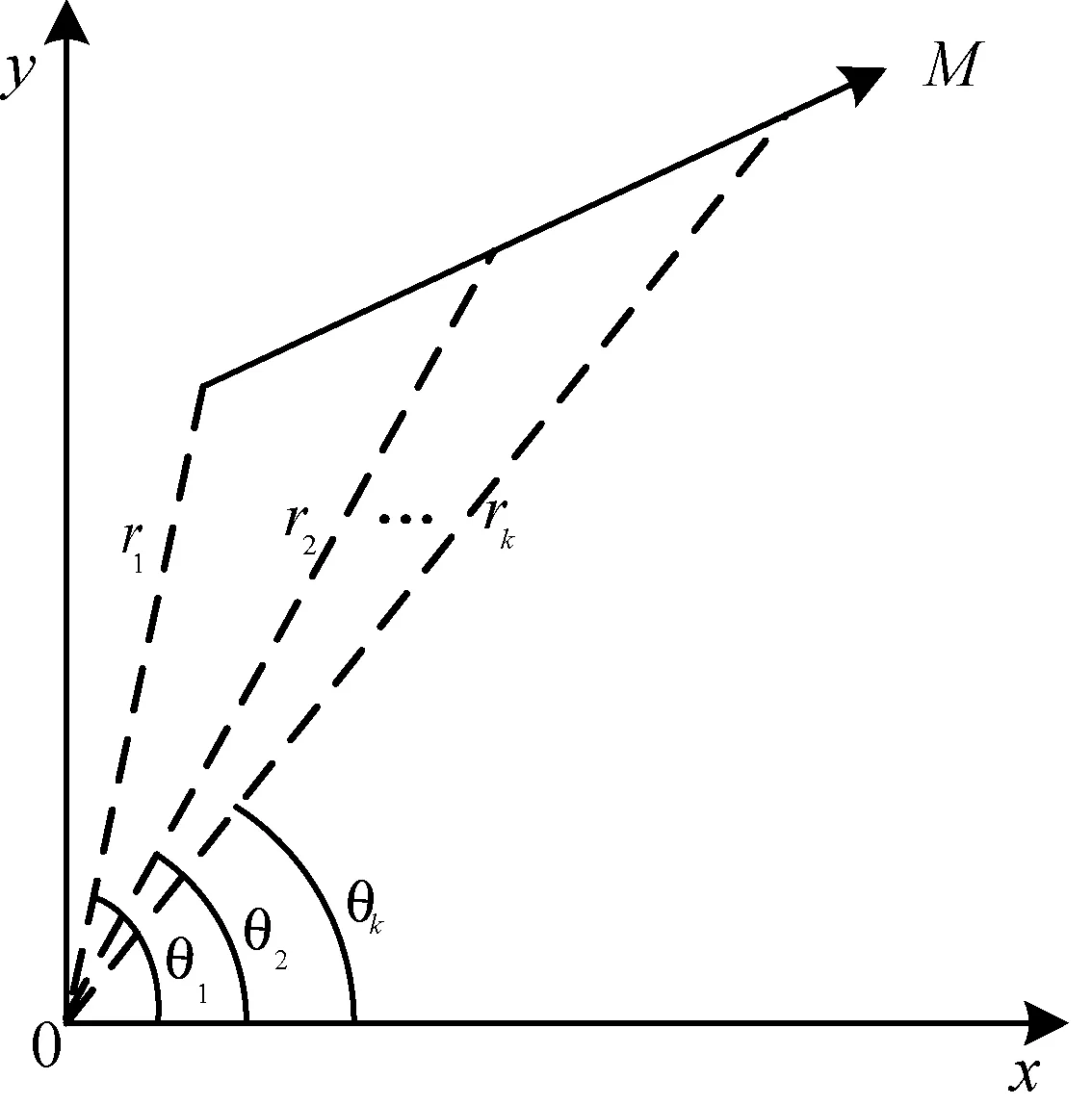
图1 量测模型

由该声呐系统获得目标的离散距离rk和方位角θk，则在该直角坐标系中，系统的量测方程为：

Y(k+1)=h(X(k))+v(k)=

h(r(k),θ(k))+v(k)=

(14)

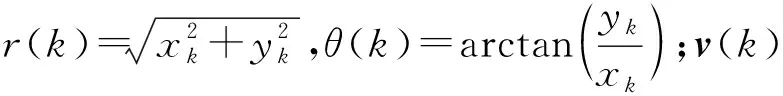
由式(14)可以知道该模型的状态方程是线性的，量测方程是非线性的。在对系统应用EKF时，需要计算量测方程的雅可比矩阵为：

(15)

2.3 改进的UKF(IUKF)

(16)

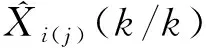
Pi(k/k)=diag[Pi1Pi2…Pin]

(17)

Pij是第i个UKF给定的状态向量X的第j个元素的估计方差。则：

(18)

式中：Ri(k)是高斯噪声的p×1矩阵，是第p个UKF给出的估计的第i个元素，其均值为零的协方差矩阵。设每个测量值的噪声都是零均值且相互独立，设测量噪声为vi，则：

(19)

测量噪声的协方差矩阵为：

(20)

为了得到测量值，使式(21)最小。取回归函数为：

(21)

(22)

进而得到式(22)的解的形式：

(23)

3 仿真结果及分析

为了对比验证IUKF与EKF、UKF两种算法的性能，进行100次Monte Carlo数值仿真实验，比较其滤波结果的均方根误差(RMSE)。仿真基于以下的假设：声呐所在的位置为坐标原点，假设系统目标在水下的深度恒为35 m，在这个平面内做匀加速运动，目标开始位置为(1 000,1 000)，x方向的初速度为20 m/s，y方向的初速度为40 m/s，x方向的加速度为3 m/s2，y方向的加速度为-3.6 m/s2，仿真总时间t=50 s，采样时间间隔T=0.5 s，状态噪声wk和测量噪声vk二者互不相关，其协方差Qk和Rk分别如下：

(24)

(25)

应用EKF、UKF和IUKF三种方法滤波的结果如图2至图4所示。图2是对目标运动轨迹的仿真对比，可以看出IUKF比EKF、UKF更接近于真实的运动轨迹。图3是对目标位置跟踪误差的仿真。图4是对目标运动速度跟踪误差的仿真。表1给出了三种方法滤波后位置、速度的均方误差对比。可以看出，IUKF的跟踪误差小，滤波误差曲线收敛较快。这是因为EKF、UKF将目标的非线性测量方程近似为一个线性滤波问题，然后套用线性滤波求解原非线性滤波问题，其滤波的稳定性及状态的估计精度不但与过程噪声和量测噪声的统计特性关系很大(如这里假设Qk和Rk在滤波过程中一直不变，如果设定的值不太准确，易产生误差积累，导致滤波发散)，而且与状态方程及量测方程中的非线性因子有关，是一种次优的滤波算法。而IUKF是使用UT变换处理非线性的，不用求解其量测方程的雅可比矩阵来对其进行近似的线性化，而是对状态向量的概率密度函数进行的，而近似后的概率密度函数还是满足高斯分布的，因而其滤波效果较好，具有更好的滤波精度，但其计算量却与EKF、UKF相近。

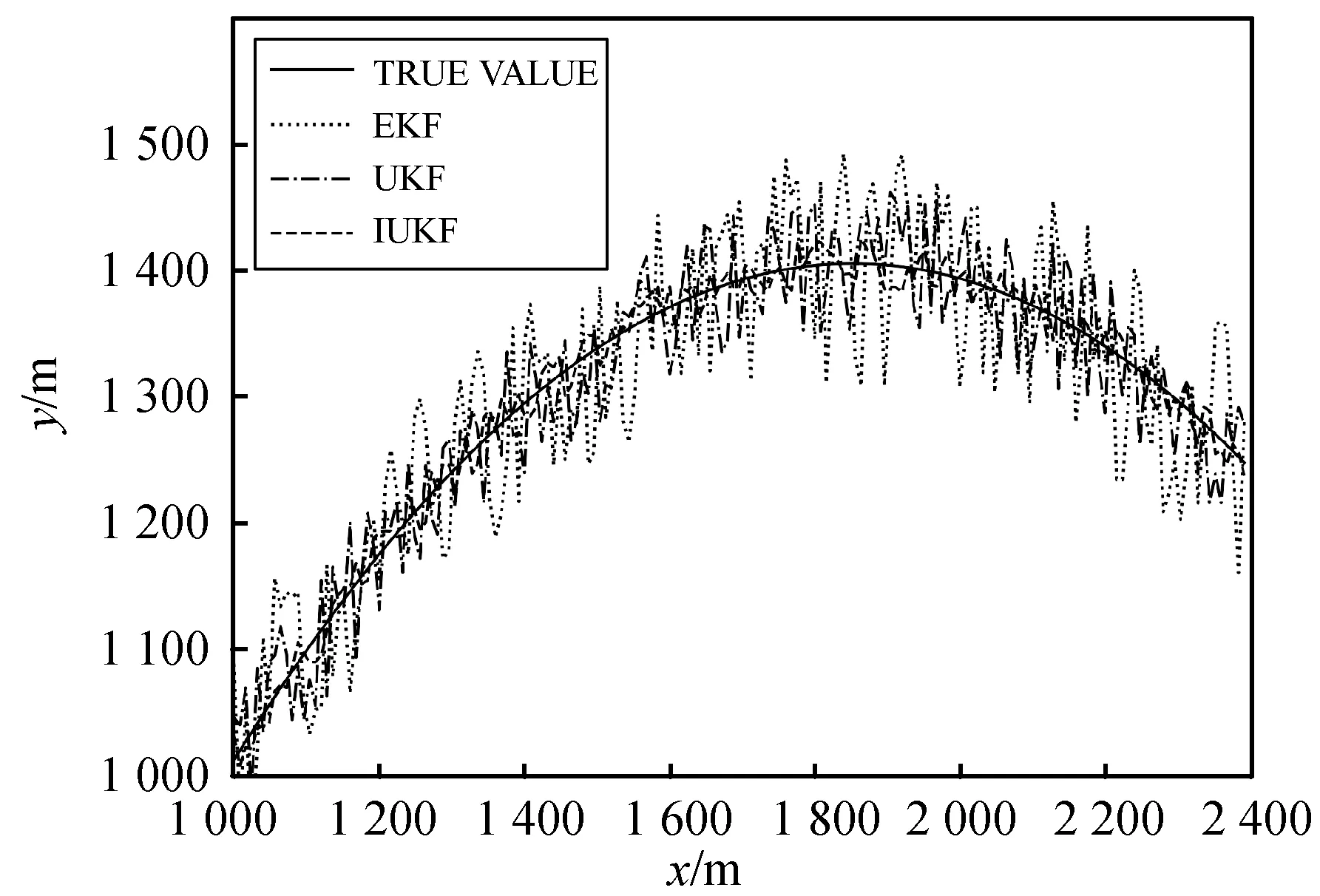
图2 目标运动轨迹

图3 滤波算法的位置跟踪误差

图4 滤波算法的速度跟踪误差

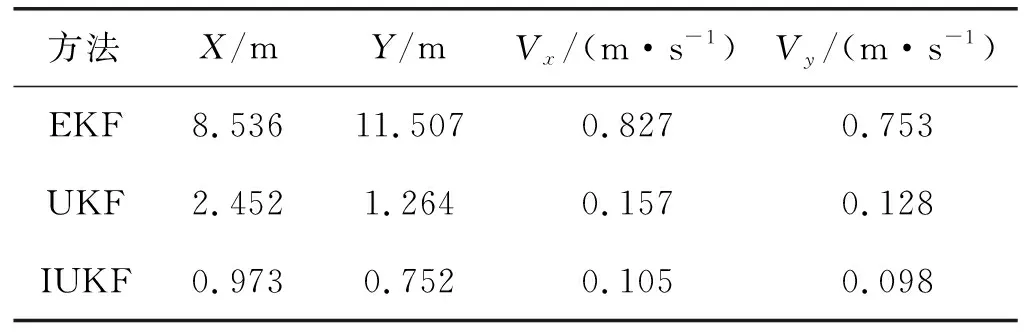
表1 三种方法状态估计的RMSE比较

4 结 语

本文以水下机动目标跟踪为应用背景，提出了一种改进的无迹卡尔曼滤波算法(适用于非线性应用)跟踪估计水下目标运动参数的方法，在确定目标的初始距离和方位的情况下对目标运动进行了仿真，并和EKF、UKF进行了跟踪结果对比，验证了IUKF算法在有效性、测量误差及机动性方面优于EKF、UKF，表明该方法可方便地应用于水下目标的跟踪，比EKF、UKF更加适合对水下机动目标的跟踪。另外，尽管IUKF的估计精度比EKF、UKF高，但IUKF不能应用于非高斯分布系统，而粒子滤波可以解决这一问题。