全高位布置汽轮机机组调节系统参数特性分析

2022-10-09闫晓沛唐广通李路江王志强张

河北电力技术 2022年4期

闫晓沛唐广通李路江王志强张营

(国网河北能源技术服务有限公司,河北石家庄 050021)

电力系统稳定分析是电网规划、研究的重要方法。原动机及其调节系统参数实测与建模是为了建立和规范电力系统并网机组参与电网一次调频的数学模型,为电力系统的中长期稳定性仿真分析提供真实可靠的数据[1]。机组全高位布置在世界范围属于新型机组布置形式,并因其工程总投资少、经济性高的优点相继在国内建成,2021年有2台全高位布置机组及1台高低位布置机组投产发电。全高位布置机组布置较常规机组有明显变化,从而对机组原动机及调节系统模型参数产生影响。本文以世界首例全高位布置机组为研究对象,搭建汽轮发电机组及调节系统模型,通过机组参数测试试验,辨识并建立全高位布置机组的数学模型,进一步研究了全高位布置机组模型参数特点及一次调频特性。

1 全高位布置机组特点

全高位布置超超临界汽轮发电机组将汽轮发电机组的高压缸、中低压缸以及发电机从常规13.7 m 提升到65 m 高度,靠近锅炉过热器出口联箱处,乏汽直接从汽轮机低压缸排至空冷凝汽器蒸汽分配管。由于汽轮机采用高位布置,汽轮机整体靠近过热器及再热器进、出口联箱,因此四大管道长度均减小;机组取消了传统空冷机组的排汽装置,低压缸排汽通过排汽管道从机房7层(42 m 标高)直接排至空冷岛,从而缩短了排汽管道,减小了机组排汽压损;汽轮机采用全高位布置使机组的抽汽回热管道显著增长,受到设备布置标高影响,汽轮机各抽汽管道至抽汽逆止阀距离也相应增加,变相增加了汽轮机缸体的容积,造成机组缸体容积时间常数变化。汽机房共分10层,其全高位布置超超临界机组主要设备布置示意见图1。

图1 全高位布置超超临界机组主要设备布置示意

2 汽轮机组及其调节系统模型

根据某全高位布置超超临界汽轮机组及调节系统的工作原理,其数学模型由调节系统、执行机构、汽轮机、锅炉、发电机及励磁系统模型组成[2-5],其模型框图见图2。根据机组不同的工况和控制方式,调节系统模块通过测量环节接受转速、功率等参数变化,经PID 控制环节及转速不等率环节输出总阀位控制指令;执行机构模块接受调节系统指令,通过自身闭环控制,调整当前机组阀门开度;锅炉主蒸汽压力模块接受机组阀门开度信号及当前机组流量信号,输出主蒸汽压力信号,并根据当前主蒸汽压力及阀门开度生成主蒸汽流量信号;原动机模块接受主蒸汽流量信号,输出机组机械功率,最终通过发电机及励磁系统模块输出发电机功率。

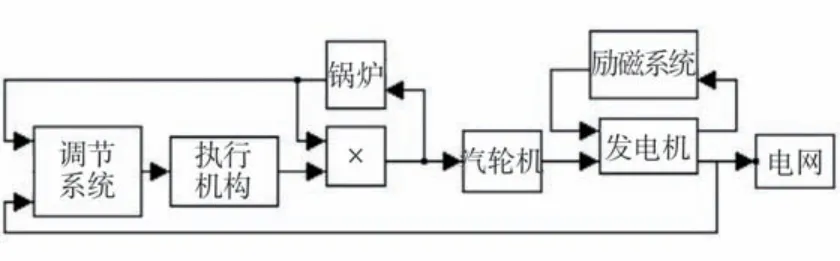
图2 汽轮机及其调节系统模型框图

建模主要用于电网稳定性分析,汽轮机组及其调节系统模型采用DL/T 1235-2019《同步发电机原动机及其调节系统参数实测及建模导则》(简称“导则”)中定义的模型。目前常用的电力系统计算程序灵活性不强,不能利用参数测试试验采集的频域或时域测试数据作为当前辨识模块的输入/输出信号,无法实现各模块或参数的分别辨识,需要解耦不同参数产生的耦合影响以提高模型的仿真精度。为此建模时模型主结构采用导则中定义的模型,各分模块采用专用软件分别辨识,整体模型采用电力系统计算程序校核,使模型与目前常用的电力系统计算程序通用,便于后期校核。

2.1 汽轮发电机组电液调节系统模型

汽轮机及其调节系统模型采用导则中定义的模型,包括含高压缸功率过调系数的汽轮机模型、汽轮机电液控制系统调节系统模型、电液伺服系统模型。同时考虑到全高位布置汽轮机采用高位布置,汽轮机整体靠近过热器及再热器进、出口联箱,四大管道长度均减小会影响容积时间常数,因此要建立锅炉实测模型。汽轮发电机组电液调节系统模型见图3。

图3 汽轮发电机组电液调节系统模型

2.2 单机无穷大系统建模

发电机、励磁系统及电力系统具有较强的非线性特征,文献[6-7]以某发电机模型为例,给出了用于描述其特征的数学方程式。由于发电机模型的数学方程十分复杂,为了简化仿真过程,可以根据电力系统的输出、输入在扰动作用下的关系,从全阶模型中抽取出线性化的低阶模型,从而得到相关的传递函数,在仿真程序中构建实际机组的单机无穷大系统模型(可以不包括汽轮机调节系统模型),并通过仿真参数设置,仿真机械功率阶跃变化时电磁功率的阶跃响应,从而得到系统的输入、输出数据,实现电力系统的快速建模仿真。

电力系统研究中,Prony分析的思想指出,根据输出、输入在扰动作用下的关系,从全阶模型中抽取出线性化的低阶模型,得到相关的传递函数[8-10]。低阶传递模型(s)为

式中:PE为电磁功率;PM为机械功率;ωn为系统自然振荡频率;ξ为系统阻尼系数。本文根据实际电网数据,建立机组对应的单机系统模型,通过Prony分析,确定式(1)中的参数,此时ωn=10.784 rad/s,ξ=0.109。最终的传递函数为

结合电力系统特点,选择过程模型(Process modles)中的欠阻尼模型(Under damped),其传递模型(s)为

式中:K为比例系数;TW为振荡环节的时间常数;TZ为一节微分环节时间常数。辨识结果为K=1,TW=0.093 465,TZ=0.011 907,ξ=0.106 98,最终的传递函数为

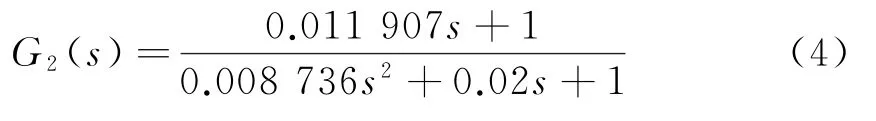
对不同的辨识结果G1(s)和G2(s)进行相似度分析,图4 为模型仿真相似度对比界面,其中P2U 为G1(s)的仿真相似度,相似度97.53%,P2ZU 为G2(s)的仿真相似度,相似度99.32%。结果显示,采用G2(s)作为传递函数能够更好地仿真已知的电力系统。

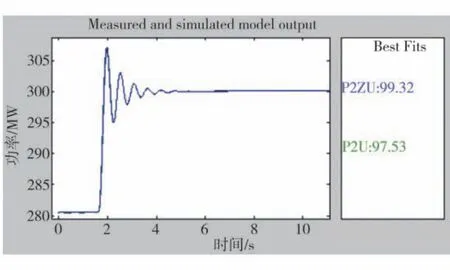
图4 2种单机无穷大系统模型仿真相似度对比

本文采用G2(s)作为传递函数,用于汽轮机调节系统建模与仿真的电力系统模块。

3 全高位布置超超临界机组参数实测及分析

该全高位布置超超临界机组汽轮机采用全周进汽调节,无调节级及补气阀,一次调频采用高调阀节流调节,参数实测采用时域测量法,静态试验中调节系统、执行机构的实测建模与常规布置并无差异。本文主要介绍负载试验,为保证试验准确性,负载试验前需要完成机组阀门流量特性试验、一次调频试验,确保阀门流量特性设置与实际吻合,一次调频功能正常,为保证协调方式下试验的安全及精度,需要完成机组负荷扰动试验,确保机组协调控制性能良好。

3.1 锅炉主蒸汽压力模型参数辨识

锅炉主蒸汽压力模型参数辨识在机组80%负荷、采用阀控方式下频差-负荷阶跃响应的数据,以实测总阀位数据作为锅炉主蒸汽压力模型输入,对锅炉主蒸汽压力模型参数进行单独辨识,机组负荷试验过程中锅炉主蒸汽压力波动值最大达到2.1 MPa,可见全高位布置超超临界机组负荷及主蒸汽流量的扰动对锅炉主蒸汽压力的响应相当明显,反之,主蒸汽压力的大幅波动必然对机组负荷产生影响,因此为保证建模的准确性,需要建立锅炉主蒸汽压力模型。在机组建模及参数辨识过程中,应首先对锅炉容积时间常数、过热器时间常数、过热器流量系数等重要参数进行辨识,确保锅炉主蒸汽压力模型准确的前提下在进行后续仿真,仿真锅炉主蒸汽压力模型时,应以实测总阀位作为锅炉主蒸汽压力模型输入型号,以提高仿真精度。

主要辨识参数结果:锅炉过热器时间常数17 s、锅炉容积时间常数75 s、过热器流量系数3。主蒸汽压力仿真与实际响应值比较见图5。

图5 主蒸汽压力仿真与实际响应值比较

3.2 高压缸前汽室、再热器容积时间常数辨识

参照导则建立高压缸前汽室、再热器容积环节模型见图6,由于该汽轮机无调节级,且试验期间无高压调门后压力测点,无法对高压缸容积时间常数进行辨识。考虑到虽然高压缸容积时间常数实际值比较小,但压力变送器时间常数值相对较大,从而会造成仿真精度较低。根据模型不同参数对功率影响的敏感度分析,高压容积时间常数影响功率初始响应,对功率稳定值无影响。为此采用基于功率初始响应的高压容积时间常数辨识方法,以阀门开度为输入、初始变化功率为输出辨识得到高压缸容积时间常数TCH为0.1 s。在再热器容积时间常数仿真时,将高压缸容积、再热器容积环节模型连接,将实际主蒸汽压力与实际综合阀位的乘积作为输入、再热压力作为输出,辨识得再热器容积时间常数TRH为34.5 s,再热蒸汽压力仿真与实际响应值比较见图7。

图6 高压缸前汽室、再热器容积环节模型

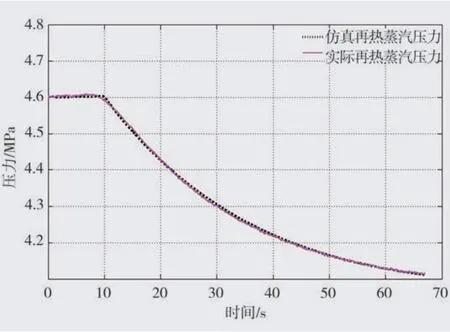
图7 再热蒸汽压力仿真与实际响应值比较

3.3 模型仿真

在完成以上工作的基础上,根据设计参数设置仿真模块仿真参数,对机组进行汽轮机数字电液控制系统(DEH)阀控及协调控制(CCS)投入方式下频差-负荷阶跃响应的整体仿真,图8、9分别为DEH 阀控及CCS方式下频差-负荷阶跃响应值比较。通过仿真数据与实际负荷比较证明仿真精度比较高。

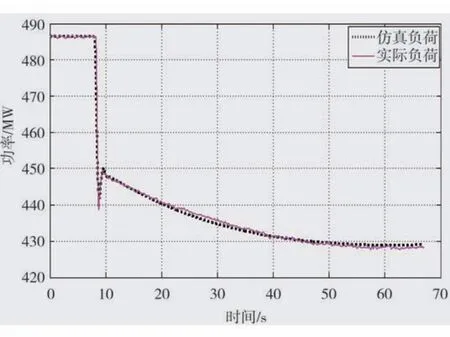
图8 DEH阀控方式下频差-负荷阶跃响应值比较

图9 CCS方式下频差-负荷阶跃响应值比较

3.4 全高位布置超超临界机组参数特性分析

该全高位布置超超临界机组实测模型参数中,锅炉过热器时间常数及过热器流量系数与常规布置机组无明显差异,但较常规布置机组锅炉容积时间常数明显偏小,仅为75 s,再热器容积时间常数明显增大,达到34.5 s。锅炉过热器时间常数及过热器流量系数并未因全高位布置形式而减小,说明高位布置对以上2个参数并无明显影响,而再热器容积时间常数增加的主要原因为,本机组锅炉设计再热蒸汽温度为623 ℃,为此锅炉厂家在原有基础上增加了再热器管道及换热面,从而造成再热器容积时间常数显著增大。超超临界直流锅炉并无汽包,且锅炉容积及蓄热均低于常规机组,加之高位布置的设计形式,所以锅炉容积时间常数显著降低。