基于误差估值累加开环校正的诱导式欺骗检测方法

钟伦珑，刘炅坡，刘永玉

（中国民航大学天津市智能信号与图像处理重点实验室，天津 300300）

0 引言

全球导航卫星系统（global navigation satellite system，GNSS）为民用航空领域提供覆盖全球的高性能定位、测速和授时信息。目前，机载区域导航采用组合导航体制，融合民用GNSS信号、惯性导航系统（inertial navigation system，INS）导航信息和陆基导航信息，提供可靠导航。由于民用GNSS信号码字信息与信号结构公开，GNSS易受蓄意的欺骗式干扰影响[1]。根据生成原理的不同，欺骗式干扰可分为转发式欺骗干扰和生成式欺骗干扰。欺骗式干扰可使航空器偏离期望轨迹[2]，及时有效地检测是否存在欺骗式干扰对于航空运行安全至关重要。根据欺骗检测数据来源的不同，欺骗式干扰检测技术分为基于信号处理的检测技术[3-4]和基于信息解算的检测技术[5-6]。相较于基于信号处理的检测技术，基于信息解算的检测技术无须改变接收机的结构，其将检测算法嵌入机载组合导航算法中，提高了算法检测性能，并易在区域导航计算机中实现。

相对于转发式欺骗干扰，生成式欺骗干扰隐蔽性更强，难以检测。生成式欺骗干扰源通过雷达等监视方法，实时跟踪航空器运动，并按一定规律施加伪距欺骗量，生成欺骗式干扰。当伪距欺骗量没有突变，而是按一定速率变化时，即可生成更难检测的诱导式欺骗干扰。近年来，诱导式欺骗干扰检测技术受到广泛关注。2017年，文献[7]将序贯概率比检测（sequential probability ratio test，SPRT）算法应用到组合导航中，并将GNSS伪距残差作为检测量，提出一种基于SPRT算法的欺骗式干扰检测方法。但是，由于组合导航的误差跟踪作用，在诱导式欺骗干扰影响下，伪距残差会逐渐偏离真实值，该方法对伪距欺骗量较小的诱导式欺骗干扰检测性能不佳。2018年，文献[8]提出了一种基于多径估计延迟锁定环（multipath estimation 2elay locke2 loop，MEDLL）算法改进的GNSS/INS组合导航模式，能够实现欺骗信号的辨识和抑制，保证组合导航信息的可靠性，但这种方法对MEDLL的信号跟踪能力要求高，使用传统的MEDLL导航系统无法长时间保持准确的定位结果输出，导致针对欺骗式干扰的检测性能下降。2018年，文献[9]根据诱导式欺骗对单星紧组合和多星紧组合的拉偏能力不同，通过对比两种导航输出的定位结果进行诱导式欺骗干扰检测，但这种方法对惯性传感器的精度要求高，若采用低精度的惯性传感器，单星紧组合的滤波结果会出现异常变化，产生错误的检测结果。2022年，文献[10]结合机载多传感器体制的优势，利用闭环紧组合导航输出的GNSS、INS导航数据以及不受欺骗式干扰影响的测距仪（2istance measuring equipment，DME）的导航数据，提出了基于自适应SPRT的机载欺骗式干扰检测方法，该方法在一般情形下有效。在欺骗干扰源的监视方法可精确定位航空器，并准确施加微小的伪距欺骗量的“最坏”情形下，在闭环紧组合导航滤波过程中，受欺骗的GNSS不断校正INS，导致INS被欺骗“污染”，造成“最坏”情形下该方法检测率较低且容易产生漏警。

针对这种“最坏”情形下的诱导式欺骗检测问题，本文从紧组合的校正机制入手，设计了一种周期校正的误差估值累加开环校正结构进行欺骗式干扰检测。首先，分析了周期校正的误差估值累加开环校正结构与传统闭环校正结构导航结果的等效性。其次，利用周期校正的误差估值累加开环校正结构下GNSS导航信息和不被欺骗“污染”的其他导航信息为自适应SPRT机载欺骗干扰检测方法提供检测信息，进行诱导式欺骗干扰检测。最后，对本文方法的有效性进行仿真验证。

1 基于伪距测量的诱导式欺骗干扰模型

GNSS诱导式欺骗干扰的根本目的是对用户接收机造成恶意攻击，通过附加小的伪距欺骗量，在不易被检测的情况下使目标航空器的导航系统产生错误定位，从而导致航空器的自动飞行控制系统根据被欺骗的定位信息逐渐拉偏航空器，最终导致航空器偏离预定航迹。

根据GNSS基本原理[11]，正常情况下，用户接收机P与第j颗可见卫星的伪距测量值ρGNSS,j为：

其中，rGNSS,j为第j颗可见卫星与用户接收机P之间的距离，δ tGNSS为GNSS接收机时钟误差，c为光速，vp为接收机内部噪声与GNSS测量噪声总和，vp～ N (0,σG

2NSS)，σGNSS为伪距测量噪声标准差。

当存在诱导式欺骗干扰时，受欺骗干扰源施加的伪距欺骗量的影响，第j颗可见卫星的伪距测量值变为：

其中， Δρj= a (t -ts)+ b+ ωΔρ为欺骗式干扰引入的附加伪距，a为伪距诱导速率，b为恒伪距欺骗量，ωΔρ为欺骗干扰源监视误差造成的实际附加伪距欺骗量与预期附加伪距欺骗量的偏差，t为当前导航时间，ts为欺骗发生时间。在“最坏”情形下，诱导式欺骗干扰源的监视方法可精确定位航空器[12]，欺骗干扰源从零开始缓慢增加附加伪距欺骗量，即伪距诱导速率a为非零小数，而恒伪距欺骗量b和由监视误差造成的偏差ωΔρ为0。

2 误差估值累加开环校正的紧组合结构

常见的欺骗式干扰检测技术基于现有机载导航体制，采用开环校正的紧组合导航系统[7]，工程实现简单。不同于闭环校正结构，开环校正系统受到诱导式欺骗后，INS的工作不会受到影响，短期内可有效提高欺骗检测性能，但是存在INS随时间累积的误差导致的组合导航滤波器发散问题。针对此问题，本文设计了一种周期校正的误差估值累加开环校正结构进行欺骗式干扰检测。

2.1 误差估值累加开环校正结构

周期校正的误差估值累加开环校正结构如图1所示。与传统开环校正结构不同，本文结构在紧组合导航滤波器输出端增加了一个误差累加器，累加紧组合导航滤波器各滤波时刻输出的估计误差，周期性地校正INS和GNSS内部参数。根据ICAO附件10对机载设备巡航阶段的30 s告警时间要求[13]，将误差估值累加开环校正结构的校正周期设为30 s。图1中，在单个校正周期内，每隔0.5 s紧组合导航滤波更新一次；在①处和②处将误差累加器中累加的各滤波时刻INS和GNSS误差估值分别与INS和GNSS的输出进行误差抵消，但不进行INS和GNSS内部参数校正；在③处计算伪距、伪距率量测值，并将其作为紧组合滤波器下一次滤波的输入。当时间达到校正周期时，使用累加的误差估值对INS和GNSS内部参数进行校正，并对误差累加器清零。从时间上分析，与传统的闭环和开环校正结构相比，本文结构能达到以下效果。

图1 周期校正的误差估值累加开环校正结构

短期内，在每个校正周期内，本文结构与传统开环校正结构相同，不使用误差估值对INS内部参数进行校正，INS不会被校正周期内可能发生的诱导式欺骗“污染”。

长期来看，本文结构周期性地对INS内部参数进行了校正，抵消了INS随时间累积的误差，达到和传统闭环校正结构相同的校正效果，滤波结果不会因INS随时间累积的误差而发散，保证了作为机载导航基准的INS自身的导航结果长期可用。

从工作原理分析，本文结构将原本用于闭环校正的误差估值累加，使累加的误差估值与INS、GNSS子系统误差同步增加，在两个子系统输出端抵消校正后，将二者做差形成较小的滤波器输入量，保证了线性滤波方程微小量误差假设成立。同时，在一个校正周期内，这种抵消校正仅在子系统输出端进行，可获得欺骗信息，到达校正周期时才校正子系统内部导航参数。因此本文校正结构既校正了INS随时间累积的误差，又可以提供未被诱导式欺骗“污染”的欺骗检测信息。

2.2 校正结构等效性分析

为了将周期校正的误差估值累加开环校正结构用于现有机载导航体制中，需要保证其导航输出结果与现有闭环校正结构的导航输出结果一致，因此本节对其校正结构的等效性进行分析。

INS/GNSS紧组合闭环校正结构如图2所示，在每次滤波后都将滤波器输出的误差估值反馈回INS和GNSS，校正其内部状态参数。

图2 INS/GNSS紧组合闭环校正结构

分析周期校正的误差估值累加开环校正紧组合的导航输出结果与现有闭环校正结构紧组合的导航输出结果是否一致，可等效为分析在整个校正周期内的某一滤波时刻，图1与图2所示紧组合导航输出是否相等。

设校正周期包含K个滤波时间间隔Δt，校正周期的起始滤波时刻为t0，终止滤波时刻为tK。

在图2所示的INS/GNSS紧组合闭环校正结构中， 各滤波时刻的各子系统状态变量为Xi(i= 0,1,2,…, K - 1,K)，相邻滤波时刻状态变量 Xi的变化量为ΔXi，各滤波时刻滤波器输出的滤波误差估值为，各滤波时刻的先验状态向量为，各滤波时刻的后验状态向量为，后验状态向量为状态变量经过闭环校正后的紧组合导航输出。

根据闭环卡尔曼滤波原理[14]，可以得到如下关系。

由式（7）可见，tp时刻图2紧组合导航输出等于在校正周期内图1中不加校正的INS状态输出与各滤波时刻输出的误差估值累加之差，由此证明本文设计的周期校正的误差估值累加开环校正紧组合的导航输出结果与现有闭环校正结构紧组合的导航输出结果一致，周期校正的误差估值累加开环校正结构与现有闭环校正结构具有等效性。

3 开环校正结构下的欺骗检测系统及方法

基于机载多传感器导航体制，利用其他导航系统信息，可提升欺骗式干扰检测效果。文献[10]提出的自适应SPRT机载欺骗式干扰检测方法融合了不受欺骗影响的DME导航信息，增加了欺骗检测信息的可靠性。在一般情形下，该方法能够有效检测诱导式欺骗，但针对欺骗干扰源监视方法可精确定位航空器的“最坏”情形，其检测效果不佳。

3.1 误差估值累加开环校正欺骗检测系统

将文献[10]的闭环校正结构改变为本文提出的周期校正的误差估值累加开环校正结构，可在保证滤波器不因INS随时间累积的误差而发散的前提下，避免INS被欺骗式干扰“污染”，从而提高“最坏”情形下的检测性能。本文设计的误差估值累加开环校正欺骗检测系统结构如图3所示，在可软件实现的检测模块中，可使用不同的欺骗式干扰检测方法，融合本文开环校正结构输出的未受诱导式欺骗“污染”的INS惯性导航信息、GNSS信息与DME导航信息，进行欺骗检测统计量计算、判断是否受到欺骗式干扰。

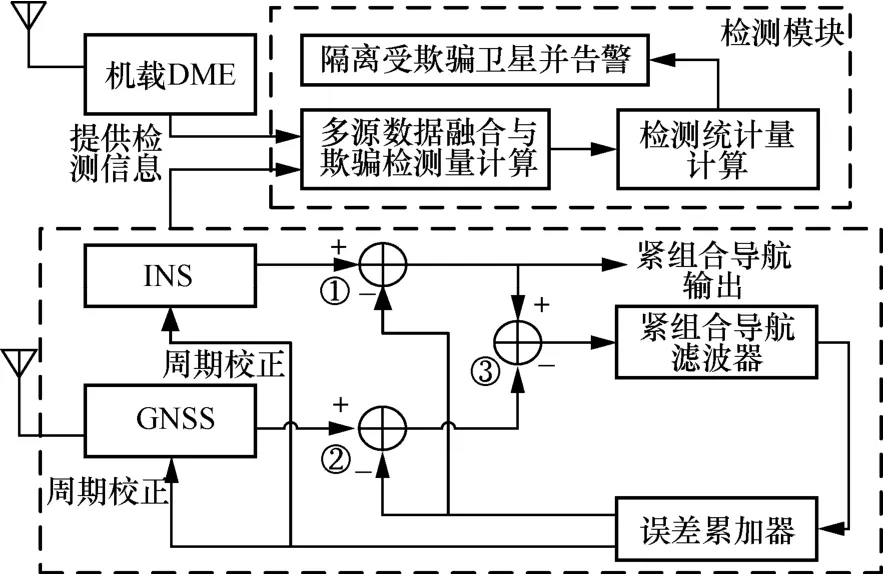
图3 误差估值累加开环校正欺骗检测系统结构

3.2 欺骗式干扰检测方法

传统的基于INS/GNSS紧组合导航的欺骗式干扰检测方法以组合导航滤波器新息构建欺骗检测统计量。新息为滤波器实际测量向量与一步预测向量的差值。当GNSS受到欺骗时，实际测量误差会改变新息序列统计特性，由零均值高斯分布改变为非零均值高斯分布。不同的欺骗式干扰检测方法的区别在于如何利用统计特性的这一变化特点。下面对传统新息序列卡方欺骗检测方法、SPRT欺骗检测方法和自适应SPRT欺骗检测方法等欺骗式干扰检测方法进行简要分析。

传统新息序列卡方欺骗检测方法以累加的历史时刻到当前时刻的新息序列卡方构建检测统计量，可以判断GNSS是否受到欺骗，但无法识别具体哪路卫星信号受到欺骗，且对诱导式欺骗的检测性能差。一般SPRT欺骗检测方法以历史时刻到当前时刻新息序列的对数似然比构建检测统计量，相对提高了对诱导式欺骗的检测性能，但由于组合导航的误差跟踪作用，该方法存在较大的检测时延。为了提高诱导式欺骗的检测性能，文献[10]改进了一般SPRT欺骗检测方法，进一步结合机载多传感器导航体制优势，利用DME的导航数据以及闭环校正紧组合导航提供的GNSS、INS导航数据构建自适应SPRT欺骗检测方法的欺骗检测统计量，加快了欺骗检测速度。

下面结合文献[10]的检测思路，简要介绍基于SPRT欺骗检测方法和自适应SPRT欺骗检测方法的检测步骤。

首先，由GNSS、INS和DME的导航数据构建完整的量测方程：

其中，y为量测向量，由卫星伪距差量测值和DME斜距差量测值构成；x为状态向量，由载体位置误差和GNSS接收机时钟误差的等效距离、DME询问器和应答器的总时间误差的等效距离构成；ε为测量噪声向量；W为归一化噪声标准差向量。

其中，G为量测矩阵：

其中，lGNSS,j、 mGNSS,j、nGNSS,j为载体与第j颗可见卫星几何连线的三维方向余弦，lDME,m、mDME,m、 nDME,m为载体与第m个DME导航台几何连线的三维方向余弦。

其次，对式（8）应用最小二乘法[15]，得到所有可见卫星的欺骗检测量：

最后，基于二元假设检验理论[13]，以式（10）得到的第j颗可见卫星欺骗检测量为输入，作为SPRT欺骗检测方法当前时刻的观测样本 ,k jf，此时，一般SPRT欺骗检测方法的欺骗检测统计量可由式（11）计算：

根据Bayes参数估计理论[16]，为改进一般SPRT欺骗检测方法的检测速度，计算一般SPRT欺骗检测方法的欺骗检测统计量的自适应补偿值 ,k jζ：

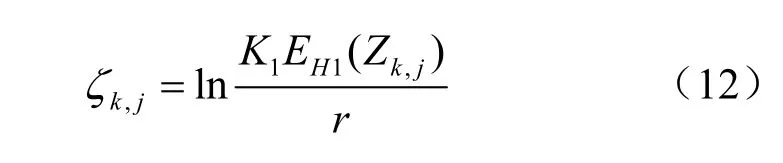
其中，比值r/K1表示对欺骗干扰施加欺骗量的敏感程度， EH1( Zk,j)为第j颗可见卫星受欺骗时对数似然比 ,k jZ的期望值。

在各个采样时刻，由式（12）补偿式（11）得到自适应SPRT欺骗检测方法的欺骗检测统计量：

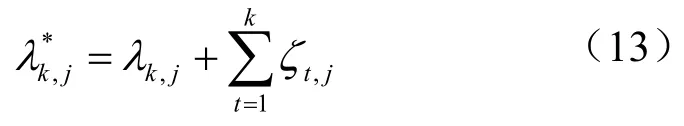
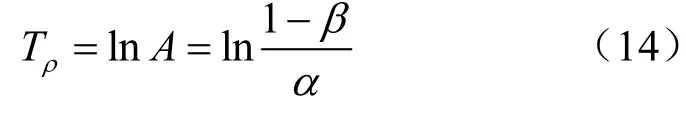
3.3 开环校正结构下欺骗检测量分析

本文方法在文献[10]中自适应SPRT欺骗式干扰检测方法的基础上引入周期校正的误差估值累加开环校正结构。利用本文开环校正紧组合导航系统输出的GNSS和INS导航信息重构由式（10）给出的欺骗检测量，解决文献[10]中闭环校正结构下INS因滤波更新校正被欺骗“污染”的问题，理论分析如下。

重构欺骗检测量即重新计算矩阵G和列向量y。由于诱导式欺骗的开始时间未知，在计算矩阵G和列向量y中包含的三维方向余弦和伪距差量测值时，所需要的INS和GNSS导航数据会根据周期校正的误差估值累加开环校正情况的变化而变化。具体计算欺骗检测量所需要的INS和GNSS导航数据来源可根据欺骗式干扰检测是否在同一个校正周期内完成分两种情况。

（1）欺骗式干扰检测在同一个校正周期内完成，INS未经过周期校正。

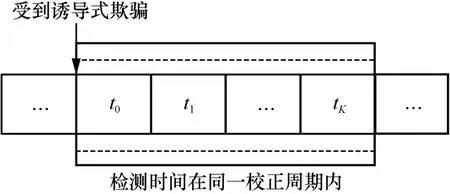
图4 欺骗式干扰检测在同一个校正周期内完成示意图

欺骗式干扰检测在同一个校正周期内完成示意图如图4所示，每个滤波时刻t0,t1,t2,…,tK-1,tK的GNSS输出的伪距测量值为ρGNSS,i(i= 0,1,2,…, K - 1,K)。状态变量中每个滤波时刻GNSS接收机钟差造成的等效距离误差表示为clk,ib，每个滤波时刻GNSS接收机时钟频率漂移造成的等效距离率误差表示为clk,id。 设 tq(t0＜tq≤ tK)时刻INS输出的北东地导航坐标系下的纯惯性位置经坐标变换到地心地固坐标系为 (xI,q,yI,q,zI,q)，设tq时刻星历提供的第j颗卫星位置为 ( xSat,j,q, ySat,j,q, zSat,j,q)(j = 1,2,…,n)，那么tq时刻载体与卫星的三维方向余弦为： 设所选的两个DME导航台位置为

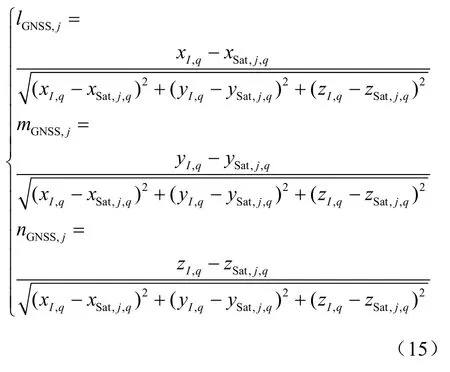
( xDME,m, yDME,m, zDME,m)(m = 1,2)，那么tq时刻载体与

DME导航台的三维方向余弦为：

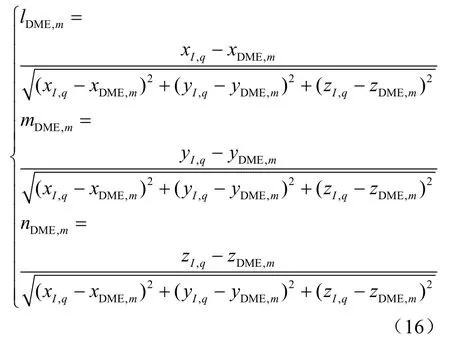
列向量y由卫星伪距差量测值和DME斜距差量测值构成。设tq时刻GNSS输出的第j颗可见星的伪距测量值为ρSat,j,q，载体和第j颗可见星的伪距差量测值 δρGNSS,j等于GNSS伪距测量值和INS等效伪距之差，则tq时刻GNSS伪距差量测值 δρGNSS,j为：

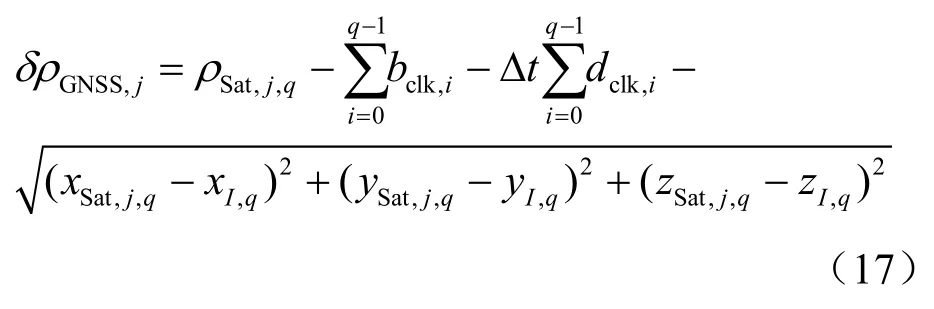
tq时刻，载体和第m个DME导航台的DME斜距差量测值 δρDME,m( m= 1,2)等于tq时刻DME斜距测量值dDME,m,q和INS等效伪距之差：

利用式（15）～式（18）可得到欺骗式干扰检测在INS未经过周期校正情况下的矩阵G和列向量y，再根据式（10）计算INS未经过周期校正情况下重构的欺骗检测量在这种情况下，相较于文献[10]中闭环校正结构提供的被欺骗“污染”的INS参数，误差估值累加开环校正结构在校正周期内提供的INS参数为不受欺骗“污染”的纯惯性导航参数，可以增加欺骗检测量包含的欺骗信息。

（2）欺骗式干扰检测不在同一个校正周期内完成，INS经过周期校正。

欺骗式干扰检测不在同一个校正周期内完成示意图如图5所示，INS经过周期校正之前的滤波时刻表示为INS经过周期校正之后滤波时刻表示为

图5 欺骗式干扰检测不在同一个校正周期内完成示意图

设受到诱导式欺骗的时刻为tsp(tsp＜tK)，在spt到Kt时刻，矩阵G和列向量y的计算方法与INS未经过周期校正情况下的计算方法相同。在tK时刻之后，欺骗检测量的计算需要考虑INS经过了周期校正，将INS被累加的误差估值周期校正内部参数后的纯惯性位置代入式（15）、式（16）和式（18）中，就可得到时刻矩阵G中包含的三维方向余弦和列向量y中包含的DME伪距差量测值。而由于GNSS在tK时刻与INS一起经过周期校正，tK时刻误差累加器已置零，故列向量y中包含的GNSS伪距差量测值的表达式与式（17）不同，其在qt′时刻为：

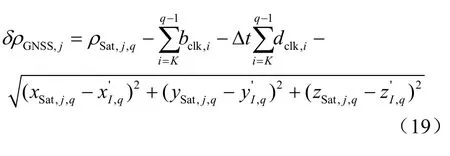
重新计算矩阵G和列向量y后，再根据式（10）计算INS经过周期校正情况下重构的欺骗检测量在INS未经过周期校正之前，INS参数仍为纯惯性导航参数。当INS经过周期校正时，欺骗检测量会突然减小，但仍然会随着欺骗量的增大而快速增大以满足欺骗检测告警时间要求。

基于以上理论分析，在检测模块中，由周期校正的误差估值累加开环校正紧组合导航系统提供INS和GNSS导航参数，重新计算矩阵G和列向量y，得到重构的欺骗检测量，然后利用式（11）～式（14）计算自适应SPRT欺骗检测方法的欺骗检测统计量进行欺骗式干扰检测。由INS是否经过周期校正的两种情况可以得出，在周期校正的误差估值累加开环校正结构下进行欺骗式干扰检测，充分利用了欺骗信息，可以缩短欺骗检测时延，提高欺骗检测速度。

4 仿真结果分析

4.1 实验设置

模拟飞机巡航阶段，验证本文所提周期校正的误差估值累加开环校正结构的紧组合导航与闭环校正结构的紧组合导航的等效性，以及在提升欺骗检测效果方面的有效性。设置两组仿真实验，仿真实验1验证两种校正结构下的紧组合导航误差；仿真实验2模拟“最坏”情形下的诱导式欺骗策略。对比两种校正结构下传统的新息序列卡方欺骗检测方法、一般SPRT欺骗检测方法以及自适应SPRT欺骗检测方法，并进行蒙特卡洛仿真，统计欺骗检测率，分析欺骗式干扰检测性能。

按照ICAO附件10标准规定[13]，仿真参数见表1。

表1 仿真参数

表1中，Li为飞机到第i个DME导航台的斜距，计算时利用INS载体位置与两个DME导航台位置计算相应的DME斜距估计值ˆρDME,i替代Li。

新息序列卡方欺骗检测方法的检测门限根据卡方分布分位数计算式，由给定虚警率确定，随着欺骗检测时间的变化而变化。一般SPRT和自适应SPRT欺骗检测方法的检测门限根据检测判决域的划分由虚警率与漏警率确定，根据表1中给定的虚警率和漏警率，通过式（14）计算可得欺骗检测门限为常值Tρ=11.511 9。

参照ICAO附件10对机载设备巡航阶段30 s告警时间的要求，将加入欺骗式干扰后的30 s内欺骗检测统计量超过检测门限记为一次成功检测。在告警时间要求下的欺骗检测率P2的可综合反映欺骗检测速度和检测精度，表征欺骗检测性能。

4.2 实验结果分析

（1）仿真实验1

验证本文所提周期校正的误差估值累加开环校正结构的等效性。

根据表1，在不存在欺骗的条件下，得到INS/GNSS紧组合在闭环校正结构和本文所提周期校正的误差估值累加开环校正结构下北、东、地方向的位置、速度误差。两种校正结构下紧组合导航误差如图6所示。

图6中，在两种不同的校正结构下，INS/GNSS紧组合导航系统的位置误差和速度误差基本一致，但不完全重合，这是由系统随机噪声的存在导致的。根据《机载惯性—GNSS组合导航系统通用规范》（GJB5298-2004）要求，组合导航状态的水平位置误差和垂直位置误差应不大于100 m和156 m，水平速度误差和垂直速度误差应不大于0.8 m/s和1.0 m/s。可以认为3个方向的位置、速度误差都在符合预期的误差范围内。这表明在工程应用中，这两种校正结构的替换不会导致INS/GNSS紧组合导航系统的导航性能改变，验证了本文所提误差估值累加开环校正结构与闭环校正结构的等效性。

（2）仿真实验2

验证周期校正的误差估值累加开环校正结构相对于闭环校正结构在诱导式欺骗下的有效性。

针对“最坏”情形下的诱导式欺骗策略，其ωΔρ=0，伪距诱导速率 a≠0，恒伪距欺骗量b=0。从200 s开始，通过对单颗卫星施加伪距诱导速率不同的诱导式欺骗，对比3种方法。

误差估值累加开环校正结构下3种方法的欺骗检测统计量如图7所示。

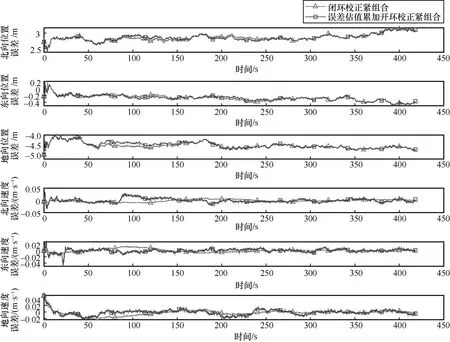
图6 两种校正结构下紧组合导航误差

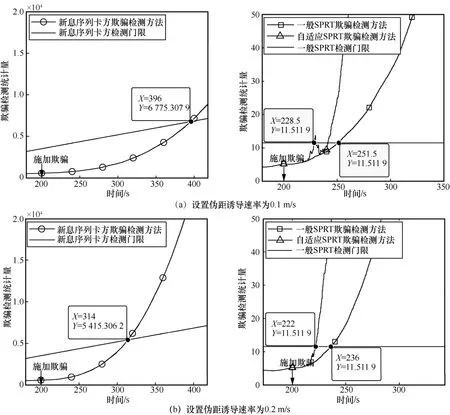
图7 误差估值累加开环校正结构下3种方法的欺骗检测统计量

在图7（a）中，误差估值累加开环校正结构下对于伪距诱导速率为0.1 m/s的“最坏”情形下的诱导式欺骗，自适应SPRT欺骗检测方法的欺骗检测统计量在加入欺骗后的28.5 s检测出欺骗的存在，但随后又下降。这是由于设置欺骗开始时刻和周期校正时刻重合，所以自适应SPRT欺骗检测方法的欺骗检测统计量加入欺骗后的第30 s会被累加的误差估值校正，导致INS被“污染”，致使欺骗检测统计量下降。而在周期校正后，随着伪距欺骗量的持续增大，欺骗检测统计量继续增加，这种现象只有在伪距诱导速率微小时才明显。在相同时间施加欺骗的条件下，将欺骗检测统计量超出检测门限的时间减去施加欺骗的时间得到3种方法的欺骗检测时间，周期校正的误差估值累加开环校正结构下对比3种方法的欺骗检测时间见表2。

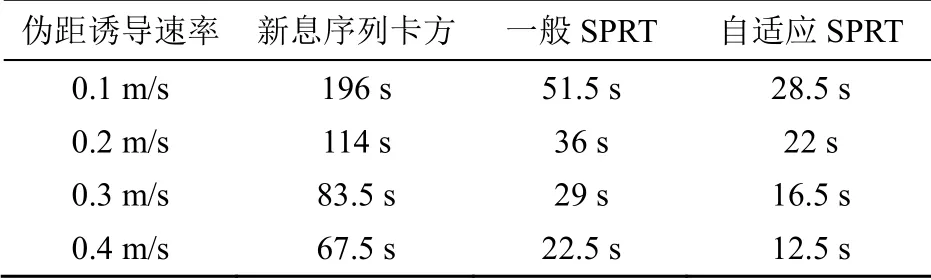
表2 周期校正的误差估值累加开环校正结构下 3种方法的欺骗检测时间

闭环校正结构下3种方法的欺骗检测统计量如图8所示。

从图8可以看出，在第200 s刚加入欺骗之后，自适应SPRT欺骗检测方法的欺骗检测统计量存在小幅波动，这是由伪距测量噪声的存在造成的，自适应SPRT欺骗检测方法中的补偿值根据当前检测量大小自适应改变，不会因噪声的存在形成较大补偿，进而造成欺骗检测统计量超过门限。

闭环校正结构下对比3种方法的欺骗检测时间见表3。

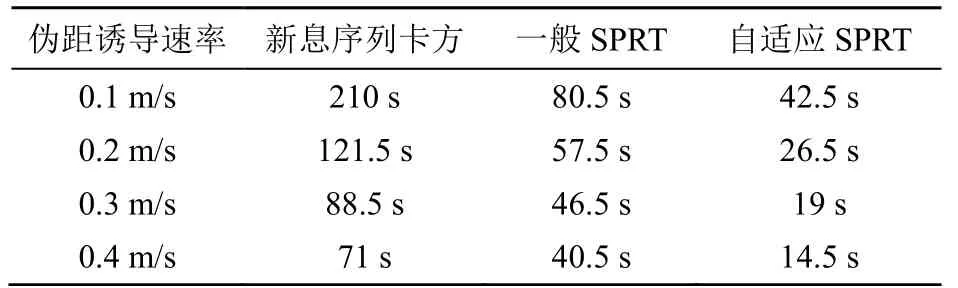
表3 闭环校正结构下3种方法的欺骗检测时间

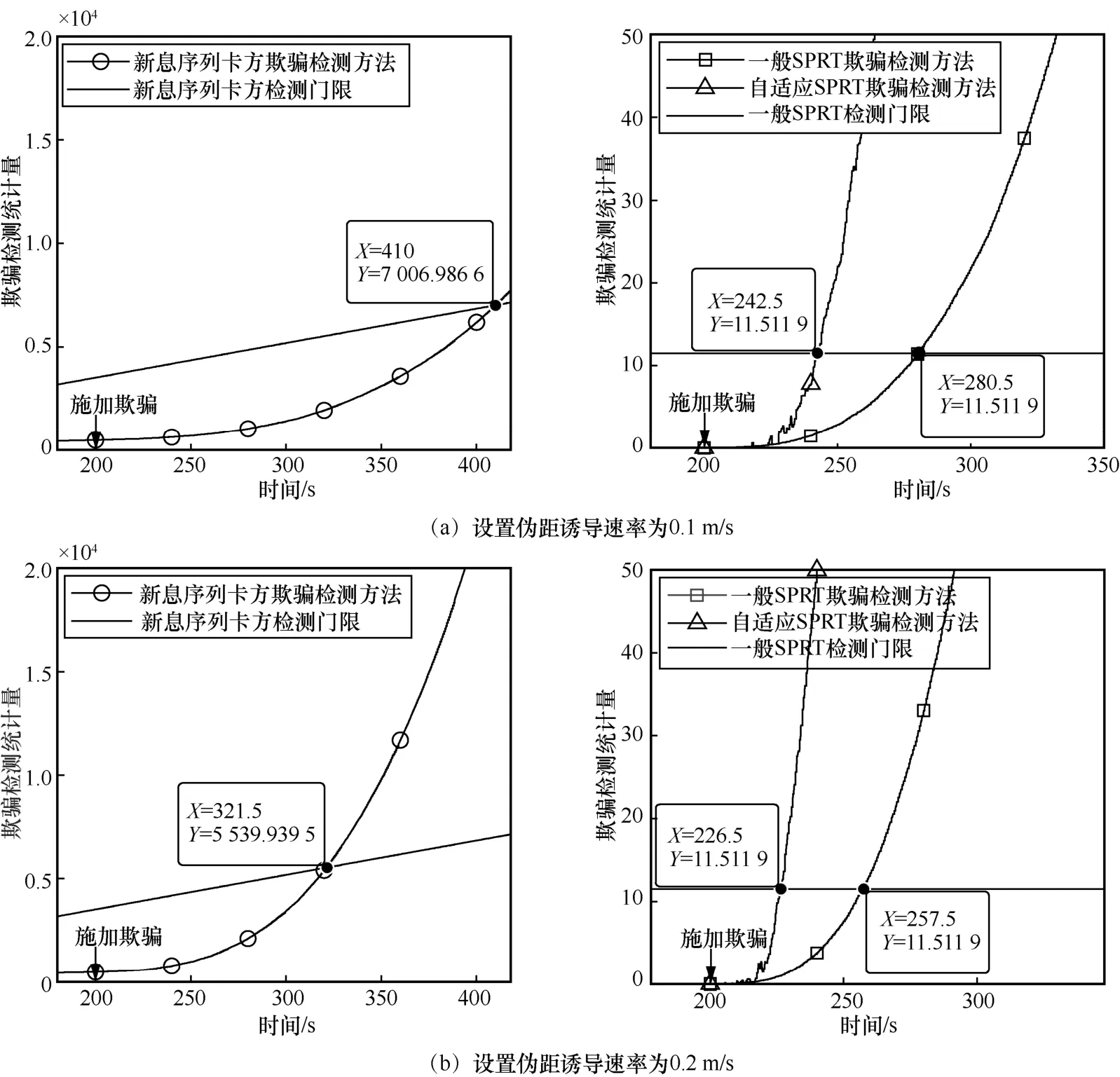
图8 闭环校正结构下3种方法的欺骗检测统计量

对比表2和表3可得，在“最坏”情形下，误差估值累加开环校正紧组合下3种方法的欺骗检测时间均要小于闭环校正紧组合。新息序列卡方欺骗检测方法检测时间的提升在6%以内，一般SPRT欺骗检测方法的检测时间的提升在37%左右，自适应SPRT欺骗检测方法检测时间的提升在20%左右。这表明在“最坏”情形下，误差估值累加开环校正结构对一般SPRT和自适应SPRT欺骗检测方法在欺骗检测时间方面的性能提升更显著，能有效提高自适应SPRT欺骗检测方法在“最坏”情形下对微小变伪距欺骗量的检测敏感度。

对单颗卫星施加伪距诱导速率不同的诱导式欺骗，进一步验证闭环校正结构和开环校正结构下新息序列卡方欺骗检测方法、一般SPRT欺骗检测方法以及自适应SPRT欺骗检测方法的欺骗检测率。闭环校正结构和开环校正结构下3种方法的欺骗检测率变化曲线如图9所示。

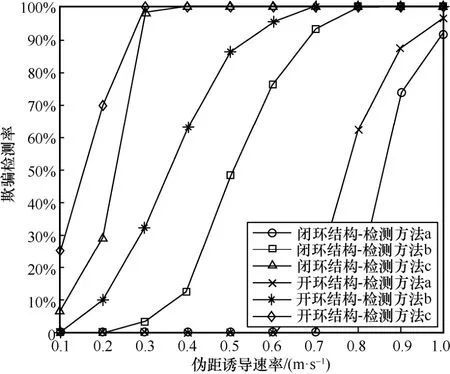
图9 闭环校正结构和开环校正结构下3种方法的欺骗检测率变化曲线

图9中，检测方法a指新息序列卡方欺骗检测方法，检测方法b指一般SPRT欺骗检测方法，检测方法c指自适应SPRT欺骗检测方法。由图9可得，针对“最坏”情形下的诱导式欺骗，在闭环校正结构下，当伪距诱导速率为0.4 m/s时，自适应SPRT欺骗检测方法的欺骗检测率收敛于100%。而在开环校正结构下，当伪距诱导速率为0.3 m/s时，自适应SPRT欺骗检测方法的欺骗检测率收敛于100%。通过对比，在相同的伪距诱导速率下，3种方法在误差累加开环校正紧组合系统中的欺骗检测率要优于在闭环校正紧组合中的欺骗检测率。这表明周期校正的误差估值累加开环校正结构能有效地对“最坏”情形下的诱导式欺骗干扰进行检测。

5 结束语

本文提出了一种周期校正的误差估值累加开环校正结构下的诱导式欺骗干扰检测方法，实现了对“最坏”情形下的诱导式欺骗干扰的检测。周期校正的误差估值累加开环校正结构可以在保证组合导航滤波器不发散的条件下提高欺骗检测算法的检测性能。本文通过理论分析和仿真实验，验证了周期校正的误差估值累加开环校正结构下和闭环校正结构下紧组合导航精度的等效性，以及周期校正的误差估值累加开环校正结构下自适应SPRT欺骗检测方法对“最坏”情形下的诱导式欺骗干扰检测的有效性。本文周期校正的误差估值累加开环校正结构可进一步应用于现有的机载导航体制中，为其提供不受外部因素影响的冗余导航信息。