基于多通道的边学习图卷积网络

2022-10-09杨帅王瑞琴马辉

电信科学 2022年9期

杨帅，王瑞琴，马辉

（湖州师范学院信息工程学院，浙江湖州 313000）

0 引言

近年来，神经网络方法在各种顶级会议与期刊上成为最热门的机器学习技术之一。例如，卷积神经网络（convolutional neural network，CNN）[1]在图像识别领域、循环神经网络（recurrent neural network，RNN）在自然语言处理领域等方面，解决实际需求的问题时以优异的性能受到研究人员的青睐。在现实世界中许多问题可以直接用图代替传统的表格、图像或时间序列建模，并且比传统模型更加直观高效。一般来说，图由节点和边组成，在现实生活中真实存在的部分可以作为节点，其间存在的联系或互动作为边。例如，路上的公交车站可以作为节点，公交车的运行路线可以作为边。对于节点，一般可以收集其信息建模为特征向量；对于路线，可以简化为节点间的直线边进行建模。由于图一般具有复杂的结构信息，图学习的一个挑战就是找到一个行之有效的方法在众多信息中学习一个高效的模型。这几年来，研究者们已经开发了数种针对图学习的神经网络模型，相比传统的神经网络模型，其性能更优异，应用也更广泛。受图傅里叶变换的启发，Defferrar2等[2]将卷积神经网络中的卷积操作为原型提出了一种图卷积运算，Kipf等[3]使用重新归一化的一阶邻接矩阵逼近多项式，以获得图节点分类任务的可比较结果，这些图卷积网络（graph convolutional network，GCN）[2-3]是结合图节点特征和图拓扑结构信息进行预测的。Veličković等[4]将注意力机制引入图学习，提出了图注意力网络（graph attention network，GAT）。

目前，许多图神经网络模型存在的一个问题是未能充分利用图中的边特征。在图卷积神经网络中，图被简化为无边属性的连通图，在图注意网络中同样只需要使用节点间是否连通的特性。然而，实际上图的边通常拥有丰富的特征，如强度、类型、各种离散数值等多维变量。合理地利用边特征可能会帮助许多图学习方法获得更高的精度。图神经网络的另一个问题就是每个神经层是根据作为输入给出的原始邻接矩阵聚合节点特征，但是原始的图网络有可能存在噪声问题，这将限制信息聚合与预测任务的有效性。本文在标准GCN的基础上以更合理的方式利用边特征并优化噪声问题，提出边学习图卷积网络（e2ge- learning graph convolution network，EGCN）。本文在几个引文网络数据集和分子数据集上进行了实验。通过利用多通道学习边特征，本文的方法与其他的最新方法相比，获得了不错的结果。实验结果表明，边特征对图学习具有重要帮助，并证明EGCN可以有效地学习边特征。总之，本文的特点包括两点：提出了针对数据中存在的噪声的优化方法，该方法通过多层感知机（multilayer perceptron，MLP）计算节点间的类相似度，忽略部分类相似度值较低的噪声边的影响，从而提升模型性能；提出多通道边特征学习的方法，对图中边的每一种属性进行编码，使模型在训练中更合理地学习边的不同属性的隐藏特征。

1 相关工作

图学习的一个关键问题是图数据的复杂非欧结构。为了解决这一问题，传统的机器学习方法用图表统计、核函数或其他手动制作的特征提取邻域局部结构特征。这些方法缺乏灵活性，且手动设计合理的功能非常耗时，需要大量的实验才能将其推广到不同的任务或数据集中。图表示学习尝试使用数据导向的方法将图或图节点嵌入低维向量空间，较为流行的一类为基于矩阵分解的嵌入方法，如拉普拉斯特征映射、图分解和高阶邻近保持嵌入（high-or2er proximity preserve2 embe22ing，HOPE）；另一类方法侧重于使用基于节点相似性度量的随机游走，如DeepBalk、no2e2vec和大规模信息网络嵌入（large-scale information network embe22ing，LINE）。基于矩阵分解和基于随机游走的图学习方法均存在一定的局限性。例如，映射到低维向量空间的嵌入函数是过于简单的线性函数，可能无法捕捉复杂的信息，而且它们通常不包含节点特性；它们需要从邻域聚合信息，所以需要对整个图的结构进行训练。

最近，随着深度学习的发展，图学习中的部分问题有所解决。基于神经网络的深度学习可以表示复杂的映射函数，并通过梯度下降方法进行有效优化。随着CNN在图像识别方面的成功，人们自然而然地想将卷积应用于图形学习中。在文献[5]中，卷积运算是在图拉普拉斯变换的谱空间中定义的。Defferrar2等[2]提出利用图拉普拉斯算子的切比雪夫展开式近似滤波器，从而产生空间域局部化的滤波器，同时避免了计算特征向量的拉普拉斯算子。Veličković等[4]在图学习中引入了注意机制，提出了GAT。但GAT与GCN仍重点关注节点特征，未能充分考虑节点间边的多维信息特征，仅使用了边的连通性，同时他们的模型没有考虑任务中部分节点的邻居节点有误导影响，没有考虑噪声的局限性。

为了有效利用图上的边特征，边增强图神经网络（e2ge enhance2 graph neural network，EGNN）[6]对边特征使用双重随机归一化以及跨网络自适应方法以学习边特征，并且在GCN与GAT的基础上提出了EGNN（C）与EGNN（A）的改进模型。Chen等[7]则通过提取边与节点的互信息（mutual information），提出边信息最大化图神经网络（e2ge information maximize2 graph neural network，EIGNN）。Gilmer等[8]研究近年来的众多图学习模型的共性后，提出了消息传递神经网络（message passing neural network，MPNN），图神经网络的本质是特征聚合，即节点根据周围邻居节点更新自身特征信息，这个方法即消息传递。上述图神经网络将部分边信息引入图学习，但仍存在未充分利用边的多维信息和原始节点间可能存在噪声影响的局限性。

2 多通道图卷积神经网络的结构

传统的GNN有许多变体，如GCN[3]、GAT[4]、Graphs AGE[9]等。这些神经网络模型侧重于学习节点状态，可以为邻居分配权重，但不能处理各种边特征。其中，通用的邻居节点聚合方案为：

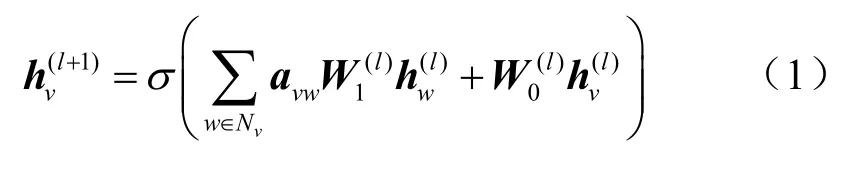
其中，l表示第l层神经网络层，σ为非线性激活函数；avw是一个标准化常数或学习注意系数；h是一个将节点特征从输入空间映射到输出空间的变换，Wl是一个Fl×Fl+1的可学习权重矩阵。这些聚合方法尚不能满足处理边特征的需求。例如，对于分子分析的任务来说，原子键上的属性对于分子属性具有决定性影响，但目前的图神经网络大多是针对单维边属性设计的，且不适合分子分析这种单个图比较小、总体上图的数量多的任务。

在传统图卷积神经网络的基础上，本文的多通道边学习图卷积网络模型总体结构如图1所示。

图1 多通道边学习图卷积网络模型总体结构

设一个图G=(V, E)，G表示有N个节点的图，其中V是一组N个数据的节点表示，E是一组N个数据的边表示。图1中的节点编码为特征矩阵X∈RN×f，f表示一个节点的维度，X0是第一层神经网络的输入，Ek表示通道k中的边矩阵。在图1中，上标l表示第l层的输出。首先，用MLP层对数据进行预处理，经过预处理后获得更适合本文模型需要的节点集X0与边集E0并将其输入下一步的神经网络层。在信息聚合层，X0和E0表示神经网络的输入。在第一层聚合层将边特征E0应用于X0，经过聚合邻域产生一个N×F1的新节点特征矩阵X1。经过调整的E1作为边特征送到下一层。这个步骤在以后的每一层都重复。节点特征XL可被认为是图节点在Fl维空间中的嵌入。对于节点分类问题，将softmax函数应用于最后一维的每个节点嵌入向量XL。对于全图预测（分类或回归）问题，将池化层应用于XL的第一维，从而将特征矩阵简化为整个图的单个向量嵌入。然后将全连接层应用于图向量，其输出可用于预测回归，也可用于分类。

2.1 去噪处理

现有图网络的初始邻接矩阵可能有噪声且不是最优的，这将影响邻域聚合操作的有效性。例如，引文网络中机器学习论文有时引用数学论文或其他理论论文，然而，数学论文可能很少引用机器学习论文。在此之前已有类似的工作，例如，文献[10]使用标签传播和单个训练过的图神经网络模型扩大图神经网络的训练集，文献[11]采用DeepCluster[12]等无监督学习技术帮助图神经网络的自训练，文献[10]和文献[11]可被看作是图神经网络自训练或协同训练的特定算法，文献[13]使用正则化项对每个节点提供新的监督信号进行训练。

节点间的类相关度可以通过直接使用标签加节点数据进行计算获得，但是在稀疏分割条件下，只有小部分节点和标签可用，很难直接从节点和标签计算其类相关度，所以本文使用多层感知机从节点特征中学习获得类相关度。具体来说，首先用多层感知机从原始节点属性中提取类感知信息，多层感知机的第l层的定义为：

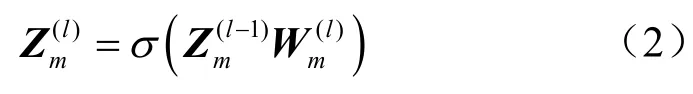
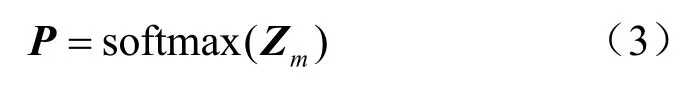
总的来说，本步骤基本思想为基于阈值的节点间类相似度的边筛选方法，基于MLP的分类标签生成候选边集。在训练过程中计算节点间的类相似度，将类相似度值低于阈值的节点对的边划入低类相关度集合，选择集合中的一定比例的最低值的边置为0，即经过算法处理可得分配矩阵，该矩阵在网络中的作用为按比例删除假定为噪声的边。为了不过度破坏数据集原有的结构以致影响任务的精度，实验中对于节点低相关性的边进行保守删除，过高的删除比例虽然会获得更高的准度，但会出现训练严重过拟合、精度不高等问题。

2.2 基于多通道边学习的图卷积网络

通常实际数据中图的边上包含有关图的重要信息。例如，在引文网络中，引用关系应该是有方向的，对于节点分类任务来说，论文的引用方向可能有十分重要的作用，因此在建模引文网络数据集时，将论文的引用方向作为一组边特征编码为一个通道；在分子性质分析任务中，对分子建模时，由于其性质十分复杂，不能简单地将其视为无属性连通图。本文根据图数据天然存在的属性将边编码为多维矩阵，边的每一个属性将对应一个通道，让模型在各通道中根据不同的神经网络参数学习节点特征与边特征。在引文网络数据集中将论文的引用方向和引用次数分解为双通道进行建模，将分子数据利用不同的边属性分解为5个通道建模。图的边特征作为输入进入卷积层将被转化为边约束，卷积层l中的图在基于边约束的条件下转换为约束图信号，这个图信号由边约束矩阵{A1,A2,…,Ak}组成。图卷积聚合来自每个通道的所有一阶邻居的节点信息。在第l层中，约束图信号的图卷积式为：

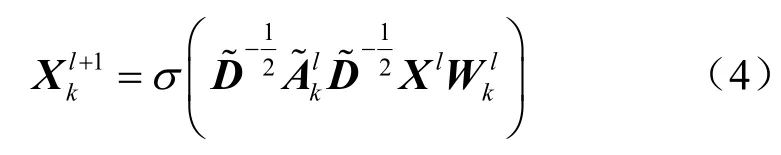
图卷积的一个重要工具是图拉普拉斯矩阵[3]。经过证明，归一化的图拉普拉斯矩阵定义为

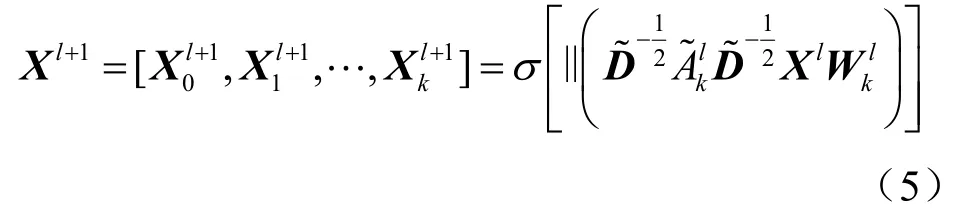
算法1多通道的边学习图卷积算法

输入通道k；模型f (·)；节点张量X；边张量E；邻接矩阵A

可学习参数：权重W，权重w

多通道卷积方法

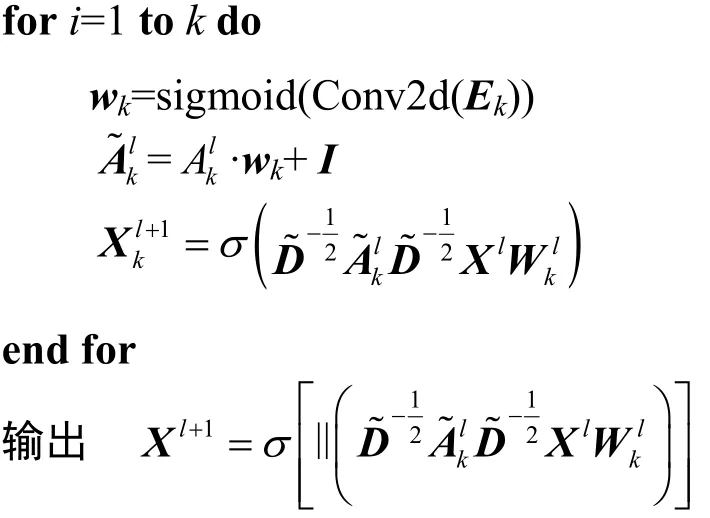
总之，本文的工作是基于一阶近似的切比雪夫（Chebyshev）卷积，在此基础上使用多通道学习方法对图卷积进行多次使用。多通道机制在模型学习过程中会产生一组边权值wk，这些参数提供了比传统图卷积网络更具表现力的网络模型，图卷积网络可以学习节点之间多种边类型，根据不同通道的可学习参数，让模型学习不同边属性的特征。

2.3 可微分池化

本文模型使用了可微分池化（Diffpool）[14]以层级化学习图表示。可微分池化设计了一个图池化神经网络来生成节点的赋值矩阵S：

softmax函数的输入是特征矩阵Xl和邻接矩阵A，是第l层的传统图卷积网络[3]。在可微分池化层的第一层nl= n，由于加入了多通道学习方法，第一个可微分池化层的输入是，然后使用得到新的聚类邻接矩阵Xl+1和聚类节点的特征矩阵Al+1，如式（7）、式（8）所示。

最后的输出是图表示X∈R1×fG，fG表示图的维数。Diffpool定义了新的层级化池化层以抽取图的信息，通过学习赋值矩阵将不同的节点分配到不同的聚类中，结合正则化的边预测来共同优化学习卷积参数，从而学习到更丰富的层级化网络信息。

2.4复杂度分析

与传统的卷积神经网络不同，由于不同的节点与边的复杂性不同，图卷积的成本是不稳定的，无法准确给出每一步计算的时间复杂度，在计算机中数据的加减运算的成本较低，故训练算法的时间复杂度可以通过乘法运算的次数进行推算。GCN、GAT与EGCN的时间复杂度与内存复杂度对比见表1。

在表1中，n是所有节点的数量，m是所有边的数量，K是网络层数，c是通道数量，节点隐含特征维数为d。传统的GCN[3]的时间复杂度为O(Kmd+Knd2)，GAT较GCN的计算量更少，但是需要处理的数据规模是相同的，而本文同样使用传统GCN的基于一阶近似的切比雪夫卷积，所以增加的时间复杂度与计算复杂度为增加的通道数量。

3 实验结果

本文所有的算法与实验都基于Python 3.7平台上的torch-1.6.0实现。在所有的实验中，模型都用Intel core i5-10500处理器进行处理。实验的任务包括验证本文方法对几种基础方法的改进。由于引文网络数据集需要使用边特征来建模，因此使用了Cora和Citeseer的原始版本。分子数据集使用了Tox21、Freesolv、Lipophilicity和eSOL数据集。节点特征和边特征是使用RDKit提取的，RDKit是一个开源的化学信息学软件包。RDKit将SMILES字符串转换为“mol”格式，其中包含用于构建分子图的分子结构信息。

3.1 数据集

为了测试本文提出EGCN的有效性，将其应用于多种常见的数据集。本节测试了两个节点分类任务引文网络数据集——Cora、Citeseer；一个全图分类任务的分子分析数据集，Tox21；3个预测分子性质的分子分析数据集，Lipophilicity、Freesolv和eSOL。引文网络中的Cora与Citeseer均用论文中关键字是否出现以二进制指标表示节点特征，根据论文的引用方向关系编码为多个离散值的边特征矩阵。Tox21的原始数据来自21世纪的毒理学研究计划，它包含7 831个环境化合物和药物，以及12个标签的生物学结果，是全图分类任务。回归任务有3个数据集：Freesolv是一个含有642个水中小中性分子的水合自由能的数据库；Lipophilicity（Lipo）由ChEMBL数据库整理，包含4 200个化合物；eSOL提供了1 128种化合物的水溶性数据。各数据集的基础统计数据见表2。分子数据集均从MoleculeNet[15]下载。实验中忽略了结构图没有边的SMILES样本。

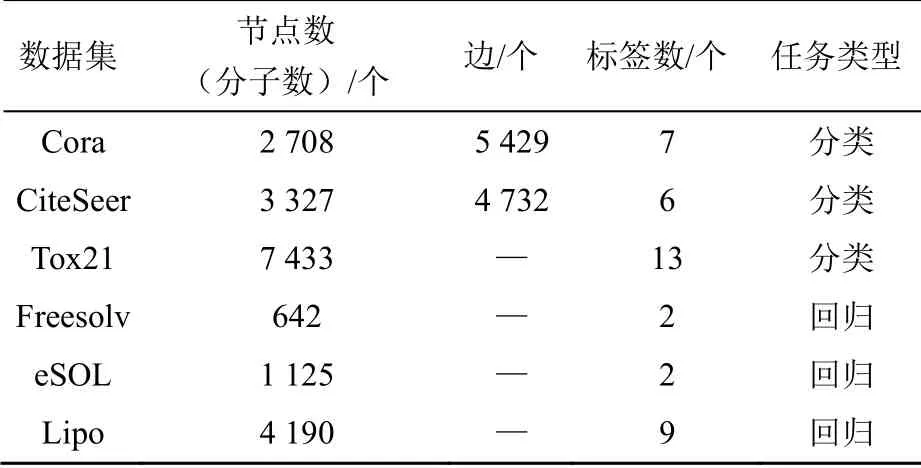
表2 各数据集的基础统计数据

3.2 评价指标

对于分类任务，Cora与Citeseer数据集的任务为节点分类任务，评价指标为准确率，由预测标签和实际标签计算得来。Tox21数据集的任务为分子分类，即全图分类，采用ROC曲线下面积（area un2er curve，AUC）作为评价指标。其中，ROC曲线全称为“受试者工作特征曲线（receiver operating characteristic curve）”，它是根据分类得到的二值分类结果，以真阳性率（true positive rate，TPR）为纵坐标、假阳性率（false positive rate，FPR）为横坐标绘制，AUC值可通过对ROC曲线下各部分的面积求和而得。由定义可知AUC取值在0.5和1.0之间，越接近1.0，模型可靠性越高。

表1 GCN、GAT与EGCN的时间复杂度与内存复杂度对比

Lipo、Freesolv与eSOL数据集为回归任务，比较模型在不同数据集上的预测误差，采用均方根误差（root mean square error，RMSE）作为评价指标，由式（9）可知RMSE值由算法的预测值iy和实际值计算得来，RMSE值越小，模型性能越好。

3.3 对比算法

本文将提出的基于多通道边学习的图卷积网络与传统的图卷积网络、图注意网络等分别做了相应的对比，几种对比算法的简介如下。

（1）图卷积网络[3]使用一阶近似的切比雪夫卷积实现谱域卷积。

（2）图注意力网络[4]将注意力机制引入基于空间域，通过一阶邻居节点的不同权重的表征更新节点特征。

（3）随机森林（ran2om forest，RF）算法[15]通过训练多个决策树，生成模型，然后综合利用多个决策树进行分类。

（4）Beave[15]模型原理类似于图卷积，Beave 特征化编码了局部化学环境和分子中原子的连通性，专门用于分子分析。

（5）边增强图神经网络[6]是通过多种边处理方法以学习边信息的图神经网络。

（6）边信息最大化图神经网络[7]通过最大化边特征与消息传递通道间的互信息来学习边的多维属性。

（7）消息传递神经网络[8]是通过关注节点之间信息的传递，定义聚合函数而提出的一种通用的GNN框架。

3.4 结果分析

3.4.1 引文网络实验

对于引文网络数据集Cora和Citeseer，任务为对论文进行分类，是节点分类任务。本文将整个数据集划分为训练集、验证集和测试集，参照文献[6]将数据集分为稀疏分割（Sparse）和密集分割（Dense）两种模式，稀疏分割划分为5%训练、15%验证和80%测试的3个子集；密集分割划分为60%训练、20%验证和20%测试的3个子集。对于类相似度估计，使用一个隐藏层有512个单元和另一个隐藏层有32个单元的双层MLP。对于神经网络层，按文献[6]的参数设置，使用两层的卷积层，隐藏层设置输出维度为64，2ropout率设为0.5，对权值W进行L2正则化，权值衰减为0.000 5，并采用指数线性单元（exponential linear unit，ELU）作为隐藏层的非线性激活。在本次实验中，将标准的GCN[3]与GAT[4]作为基础对照方法，并将文献[6]中最佳性能的EGNN加入对比试验。同时，为了研究每个功能的有效性，在实验中对模型进行了消融实验，EGCN（N）表示保留图去噪方法，EGCN（M）表示保留多通道边学习方法，EGCN（MN）表示使用完整的模型。本节总共测试了6个模型在Cora和Citeseer两个数据集的两种分割方法下的表现，每个模型分别运行10次，取其精度的均值和标准差。各模型基于引文网络数据集的结果和EGCN模型在引文网络数据集上消融实验的结果分别见表3和表4，其中粗体数字表示不同模型得到的最好性能。

表3 各模型基于引文网络数据集的结果

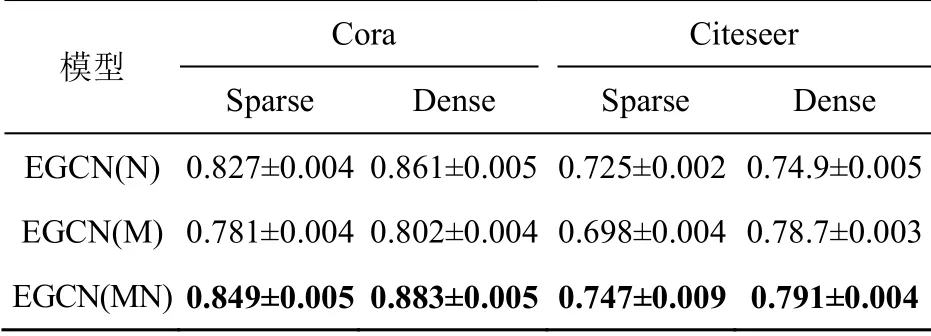
表4 EGCN模型在引文网络数据集上消融实验的结果

分析表3和表4可知，EGCN总体上比基础的GCN与GAT模型有更好的性能，保留去噪方法对分类结果的准确率提升效果明显，而保留多通道边学习方法提升较小，可能是引用网络数据集的可用边特征较少，对算法的影响有限，密集分割条件下，EGCN在Cora数据集上表现为第二优。这些结果表明EGCN模型在数据集较为简单的情况下仍能保持相当的性能。考虑到实际应用中可能存在实体标签缺失的问题，如何提高模型在稀疏分割或半监督任务下的性能是未来研究的一个方向。

3.4.2 分子分析实验

本文在4个分子数据集：Tox21、Freesolv、eSOL及Lipo上进行测试，数据集均使用RDKit将分子转换为图数据，将原子键信息编码为边特征矩阵。对于模型，本文采用两层图卷积层，每个通道的各图处理层的输出维度分别为60、100，一层微分池化层，输出维度为128，一层全连接层，输出维度为64。对于分类任务，全连接层使用sigmoi2交叉熵损失函数输出logits。回归任务的全连接层使用均方误差损失函数输出 logits。对权值W进行L2正则化，权值衰减为0.000 1，2ropout率设为0.6，采用指数线性单元作为隐含层的非线性激活。在分子分析任务中，将实验中最佳性能的EGNN[6]模型加上GCN[3]、GAT[4]、EIGNN[7]和MPNN[8]作为参照，另外也加上RF和Beave进行了测试。参照文献[6]的设置，这些数据集以80%、10%、10%的比例分为训练、验证和测试子集。上述模型每个运行5次，取评价得分的平均值和标准偏差。对于分类任务（Tox21），采用ROC曲线下方面积作为评价指标；对于回归任务（Lipo等），采用均方根误差作为评价指标；分子数据集下各神经网络的结果见表5，其中粗体数字表示不同模型得到的最好性能。

EGCN在Freesolv与eSOL分子数据集上的消融实验结果见表6，验证了多通道学习在模型中的必要性。基于分子分析数据集的EGCN中共有5个通道，分别代表分子图数据集中的

Atom Pair Type、Bon2 Or2er、Aromaticity、Conjugation和Ring Status的属性。消融实验基于Freesolv与eSOL数据集，k表示EGCN中保留的通道数量，当k=1时EGCN退化为传统GCN模型，故将GCN引入对比测试。每个EGCNk均为记录多次实验平均值加标准差，例如，EGCN4为保留4个通道，具体来说就是每次删除一个通道，运行5次，然后删除其他数个通道重复该操作，共记录25条数据，取其均值。

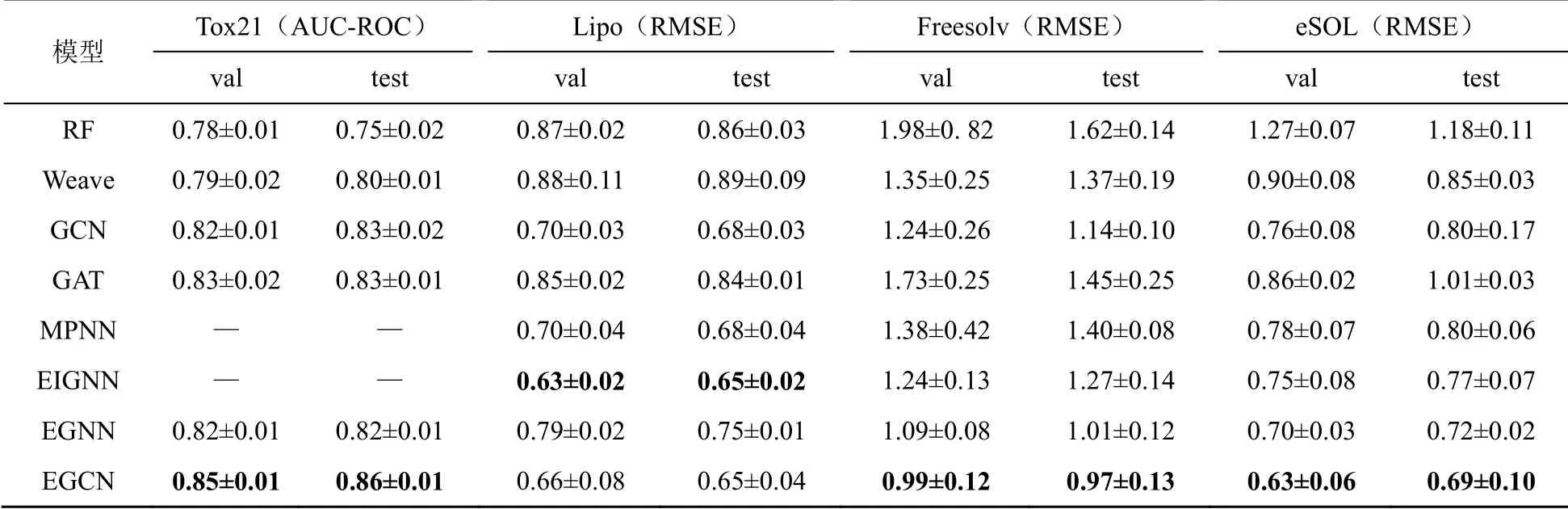
表5 分子数据集下各神经网络的结果

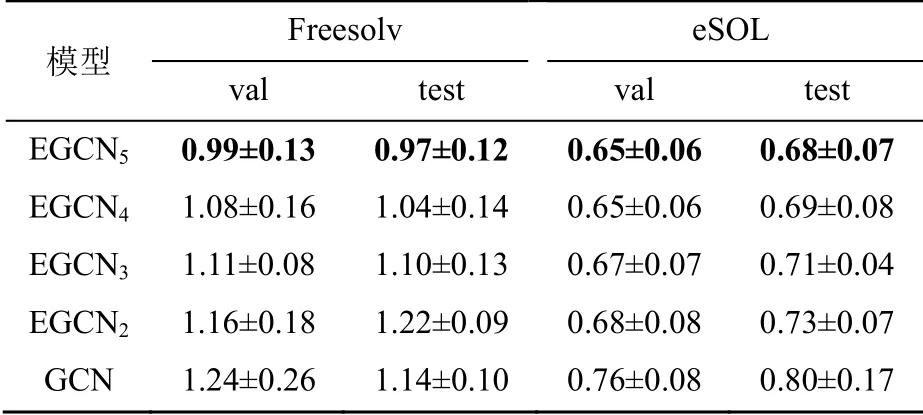
表6 EGCN在Freesolv与eSOL分子数据集上的消融实验结果

从表6中可以清楚地看到删除数个通道后的结果与原模型的实验结果，比较分析后可知通道数量增加使模型性能有明显提升。

3.5 参数敏感性分析

在去噪处理这部分，计算节点间的类相关度使用MLP从节点特征中学习获得类相关度矩阵，再将类相关度值最低的边删除，删除一定数量的噪声边后根据剩余边比例获得数据结果，EGCN在Cora数据集上基于剩余边的比例的准确率如图2所示。

图2 EGCN在Cora数据集上基于剩余边的比例的准确率

从图2可以看出，经过去噪处理后分类准确率提升明显，说明图中的部分噪声边影响明显，剔除噪声后EGCN能有效提升分类性能。被删除的边达到一定数量后，继续删除图中的噪声边虽然可以获得略高的准确率，但是提升幅度不明显，并且训练准确率已达100%，表明过拟合效应严重。这里可以认为进一步删除边会造成数据失真以致训练过拟合，所以选择保留96%的边作为后续实验的阈值。

在传统的CNN[1]中扩大感受野可以明显提高模型性能。图卷积神经网络在引入多通道学习后，为了探究更大的感受野对模型训练是否有增益，本节在一阶近似的切比雪夫卷积的基础上对模型进行k阶切比雪夫多项式改造。高阶邻域对于图卷积神经网络意味着更大的感受野，对于分子分析来说，单个分子作为一个小型图，对其使用高阶卷积可能并不适合。本节实验基于Cora与Citeseer数据集进行对比。这里将k的阶数设为1～4，基于Cora与Citeseer的k阶邻域对比实验结果如图3所示。

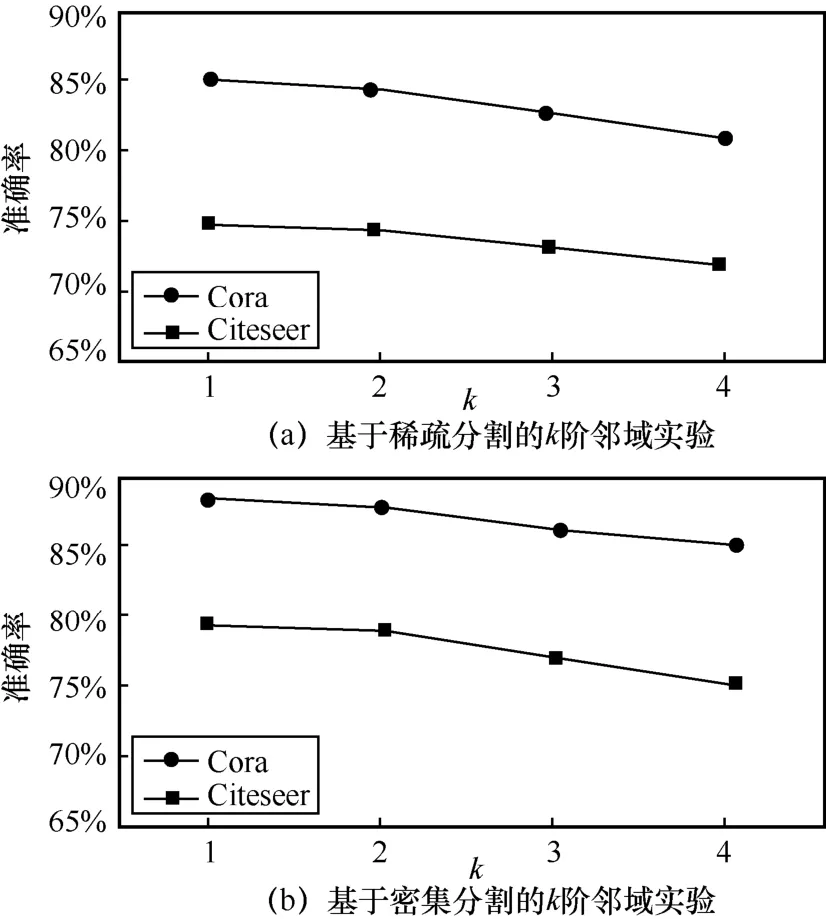
图3 基于Cora与Citeseer的k阶邻域对比实验结果

图3中，在Cora与Citeseer数据集上，与k=1相比，当k=2时准确率有略微下降，当k=3或k=4时准确率均出现明显降低。基于这些结果分析可知，对于图卷积网络，每次消息传递来自其k阶邻域，通常需要一个合适的感受野捕捉邻域信息，直接邻域足以提供卷积所需的特征信息，来自高阶邻域的大量信息会放大噪声的干扰，并对节点预测任务造成负面影响。在实验中发现，使用高阶切比雪夫卷积时会增大模型的计算量，且明显增加训练的时间，所以EGCN采用一阶近似的切比雪夫卷积。