激光陀螺捷联惯组角动态误差分析及其抑制方法

李 鹏，王慧敏

(北京航天时代激光导航技术有限责任公司，北京 100094)

0 引言

激光陀螺是基于光学Sagnac效应，通过环形谐振腔内两束相向行波频率差(拍频)敏感腔体转动角速率的光学陀螺。由于环路的非均匀性和光路的背向散射等原因，当频率差较小时，两束光的频率会被牵引至同步，陀螺仪无测量输出，这种现象称为闭锁效应。机械抖动偏频技术是目前最为成熟、应用最广泛的出锁方式。安装在基座上的抖动轮强制增加环形谐振腔转动速率，使陀螺出锁。活动部件的加入，一方面引入振动源，使多只激光陀螺通过共同的安装基座互相影响，马仰华等指出，各陀螺的机械抖动互相耦合，引起圆锥误差；另一方面，环形谐振腔通过抖动轮悬臂式安装，使陀螺敏感轴的指向与基座的动力学环境发生关联，产生等效陀螺漂移。由激光陀螺构成的捷联惯组直接与载体固连，工作时受到载体振动、冲击、过载等复杂力学环境的影响，动态误差是影响其精度、限制其应用领域的重要因素。陈熙源等提出了在武器主动段的高动态环境中，传统误差模型难以有效补偿系统误差；Y. M. Zlatkin等提出了Cyclone-4火箭的激光陀螺捷联惯组可能存在与力学环境相关的误差，但并未详细说明产生机理；王巍等指出不断提升激光陀螺的精度，可推动激光陀螺的应用领域由导航级向战略级延伸。Chen Gangli等指出，对激光陀螺捷联惯组进行动力学建模是进行动态误差分析与补偿的基础，提出了一种多体力学传递矩阵分析方法，但并未针对激光陀螺的结构特点对仪表自身动力学特性的影响进行深入分析，也没有对动态误差的量级进行估计。姜睿等指出激光陀螺仪输出与重力加速度的相关性，给出了特定应用条件下偏差的标定方法，表明力学环境对陀螺输出确有影响，但未对大过载、高动态条件下的动态误差进行进一步分析。钟明飞等针对线振动条件下激光陀螺的动态漂移设计了一种滤波估计算法，对振动条件下系统中激光陀螺的动态误差进行估计，但没有对动态误差产生的机理进行说明，也没有介绍抑制动态误差的方法。本文对各激光陀螺间的抖动耦合过程及激光陀螺对外部动态环境的动力学响应进行了分析和计算，估计了误差规模，并进行了仿真验证。针对误差产生的机理，有针对性地总结了误差抑制措施及其效果。

1 机抖激光陀螺及惯性敏感器组件动力学模型

机抖式激光陀螺环形谐振腔通过抖动轮悬挂安装于基座上，抖动轮基本结构及陀螺腔体安装方式如图1所示。环形谐振腔通过胶粘固定在金属衬套上，金属衬套通过安装螺钉与抖动轮连接，抖动轮通过另外4只螺钉安装在基座上。

图1 激光陀螺抖动轮及腔体安装示意图Fig.1 RLG dithering-wheel and installation of resonating cavity

抖动轮可视为绕抖动轴的扭转弹簧，其动力学等效模型如图2所示。机械抖动物理过程可视为由简谐力矩激励的受迫振动，运动方程为

(1)

式中，()=sin()为腔体旋转角；、分别为抖动轮转动阻尼系数和角刚度系数；()为抖动轮的驱动力矩，稳态幅值表达式为

(2)

图2 机抖式激光陀螺动力学模型Fig.2 Dynamics model of MDRLG

为便于进行定量计算，将用到的典型参数列在表1中。

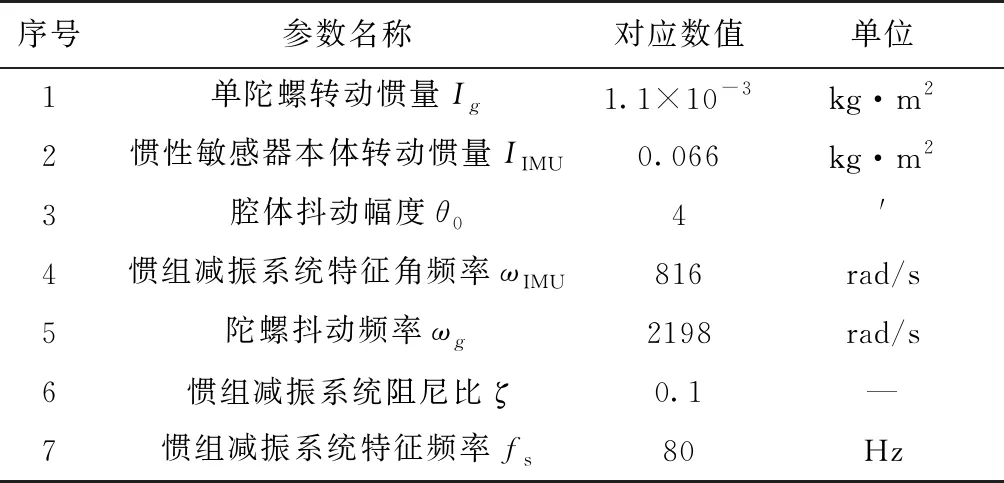
表1 典型参数列表

由表1计算，≈59N·m。由牛顿第三定律，陀螺对安装基座的作用力矩同样为5.9N·m。惯性敏感器组件(以下简称本体)通过橡胶减振器安装于外箱体上，其三维模型及动力学等效模型如图3所示。对本体进行动力学分析，稳态幅值表达式如(3)所示。

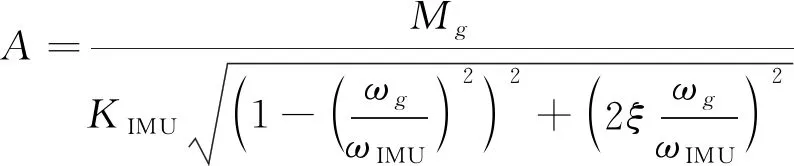
(3)

(4)

式(3)中，表示振动的幅值；为本体减振系统角刚度；为减振系统特征角频率；为减振系统阻尼比。式(4)中，为本体转动惯量。将式(2)、式(4)代入式(3)，得

(5)

将表1各参数代入式(5)，计算出约为4.6″。

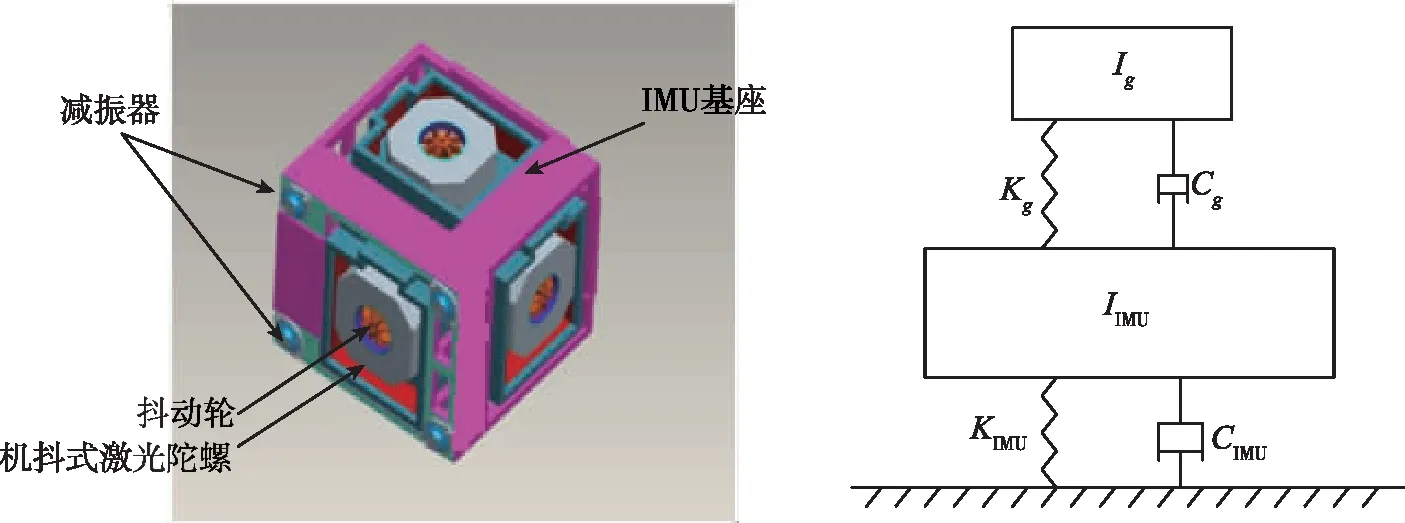
图3 本体三维模型及其动力学模型Fig.3 3D model and dynamics model of inertial sensor assembly

2 静基座机抖激光陀螺间动力学耦合分析

各仪表正交配置的条件下，三陀螺激励将使本体绕本体坐标系各轴做微幅转动，转动角频率为各陀螺抖动频率。以对载体飞行影响较大的陀螺(俯仰)敏感轴为例进行分析，组件及坐标系定义情况如图4所示。

图4 惯性敏感器组件示意图Fig.4 Inertial sensor assembly

系-与本体结构件固连，、、轴与、、陀螺名义敏感轴指向一致；系-与各陀螺敏感轴固连，、、分别与、、陀螺名义敏感轴指向一致；(陀螺)系-与陀螺环形谐振腔固连，轴与陀螺名义敏感轴指向一致，与陀螺名义敏感轴指向一致，与陀螺名义敏感轴指向一致；定系-与捷联惯组箱体固连，、、轴指向与本体坐标系、、指向一致，初始状态，-、-、-、-指向一致。

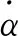
(6)

=sin

(7)

=sin(+)

(8)

式(7)、式(8)中，、为抖动激励的本体运动幅值；、为运动角频率；为两陀螺抖动响应相位差，将式(7)、式(8)代入式(6),得

+)-sin(--)]

(9)

3 外部过载及振动条件下激光陀螺敏感轴变形影响分析

激光陀螺环形谐振腔通过胶与金属衬套粘接，衬套安装柱通过螺钉与抖轮连接，抖轮通过螺钉悬臂安装在基座上。在外部过载及振动条件下，环形谐振腔质量上的合外力使抖动轴将沿力学输入方向产生弯曲形变，陀螺敏感轴指向也随之发生变化，如图5所示。

图5 抖动轴形变示意图Fig.5 Flexure effect of dither axis

3.1 单一过载条件下误差分析

=[,,]

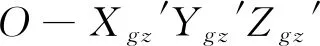
=[sin··sin(),0,cos··sin()]

≐[··sin(),0,·sin()]

(10)

(11)

由-坐标系到-坐标系的状态转移矩阵及陀螺相对本体坐标系的转动速度向量可表示为

(12)

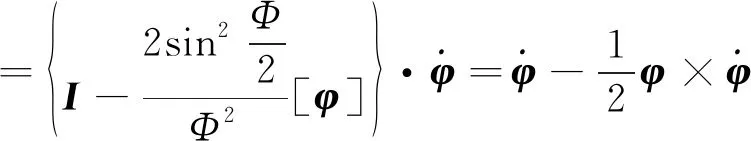
(13)

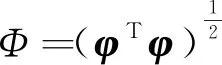
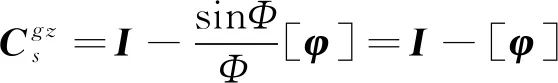
(14)

(15)

陀螺对惯性系输出在陀螺坐标系的测量值可表示为

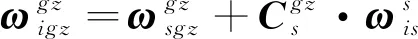
(16)

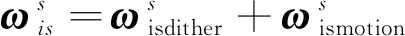
(17)

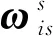
+)-sin(--))]′

(18)

(19)

通过力学仿真，抖动轴形变量与输入加速度近似为线性关系,=,对某RLG-90陀螺，近似为2(″)。以飞行过程力学环境条件为参考，令其轴向加速度最大为15，则约为1.5×10rad。将式(10)、式(11)代入式(15)，得出

[···sin(),0,··sin()]′

将式(10)代入式(14)可得

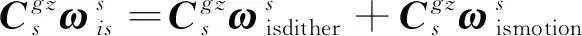
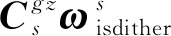
(20)

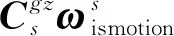
3.2 振动条件下误差分析

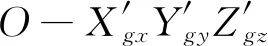
(21)

图6 角速度测量坐标系形变示意图Fig.6 Coordinator flexure of angular velocity

飞行过程中，在外部线振动激励下，本体由于质心与减振系统弹性中心不重合产生线角运动耦合，可引发本体圆锥运动，等效向量如式(17)所示。为外部激励频率，令圆锥运动角振幅为6′。仪表输出为

[0,()sin,()sin]′

(22)

式(22)中前部分为圆锥运动测量值，[0,()sin,()sin]′为由陀螺敏感轴变形引入的误差。考虑飞行中较为典型的随机振动谱，在减振系统的带宽20～200Hz内，0.06/Hz，其振动均方根3.3grams，等效振动输入幅值为4.6g，本体上的振动响应系数为，见表1。根据振动理论

(23)

()(())=

·sin(+)

(24)

式(24)中，根式部分为根据机械振动理论得到的抖轮系统动态放大倍数，表示抖轮弯曲特征频率，某RLG-90陀螺近似为700Hz;表示外部振动在本体上的响应;表示()()的初始相位。

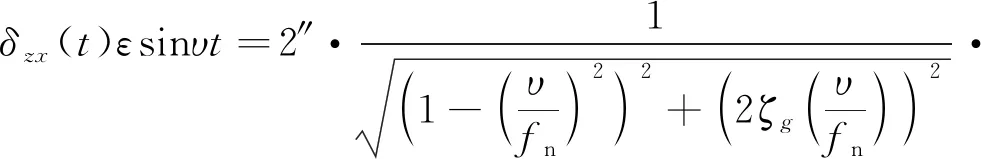
令由0到1000Hz，由0到90°，进行仿真计算，仿真曲线如如图7所示。二维坐标分别为外部振动频率及两方向振动初始相位差。由图7可见,最大误差大于0.03(°)/h。

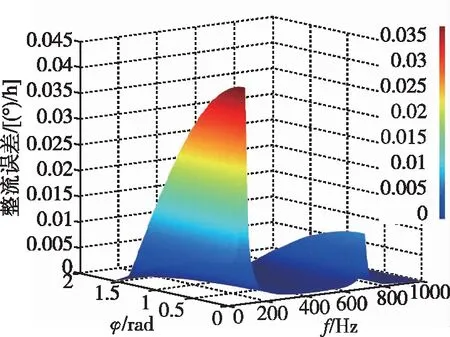
图7 误差仿真曲线Fig.7 Error simulation

分析与小结：图7中，颜色表示误差量级，由蓝色到红色越来越高。由仿真结果可见，在减振器的特征频率及抖轮弯曲特征频率附近，误差明显增大。同时，初始相差越小误差越大。不难理解，在减振器的角特征频率附近，外部振动量级被明显放大，陀螺敏感轴形变也随之变大；在抖轮弯曲特征频率点附近，敏感轴形变量同样明显增大，动态误差也随之呈现相应的变大趋势。

4 抑制措施

根据上文分析，各陀螺抖动耦合产生的误差及激光陀螺敏感轴弯曲形变都会引起激光陀螺捷联惯组角动态误差，针对误差产生的原因，可采取针对性的措施进行抑制。

1)针对抖动耦合误差，需合理选择各陀螺的抖动频率，各抖动频率应相差30Hz以上，减小由各陀螺抖动激励的本体运动产生的圆锥误差。此外，合理地确定陀螺与惯性敏感器组件的特征频率比及转动惯量比，调整本体在陀螺抖动激励下的运动幅度，可减小圆锥效应的幅度，同时在一定程度上抑制抖动耦合误差。

2)应提高激光陀螺抖轮的弯曲刚度，如文献[17]描述的将抖轮的八辐条结构更改为四辐条结构。通过结构仿真，四辐条结构抖轮弯曲刚度可提升50%以上，若减小1/2，根据式(22)，误差可减小1/2左右。为对比八辐条结构更改为四辐条结构后抖轮刚度提升带来的性能改善，对单陀螺进行振动试验(见图8)。试验输入频率范围为20～1000Hz，试验过程中采集陀螺输出。利用高频采样数据分析两陀螺输出中的谱分量，如图9和图10所示，八辐条结构陀螺抖动频率300～400Hz，二阶特征频率600～700Hz，四辐条陀螺抖动频率600～700Hz，二阶特振频率大于1000Hz，说明四辐条陀螺敏感轴刚度明显提升。

图8 单陀螺测试现场Fig.8 Gyro test site

图9 八辐条结构陀螺频谱分析Fig.9 Spectrum analysis of eight-spoked gyro

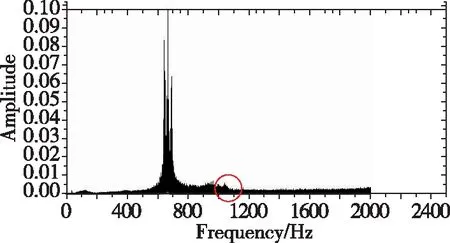
图10 四辐条结构陀螺频谱分析Fig.10 Spectrum analysis of four-spoked gyro

对比2只陀螺百秒输出均值试验前和试验中的变化，详见图11和图12，可见八辐条结构陀螺振动过程中输出变化较为明显，四辐条陀螺振动过程中输出相对平稳。

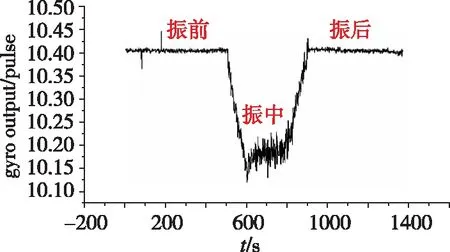
图11 八辐条结构陀螺振动输出Fig.11 Eight-spoked gyro output under vibration testing

图12 四辐条结构陀螺振动输出Fig.12 Four-spoked gyro output under vibration testing

3)还可将激光陀螺抖轮悬臂安装方式更改为由陀螺上下盖板共同固定的三明治式安装方式，如图13所示，可有效保证陀螺敏感轴的稳定性。通过结构仿真，可减小1/2以上，效果非常明显，也是目前主要研究的方向。

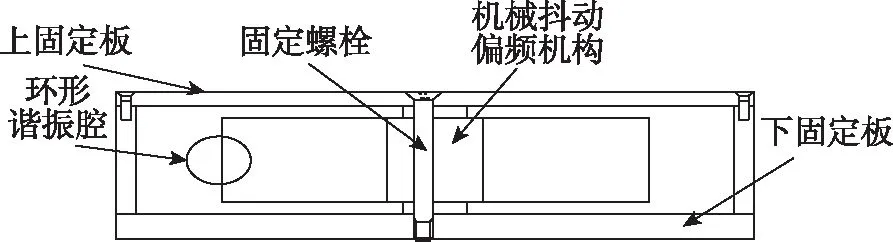
图13 三明治式激光陀螺抖轮系统安装方式Fig.13 Installation of sandwich-type laser gyroscope dithering-wheel

4)文献[18-19]提到的三轴一体激光陀螺组件，如图14所示，只包含一个抖动频率，能有效改善抖动耦合问题。同时在振动条件下，各陀螺敏感轴相对位置关系固定，能有效克服各陀螺敏感轴形变带来的整流误差。

图14 三轴一体激光陀螺Fig.14 Diagram of space triaxial ring laser gyroscope

5 结论

二频机抖激光陀螺间抖动耦合及陀螺敏感轴在动力学环境下的弯曲变形是其动态误差的重要诱因，通过对误差产生机理的建模分析及理论计算，阐明了误差的形成条件及影响规模。1)阶梯配置捷联惯组各激光陀螺的抖动频率，合理选择结构及电路参数能有效抑制抖动耦合误差；2)提升陀螺抖轮弯曲刚度可抑制陀螺敏感轴在高动态条件下变形，以及角动态误差的产生；3)空间三轴陀螺只包含一个抖动频率，能有效抑制抖动耦合误差，3只陀螺在单一微晶玻璃基体上加工完成，确保了3只陀螺在复杂力热环境下的正交精度，也有效抑制了敏感轴变形引入的误差。针对陀螺敏感轴弯曲变形，设计可工程应用的补偿方法是后续进一步提升激光陀螺捷联惯组动态精度的一个重要方向。