基于冲突分类与消解的多智能体路径规划算法设计

王 东，于连波，曹品钊，连 捷

(1.大连理工大学工业装备智能控制与优化教育部重点实验室，大连 116024；2.大连理工大学控制科学与工程学院，大连 116024)

0 引言

多智能体路径规划问题是在已知的环境地图中，为一组智能体规划从各自的起始点到相应目标点的无冲突路径，并实现路径代价总和最小或者最大完工时间最小等优化目标。多智能体路径规划已经广泛应用于各个领域，包括自主仓库管理、多智能体运动规划和无人机集群避障等。多智能体路径规划问题的求解困难程度远大于多个单智能体路径规划问题的叠加，两者的本质区别是多智能体路径规划问题是在规划单个智能体路径的同时消解智能体间的路径冲突。消解冲突是多智能体路径规划问题的关键。

目前主流的一类多智能体路径规划方法为：先分别规划单个智能体的最优路径，然后再消解多智能体之间的路径冲突。冲突消解方案主要有优先级规划法、基于行为的避碰方法、分层地图法以及交通规则法等。这些冲突消解方案简单易行，能够有效消解多智能体间的路径冲突。但上述方案多会牺牲路径长度或智能体运行时间，难以保证多智能体路径规划方案的最优性。

基于冲突搜索(Conflict-Based Search，CBS)的算法是一种经典的多智能体路径规划方法，因其具有最优性和完备性两大优点近年来受到广泛研究。CBS是一种两层搜索算法，算法高层用于找到多个智能体之间的冲突，算法低层将多智能体路径规划问题视为多个单智能体在满足约束下的路径规划。CBS在大地图和智能体耦合度不高的情况下具有较高的求解效率。文献[13]提高了CBS算法的速度，但求得的解只能保证次优性。E.Boyarski等提出了改进的基于冲突搜索算法(Improved Conflict-Based Se-arch，ICBS)，将路径冲突分为关键冲突、半关键冲突和非关键冲突，并对冲突的消解顺序进行优化。ICBS算法保留了标准CBS算法的最优性和完备性，该算法中使用多值决策图对冲突类型进行判断，计算量较大。A.Felner等在关键冲突的基础上，设计了带有启发值的代价函数，减少算法中节点的扩展数量，从而降低算法的计算量。J.Li等规定了一种新的冲突类型，即在网格地图内的某些冲突将必然发生在一个矩形，并提出了相应的检测和消解方法。上述算法多是在CBS的高层进行改进，文献[17]在标准CBS的低层使用了增量式路径规划算法，从智能体的路径重规划方面减少了算法的计算量。

本文设计了一种基于冲突分类与消解的多智能体路径规划算法，以解决多智能体路径规划及路径冲突问题。本文在ICBS算法的基础上，做出以下改进：首先，将多智能体路径中出现的关键冲突类别进一步分类出方向冲突，方向冲突包括相向冲突和交叉冲突；然后，提出方向冲突中相向冲突和交叉冲突的消解方式；最后，提出ICBS高层节点中的冲突搜索算法。本文算法保留了CBS算法的最优性和完备性，并通过新提出的冲突分类及消解方式，减少了ICBS算法高层中约束树的规模，从而减少算法在高层中搜索的时间，一定程度上降低了算法的计算量。

1 问题描述和算法简介

1.1 多智能体路径规划问题模型

多智能体路径规划问题包括一个给定的无向无权图=(,)和多个智能体={,,…,}。无向无权图=(,)中，是图中顶点的集合，是图中顶点间连接边的集合。任意一个智能体∈，拥有唯一的起始顶点∈和目标顶点∈。在多智能体路径规划问题中，时间被离散化为时刻序列={0,1,2…}，在任意一个时刻智能体在当前顶点等待或者移动到相邻顶点，移动和等待两种动作都需要单位代价。智能体的路径被描述为一个从时间序列到顶点集合映射的序列={(0),(1),…,(),…,()}，其中()表示智能体在时刻占用的顶点，表示路径的长度，路径重规划后,的值会随着路径的变化而变化。本文假设智能体保持匀速运行，使用表示智能体的路径代价。智能体路径间不能发生冲突是多智能体路径规划问题的重要约束条件。冲突约束具体描述为：1)任意两个智能体和不能在同一时刻占用同一个顶点，即()≠(),∀,∈∧≠；2)任意两个智能体和不能在时刻和+1时刻间交换彼此占用的顶点，即()≠(+1)∨(+1)≠(),∀,∈∧≠。多智能体路径规划任务是为智能体={,,…,}规划一组从起始顶点到目标顶点的无冲突路径={,,…,}，同时实现路径代价总和最小的优化目标，其中优化目标形式化可表示为

(1)

1.2 CBS算法

CBS算法是解决多智能体路径规划问题的重要算法之一。CBS算法拥有两层结构，其中低层用于规划多个单智能体的最优路径，高层用于解决多个智能体之间存在的路径冲突。CBS算法引入了约束和冲突的概念，约束用一个元组(,,)表示，表示禁止智能体在时刻占用元素，可以是一个顶点或者是一个边，如果表示一个顶点，则该约束表示不允许在时刻占用该顶点，进一步可以表示为(,,)；如果是一条边(,)，则表示禁止在时刻到+1时刻采取的动作占用该边，进一步可以表示为(,,,)。冲突用一个元组(,,,)表示，表示智能体和在时刻同时占用元素；相应地，冲突可以分为顶点冲突和边冲突，分别表示为(,,,)和(,,,,)。

在CBS算法的高层构建一个二叉结构的约束树，约束树中的每个节点包括约束、解和代价三部分。约束树中根节点的约束为空集，每个节点从父节点中继承约束。高层搜索每次从优先级队列OPEN中选取代价值最低的节点进行扩展，若当前节点的解是一组无冲突路径，则将当前节点作为目标节点，并将该节点的解作为问题的解；否则，针对当前节点中的路径冲突，分别添加约束扩展出左右子节点，并添加到OPEN中，重复扩展和添加OPEN中的节点，直到得到具有无冲突解的目标节点。CBS算法低层规划单个智能体满足约束的最优路径，即为高层节点提供解。低层的单智能体路径规划使用任何路径规划算法理论上都可满足CBS的需求，本文使用A算法。CBS算法对于优化路径而言代价是最优的，证明可见文献[12]。

1.3 ICBS算法

CBS算法高层随机选择冲突进行节点扩展，但不恰当的选择会增加约束树的规模，从而增加算法的运行时间。ICBS通过两项改进改善了约束树节点规模较大的问题。不同于CBS算法的随机选择冲突进行节点扩展，ICBS算法将冲突进行优先级划分，分为关键冲突、半关键冲突和非关键冲突。CBS算法对关键冲突拆分出的两个子节点的代价值均大于当前节点的代价值，对半关键冲突拆分出的两个子节点中有且仅有一个子节点的代价值大于当前节点的代价值，对非关键冲突拆分出的两个子节点的代价值均不大于当前节点的代价值。通过优先解决关键冲突和半关键冲突，最后是非关键冲突，在一定程度上加快了算法求解速度。在遇到关键冲突时，ICBS和CBS一样以拆分出该节点的左右子节点的方式来解决，在消解半关键冲突或非关键冲突时不直接将该节点进行拆分，而是试图通过寻找有效的绕路使冲突得到解决。因此，在ICBS算法中，高层节点中除了CBS算法中包含的约束、解和代价三部分以外，还包括该节点中存在冲突个数。

CBS算法及其改进算法侧重消解多智能体间的路径冲突，通过智能体间中心互联式的通信拓扑结构由算法高层直接进行冲突检测。该类算法注重规划满足约束的无冲突路径的最优性，即路径长度最短。文献[18-19]中的适航性、使用Bezier曲线处理单个智能体路径的平滑性等，本文算法暂不进行研究。

2 冲突分类与消解算法

CBS算法和ICBS算法能够为多智能体路径规划问题求解出最优解，但算法单独地处理当前冲突，没有考虑当前冲突的处理与后续路径或其他路径冲突的关系。本章基于当前冲突处理对后续冲突的影响以及优先处理关键冲突对其他路径冲突的影响，对路径冲突进行更加详细的分类并提出相应冲突消解方案。

2.1 冲突分类

在四连通二维栅格地图中，现有的CBS算法消解关键顶点冲突的最佳方案是某一个智能体在冲突发生时刻前进行等待。该方案在消解当前冲突的同时，对于某些特殊类型的关键顶点冲突可能会引起一个新的可预见的冲突，而该新发生的冲突是完全可以避免的。关键冲突具有优先消解权限，智能体在冲突发生前的任意一个时刻等待，均能够消解关键顶点冲突。选择合适的等待时刻，能够在消解当前关键顶点冲突的同时消解其他的半关键冲突或非关键冲突。根据上述分析，本文在ICBS算法的基础上，根据发生冲突的两个智能体的运行方向，将关键顶点冲突进一步分为相向顶点冲突和交叉顶点冲突。本文将冲突定义为={,}，其中=(,,,)表示传统CBS算法中定义的冲突，={,}用于描述冲突类型，表示优先级冲突类型，表示方向冲突类型。

2.1.1 相向顶点冲突

顶点冲突(,,,)中，若智能体和的运行方向完全相反，即智能体和通过冲突顶点后交换占用的顶点，则在本文中该类冲突被定义为相向顶点冲突。通过等待的方式消解该类冲突后，必然会引发一个新的边冲突。下面以图1所示的案例及图2中对应的约束树直观展示相向顶点冲突。

图1中，智能体从起始顶点出发去往目标顶点，智能体从起始顶点出发去往目标顶点。使用CBS算法及ICBS算法为智能体和智能体规划路径，分别为智能体初始规划最优路径={,,,}，为智能体初始规划最优路径={,,,}。智能体和智能体在1时刻共同占用顶点，发生冲突=(,,,1)；在0时刻智能体占用顶点，智能体占用顶点；在2时刻智能体占用顶点，智能体占用顶点，即智能体和智能体在冲突发生的前后时刻交换彼此占用的顶点。

图1 相向顶点冲突案例Fig.1 A case of the opposite vertex conflict

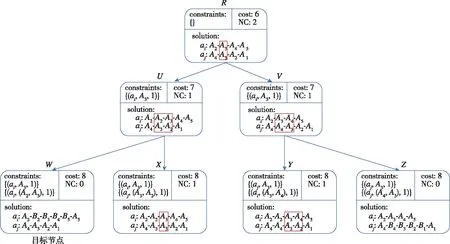
图2 相向顶点冲突案例的约束树Fig.2 A constraint tree of the opposite vertex conflict case

从图2所示约束树的角度来看，依据初始化路径构建约束树的根节点后,检测到根节点中存在顶点冲突=(,,,1)，如图2根节点中红色边框标注所示。为消解顶点冲突，添加约束(,,1)和(,,1)拆分根节点，扩展出左右子节点和。虽然子节点和不存在顶点冲突=(,,,1)，但两个子节点中都产生了新的边冲突=(,,,1)或′=(,,,,1)。为消解该冲突必须再一次进行添加约束和扩展节点的操作，如图2中由节点和扩展出节点、、和所示。

本文将图1和图2展示的在冲突时刻前后交换彼此占用的顶点，并且无法通过一次节点扩展而消解的特殊顶点冲突称为相向顶点冲突=(,,,,,)，表示智能体和在时刻共同占用顶点，在-1时刻和+1时刻交换占用顶点和，下面给出相向顶点冲突的定义。如果一个冲突满足以下条件，那么称其为相向顶点冲突：

1)冲突=(,,,,,)中智能体和将在时刻同时占用顶点，即冲突为顶点冲突；

2)冲突=(,,,,,)是关键冲突；

3)冲突=(,,,,,)中智能体和将交换彼此在-1时刻和+1时刻占用顶点和，即智能体将在+1时刻占用智能体在-1时刻占用的顶点，并且智能体将在+1时刻占用智能体在-1时刻占用的顶点。

2.1.2 交叉顶点冲突

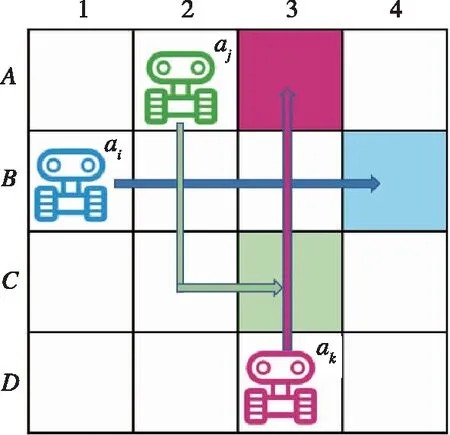
图3 交叉顶点冲突案例Fig.3 A case of the intersect vertex conflict

下面给出交叉顶点冲突的定义，如果一个冲突满足以下条件，那么称其为交叉顶点冲突：

2.2 冲突消解

2.2.1 相向顶点冲突消解方案

消解相向顶点冲突=(,,,,,)时，若采用CBS算法或者其改进算法,则首先针对其中的顶点冲突(,,,)添加一个顶点约束(,,)(或(,,))进行一次节点扩展，然后对随之产生的边冲突(,,,,)(或(,,,,))添加约束(,(,),)(或(,(,),))进行第二次的节点扩展。简言之，CBS算法及其改进算法至少需要进行两次连续的节点扩展才能将相向顶点冲突完全消解，如图2所示。本文消解相向顶点冲突的主要思想是提前为冲突整体添加一个约束，仅进行一次节点扩展便可完全消解相向顶点冲突。具体步骤描述为：

1)检测冲突并判断其为相向顶点冲突=(,,,,,)。

2)针对相向顶点冲突=(,,,,,)，直接分别添加4个组合约束(,,,)、(,,,)、(,;,,,)和(,;,,,)拆分相向顶点冲突所在的节点，扩展出4个子节点。其中，组合约束(,,,)表示智能体在时刻不得占用顶点和；组合约束(,,,)表示智能体在时刻不得占用顶点和；组合约束(,;,,,)表示智能体在时刻不得占用顶点，并且智能体在时刻不得占用顶点和；组合约束(,;,,,)表示智能体在时刻不得占用顶点，并且智能体在时刻不得占用顶点和。

3)新生成的子节点分别调用低层路径规划算法，得到消解相向顶点冲突后的路径。

下面以图1中的案例具体展示相向顶点冲突的消解方案。约束树根节点的构建与ICBS算法相同。检测冲突，进一步判断出其为相向顶点冲突=(,,,,,1)，如图4中节点的红色边框标注部分。对冲突现有的顶点冲突和下一步必然会发生的边冲突直接整体添加两顶点约束(,,,1)和(,,,1)以拆分根节点，扩展出左右子节点，分别如图4中的′和′所示。图4明确展现出经过上述一次节点扩展，即可将相向顶点冲突完全消解。

图4 相向顶点冲突案例的本文方案约束树Fig.4 A constraint tree of the designed scheme for the opppsite vertex conflict case

对比图2和图4可知，本文设计的冲突消解方案与ICBS算法所求目标节点的路径代价值相同，并且本文设计方案的约束树节点扩展数量小于ICBS算法。表1在算法的高层扩展节点数、高层生产节点数以及低层算法调用次数方面具体展示本文设计方案的优势。

表1 相向顶点冲突案例算法指标对比

对于相向顶点冲突=(,,,,,)，CBS算法及其改进算法至少需要两次连续的节点扩展才能完全消解冲突。本文设计方案仅需一次节点扩展便能完全消解冲突。本文设计方案在路径代价方面与ICBS算法具有相同的最优性，并且对计算量要求较低，能够减小算法搜索空间规模和算法搜索时间。

2.2.2 交叉顶点冲突消解方案

图5 交叉顶点冲突案例的约束树Fig.5 A constraint tree for the intersect vertex conflict case

本文设计了针对交叉顶点冲突的消解方案，选择合适的智能体，让其在恰当等待时刻进行等待，保证在消解当前交叉顶点冲突的同时消解其他半关键冲突或者非关键冲突，进而减小算法搜索空间以及算法搜索时间。

交叉顶点冲突的消解方案描述如下：

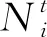
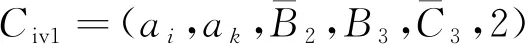
图6 交叉顶点冲突案例的本文方案约束树Fig.6 A constraint tree of the designed scheme for the intersect vertex conflict case

对比图5和图6可知,本文设计的交叉顶点冲突消解方案与ICBS算法所求目标节点的路径代价值相同，并且本文设计方案的约束树节点扩展数量小于ICBS算法。表2在算法的高层扩展节点数、高层生成节点数以及低层算法调用次数方面具体展示本文设计方案的优势。

表2 交叉顶点冲突案例算法指标对比

2.3 基于冲突分类与消解的多智能体路径规划算法

综合本文提出的相向顶点冲突和交叉顶点冲突分类与消解方案，根据CBS算法及其改进算法，现给出基于冲突分类与消解的多智能体路径规划算法，如算法1所示。输入一个多智能体路径规划实例后，首先用低层A算法分别为每个智能体规划最优路径并计算路径代价，进而构建出根节点，将根节点插入到OPEN列表，如算法第1～2行所示。第3～14行是算法检测冲突和添加约束消解冲突的主体部分。第5行调用搜索高层节点中的冲突算法检测冲突，并根据本文给出的相向顶点冲突和交叉顶点冲突分类判断冲突类型，具体见算法2。第9～13行根据本文所提的方向冲突添加不同的约束进行冲突消解，其中第9、10行是相向顶点冲突的检测与约束添加，第11、12行是交叉顶点冲突的检测与约束添加，第13行生成新的子节点，具体见算法3。算法1最终为输入的多智能体路径规划实例输出一组无冲突最优路径。

算法2展示了高层节点冲突检测与类型判断方案，检测本文所提的方向冲突并将冲突返回给算法1。算法2中增加了半关键和非关键冲突列表以及智能体冲突表。半关键和非关键冲突列表分别保存各智能体发生的半关键和非关键冲突，智能体冲突表保存各智能体的等待时刻，为消解交叉顶点冲突提供相应信息。

算法1:基于改进冲突搜索的冲突分类与消解算法输入:一个多智能体路径规划实例输出:该实例的一个最优解1调用低层A*算法为每个智能体规划初始最优路径2生成根节点R,并将其放入OPEN列表3while OPEN列表非空时 then4 从OPEN中取出代价值最低的节点,作为当前节点N5 调用搜索高层节点中的冲突算法检测冲突6 if节点N中没有冲突且不是关键冲突then7 调用低层A*算法重规划绕行路径8 else节点N中存在冲突且是关键冲突then9 if相向顶点冲突then10 添加组合约束11 else交叉顶点冲突then12 添加约束并确定智能体等待时刻13 生成子节点N'并将其放入OPEN列表14节点N中没有冲突15返回路径规划的解

算法2:搜索高层节点中的冲突算法输入:一个约束树中的节点N的解输出:节点N中存在的冲突C1for智能体中的任意一个组合对(ai,aj)then2 if智能体ai和aj间存在冲突C then3 if冲突C是关键冲突then4 判断相向顶点冲突或交叉顶点冲突5 返回 C6 else if冲突C是半关键冲突then7 将C放入半关键冲突列表8 else then9 将C放入非关键冲突列表10 更新智能体冲突表11 返回第一个半关键或非关键冲突

算法3展示了用约束集合生成新的子节点的算法，和ICBS算法不同之处在于添加的约束是本文设计的针对冲突类型消解方案的组合约束。

算法3:生成新的子节点输入:一个约束树中的节点N和对智能体添加的约束输出:生成的新的子节点1将对智能体添加的约束加入到节点N原有的约束2调用低层路径规划算法更新智能体路径3生成新的子节点N'

3 实验与仿真

本章进行对比实验，以验证本文设计算法求解多智能体路径规划问题的优越性。首先，本文设计的基于冲突分类与消解的多智能体路径规划算法(ICBS-DC)与采用优先级方法消解路径冲突、使用蚁群算法规划智能体路径的多智能体路径规划方法(Ant-PP)相比，展现出求解结果质量的优越性，即求解结果路径代价方面的优越性。然后，将本文算法与CBS算法以及ICBS算法进行对比，体现本文算法在计算量方面的优势。本章所有实验的代码均采用Python编写，均在参数为2.3GHz Intel Core i5-6300HQ 8GB RAM的笔记本电脑上进行。使用大小为8×8的四连通二位栅格地图，其中障碍物占比为地图大小的20%，在每次实验中障碍物均随机生成。对比实验中智能体数量从1到15逐个增加，并且在每个智能体数量下随机生成100个多智能体路径规划案例，取各项实验数据的平均值作为最终数据。

图7和图8分别展示了本文ICBS-DC算法和使用优先级的Ant-PP算法的成功率与路径规划方案的路径代价。其中，成功率采用文献[12]中描述的在5min时间限制内,算法能够求解出结果的案例数量与案例总数量的比值。由图7和图8可知，本文的ICBS-DC算法的成功率与路径规划方案的路径代价均优于Ant-PP算法，并且随着智能体数量的增加，ICBS-DC算法的优势越加明显。

为了验证本文算法在计算量方面的优势，将本文ICBS-DC算法与CBS及ICBS进行对比实验，分别比较三种算法的成功率、运行时间、高层约束树节点扩展数量以及低层路径规划算法平均调用的次数，结果如图9～图12所示。

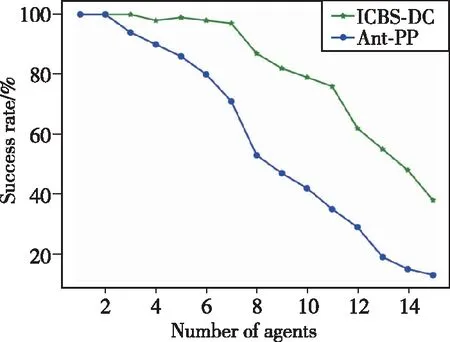
图7 ICBS-DC和Ant-PP成功率对比Fig.7 Success rates of ICBS-DC and Ant-PP algorithms

图8 ICBS-DC和Ant-PP路径代价对比Fig.8 Path costs of ICBS-DC and Ant-PP algorithms

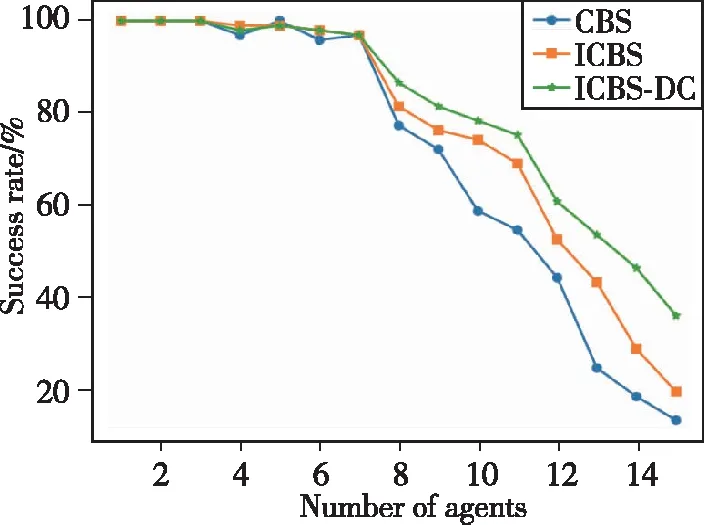
图9 三种算法成功率对比Fig.9 Success rates of three algorithms

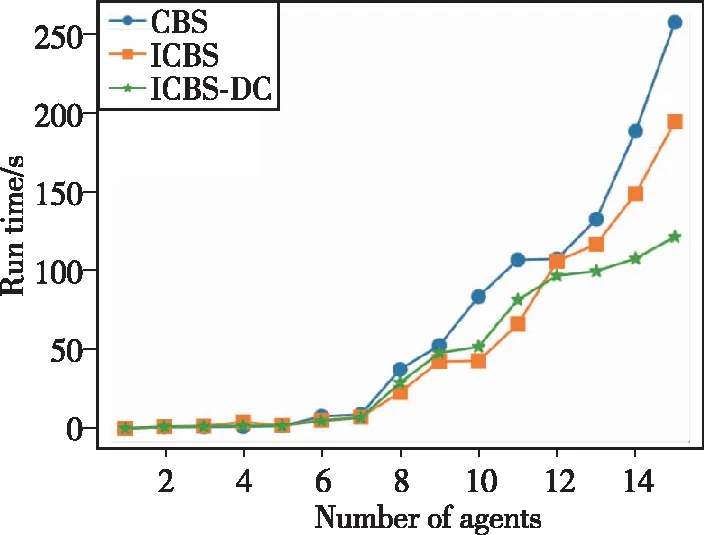
图10 三种算法运行时间对比Fig.10 Run times of three algorithms

图11 三种算法节点扩展数量对比Fig.11 Number of extension nodes of three algorithms

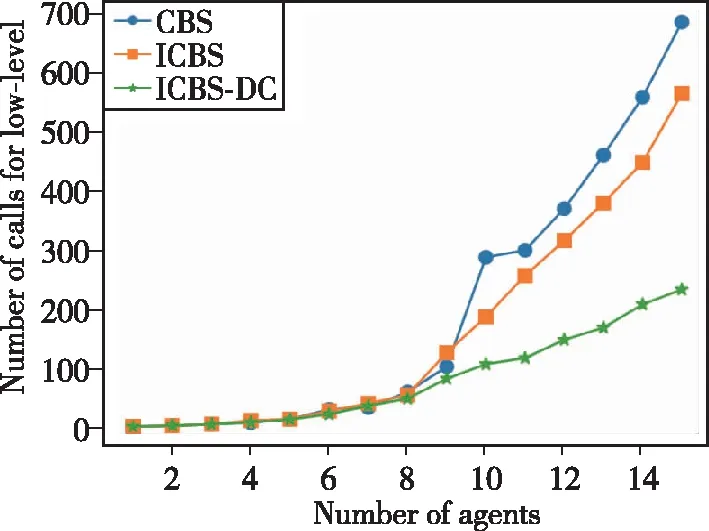
图12 三种算法调用低层路径规划次数对比Fig.12 Number of calls for low-level of three algorithms

当智能体数量较少时，各个智能体的路径之间发生冲突的可能性较小，由图9～图12所示结果可以看出，三种算法在成功率、平均运行时间、高层约束树节点扩展数量和低层路径规划算法调用的次数等方面几乎具有相当的性能。当智能体数量较多时，各智能体的路径在环境中发生更多的冲突，由图9报告的结果可知，CBS算法在智能体数量较多时，其解决多智能体路径规划问题的成功率下降速度最快，其次是ICBS。ICBS-DC相比CBS和ICBS而言，在智能体密度较大的情况下具有更高的成功率。而就图10报告的平均运行时间而言，ICBS-DC运行速度虽然比CBS快，但相较于ICBS在某些情况下速度稍慢，然而随着智能体数量的不断增加，智能体的路径之间冲突的可能性增加，ICBS-DC算法的平均运行时间的增长速度与CBS和ICBS相比较为平缓，说明ICBS-DC在智能体比较密集的环境下展现出更好的运行时间优势。

由图11和图12展现的高层和低层的指标来看，ICBS-DC在高层约束树节点扩展数量及低层路径规划次数方面均少于CBS和ICBS，但这正是ICBS-DC在一些情况下耗时增加和平均运行时间增长速度稍慢的原因。ICBS-DC为了能使高层约束树节点扩展的数量减少，在算法2中对产生的关键冲突再判断其是否属于本文提出的方向冲突，并在算法1中对冲突进行捕捉。当环境中产生的关键冲突较多时，判断方向冲突又在一定程度上增加了运行时间。图11和图12报告的结果符合ICBS-DC的主要目的：一方面减少了高层约束树节点扩展数量，使得约束树的规模减小；另一方面使得低层路径规划调用次数减少。因为算法高层每生成一个节点就会给相应智能体添加约束，调用低层路径规划算法对该智能体进行重新规划，所以图11和图12具有相似的曲线走势。当高层约束树中节点数量不是很多时，ICBS算法的运行速度与ICBS-DC相当，甚至在一些情况下要快于ICBS-DC；但当智能体数量较多时，使用本文所提的冲突消解方案可以有效对约束树的规模进行限制，从而减小高层算法的搜索时间，这与图10中报告的ICBS-DC的平均运行时间在智能体数量大于12时增长速度相比ICBS较为缓慢是一致的，说明ICBS-DC在智能体密集的环境下能展现出更好的求解速度优势。

4 结论

本文设计了一种基于冲突分类与消解的多智能体路径规划算法，以解决多智能体路径规划中的路径冲突问题。本文将多智能体路径冲突中的关键冲突进一步分类出相向顶点冲突和交叉顶点冲突，并针对这两类冲突类型提出相应的消解方案：1)相向顶点冲突的消解方案以添加两点约束的方式，避免了在消解该类冲突的过程中引发的新冲突，减少算法高层约束树节点扩展数量，减小约束树规模，降低算法运行时间；2)交叉顶点冲突的消解方案通过选择恰当的智能体等待时刻，在消解该类冲突的同时消解其他冲突，提高算法的搜索效率。最后通过仿真实验验证了本文提出的冲突分类与消解方案能够为多智能体路径规划问题求解出路径代价最优的解，并且能够有效减少算法高层约束树节点的数量以及低层路径规划算法的调用次数，进而加快算法的求解速度。

未来的研究工作包括以下两点：1)本文算法是基于四连通二维栅格地图设计的，未来考虑将本文算法扩展到三维空间的其他类型地图；2)在二维及三维环境中进行实物实验，验证本文算法的有效性。