基于块状有理Krylov方法的大地电磁三维模型降阶正演

周建美 刘文韬 鲁凯亮 李 貅

(长安大学地质工程与测绘学院，陕西西安 710054)

0 引言

大地电磁(MT)方法广泛应用于地壳研究[1-2]、岩石圈地幔调查[3-6]、资源勘探[7-11]和海洋调查[12]等领域。MT方法是一种典型的频域电磁测深方法[13]，工作频率范围可达10-5～104Hz[14]。MT三维正演方法可以分为以下几类：积分方程法[15-17]，有限差分方法[18-23]，有限体积方法[24-25]，有限元方法[26-32]以及无网格法[33]等。无论采用哪种正演方法，都需要求解多个频率的大型稀疏线性方程组[34]。MT响应频率范围通常很大，可能达到5个或更高数量级，每个数量级范围内通常包含5～10个采样频点[35]。此外，在每个频率上都需要针对x方向TE极化源和y方向TM极化源进行两次正演[27]。因此，一次MT正演一般需要求解几十个大型稀疏线性方程组，计算量很大。

学者们对此提出了多频电磁正演加速方法。Um等[36]引入了一种针对迭代法的预处理重复利用技术，只需求解最低频率的ILU预处理矩阵，并将该预处理矩阵重复应用于其他频率的正演计算，从而减少正演计算时间。但该算法对于较大频率间隔情况下(比如MT)的正演模拟的有效性还有待验证。另一种常用方法是并行计算技术[37]，即采用多CPU计算设备并行计算多个频率的正演响应[38-39]。上述两种改进算法本质上都是基于不同发射频率正演响应的独立求解，当发射频点数增加时，方程求解次数或CPU数量也需要相应增加。

相对上述两种方法，Krylov子空间算法[40-43]更有效。随频率变化的电场响应可以表示为一个传递函数与源矢量的乘积[40]，Krylov子空间算法可对其有效求解。Druskin等[40]基于多项式Krylov子空间近似的谱Lanczos方法(SLDM)求解上述电场响应表达式，但该算法的收敛速度依赖于频率范围和模型的电导率差异[41]。相对而言，有理Krylov子空间方法[41-44]的收敛性更好，且收敛性不依赖于模型电导率差异和空间网格分布。但是该算法需要求解多个极点的大型线性方程组。采用重复极点，结合直接求解器，可以显著提高求解速度。

尽管Krylov子空间算法可以求解人工源频率域多频电磁响应，但是该方法不能直接推广到MT正演求解。MT正演假设源是无限大的平面波源，通常采用边界条件隐式代替源的作用[18-19]，相应的MT正演响应不能表示为一个传递函数与矢量的乘积形式。Kordy等[45]基于二次场方法，将MT响应表示为一个传递函数与二次场矢量的乘积形式，从而可以采用Krylov子空间算法进行求解，但是由于二次场是随频率变化的，因此求解每一个频率的正演响应时都需要重新构建一次Krylov子空间。为此，Kordy等[45]引入一种有理插值技术解决这一问题，但仍需要多次正演计算生成有理插值方法所需的训练集，因而相比常规的逐次求解各个频率正演响应的方法，该方法仅仅获得2～4倍的加速。

不同于Kordy等的处理方法，本文将MT的源显式表示为一个位于高空的平面电流的形式[46]，该源对于所有频率都是一个常数。当平面电流位于模型上边界时，与Zhang等[47]直接在模型上边界赋值电场为1等效。在此基础上，可以将MT响应表示为一个传递函数与常数源矢量的乘积形式，从而可以采用有理Krylov方法求解MT响应[47]。

与可控源电磁法正演问题不同[42]，模拟MT响应需对每一个频率计算TE和TM极化源的两次正演，这等价于一个多源正演问题。块状Krylov技术广泛应用于多源正演问题，可有效提高计算效率[48-50]。为进一步提高MT正演的计算速度，不同于Zhang等[47]直接采用有理Krylov方法进行求解，本文引入块状有理Krylov技术[51]，将TE和TM极化源表示为块状源矢量，将求解两个极化源的正演响应简化为构建一个块状有理Krylov子空间。

极点是有理Krylov方法的一个重要参数，极点的选取会影响方法的计算速度和计算精度。Güttel[52]对极点的选取算法进行了总结，提出了一种最优化极点选取方法，即通过全局搜索得到多个最优化重复极点[50]。基于该方法，本文引入一种更简单、有效的方法获取最优化单个重复极点[42]，结合直接法求解器[53]，可实现MT三维模型的高效正演模拟。

本文首先介绍基于拟态有限体积的空间离散化方法[54]，源项显式表示为面电流分布，从而将MT响应表示为传递函数与常数源矢量乘积的形式； 然后，使用块状有理Krylov(BRK)算法获得传递函数的模型降阶近似解； 最后，通过典型的一维半空间模型和3D都柏林测试模型1(DMT1)正演[34]，验证本文算法的计算精度和计算速度。

1 正演算法

1.1 控制方程离散

设电磁场随时间的变化关系为eiωt，忽略位移电流，则MT正演对应的控制方程为[14]

∇×E+iωB=0

(1)

∇×μ-1B-σE=S

(2)

式中：E和B分别表示电场强度矢量和磁场强度矢量； 角频率ω=2πf，其中f是频率；μ是磁导率；σ是电导率；S是外加源项，显式表示为平面电流分布[46]。采用自然边界条件，利用基于交错网格的拟态有限体积方法[54]，得到空间离散后的控制方程

Ce+iωb=0

(3)

CTMμb-Mσe=s

(4)

式中：C是离散形式的旋度算子；Mμ和Mσ分别是包含模型磁导率和电导率信息的离散矩阵，具体形式参见文献[42]；e、b和s分别为离散形式的电场、磁场和发射源项。对于三维MT正演，同时考虑TE和TM极化源，采用如图1所示的平面电流近似，平面电流位于空气层中一定高度，可得空间离散的源项为

图1 TE极化模式(左图中蓝色箭头)和TM极化模式(右图中橙色箭头)的平面电流源分布示意图

[H(x-xi)-H(x-xi+1)]

i=1,2,...,nx-1;j=1,2,...,ny

(5)

[H(y-yj)-H(y-yj+1)]

i=1,2,...,nx;j=1,2,...,ny-1

(6)

s=[s1,s2]

(7)

消去式(4)中的磁场，得到关于电场的控制方程

(A+iωI)e=-iωX

(8)

e(ω)=gω(A)X

(9)

1.2 块状有理Krylov方法

采用Krylov子空间方法近似求解gω(A)X，由于X是一个块状矩阵，因此可采用BRK方法一次性求解所有源的正演响应[51]。给定块状矩阵X和单个重复极点ξ，BRK方法采用Gram-Schmidt正交化方法求解得到有理Krylov子空间的基，由一系列的块状矢量v1,v2,…,vm+1构成，这里m表示子空间的维度。针对单个矢量和块状矩阵的有理Krylov方法(算法1)的程序实现见表1[50]。

表1 算法1——块状有理Krylov方法

(10)

为了实现算法1，还需要预先给出极点ξ和迭代次数m。本文采用单个重复极点ξ，其值可通过近似收敛率公式快速得到[42]。对于频率范围T=[ωmin,ωmax]，最优化极点为

(11)

得到最优化极点ξ后，可以采用替代算法[42]快速得到最优化迭代次数mopt。根据周建美等[42]的分析，频率为ωmin和ωmax时，收敛率最差(模型降阶解满足给定残差阈值所需迭代次数最大)，但是最低频率ωmin对应的相对误差最大，因此可以简单地选择最低频率ωmin对应的模型降阶解的相对误差不再降低时的m作为mopt。由于已知最优化的单个重复极点ξ，本文求解mopt的替代算法较Börner等[41]提出的方法更加简化，算法的具体计算机实现过程算法2如表2所示，其中：L0=diag(λ1,λ2…,λN)为替代对角矩阵，λ1,λ2，…,λN是[λmin=10-8,λmax=108]范围内N=500个对数等间隔分布的值；mmax为一个足够大的数，本文取mmax=200；R(m)表示Rm的集合; arg minR(m)表示寻找R(m)中最小Rm所对应的m。

表2 算法2——求解mopt的替代算法

图2 fmax/fmin固定时不同fmin条件下有理Krylov解的相对误差error随m的变化曲线

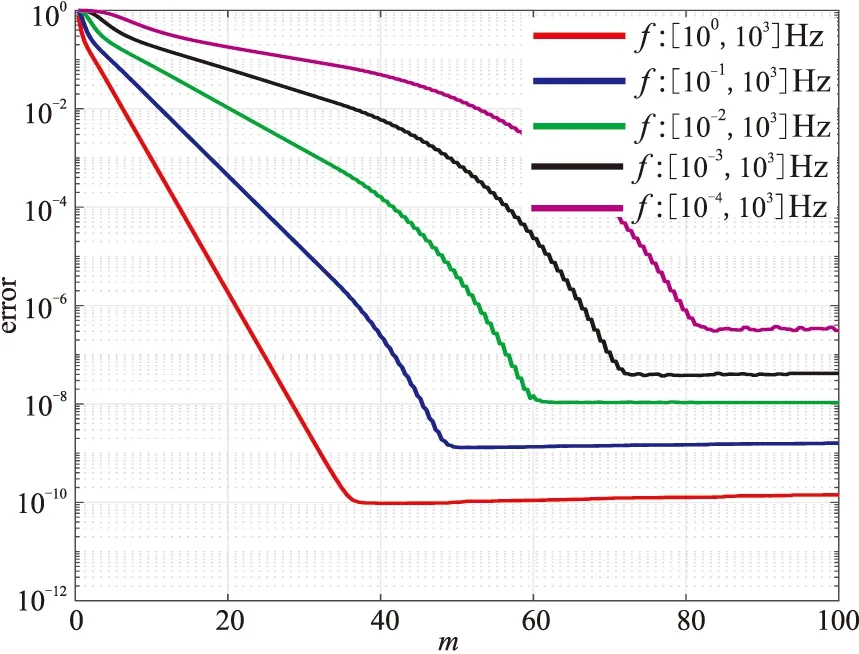
图3 求解频率范围的fmax固定时不同fmin的有理Krylov解的相对误差error随m的变化曲线

1.3 MT响应

张量MT勘探典型的测量参数是地表水平电场Ex、Ey及全磁场分量Hx、Hy、Hz。假定有两个正交极化源，阻抗张量为

(12)

其中下标“1”和“2”分别代表TE和TM极化模式。基于阻抗张量Z定义视电阻率和相位[13]分别为

(13)

(14)

式中：下标“q”和“p”代表x或y； Re(·)和Im(·)分别表示取实部和虚部。

2 数值实例

通过两个典型模型的正演验证BRK方法对MT正演计算的速度和精度。数值实例中空气层电阻率均为1×106Ω·m。本文计算设备为32G内存、四核主频3.6GHz的Intel i7CPU的台式电脑。

2.1 均匀半空间模型

采用BRK方法计算MT响应。根据式(11)得到最优化极点ξ=-0.1987。采用替代算法求解mopt。图4为频率fmin为0.001Hz时的有理Krylov子空间解的相对误差error随m的变化曲线。由图可见，m>70时，error小于1×10-6且基本恒定，满足计算精度要求，因此选取mopt=70。

图4 均匀半空间模型fmin=0.001Hz的有理Krylov解的error曲线

图5为不同h时计算的视电阻率和相位正演结果与解析解的对比。对于均匀半空间模型，TE和TM模式的响应是相同的，因此图5仅给出了TE模式的正演结果。

由图5可见，在低频时，靠近地表(h=0.5δ)时，平面电流源不能较好地近似为平面波源，因此正演响应存在较大误差； 当平面电流源逐渐远离地表(h=4δ，8δ，12δ)时，正演误差逐渐减小； 当平面电流源位于空气层边界(h=16δ)时，所有频点视电阻率相对误差均小于1%，相位误差均小于0.5°。

图5 半空间模型不同h的MT视电阻率(a)和相位(b)响应与解析解对比

均匀半空间模型计算结果表明，将平面电流源置于空气层边界时，本文BRK方法能够精确地模拟MT三维正演响应。

为了分析BRK方法的计算效率，对比本文BRK方法、非块状有理Krylov方法[42](RK)和逐次采用直接求解器PARDISO[53]求解各个频率的正演响应的直接求解法(Direct)的计算结果。虽然一维模型的TE模式和TM模式的响应是相同的，但是为了通用性考虑，在比较算法计算效率时，本文依然以计算TE和TM模式响应的总计算时间为依据。上述三种算法计算的MT响应基本相同，因此本文仅对计算时间进行比较，结果如表3所示。可见，本文BRK方法只需1次系数矩阵分解及70次矩阵回代； RK方法分别求解TE和TM模式的响应，因此需要1次系数矩阵分解和140次矩阵回代； 直接求解法(Direct)需对每个频率进行1次系数矩阵分解，因此共计需要31次系数矩阵分解和31次矩阵回代。因此，本文BRK方法相比直接求解法，能够显著提高计算速度，加速比高达22.5； 相比RK方法，由于减小了1次子空间构建的运算次数，也能实现一定的加速效果。

表3 均匀半空间模型MT响应模拟不同算法计算量及耗时对比

2.2 三维DTM1模型

为了进一步分析BRK方法的精度和速度，利用三维都柏林测试模型1(DTM1)[30]进行正演响应计算，并与有限元法和积分方程方法的正演结果进行对比。

DTM1模型的均匀半空间包含3个块状电性异常体，具体参数见表4和图6。坐标原点位于块体1中心点的正上方地表，观测点位于坐标原点，fmin=10-4Hz，fmax=10Hz，在计算频率范围内对数等间隔取21个频点。计算区域离散为72×74×72个网格，最小网格长度为20m，网格放大系数为1.5。

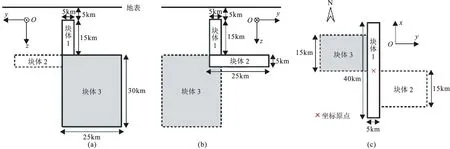
图6 DTM1模型示意图

表4 DTM1模型块体空间坐标和电阻率

根据式(11)得到最优化极点ξ=-0.1987，与一维模型的最优化极点值相同，因为极点取决于最低频率和最高频率的乘积。采用替代算法求解mopt。图7为fmin=1×10-4Hz的有理Krylov子空间解的相对误差error随m的变化曲线。相比一维模型，三维DTM1模型的求解频率范围更大，因此最小频率fmin对应的误差收敛率更小，从而相对误差稳定时所对应的m更大。由图7可知，m>150时，相对误差基本恒定，因此选取mopt=150。

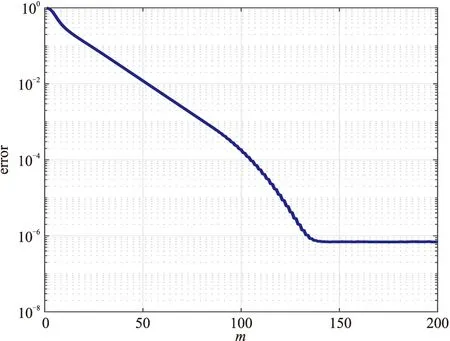
图7 fmin=1×10-4Hz时有理Krylov子空间解的error随m的变化曲线

采用本文BRK方法得到的DTM1模型正演结果见图8。文献[32]给出了多种方法的DTM1模型正演响应，其中积分方程法(IE)[55]和有限元法(FE)[27]的结果基本重合，因此本文以这两种算法的正演结果作为参考，验证本文算法的精度。由图8可知，BRK方法正演得到的xy和yx分量的视电阻率(ρxy，ρyx)和相位曲线(φxy，φyx)，与积分方程法[55]和有限元法[27]的结果基本重合； BRK方法正演得到的xx和yy分量的视电阻率(ρxx，ρyy)和相位(φxx，φyy)，在高频段(>1Hz)由于视电阻率值太小没有显示，相位分布也相对杂乱； 但是在低频段(<1Hz)，本文计算结果与积分方程法和有限元法的结果基本一致。因此，本文BRK方法能够较精确地正演MT三维复杂模型的电磁响应。

统计本文BRK法、RK[42]法和Direct法[53]开展DTM1模型正演的耗时如表5所示。相比Direct法，BRK法加速比达到11.8； 相比RK方法，也能实现一定的加速效果。相比一维半空间模型，三维DTM1模型的正演加速比有所降低，主要原因在于三维DTM1模型求解的频率数量仅为21，每个数量级范围内仅选取4个频率，相比一维半空间模型(频率数量为31)有所减少，因而直接求解法所需的计算时间相对减少，导致BRK方法的加速效果相对下降。

3 讨论

MT正反演中如何选取频点一直是一个开放的问题[56]，一般采用对数等间隔选取方法，每个数量级范围内选取3～4个频率[57]或者更少[58]，少数情况下选取5～6个频率[59]甚至8个频率[60]。由于采用直接求解方法，每个频率都需要求解2次大型线性方程组，因此应选取尽量少的频率[56]。

采用本文BRK子空间方法则可以很好地避免上述问题。对于BRK子空间方法，增加求解频率数量，只是增加了求解模型降阶解方程(式(10))的次数。由于式(10)是小维度矩阵的传递函数求解，计算速度很快，因此相应增加的计算时间可以忽略。如果按照一维均匀半空间模型的频率分布密度采样，即在1×10-4～1×10Hz频率范围内计算51个对数等间隔分布的频率，对这些频点计算MT响应，BRK方法耗时仅为2988.5s，相比21个频率的MT响应计算时间2894.2s，增加了30个计算频率，但求解时间仅增加94.3s，即增加1个频率所需计算时间仅为3.1s。而采用直接求解法计算51个频率的正演响应，所需时间高达83504.2s，相比计算21个频率的计算时间34391.1s，意味着增加30个频率所需求解时间增加49113.1s，即增加1个频率的正演响应所需要的时间高达1637.1s，为BRK方法所需时间的528倍。计算51个频率的正演响应，BRK方法相比直接求解法的加速比高达27.9。显然，求解频点数越多，BRK方法的计算速度优势越明显。

图9为采用BRK方法计算的51个频率和21个频率的MT响应结果，这里仅给出通常基于xy和yx分量计算的视电阻率和相位。如图9所示，51个频率的MT视电阻率和相位曲线，相比21个频率的MT曲线，更能够体现曲线变化的细节特征。因此，在计算时间允许的条件下，建议选取尽可能多的频点数，可得到更精细的响应曲线特征。

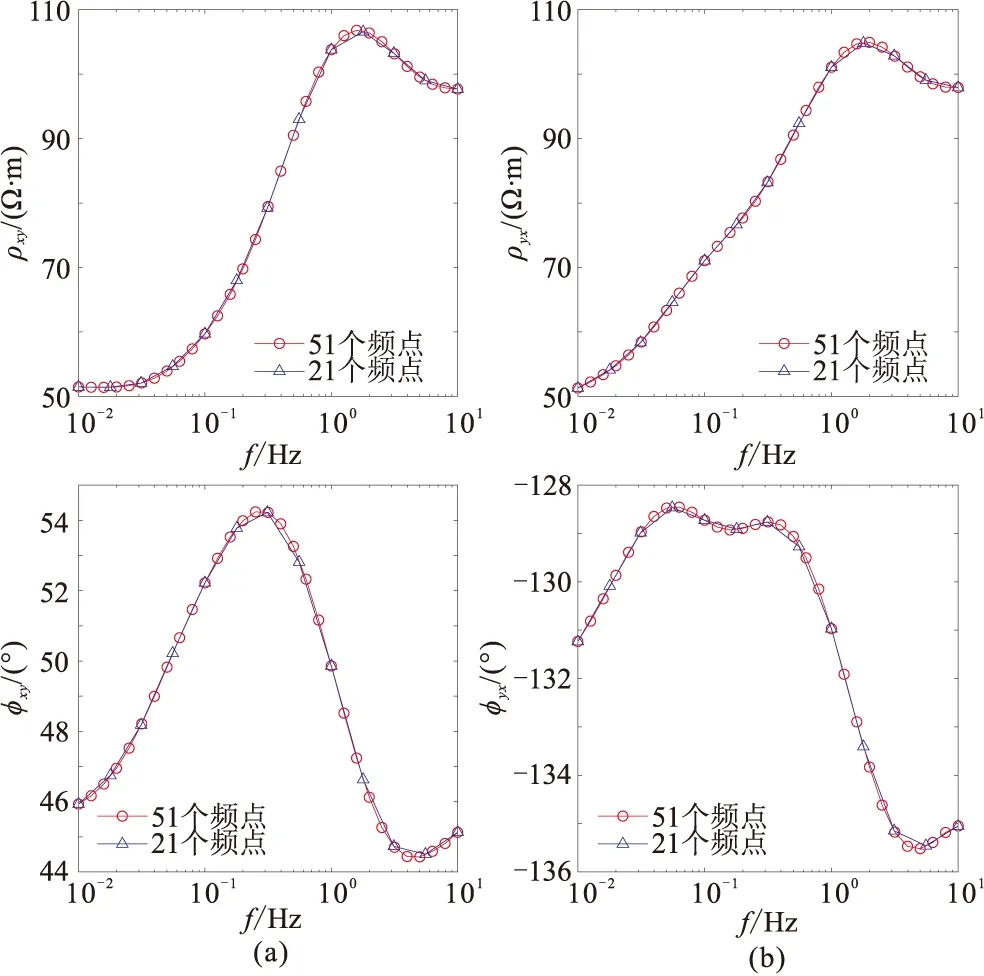
图9 DTM1模型采用BRK方法计算的不同频点的视电阻率(上)和相位(下)

4 结论

本文基于拟态有限体积离散和块状有理Krylov方法实现了一种求解MT三维正演响应的快速算法。通过将源显式表示为高空中的平面电流源，可将任意频率的MT正演响应表示为一个传递函数与源矢量的乘积。采用块状有理Krylov方法，只需要构建一次块状有理Krylov子空间即可实现TE和TM极化源在给定频率范围内所有频点的MT正演响应。采用渐近收敛公式得到块状有理Krylov方法的最优化单个重复极点，利用替代算法可快速得到最优化的Krylov子空间维度，结合直接求解器，将MT三维正演的计算量减小为一次系数矩阵分解和多次矩阵回代。相对常规的直接求解方法，本文方法极大地提高了计算速度。

均匀半空间模型的数值实例结果表明，将平面电流源设置在空间离散网格中空气层的最外边界区域，能够最大限度地近似为平面波源，降低正演近似误差。计算31个频率的半空间模型正演响应，相比直接求解方法，块状有理Krylov方法在保证计算结果精度的同时，实现了22.5倍的加速； 计算21个频率的三维DTM1模型的正演响应，相比直接求解方法，块状有理Krylov方法实现了11.8倍的加速。求解频率数越多，块状有理Krylov方法的计算速度优势越明显。

本文块状有理Krylov方法的主要计算量为1次系数矩阵分解和mopt次回代，因此对于中小尺度模型，当求解频率数量较多时，本文算法在计算速度上优势显著。当模型的空间离散网格数量较大、需要求解的频率数量较少时，直接分解算法的计算时间和占用内存都会显著增加，此时基于迭代算法逐次求解各个频率响应的传统方法在计算速度上更具有优势。因此，实际工作中要根据模型规模和频率数量选择合适的正演求解方法。