套管抗拉可靠性强度研究
2022-10-08徐蔼彦姬丙寅史交齐
徐蔼彦,姬丙寅,史交齐,李 岩
(1.西安三维应力工程技术有限公司,陕西 西安 710061; 2.中国石油天然气股份有限公司 塔里木油田分公司,新疆 库尔勒 841000)
引 言
随着油田勘探开发的迅速发展,深井、高温井、高压井、以及非常规井、富含CO2、H2S和Cl-等腐蚀介质的油气井越来越多,套管在石油钻井及油田开采过程中起着至关重要的作用,选择不当会导致频繁出现各种形式的套管失效事故[1-3],且事故率呈不断上升的趋势,给油田带来巨大的经济损失,也给油田的安全稳定生产带来严峻的挑战,因此,高强度性能已成为套管选型的主要依据之一[4-6]。
目前,国际上广泛认可并使用的套管抗拉强度计算方法是历史上API管体屈服强度计算方法,且最新的ISO10400—2018标准采用的也是相同的计算方法,该公式是在统计大量试验数据的基础上获得,由于受过去试样水平的限制以及实验条件的影响,事实上已经偏于保守。近几年,由于套管的各项参数控制精度和性能水平已经有了很大的提高,实际的连接强度已经高出历史上API计算公式的额定值,可见该公式已不能正确反映不同质量套管的强度差异,这给套管强度设计和应用带来了较多疑难问题[7-9]。至今为止,国内外专家学者在套管抗拉强度方面进行了相关的研究,研究内容仅限于可靠性方法的讨论,还未有制定科学规范或统一标准[10-13]。因此,科学合理的建立一种能够反映套管产品连接强度参数统计特性的套管可靠性强度计算方法是一项亟待解决的艰巨任务,具有重要工程应用价值。
为此,本文以API管体屈服强度计算公式为基础,采用一次二阶矩方法对套管的抗拉可靠性强度进行计算,其中随机变量关键参数由试验获得,同时采用有限元模拟计算和实物试验进行验证和评估。
1 理论计算
套管抗拉可靠性强度理论计算方法及过程是在API管体屈服强度计算公式的基础上,通过管体拉伸屈服强度对应的极限状态方程,考虑模型不确定度,采用一次二阶矩法[14]计算套管的抗拉强度,进而计算套管抗拉可靠性强度,计算过程如下:
(1)对套管进行几何尺寸测量和材料拉伸试验,通过统计分析方法获得连接强度计算的关键参数(平均外径、平均壁厚、材料抗拉强度)。
(2)计算管体连接屈服强度(API公式):
FYAPI=fymnAp。
(1)
(3)对应的极限状态方程:
F=πfy(D-t)t。
(2)
(4)按同厂家同批次同规格套管的实物试验值/计算值获得模型不确定度mu,则管体抗拉强度计算公式:
F=muπfy(D-t)t。
(3)
(5)对式(3)进行一次二阶矩法偏微分计 算:
(4)
根据fy、t和D的分布计算F分布的公式:
(5)

(6)
(6)抗拉可靠性强度计算公式:
Fdes,n=F-k·SF。
(7)
式中:FYAPI为管体屈服强度,kN;fymn为规定最小屈服强度,MPa;Ap为管体横截面积,mm2;F为管体抗拉强度,kN;fy为材料抗拉强度,MPa;D为平均外径,mm;t为平均壁厚,mm;mu为模型不确定度(mu=0.968 10,标准差为0.052 57);SF为标准平方差,kN;Fdes,n为某置信度的抗拉可靠性强度,如n取0.95时Fdes,0.95表示95%置信度的抗拉可靠性强度,对应的目标可靠性水平为0.5%;k为每一失效概率对应的常数。
为了验证上述套管抗拉可靠性强度理论计算公式的正确性,选取油田常用规格套管,进行关键参数获取、抗拉可靠性强度理论计算、有限元模拟计算及实物试验验证与评估。
2 有限元模拟计算与实物试验
2.1 试验材料及方法
试验材料:10根Ф177.80 mm×10.36 mm 110 套管,化学成分为(质量分数):0.25% C、0.27% Si、0.53% Mn、0.001% P、0.003% S、1.16% Cr。
几何尺寸测量:10根试样,每根试样长3 500 mm,每根测量50个截面,相邻两截面间隔70 mm,每个截面8等分测量4组外径值和8组壁厚值,共测2 000组外径值和4 000组壁厚值,测量示意图如图1所示。
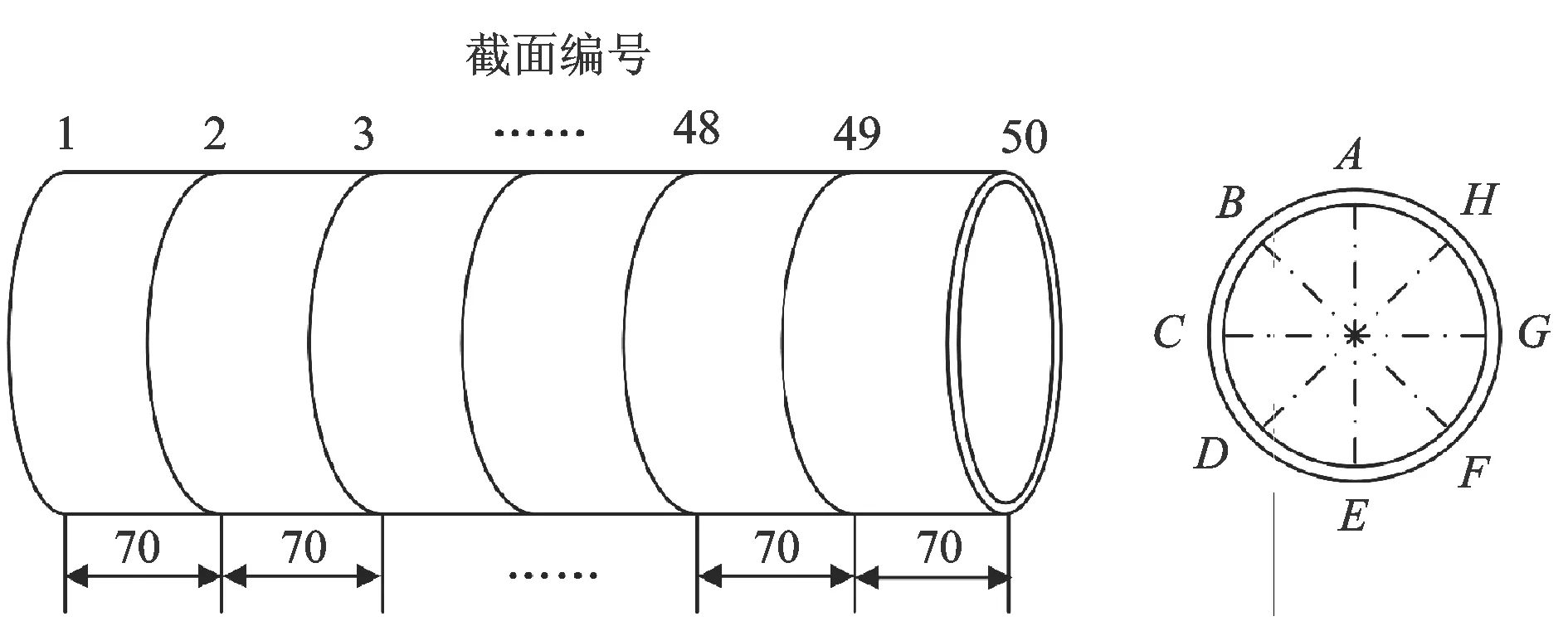
图1 几何尺寸测量示意图Fig.1 Schematic diagram of geometric dimension measurement
材料拉伸试验:10根试样,对每根试样分别进行15组25.4 mm×65.0 mm板状材料拉伸试验,采用SHT4106型电液伺服万能试验机,按照ASTM A370-18标准要求,进行材料拉伸试验,共得到148组数据。
实物试验:10根试样,上述几何尺寸测量完成后,在管体上截取3 500 mm管状试样, 采用外压挤毁试验机, 按照API RP 5C5—2017标准要求,进行全尺寸实物拉伸试验,共得到10组实物拉伸数据。
2.2 有限元计算模型
以本文试验获得的关键参数(平均外径、平均壁厚、材料抗拉强度、模型不确定度)建立三维有限元计算模型,模型采用理想弹塑性材料模型,PIPE16单元网格,弹性模量取205 GPa,泊松比取0.3,套管长度取3 500 mm,建立的模型如图2所示。

图2 有限元计算模型图Fig.2 Finite element model
3 计算与试验结果及分析
3.1 关键参数获取
几何尺寸测量、材料拉伸试验结果统计分析见表1及图3所示。可见, 试验测得的平均外径为179.26 mm,标准差为0.039 0;平均壁厚为10.68 mm,标准差为0.037 4;标准差均较小,试验结果统计数据均较好地服从正态分布。试验测得的材料抗拉强度平均值为989 MPa,标准差为11.490 3,试验结果统计数据也服从正态分布。

表1 各参数测试结果统计表Tab.1 Measurement results of test sample parameters

图3 各参数测试结果统计分布图Fig.3 Statistical distribution of measurement results of various parameters
3.2 理论计算分析
采用本文抗拉可靠性强度理论计算公式(1)—(7)及10根Ф177.80 mm×10.36 mm 110套管试验
所得关键参数平均外径、平均壁厚、材料抗拉强度,对10根套管抗拉可靠性强度进行理论计算,计算结果见表2和图4所示。
由表2可见,抗拉强度理论计算值为5 497 kN,目标置信水平为0.005的TRL0.005的均值为5 195 kN。由图4可见,套管抗拉强度理论计算值的目标置信水平的5 195 kN远高于订货技术协议值的4 130 kN,说明试样抗拉性能良好,能满足油田使用要求。

表2 抗拉可靠性强度的理论计算、有限元模拟计算及试验结果Tab.2 Tensile reliability strength of test samples obtained by theory calculation, finite element simulation and tests

图4 抗拉可靠性强度理论计算分布图Fig.4 Distribution of theory calculation results of tensile reliability strength
3.3 有限元模拟计算验证
10根Ф177.80 mm×10.36 mm 110套管抗拉可靠性强度有限元模拟计算结果见表2。由表2可见,抗拉强度有限元模拟计算值为5 525 kN,大于抗拉可靠性强度理论计算值的目标置信水平的5 195 kN,验证了本文抗拉可靠性强度理论计算方法的可靠性。典型有限元模拟计算结果如图5所示(试样编号:8Y),该试样抗拉强度为5 502 kN。
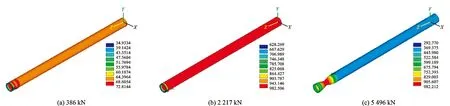
图5 有限元模拟计算结果典型图Fig.5 Typical figures of finite element simulation calculation process
3.4 实物试验验证
10根Ф177.80 mm×10.36 mm 110套管实物拉伸试验结果见表2。由表2可见,实物试验值为5 496 kN,大于抗拉可靠性强度理论计算值的目标置信水平的5 195 kN,验证了本文抗拉可靠性强度理论计算方法的可靠性。
典型实物试验结果如图6所示(试样编号:8Y),该试样抗拉强度为5 569 kN。

图6 实物试验结果典型图Fig.6 Typical figure of physical test result
3.5 综合分析
抗拉可靠性强度的理论计算、有限元模拟计算及试验结果如图7所示。由图7可见,Ф177.80 mm×10.36 mm 110套管抗拉可靠性强度理论计算值的目标置信水平的5 195 kN,小于有限元模拟结果5 525 kN和实物试验结果5 496 kN,且有限元模拟结果与实物试验结果基本吻合,验证了本文抗拉可靠性强度理论计算方法的可靠性。
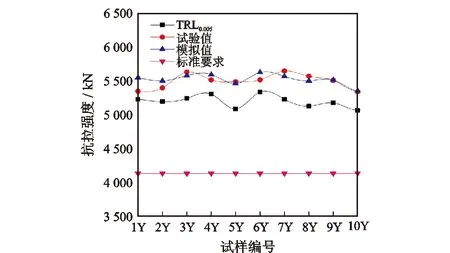
图7 抗拉可靠性强度的理论计算、有限元模拟计算及试验结果Fig.7 Theory calculation, finite element simulation and test results of tensile reliability strength
4 结 论
(1)试验得Ф177.80 mm×10.36 mm 110套管的计算抗拉可靠性强度为5 497 kN,标准差为117.1 kN,目标置信水平TRL0.005的5 195 kN,其值小于理论计算结果(5 497 kN)。
(2)此理论计算结果与有限元模拟结果(5 525 kN)及实物试验结果(5 496 kN)基本吻合,说明利用一次二阶矩法计算套管抗拉可靠性强度的理论计算方法可用来评价不同可靠性水平下同批次套管抗拉强度的可靠性。
