某掘进机主轴轴承系统方案的仿真分析

吕海霆，董淑婧，魏延刚，刘彦奎，张志东

(1. 大连科技学院 机械工程学院，辽宁 大连 116052；2.大连交通大学 机械工程学院，辽宁 大连 116028)

悬臂式掘进机是我国能源开掘行业重大基础技术装备，20世纪60年代开始从仿造一步步向自主设计制造发展，目前，我国整机制造能力已经接近国际先进水平.与整机制造行业的繁荣发展不同，掘进机关键零部件仍然依赖进口，其中主轴承几乎全部依赖进口，并且单个主轴承成本最高可以占掘进机的二十分之一左右.当前，德国的罗特艾德、IMO、FAG和瑞典的SKF占有掘进机主轴承的绝大部分市场份额.掘进机能否有效、可靠运行是巷道设备能否正常运行的关键.作为掘进机关键支撑部件，掘进机主轴承承担了主要的回转支撑任务.主轴承工作状态的稳定和使用寿命的长短对掘进机安全高效生产具有重要影响[1-2].

近些年我国部分工程技术人员开始对掘进机主轴的受载状况和主轴承的优化设计进行研究.应用滚动轴承设计理论和有限元等方法对主轴承选型、静力分析和振动特性分析，并对轴承寿命、结构优化等进行了有益的研究工作[3-9].

某特殊型号掘进装备要求适应大坡度、薄煤层、窄机身和矮机身等条件，存在受载较大但设备尺寸有严格限制的问题，导致其主轴直径与支撑轴承尺寸形成矛盾.在保证主轴强度和刚度的前提下，轴承的尺寸被极大压缩，必须使用非标轴承，但在试验中仍然存在使用寿命相对较低的问题，极大地限制了掘进装备的使用效率.

为了提高掘进装备的可靠性和使用效率，在分析原主轴支撑方案的基础上，从改善该掘进装备主轴支撑方案入手，根据材料力学和轴承设计基本原理，设计出四个相对合理的主轴轴承支撑系统方案.为了最终确定最优方案，应用工程分析软件RomaxDesigner对四个不同的主轴轴承系统进行仿真分析，研究在给定工况下四种支撑方案中不同轴承的载荷分布和接触应力分布，确定轴承滚动体的受载数目、受载最大滚动体的位置、滚动体的最大载荷和滚动体的最大接触应力.对比分析四种轴承支撑方案的优劣，确定出最优的方案，并为最优方案的各轴承的优化设计提供基本条件，对其中受载最重的轴承进行结构尺寸的设计优化，为该型号掘进机主轴轴承系统的设计与制造提供参考.

1 主轴轴承支撑系统方案

1.1 主轴轴承支撑方案

根据该机型使用的实际工况条件，以断面扫掠运动的最大设计载荷来研究轴与轴承的使用性能.断面扫掠运动的设计载荷为：径向载荷Fr=46(t)，轴向受载Fa=18(t).

由于该型悬臂式掘进机的使用条件限制，轴承外径最大不能超过355 mm，同时为了保证轴的强度，轴的最小直径不得低于280 mm.这就极大地限制了轴承的可选择范围，同时在SKF、FAG和NSK等轴承厂商提供的轴承中均没有适合此应用条件和尺寸要求的产品.因此所有设计方案中的轴承均需要重新设计，以便满足给定的设计要求.由于对轴承内部尺寸做了较大幅度的改变，以往对轴承选用的经验与实际轴承的实际性能之间有可能出现较大偏差，带来未知的可靠性问题.为了减少试验方案的数量和缩短试验时间，有必要对各种设计方案及设计的轴承进行仿真对比.

综合主轴和轴承的尺寸限制和实际工况条件，根据材料力学和轴承设计基本原理，设计出相对合理的四种主轴轴承布置方案，为描述方便称这四个方案分别为：方案A、方案B、方案C和方案D.四个方案的轴承在轴上安装位置均相同，只是轴承类型和尺寸有所不同，图1所示为四个方案的装配示意图.

(a) 方案A

方案A选用的轴承类型和相应的布置方式为：4个相同的调心滚子轴承(设代号为：A20000)和1个双列四点接触球轴承(设代号为：ABQJ0000)；主轴左端布置2个调心滚子轴承，右端为2个调心滚子轴承和1个双列四点接触球轴承.

方案B与方案A的差别只是将调心滚子轴承换成了圆锥滚子轴承(设代号为：B30000)：主轴左端布置为同向布置的2个圆锥滚子轴承，右端为方向与左端圆锥滚子轴承反向布置的2个圆锥滚子轴承和1个双列四点接触球轴承；两两反向的圆锥滚子轴承形成了背靠背安装的圆锥滚子轴承对.

方案C选用的轴承类型和相应的布置方式为：2个相同的圆锥滚子轴承(设代号为：CD30000)和1个双列调心滚子轴承(设代号为：CD20000)；主轴左端为一个圆锥滚子轴承(CD30000)，右端为方向与左端圆锥滚子轴承反向布置的一个圆锥滚子轴承和双列调心滚子轴承；两个反向的圆锥滚子轴承形成了背靠背安装的圆锥滚子轴承对.

方案D选用的轴承与方案C的相同，只是圆锥滚子轴承的布置方向与方案C的相反，两个圆锥滚子轴承形成的是面对面安装的圆锥滚子轴承对.

1.2 各轴承尺寸设计

由于结构尺寸要求的限制，轴承的尺寸参数无法采用标准值，而是参照国家标准GB/T 288、GB/T 294和GB/T 297尽量取推荐的值或取接近推荐的值.

表1、表2为调心滚子、圆锥滚子轴承的设计尺寸，其中长度单位为mm，角度单位均为(°)；代号ABQJ0000的双列四点接触球轴承的主要尺寸如下：外径为355 mm ；滚珠直径为23 mm；内径为285 mm；内圈滚道挡肩直径为312.8 mm；宽度为80 mm；外圈滚道挡肩直径为331.2 mm；接触角为35°；内圈滚道半径为11.96 mm；列间距为40 mm；外圈滚道半径为11.96 mm；滚珠数为29；内滚道曲率中心偏移量为0.404 4；滚珠节圆直径为322 mm；外滚道曲率中心偏移量为0.404 4.

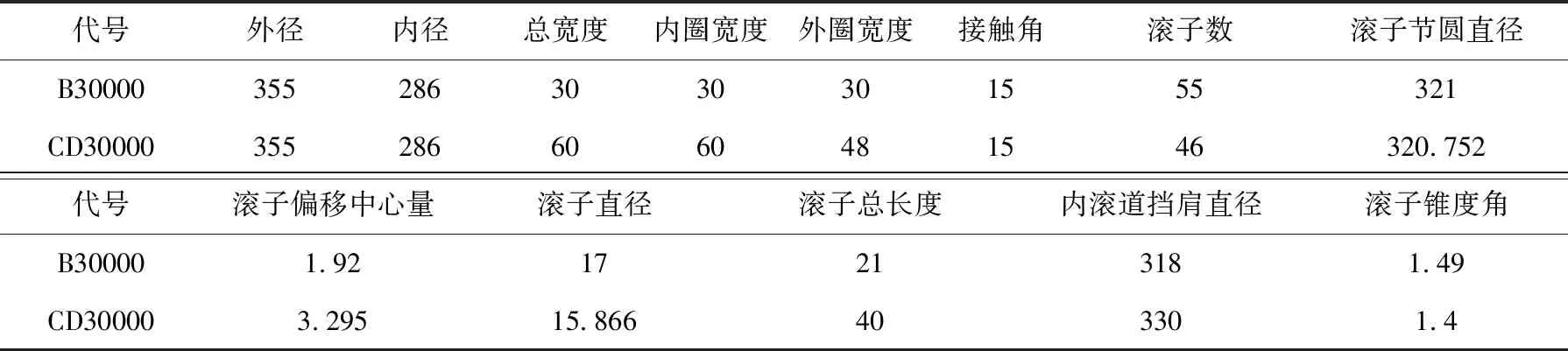
表2 圆锥滚子轴承主要尺寸

2 主轴轴承支撑方案的仿真分析

为了确定四种轴承支撑方案的优劣，必须对四种轴承支撑方案进行全面的力学分析，包括对主轴的变形和应力分析，轴承的载荷分布和应力分析.工程分析软件Romax Designer为全面分析主轴轴承系统提供了有效的技术手段.

2.1 Romax仿真模型的建立

四种布置方案中载荷添加形式均为距右侧轴端150 mm处添加点载荷，根据工况条件施加相应的径向力和轴向力；轴承相对于轴的安装位置也相同.轴承约束方式各方案有所不同，方案A的轴承约束方式是左右各两对调心滚子轴承和双列四点接触球轴承内圈相对于轴的位置固定，外圈接地固定.方案B轴承约束方式是左端两列轴承内圈轴向左侧约束，外圈轴向右侧约束；右端两列轴承安装方式相反为轴承内圈右侧约束，外圈左侧约束；四点接触球轴承采用内圈相对于轴的位置固定，外圈接地固定.方案C轴承约束方式是左端轴承内圈左侧约束，外圈右侧约束；右端轴承内圈右侧约束，外圈左侧约束；双列调心滚子轴承内圈相对于轴的位置固定，外圈接地固定.方案D轴承约束方式是左端轴承内圈右侧约束，外圈左侧约束；右端轴承内圈左侧约束，外圈右侧约束；双列调心滚子轴承固定方式与方案C相同.为节省篇幅，在此仅给出方案D的轴承仿真模型图，见图2.

图2 方案D的仿真模型

2.2 轴的位移和应力对比分析

根据Roamx仿真计算结果可以看出，因为不同方案中轴承相对于轴的位置完全相同，所以轴的径向位移呈现出相同的变化趋势，都是轴的中段与悬臂段出现两个轴的位移峰值，在轴承位置趋近于零.中段位移峰值大于悬臂段的位移峰值.A、B、C和D四个方案轴中段最大径向位移值分别为379、436、453和307 μm.

四种方案中轴的应力变化趋势也基本相同，最大应力位置均在右侧轴承组处.A、B、C和D四个方案轴的最大应力分别为28、36、34和35 MPa.

2.3 轴承整体受力和最大接触应力对比分析

表3列出了四种方案所有轴承的整体受力情况.需要说明的是滚子类轴承存在边缘效应，但是通过滚子母线修形等技术可以避免边缘效应，表中滚子类轴承最大接触应力是滚子对数修形后的应力值.

表3 四种方案各轴承的整体受力和最大接触应力

方案A中受载最大的是双列四点接触球轴承和右调心滚子轴承2.这两个轴承承受了总径向负载的81.89%，其中右调心滚子轴承受到径向力178 200 N占比35.56%，双列四点接触球轴承承受径向力232 200 N占比46.33%；轴向载荷几乎全部由双列四点接触球轴承承受，其所受轴向力为176 200 N，占总轴向负载的99.91%；力矩几乎都由四点接触球轴承承受.右调心滚子轴承的最大滚道接触应力为2 026.81 N，四点接触球轴承最大滚道接触应力为3 541.73 MPa.这种负载分布情况说明，四点接触球轴承与调心滚子轴承组合使用可以较好地分配径向载荷，同时由于本身轴承特性有较好的适应冲击载荷的能力.但在径向和轴向载荷同样较大的工况条件下，因为调心滚子轴承不能单独承受轴向载荷造成四点接触球轴承受到复合负载太大，而球轴承的承载能力相对较差，易导致四点接触球轴承最大接触应力过大出现损坏.

方案B为背靠背布置的两对串联的圆锥滚子轴承代替了方案A中的两对调心滚子轴承，右侧三个轴承所受径向力占总径向载荷依次为19.09%、45.08%和24.85%；所受轴向力占总轴向载荷依次为14.22%、34.35%和40.03%.右侧三个轴承的轴承组承担大部分轴向载荷、径向载荷和力矩，且径向和轴向载荷分布都相对均匀.其中受载相对较大的右圆锥滚子轴承2受到径向力和轴向力为242 000 N和78 480 N，双列四点接触球轴承受到径向力和轴向力为133 400 N和91 480 N.作为主要受载的两个轴承，右圆锥滚子轴承2虽然受到复合载荷相对更大但由于滚子轴承更强的受载能力，它的最大接触应力为2 283.95 MPa，小于双列四点接触球轴承的最大接触应力3 121.13 MPa.方案B中四点接触球轴承的径向力和轴向力比方案A的四点接触球轴承分别少了42.55%和48.08%.在受载大幅减小的情况下，最大接触应力仅减少11.88%.方案B的轴承仿真结果说明四点接触球轴承与圆锥滚子轴承的组合可以较好地满足径向载荷和轴向载荷同时存在的使用场景.但在重载条件下，四点接触球轴承相对于其他滚子类轴承在最大接触应力上具有明显劣势.

方案C将承载能力不强的双列四点接触球轴承更换为承载能力更强同时又有调心作用的双列调心滚子轴承.将串联布置的两对圆锥滚子轴承更换为一对圆锥滚子轴承.方案C中双列调心滚子轴承承受径向力为545 600 N，占轴承总径向载荷的85.19%，所受轴向力为40 930 N，占比为21.49%.右圆锥滚子轴承承受径向力为69 810 N，占轴承总径向载荷的10.90%，所受轴向力为142 500 N，占比为74.80%，力矩也主要由其承受.从仿真结果看到，双列调心滚子轴承承受了大部分径向载荷，右圆锥滚子轴承承受大部分轴向载荷.与方案B相比，方案C中右圆锥滚子轴承最大接触应力为1 763.97 MPa，比方案B的右圆锥滚子轴承2小了22.77%.双列调心滚子轴承的最大接触应力为2 389.21 MPa，比方案B中双列四点接触球轴承小了23.45%.方案C虽然载荷分布相对集中，但调心滚子轴承与圆锥滚子轴承的组合能够较好发挥调心滚子轴承有高径向承载性能的优点，同时圆锥滚子轴承具有较高的轴向承载能力，避免了调心滚子轴承无法承受轴向载荷的缺点.

方案D是将方案C中背对背布置的圆锥滚子轴承变为面对面布置.主要受载轴承为左圆锥滚子轴承和双列调心滚子轴承.与方案C相比，各个轴承所受径向载荷分布变化不大，主要径向受载轴承仍为双列调心滚子轴承，为513 700 N，占总径向负载的89.09%.主要的轴向受载轴承则由方案C的右圆锥滚子轴承变为左圆锥滚子轴承，为136 700 N，占总轴向载荷的69.26%，双列调心滚子轴承受轴向力50 160 N占比为25.42%，与方案C相差不大；值得注意的是，方案D的力矩基本上是由两个圆锥滚子轴承分担.方案D中左圆锥滚子轴承最大接触应力为1 509.12 MPa，与方案C右圆锥滚子轴承相比减少了14.45%.双列调心滚子轴承最大接触应力为2 410.11 MPa，与方案C相比增加了0.87%.从仿真结果可以看出，方案D在双列调心滚子轴承最大接触应力几乎没有增加的情况下，圆锥滚子轴承的最大接触应力有一定程度的减少.根据四个方案轴承的最大接触应力分析结果看，方案C和D都大大地好于方案A和B，且方案C和方案D的最大接触应力相差很小，仅为0.87%.

综合四种轴承布置方案轴的径向位移、应力，所有轴承的受载和应力分析的结果，可以认为方案D为四种方案中的最优方案.

2.4 轴承的载荷分布与应力分布分析

由于相同种类的轴承在受载情况相同的情况下，其载荷分布和应力分布具有相似性，另外，对四种方案中轴承的载荷分布和应力分布结果证明了方案D是最优方案，在此主要给出方案D与其他方案载荷分布和应力分布等的结果比较.

2.4.1 圆锥滚子轴承

方案D和方案C受力最大的圆锥滚子轴承的内外圈滚道载荷分布如图3所示，由图可知，全部的滚子均参与承载，滚动体在270°的位置受载最大，大小分别为12 720 N和15 520 N.对比B、C、D方案中的圆锥滚子轴承受力可知，单一承受径向载荷时，载荷分布在滚道上约180°的范围内；在承受轴向载荷为主的联合载荷时，所有圆锥滚子均承载，且轴向载荷占比越大，滚道载荷分布越均衡.

图3 圆锥滚子轴承内外圈滚道载荷分布

方案D和方案C受力最大圆锥滚子轴承的最大接触应力分布雷达图如图4所示.由图可见，内外滚道都是周向360°的范围内所有与滚子接触处都有接触应力，内滚道的接触应力大于外滚道的接触应力，而且各滚动体与套圈接触区域的最大接触应力相差不大，最大接触应力出现在周向270°的位置，其值分别为1 509 MPa和1 764 MPa；最大接触应力构成的雷达图接近圆形，方案D比方案C更接近圆形.

图4 圆锥滚子轴承内外圈最大滚道接触应力分布

方案D和方案C受力最大的圆锥滚子轴承内滚道接触应力云图如图5所示，且两者均在90°和270°的位置出现了应力值的增加和滚子接触应力等高线的偏移.这是由于这两个轴承均承受来自轴的正弯矩，而方案C和方案D圆锥滚子轴承安装方向相反，所以方案C右圆锥滚子轴承接触应力等高线在90°位置向滚子大端偏移，在270°的位置向滚子小端偏移；相反，方案D左圆锥滚子轴承接触应力等高线在90°位置向滚子小端偏移，在270°的位置向滚子大端偏移.

(a)方案D左

2.4.2 双列调心轴承

由于方案C和方案D中的双列调心滚子轴承结构尺寸完全一样，受力相差不大，滚道载荷分布和应力分布相似，所以仅对方案D中双列调心滚子轴承进行分析.方案C中双列调心滚子轴承的滚道载荷和接触应力不再赘述.

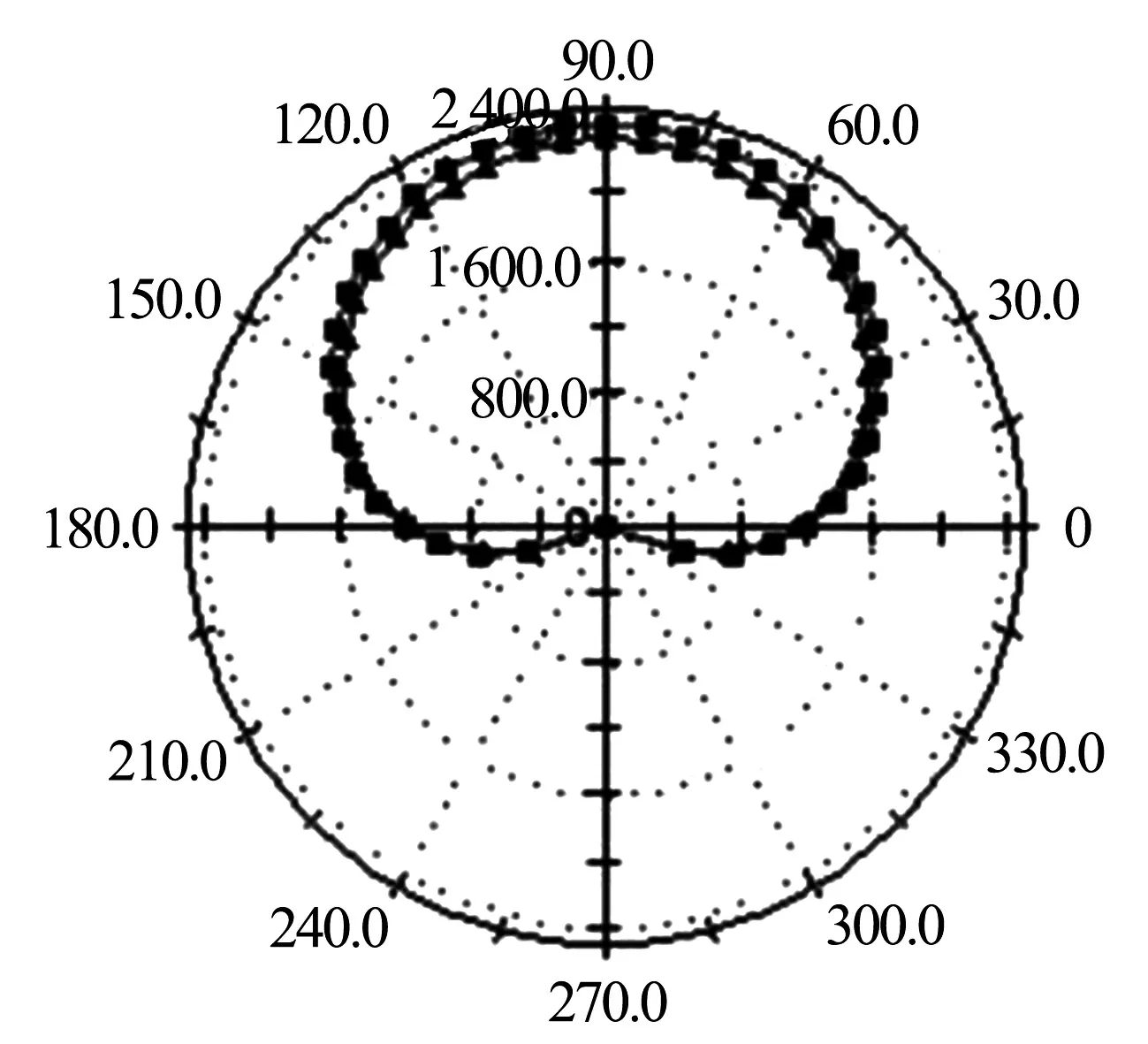
方案D双列调心滚子轴承内外圈滚道载荷分布雷达图如图6所示，该轴承第一列共有36个滚动体受载，位置分布在-18°～98°；第二列共有22个滚动体受载，位置分布在24°～156°.两列滚动体最大受载位置均在90°处，分别为第一列24 420 N，第二列10 580 N.从滚道载荷仿真结果看，调心滚子的两列受载并不均匀，第一列受到径向载荷为-383 000 N，轴向载荷为-68 700 N；第二列受到径向载荷为131 000 N，轴向载荷为18 500 N.

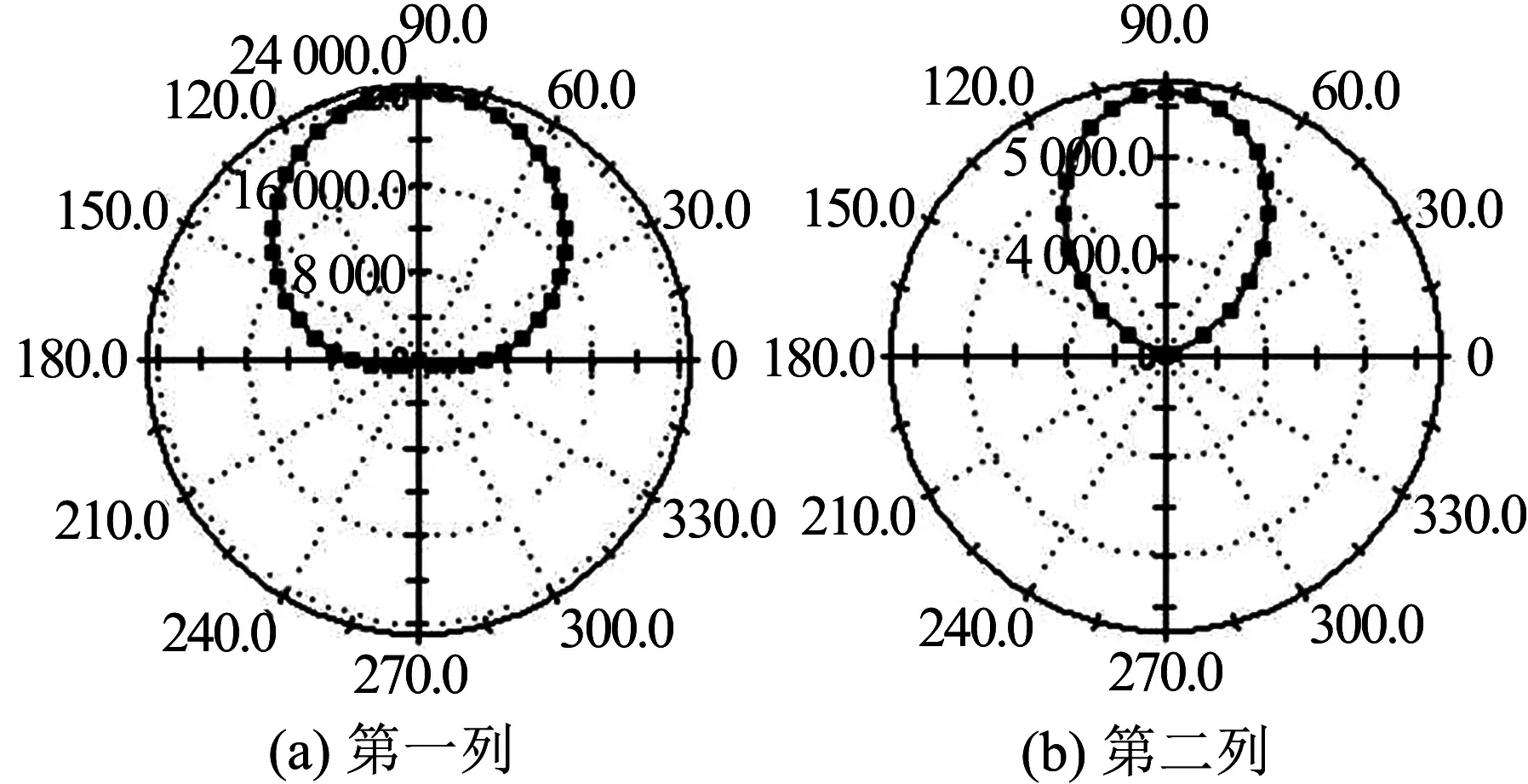
图6 方案D双列调心滚子轴承内外圈滚道载荷分布

产生这种两列不均匀受力的主要原因有两个：一是由于两列调心滚子具有7.125°的接触角，且两列调心滚子是面对面布置.外载荷中有很大的径向载荷，导致轴产生一定的弯曲变形，而球面滚子具有调心能力，第一列轴承内圈受力部分向轴承外旋转，接触角增大，在径向力的作用下产生更大的轴向派生力，且力的方向指向轴的右端.那么第一列的滚子有相对更强的向轴承外部移动的倾向，滚子与滚道的接触条件相对变差.第二列轴承内圈受力部分向轴承中心旋转，接触角减小，轴向派生力相对较小，获得相比于第一列更加宽松的接触条件.二是由于外载荷中有相对较大的指向轴左端的轴向载荷，双列调心滚子轴承内圈有大约119.30 μm的轴向位移，导致面对面布置的圆锥滚子轴承必定有一个被压紧一个被放松，从而导致第一列的调心滚子被轴向压缩，第二列则轴向放松；所以双列调心滚子轴承受载不均匀，且第一列受力要比第二列大.

下面分析经过修形后受力大的第一列调心滚子与套圈的接触应力.图7(a)、7(b)、7(c)分别是第一列调心滚子与内套圈的最大接触应力的雷达图、接触应力云图和沿滚子轴向接触线上的最大应力分布曲线图.由图7(a)可知，方案D双列调心滚子轴承第一列最大接触应力分布为较为圆滑的心形，没有出现修形前急剧增大的情况.所有滚动体均没有出现超过屈服极限的情况.接触应力最大的滚动体同样出现在90°处，大小为2 410.11 MPa.由图7(b)可以看出各个滚动体的接触应力在轴承周向以角位置90°为中心，向两侧递减至零；由图7(c)可知，在滚动体接触线上，接触应力呈现中间高两侧低的弧形，以接触线中点为中心向两侧递减至零，接触状态均匀.

(a) 最大滚道接触应力分布

3 结论

根据该型悬臂式掘进机的实际工作条件，对四种方案主轴系统进行了全面的分析，包括主轴的应力和变形、各轴承整体受力以及轴承滚道载荷分布和接触分布应力的详细分析，可以发现，使用双列调心滚子轴承的方案C和方案D要明显优于使用双列四点接触球轴承的方案A和方案B.但调心滚子轴承边缘应力集中现象严重，在进行调心滚子对数修形优化后，虽然滚子中部区域的接触应力有所增加，但消除了边缘效应的不利影响.方案C和方案D两者仅是圆锥滚子轴承的安装方式不同，对轴承的最大接触应力的影响很小.考虑到方案D的轴承布置方式对轴的弯曲变形程度影响更小，同时轴承的安装与拆卸也较为方便，所以方案D为最优轴承布置方案.

另外，除了对调心滚子进行对数修形外，还可以通过优化调心滚子的曲率半径来消除调心滚子轴承的边缘效应，这个问题将另文进行介绍.