镁合金车体车顶边梁型材优化

臧兰兰，阎帅，李文斌，时森，曲晓梅，初彦彬，陈秉智

(1.中车大连机车车辆有限公司 城铁开发部，辽宁 大连 116028；2.大连交通大学 机械工程学院，辽宁 大连 116028；3.大连交通大学 机车车辆工程学院，辽宁 大连 116028)

镁合金列车侧顶是连接列车侧墙和顶棚的关键结构，不仅承载着列车顶棚的设备，而且对列车的安全行驶具有重要意义.侧顶由镁合金作为原材料采用挤压成型工艺而成，镁合金具有密度低，比强度和比刚度高等优良特性，密度为1.8 g/cm3，约为铝合金的2/3，镁合金弹性模量为45 000 MPa，约为铝合金的63%，镁合金泊松比为0.33.因此，在实现镁合金车体轻量化的同时，车体的性能也面临挑战.

结构优化是优化列车侧顶性能的主要方式，主要包括拓扑优化、尺寸优化、形状优化等方法，其中拓扑优化属于概念设计阶段，尺寸优化和形状优化属于详细设计阶段[1].目前，众多学者从多学科领域对结构优化提出了不同的结构优化方案.佟维等[2]联合拓扑优化、形状优化和挤压型材截面为一体的协同优化方法，在铝合金车体侧顶挤压型材配置垂直型筋板和斜向角度型筋板，提出了一种渐进结构优化方法，基于有限元软件Marc系统编写了优化程序，并应用于工程实例.赵士忠等[3]以新型高速列车侧顶为优化对象，在均布压力作用下，对车体侧顶气密工况进行分析，对侧顶型材和型材之间相互连接处的结构进行优化，侧顶的应力降幅明显.付世欣等[4]对矩形带孔支撑板进行形状优化，在孔附近的最大应力不仅明显降低，而且支撑板的质量降低了约27%，显著提高了结构的强度.杜宪峰等[5]将拓扑优化和形状优化两者相结合，在满足刚度和强度的条件下，提高了各阶模态频率，降低了振动烈度.刘高君等[6]采用拓扑优化和尺寸优化组合优化的方法，在满足强度的同时，减重效果明显.谭惠日等[7]基于变密度法，对内燃机排障器进行拓扑和尺寸优化，最大应力值降幅明显.

本文采用子模型进行优化设计，降低计算规模的同时保证了结构设计合理边界，在列车侧顶已有筋板分布基础上，将尺寸优化和形状优化联合，对列车侧顶的筋板设计分布提供了有益参考.

1 有限元分析

1.1 侧顶有限元建模

列车侧顶几何模型如图1所示，型材Ⅰ和型材Ⅱ是通过焊接连接而成，本文主要对型材Ⅰ进行结构优化分析.

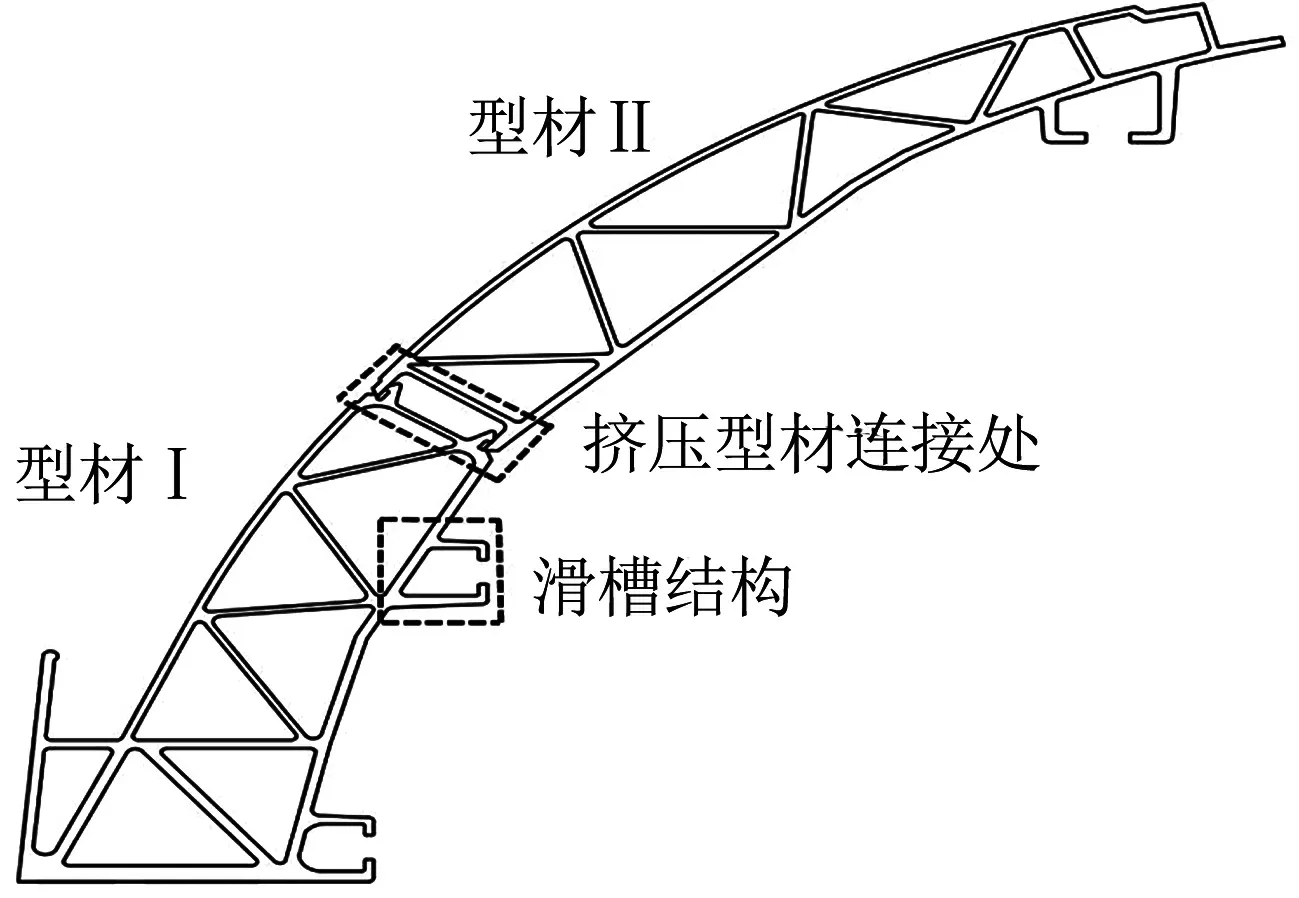
图1 侧顶几何模型

在垂载AW3工况下，通过hypermesh建立车体有限元模型，离散后整车节点总数为2 398 025，单元总数为2 957 558，其中型材Ⅰ节点总数为120 128，单元总数为135 279，重量为0.403 9 t，采用四节点壳单元.型材Ⅰ有限元模型如图2，筋板①、②、③、④、⑤厚度分别为3、2.5、4、4.5、8 mm.

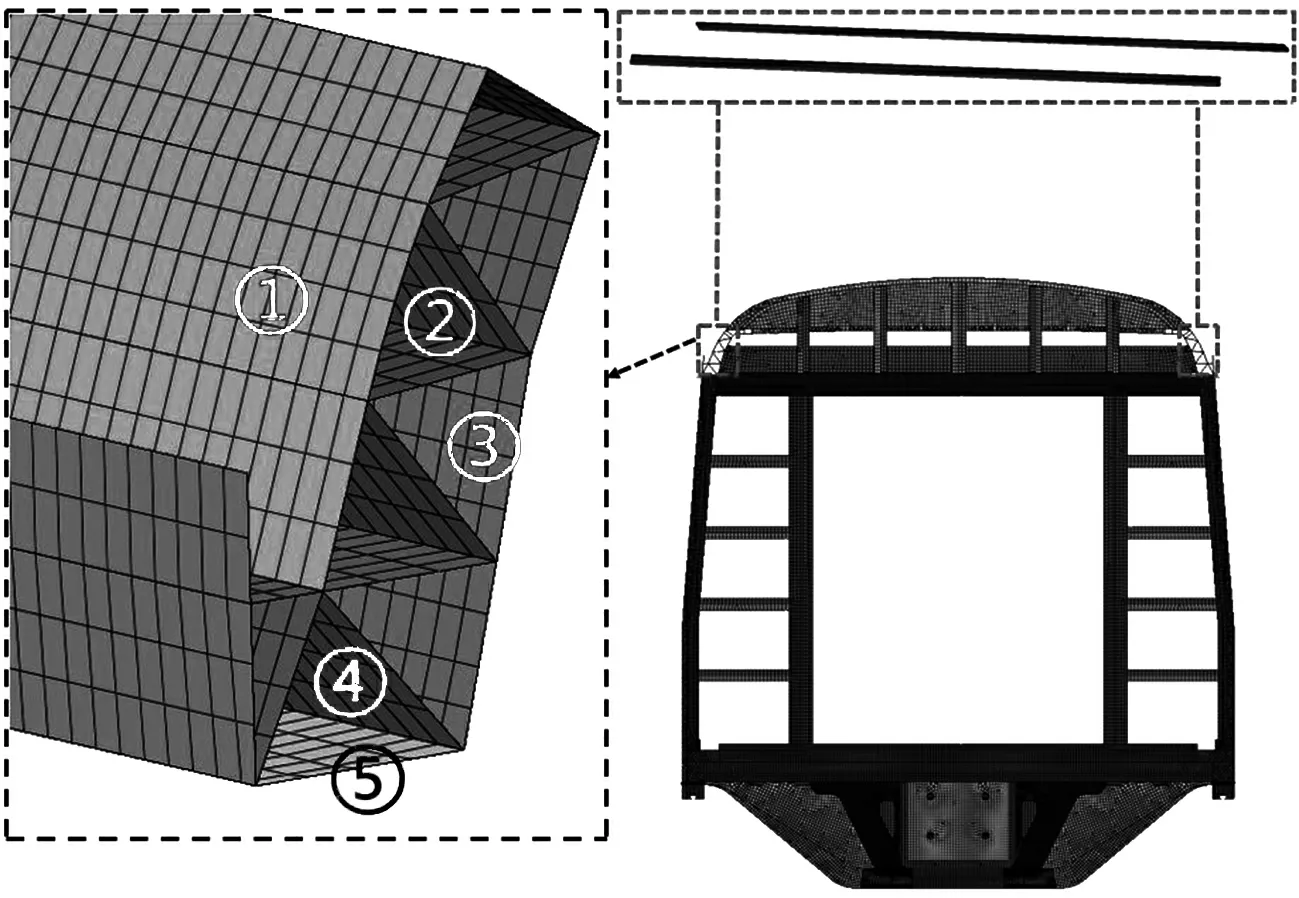
图2 侧顶有限元模型

1.2 子模型分析

车顶型材Ⅰ网格数占整车4.57%，采用整车模型对侧顶结构进行优化，计算时间成本高.对侧顶结构进行子模型建模降低计算量非常必要.车体有限元静力学问题是一个线性方程组求解问题:

[K]{δ}={F}

(1)

式中，[K]为结构的总刚度矩阵,{δ}为节点的位移向量，{F}是单元节点的外载荷向量.

假设δ1为子模型外部节点位移向量的已知量，δ2为子模型节点位移向量的未知量，则式(1)可展开为：

(2)

以切割位移作为边界条件，截取侧顶挠度在整车中下降幅度最大的部分，选取的侧顶部分以靠近整车端墙的部分作为距离起始点，分别选取切割边界后的4条轮廓线，如图3和图4.

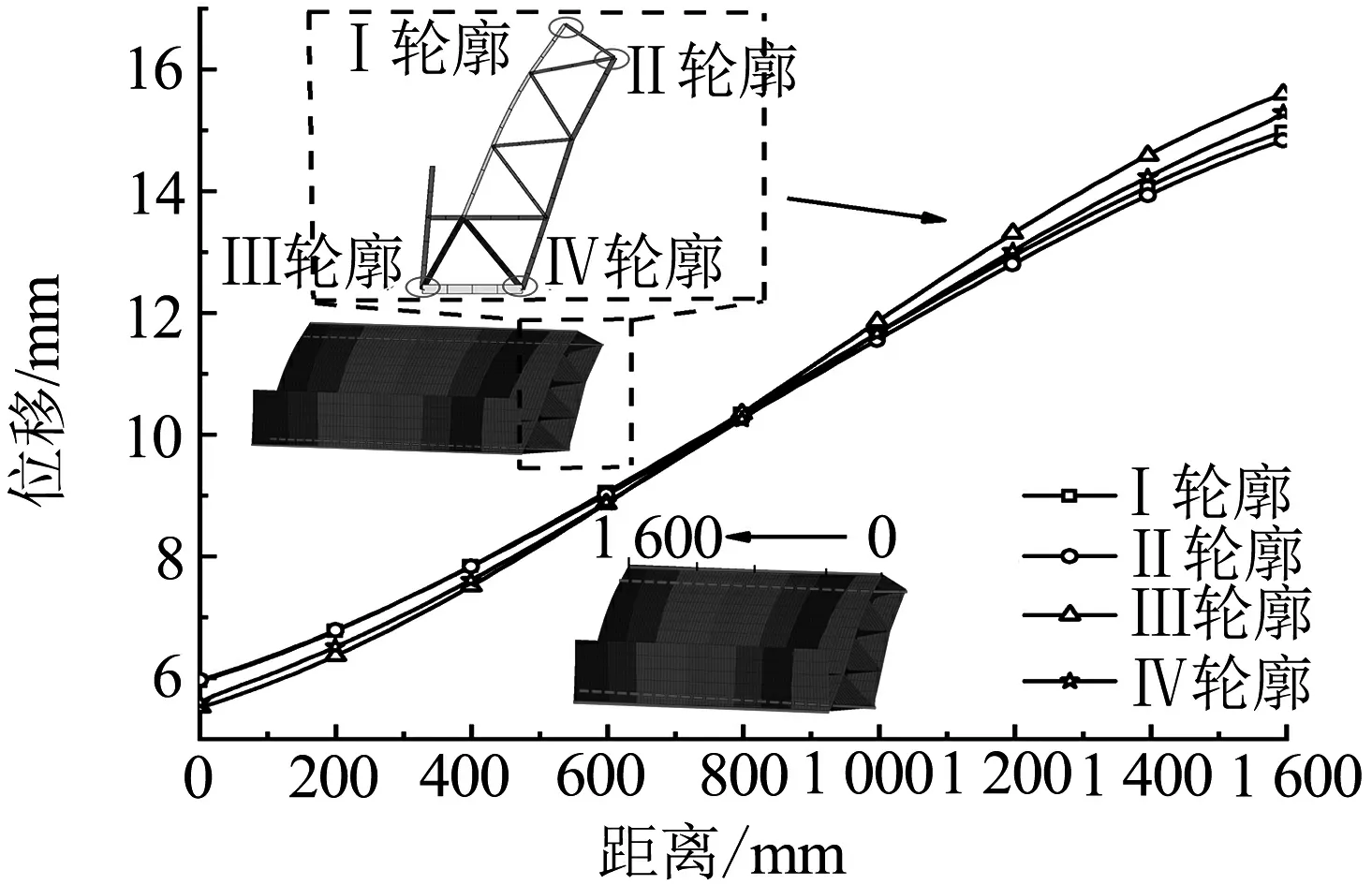
图3 子模型位移

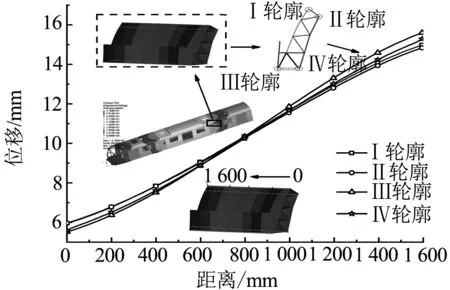
图4 子模型所在的整车模型位移

对比子模型和整体模型时发现，位移趋势线图以及同位置处的位移差异很小，切割后子模型的准确性得到验证.后续尺寸优化以及形状优化均基于子模型进行优化分析.

2 尺寸优化

2.1 灵敏度分析基本理论

灵敏度分析是结构性能参数对设计变量变化的敏感性，能够反映出各设计变量对结构性能影响程度，能够给设计者提供设计建议，进一步优化结构性能，灵敏度分析其数学含义可以理解为结构性能参数对设计变量的变化梯度[8]，其表达式为：

(3)

车体结构在静态作用下，有限元方程形式为式(1)，方程两侧对设计变量xi求导数，可表达为：

(4)

则

(5)

∂{δ}/∂xi为节点位移对设计变量xi的灵敏度.

2.2 侧顶静态灵敏度分析

为了进一步提高截面抗弯性能，在原始镁合金结构端面上进行了腔体扩展，新型侧顶几何模型如图5.

图5 新型侧顶几何模型

基于新型侧顶在整车中进行有限元网格划分，进行整车静强度分析，读取整车模型结果文件，提取切割边界上的节点强制位移作为子模型的边界条件[9].进行子模型静强度分析，位移结果如图6.

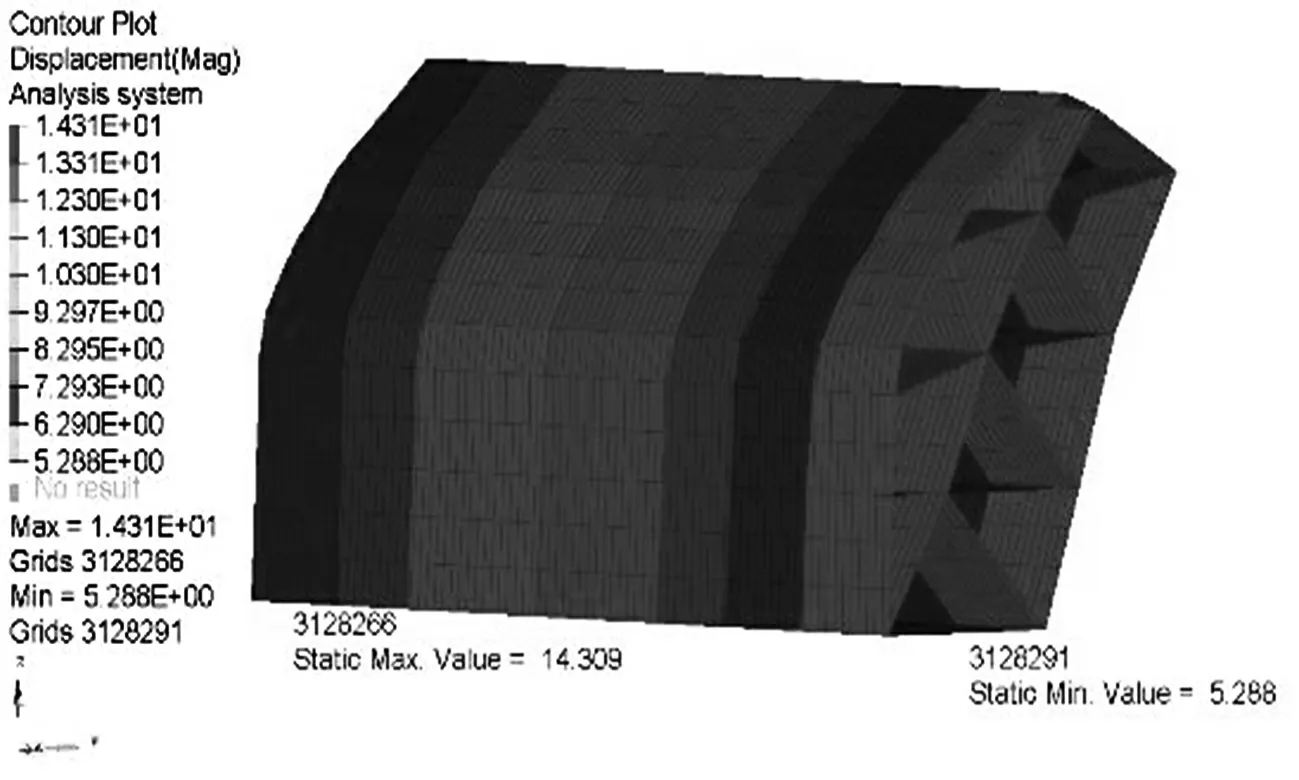
图6 新型侧顶位移结果

基于子模型位移结果云图，分析了包含型腔件和型材Ⅰ在内的新型侧顶等26个结构件(表1)的厚度变化对最大位移敏感度分析.其中，T1～T8是加入型腔件之后的筋板，T9～T26是原始侧顶型材Ⅰ的筋板.

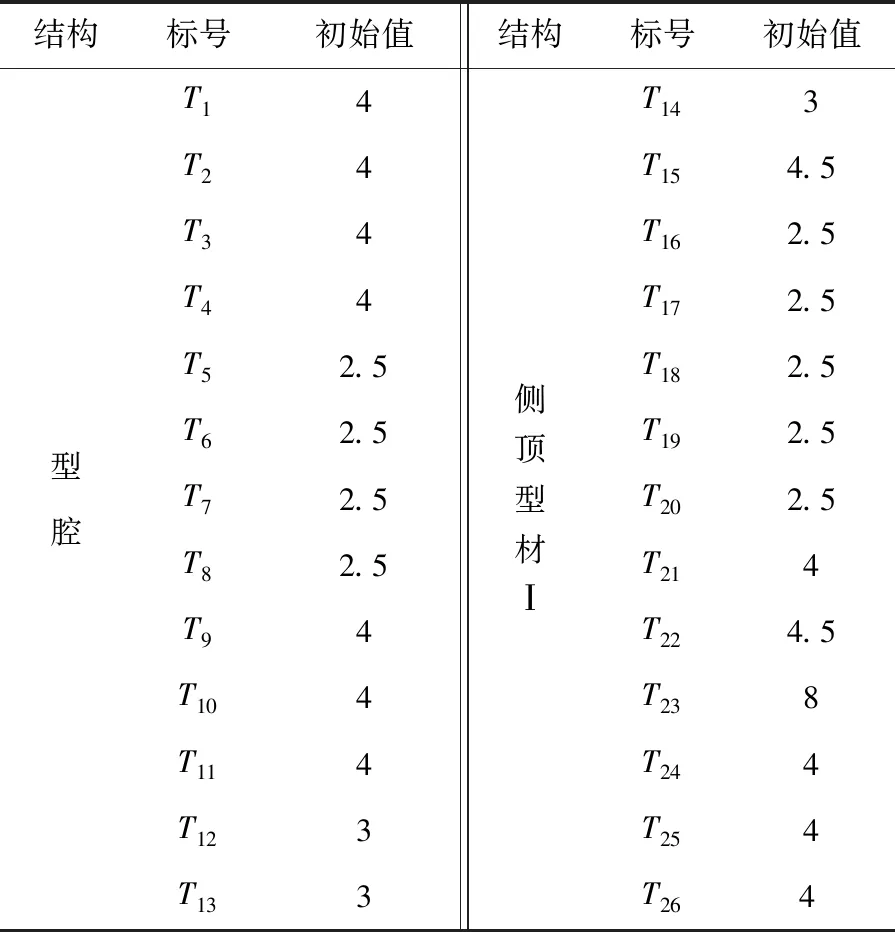
表1 构件厚度参数 mm

从图6分析得知，子模型中最大的合成位移为14.309 mm.首先，将最大合成位移的节点所在整个截面的节点进行截取，共计71个节点.其次，将这71个节点的位移分别对表1构件厚度参数的26块筋板灵敏度进行灵敏度分析.最后，将这71个节点的灵敏度分析值进行同等权重相加求和.这种方式可以简单理解为最大位移节点所在的整个截面对26个构件进行灵敏度分析，如图7，这是一种权衡所有筋板的体现，这种分析方式避免了最大位移点只对周围部分筋板敏感，而对较远处筋板分析较弱的现象，但较远处的筋板对于型材与型材之间的连接，车顶重量的分担等也很重要.

图7 节点位移灵敏度

虽然通过传统灵敏度的分析，能够得知该车体的性能参数对各设计变量影响程度的大小，但是各设计变量发生变化时，车体性能参数不仅会发生变化，而且所参考的设计约束条件比如质量等参数也会发生变化.侧顶质量是本文所关注的结构性能参数，侧顶质量对各构件变量灵敏度如图8.

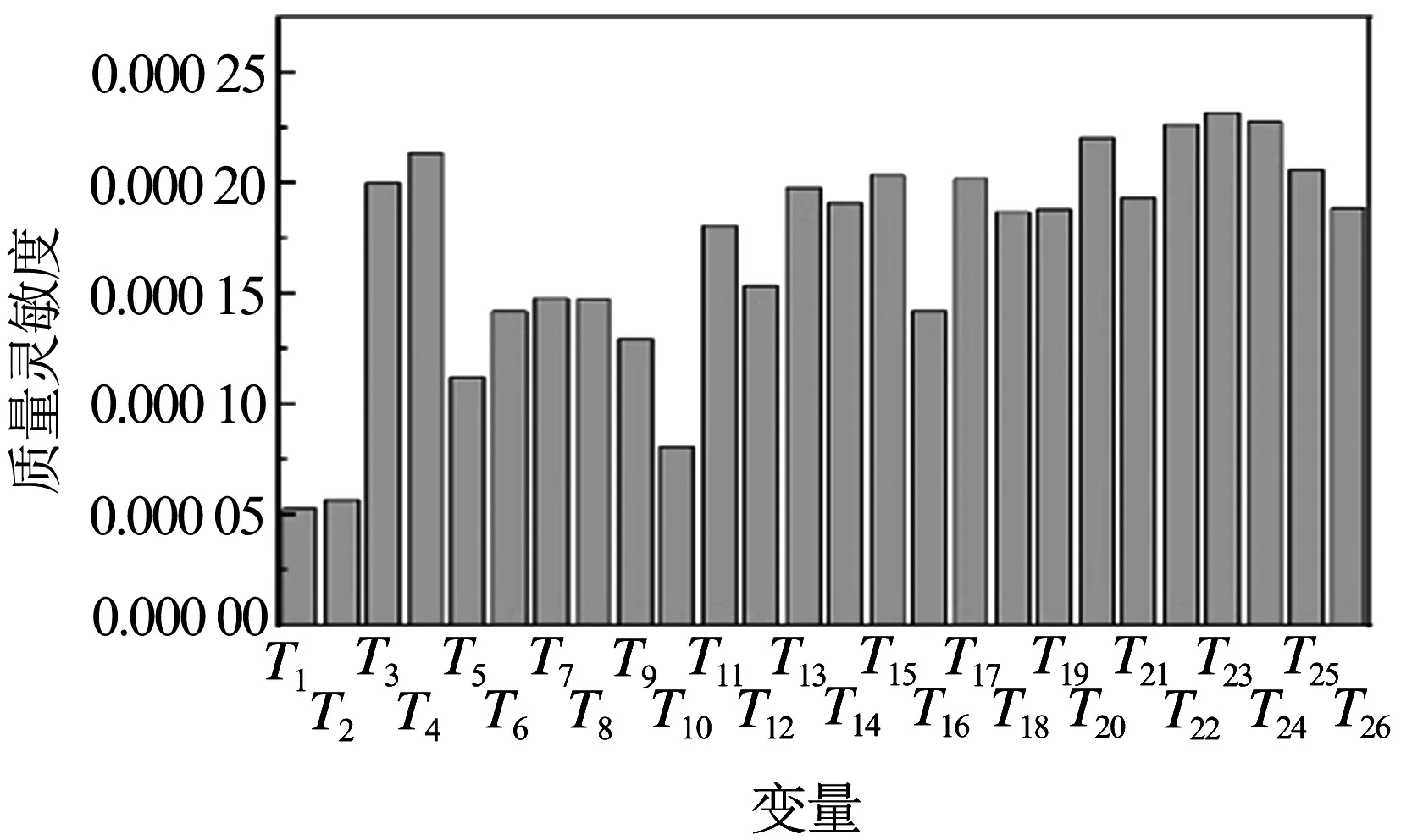
图8 质量灵敏度

侧顶不同筋板构件对位移和质量影响不同，其中灵敏度值的正负表示设计变量对结构性能参数的不同影响.当灵敏度值为正时，表示设计变量的变化方向与结构性能参数相同；当灵敏度值为负时，表示设计变量的变化方向与结构性能参数相反；当灵敏度值为0时，表示该设计变量对结构性能参数影响值为0，即没有影响.灵敏度绝对值的大小表示该设计变量对结构性能参数影响的快慢.

为避免盲目选取设计变量，提高设计效率，因此有必要将两者的灵敏度结合起来进行分析[10].侧顶性能参数位移灵敏度S与侧顶质量灵敏度Sm的比值S/Sm称为位移对质量的相对灵敏度.依据图9相对灵敏度可以给设计者提供设计方案.

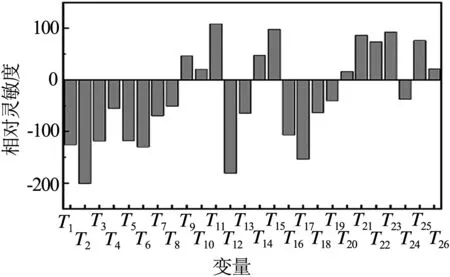
图9 相对灵敏度

由相对灵敏度数值可把变量分为四类：

第一类设计变量：T1，T2，T3，T5，T6，T12，T16，T17，这类设计变量的相对灵敏度值为负值，表示设计变量与结构性能参数趋势相反，即最大节点的位移随着这些板的厚度增大而减小，减小而增大，并且绝对值较大.板厚轻微改变，就会引起位移较大变化，结合工艺要求，设计变量厚度上下限值为初始板厚的70%至最大板厚10 mm.

第二类设计变量：T4，T7，T8，T13，T18，这类设计变量的相对灵敏度值为负值，绝对值略大，表示最大节点的位移随着这些板的厚度增大而减小，减小而增大，并且幅度值较大.板厚的改变，就会引起位移的变化，设计变量厚度上下限值为初始板厚的70%至最大板厚8 mm.

第三类设计变量：T11，这类设计变量的相对灵敏度值为正值，表示设计变量与结构性能参数趋势相同，值较大，表示最大节点的位移随着这些板的厚度增大而增大，减小而减小，并且幅度值较大.板的厚度轻微的改变，就会引起位移的变化，设计初衷希望这类板较薄一些，即位移会小一些.设计变量厚度变化范围为初始板厚的±30%.

第四类设计变量：T15，T21，T22，T23，T25，这类设计变量的相对灵敏度值为正值，值略大，表示最大节点的位移随着这些板的厚度增大而增大，减小而减小，并且幅度值较大.板的厚度轻微的改变，就会引起位移的变化.设计变量厚度的变化范围为初始板厚的±20%.

2.3 新型侧顶尺寸优化

经过灵敏度分析后设计变量由初始的26个缩减至19个，以最小位移为目标函数对其进行尺寸优化，具体优化模型为：

(6)

式中，xi为尺寸优化的第i个设计变量的厚度，Usize为尺寸优化过程中节点位移.xk，xh为设计变量厚度的上下限，massxi为第i个设计变量的质量，mass0为尺寸优化前侧顶的质量.

2.4 尺寸优化结果分析

由新型侧顶子模型经过2次迭代后函数收敛，优化过程结束，优化结果见表2，同时将新型侧顶子模型得到的每一步迭代设计变量值，均在整车模型中进行验证，迭代曲线如图10.由迭代结果知，随着子模型迭代次数增加，子模型所在的整车模型位移下降明显，由初始的14.151 mm下降至13.37 mm，位移降幅0.781 mm.

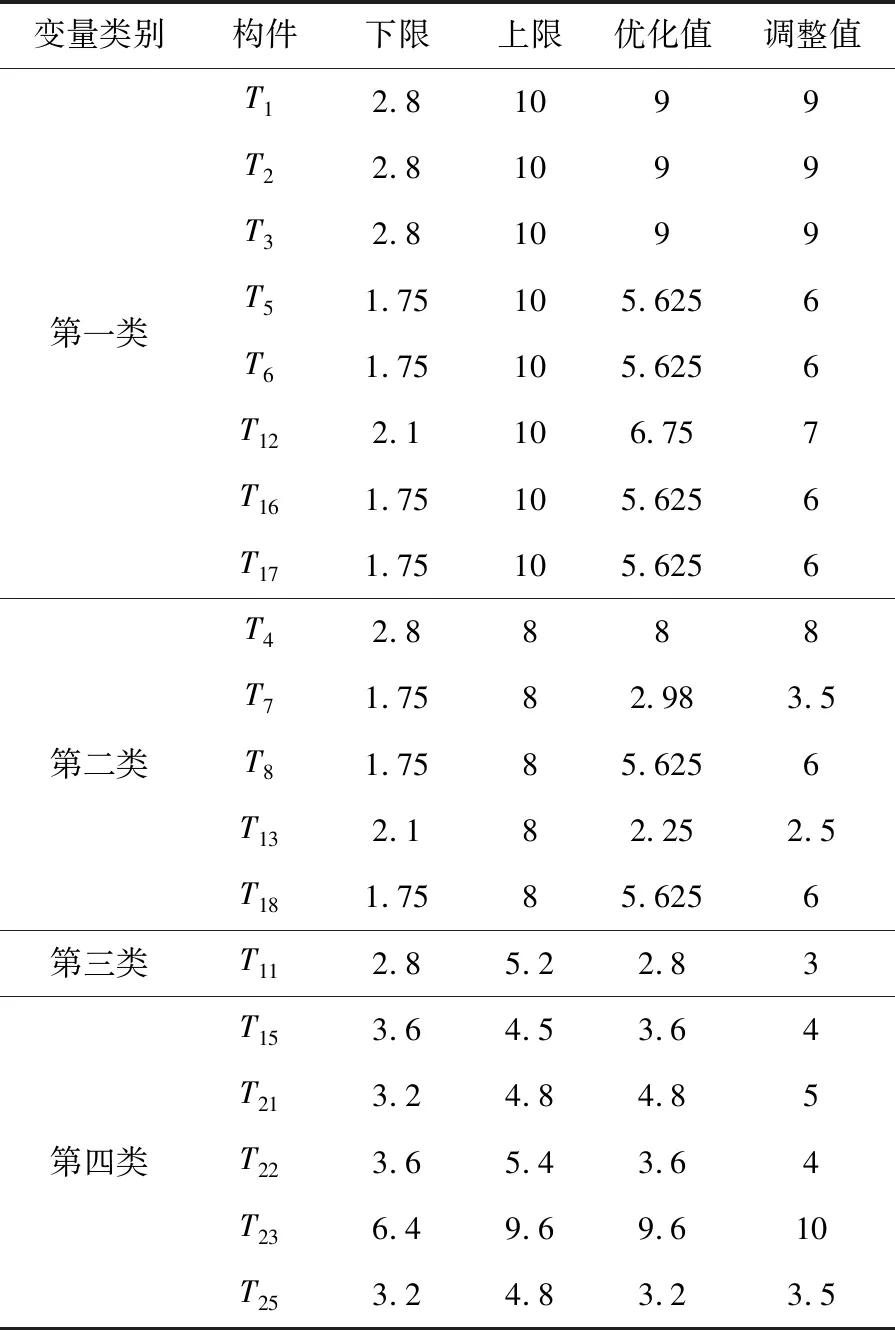
表2 设计变量参数表

图10 优化迭代过程

3 形状优化

3.1 优化模型

形状优化是把已有的有限元模型，通过不断改变网格节点的位置，在满足体积、应力等一些约束条件下，最大限度地满足增加刚度、位移等一些目标要求.

网格变形技术是形状优化过程中的关键步骤，其过程包含创建Domains(域)和Handles(控制柄)，如图11，通过移动控制柄控制网格变形点的范围，结合工艺制造，在型材连接处位置设置其变形点，共计9个变形点，9个变形点分别在x，y向变化的范围是±15 mm.

建立以位移最小为优化目标，以局部应力和质量为约束，以形状为设计变量的优化模型，其表达式可为：

(7)

minUshape

式中，P为形状优化设计变量矩阵，即局部区域形状摄动，Ushape为形状优化过程中的节点位移，pl，pv为设计变量取值的上下限值，可理解为图10中x，y向变化范围，masssize为尺寸优化后侧顶的质量.

3.2 结果分析

形状优化经过两次迭代后，在两次目标函数值容差范围0.005 mm内，函数收敛，如图12，在变化范围内形状最终确定.

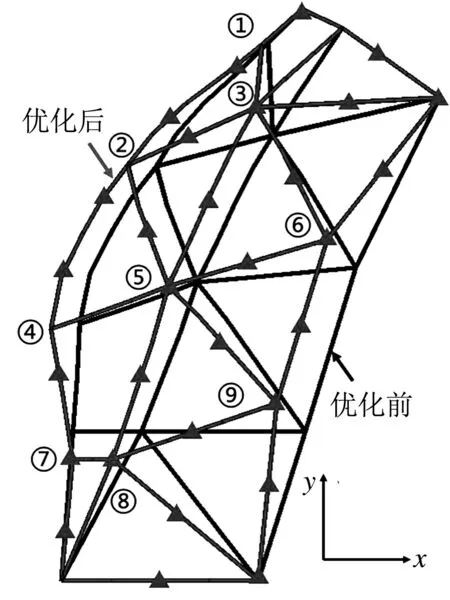
图12 形状优化结果

以每个优化前的新型侧顶控制柄为坐标原点，经过形状优化后新型侧顶优化前的点与优化后的点移动如表3.

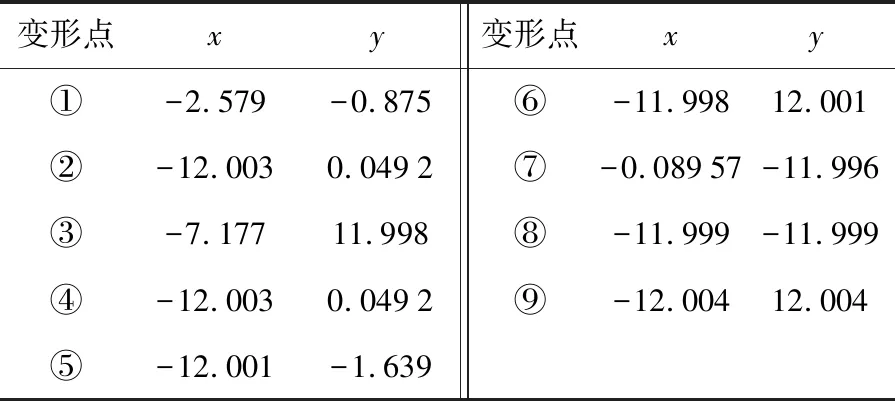
表3 变形点位移

由变形点移动方向和距离可知，在x，y约束的范围内(±15 mm)达到了最优解.

3.3 整车验证结果

原始侧顶质量为0.403 9 t，加型腔后的新型侧顶质量为0.435 5 t，尺寸优化后质量为0.582 8 t，经过形状优化后质量为0.581 9 t.

将每步优化过程在整车里进行验证，同时仅显示侧顶部分，由图13可知，应力经过每次优化后均有所下降，其中经过形状优化，应力下降最为明显.由图14可知，在形状优化之前，每次优化垂向位移下降大致相同，经过形状优化，垂向位移下降幅度较小，但侧顶质量有所减轻.

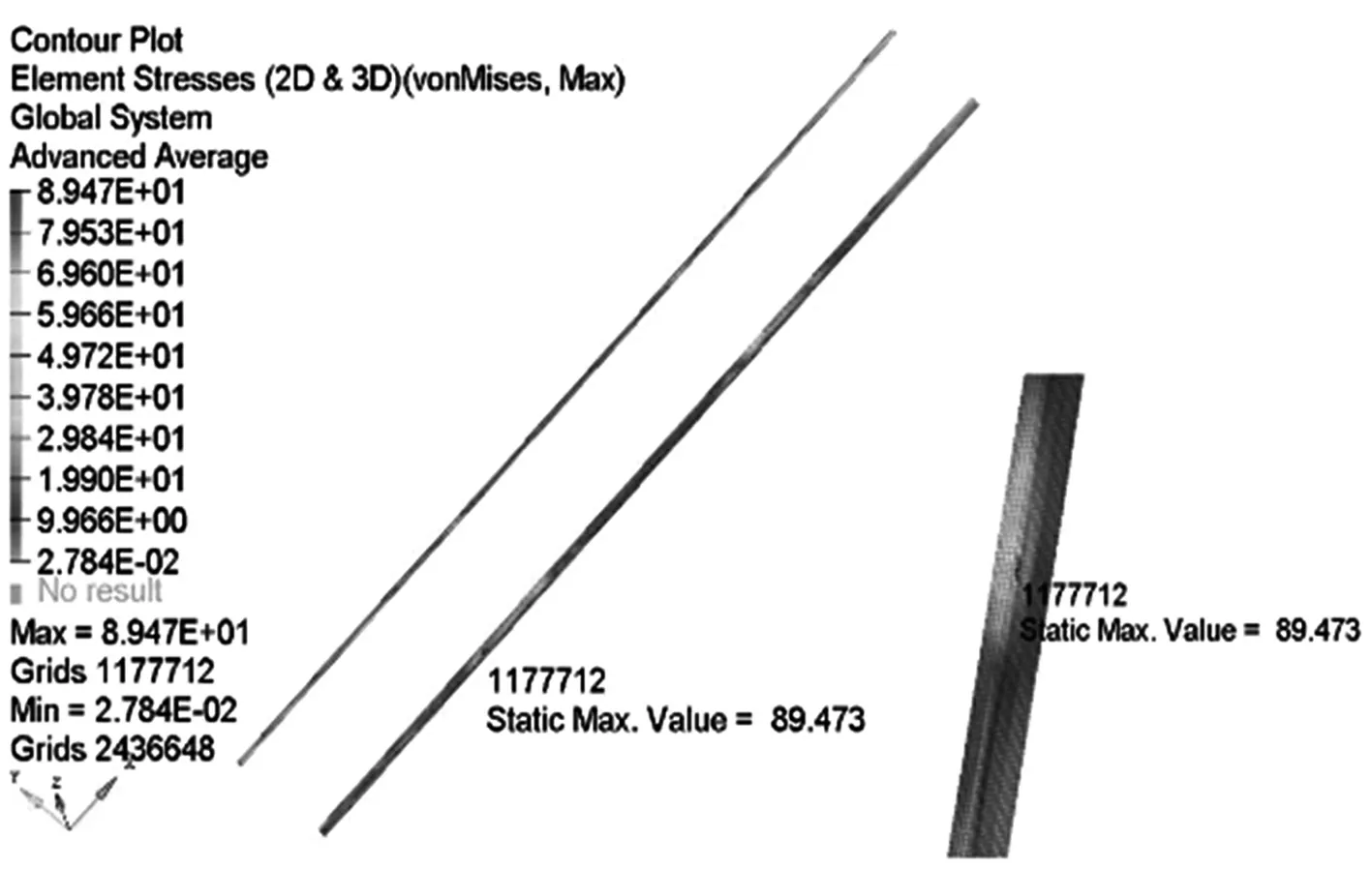
(a) 原始侧顶

(a) 原始侧顶

4 结论

本文以侧顶为研究对象，进行有限元强度分析，提取侧顶子模型边界条件，进行子模型与子模型所在的整体模型位移对比，位移差别较小，验证了子模型的可行性，为后续优化节省了计算时间.结果表明：侧顶经过尺寸和形状的两级优化后，在整车进行验证，侧顶最大应力由89.473 MPa降为61.057 MPa，下降31.76%；侧顶的垂向位移由初始的17.347 mm降至15.493 mm，下降10.69%.