基于Wiedemann74跟驰模型的VISSIM排放测算适用性分析

杨钰浩，于谦

(1.陕西铁路工程职业技术学院，陕西 渭南 714000；2.长安大学 运输工程学院，陕西 西安 710064)

将微观交通仿真软件与排放模型结合，分析交通管理策略对机动车排放的影响，已经成为交通环境领域的一个研究热点.VISSIM作为常用的微观交通仿真软件，其内置的Wiedemann74生理心理模型用来刻画跟驰后车不同状态下的瞬时速度与加速度.国内外众多学者利用VISSIM开展了多项微观交通仿真及排放研究[1-3].在以往的微观仿真研究中，VISSIM仿真在进行参数标定时，较多选取交通流量、平均速度、车头时距、排队长度、加减速度等指标[4-5].Arafat等[6]基于现实交叉口数据，以平均车头时距为评价标准，建立路网仿真，校准车头视距相关模型参数.Faezi 等[7]采用描述性统计和推论统计的方法，以期望速度和起步加速度为校准参数，研究不同气候条件下，交叉口交通饱和流量状况.Siam等[8]基于实测高速公路数据，采用模拟退火算法，以仿真和实测车辆逐秒速度为评价标准，以Wiedemann99跟驰模型参数为校准参数，提出一种基于VISSIM微观仿真的自动化参数校准工具.Eric等[9]基于实测视频数据，以交通流量、平均排队长度和最大排队长度为评价标准，以最小车头时距和车辆速度为校准参数，建立路网仿真，研究在无信号的 T 形交叉口处引导左转车道安装的必要性.齐泽阳等[10]基于实测有轨电车数据，并以VISSIM进行路网仿真.以行程时间为评价指标，以VISSIM中的跟驰模型参数和换道模型参数为校准参数，提出了一种参数敏感性分析流程.屈新明[11]等人通过校准跟驰模型核心参数，选取交叉口信号车头时距作为检验标准，提高了仿真评价的可信度.

机动车比功率(Vehicle Specific Power，VSP)定义为单位质量机动车发出的功率，主要与车辆瞬时速度和加速度有关，相关研究表明机动车比功率与车辆尾气排放之间存在着明确的物理意义和数学关系[12].传统标定方法未选取VSP分布、车辆加速度分布等微观指标，同时对VISSIM中驾驶员微观驾驶行为刻画及其对排放计算结果影响等微观层面研究较少，往往交通排放仿真结果与实际情况差异较大，所以在排放仿真过程中需要进一步对相关驾驶行为参数进行标定.

基于此研究背景，本文从VISSIM内置的Wiedemann74跟驰模型研究出发，在收集西安市城市道路轻型车跟驰驾驶行为数据的基础上，对比实测和仿真VSP分布情况，并结合实际情况对仿真参数进行优化，分析VISSIM排放测算适用性.

1 实测跟驰数据采集

本文在西安市分别选取二环路、子午大道全段(快速路)、长安路的航天城到钟楼路段(主干路)、自强路全段(次干路)、东七路全段(支路)进行跟车试验，试验路段如图1所示.测试车辆选取一辆轻型汽油车，车型为福特福克斯，驾驶员驾龄为3年.数据收集采用Hi-drive跟驰数据采集仪器，如图2所示.为保证数据的全面性，采用三天分别获取其高峰状态(两天)和平峰状态(一天)，测试时间节点如表1所示.

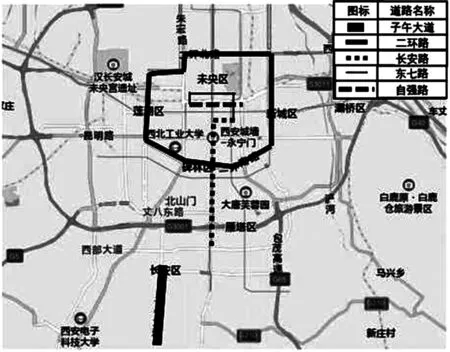
图1 跟驰数据采集行车路线图

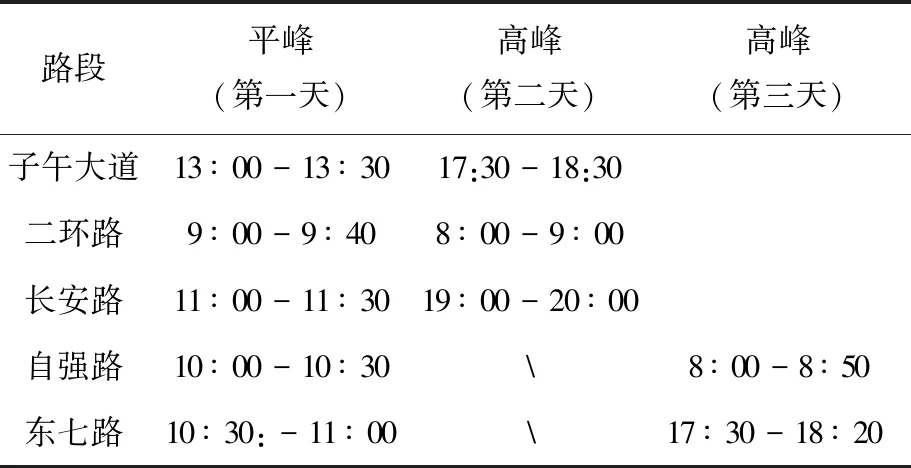
表1 跟驰数据采集时间节点表

图2为跟驰数据采集设备的Hi-driver示意图，跟驰后车配置Hi-driver仪器，其内置GPS获取跟驰后车瞬时速度；前置激光获取跟驰前车瞬时速度；前置雷达获取跟驰前后车车辆间距.

图2 跟驰数据采集设备Hi-driver示意图

跟车测试因Hi-driver设备在遇到隧道或立交桥时受信号干扰可能会导致本车速度缺失，因此本文对数据丢失在5 s以内的速度和加速度采用线性插法进行补全.而大于5 s的数据丢失，则将其作为前后两段数据的分界点；本次测试路段较为平坦，由于车辆油耗、排放受道路坡度影响较大，因此对少数道路坡度较大的路段数据予以剔除.

根据测试车型及测试环境，本文在计算车辆比功率时，采用下列公式[13]计算VSP：

VSP=v(1.1a+0.132)+0.000 302v3

(1)

∀VSP∈[n-0.5,n+0.5]VSPbin=n

(2)

其中，VSP代表车辆逐秒比功率，kW/t；v代表车辆行驶速度，m/s；a代表车辆行驶瞬时加速度，m/s2；n为整数.

2 模型仿真思路

Wiedemann74跟驰模型是一种基于驾驶员生理心理的跟驰模型，根据前后车距离和速度差将后车行驶状态划分为自由行驶、逼近行驶、跟驰行驶和制动行驶四个状态.根据后车的行驶状态，计算后车加速度，跟驰后车加减速度计算思路如图3所示.在基于Wiedemann74跟驰模型进行后车速度、加减速度计算时，模型中各参数意义及默认取值如表2所示[14-15].

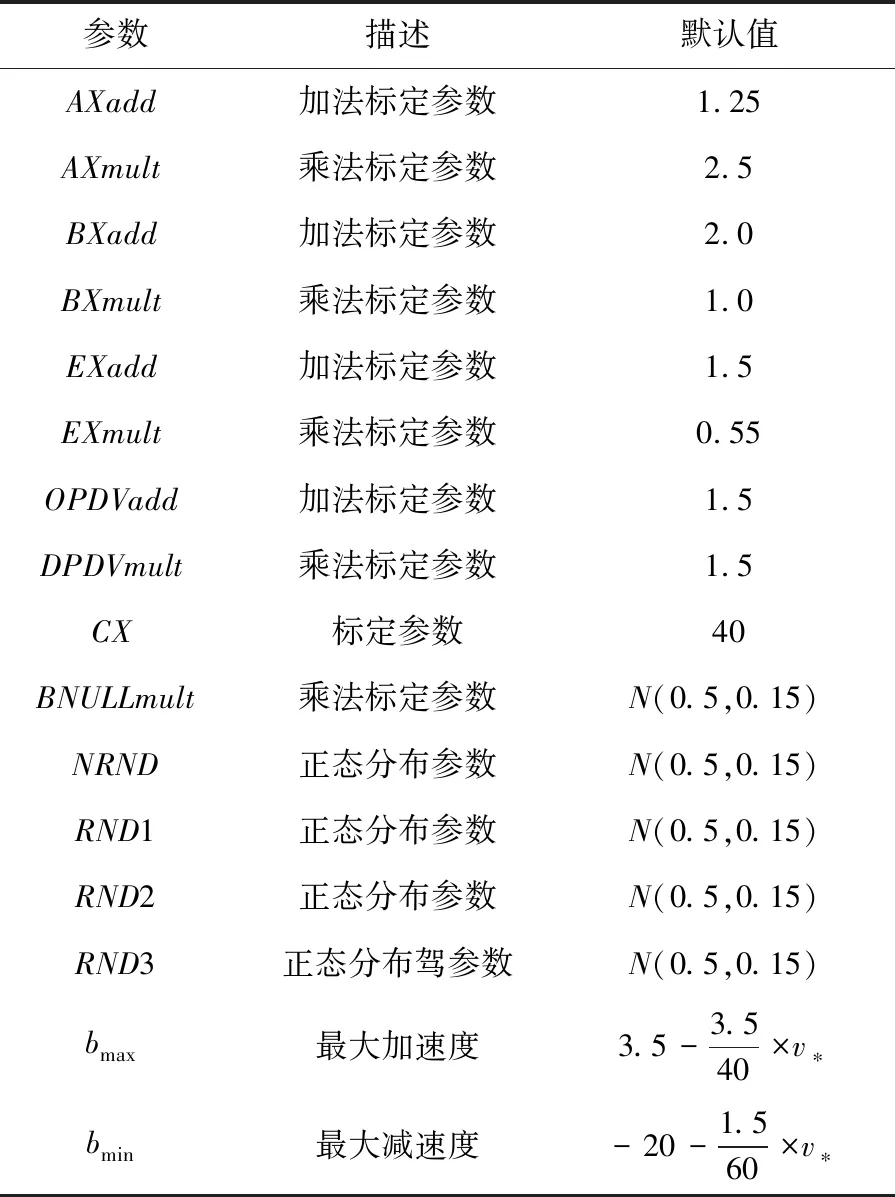
表2 Wiedeman74跟驰模型参数默认取值

如图3所示，跟驰后车的加减速度根据前后车间距和前后车速度进行计算，首先确定在当前时刻后车处于哪种行驶状态，再根据各个行驶状态不同的加减速度计算方式，确定当前后车的加速度，从而确定下一秒跟驰车辆的速度.本文通过python编程实现跟驰模型，根据实测前车的数据，循环输出跟驰后车的速度和加速度.

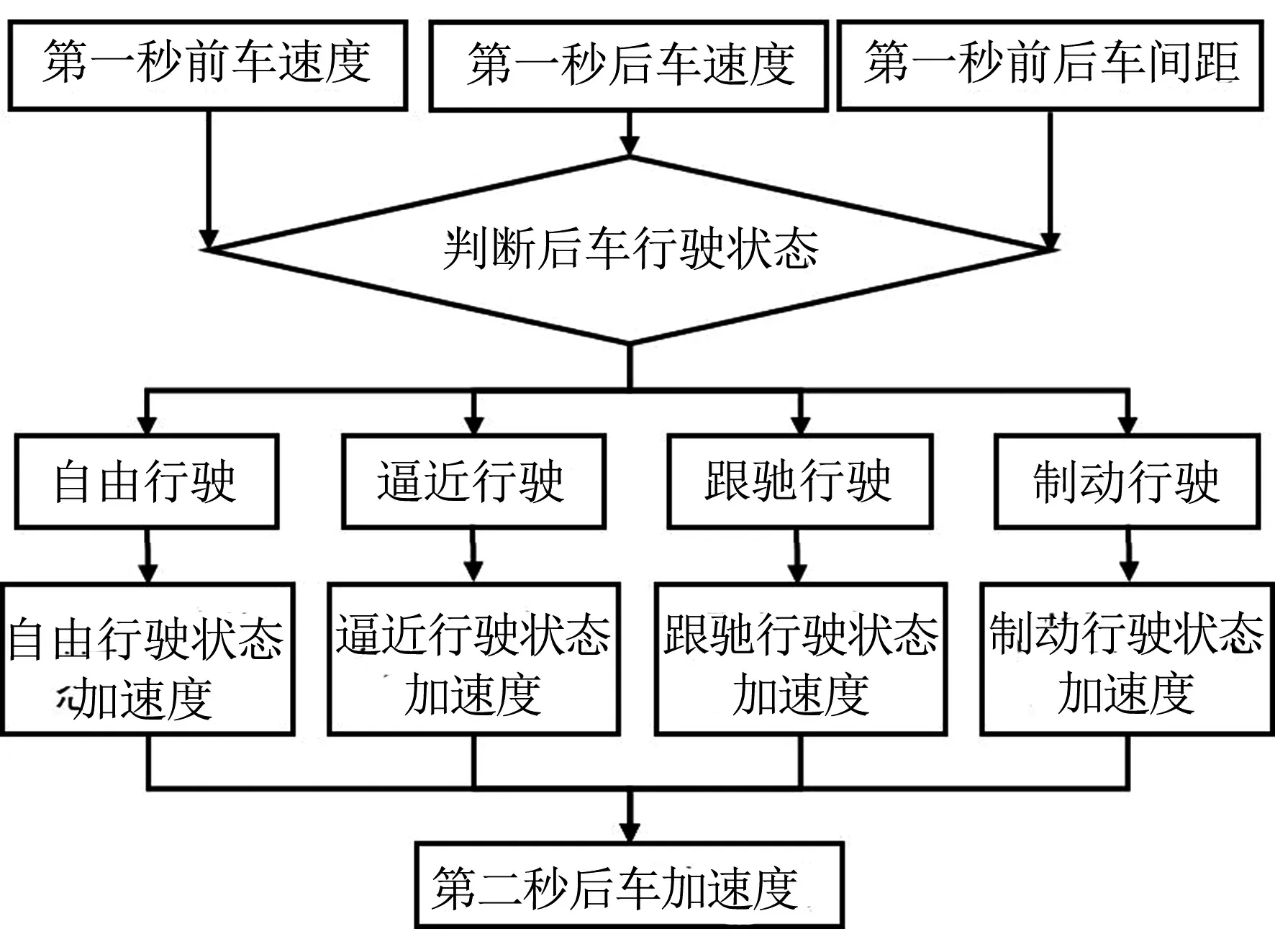
图3 跟驰后车加减速度计算思路

3 实测与仿真数据对比分析

3.1 速度分布对比分析

城市道路限速最高为60 km/h，本文通过划分速度区间计算平均行程速度来分析仿真和实测的速度整体分布情况.每个路段原始数据以60 s为间隔进行划分，求其平均行程速度，再将平均行程车速划分为30个速度区间，每个速度区间间隔单位为2 km/h，如[0 km/h，2 km/h]对应速度区间1，(2 km/h，4 km/h]对应速度区间2.分别将快速路、主干路、次干路和支路各个路段的实测后车速度数据和仿真后车速度数据进行对比分析，不同类型道路实测与仿真速度分布如图4所示.

由图4可以看出，在快速路路段实测速度区间峰值出现在速度区间25(48～50 km/h)，分布率为17%；仿真的峰值出现在速度区间24(46～48 km/h)，分布率为17%.仿真和实测的最大误差为10%，出现在速度区间24和25.仿真和实测的车辆速度偏高，主要由于快速路段不受信号灯影响，车辆不停车通过.在主干路段仿真和实测的峰值均出现在速度区间4(6～8 km/h)，分布率为14%.仿真和实测的最大误差为3.3%，出现在速度区间5.主干路段车速在速度区间1-5较为集中，主要是由于主干路交通流量大，信号灯控制等原因，导致车速在低速区间集中.在次干路段仿真和实测在速度区间12和13都呈现双峰值的情况，分布率为20%.仿真和实测最大误差为8.2%，出现在速度区间9.在支路仿真和实测的峰值都出现在速度区间8，实测峰值的分布率为18.5%，仿真峰值的分布率为22%.仿真和实测的最大误差为8%，出现在速度区间9.可见除了主干路段外，对快速路、次干路、支路的速度分布刻画存在一定误差.

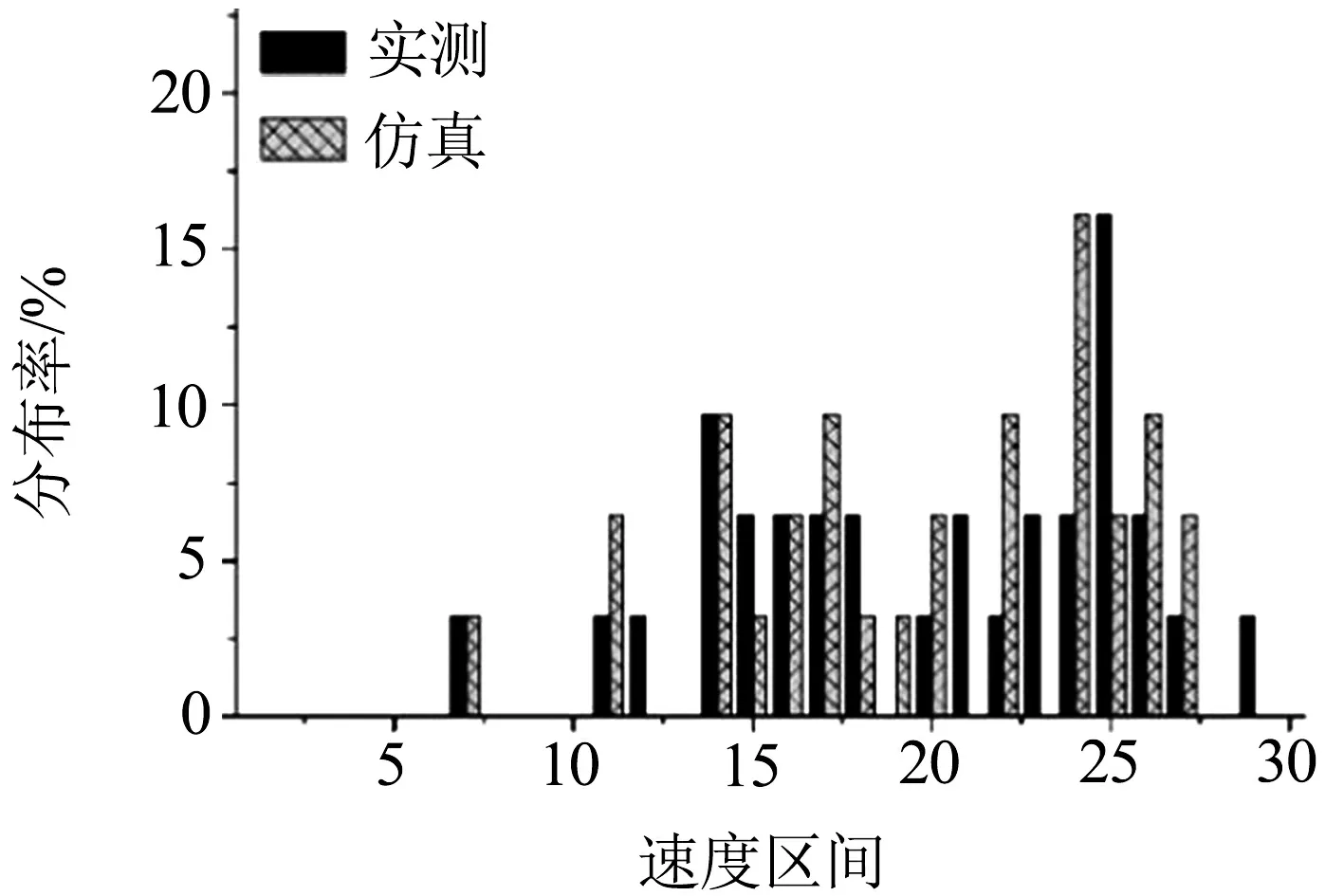
(a) 快速路仿真与实测速度区间分布

3.2 VSP对比分析

根据实测采集及仿真后得到的车辆逐秒加速度和速度数据，利用式(1)可以计算轻型车车辆的VSP.为了比较不同速度区间实测及仿真VSP分布情况，本文将收集到的车辆逐秒数据，根据速度划分为3个区间，低速区间[0～20 km/h)、中速区间[20～40 km/h)和高速区间[40～60 km/h)，不同区间的实测及仿真VSP分布情况如图5所示.

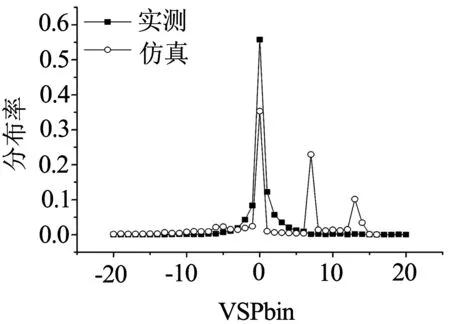
(a) 低速区间

从图5可以看出，由实测数据计算得出的比功率，在低速、中速、高速范围内，分布率峰值分别出现在VSPbin=0、VSPbin=1及VSPbin=2.进行正态分布检验后，发现实测数据的VSP在中速区间、高速区间均服从正态分布.同时，仿真得出VSP分布与实测数据相比存在较大差异.在峰值处，低速区间内，在VSPbin=0的区间，仿真与实测分布率相差了21.2%；中速区间内，在VSPbin=1区间，仿真和实测相差12.6%；高速区间内，在VSPbin=2区间则相差12.2%.由此可以看出Wiedemann74跟驰模型仿真得出数据在用于VSP计算时，存在较大误差.在中速和高速区间仿真得出VSP呈现不规律分布，因此不能将VISSIM仿真直接用于依托VSP的城市道路交通排放测算，需进一步对模型参数进行标定.

4 跟驰模型参数优化

4.1 遗传算法参数优化

本文选择遗传算法优化Wiedemann74跟驰模型参数， 寻找仿真及实测VSP均方误差最小的最优解，遗传算法模型中参数选择如表3所示，最终优化后参数值如表4所示.

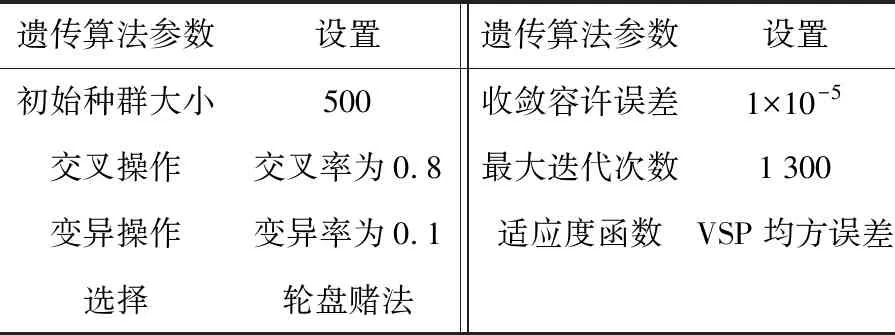
表3 遗传算法模型参数

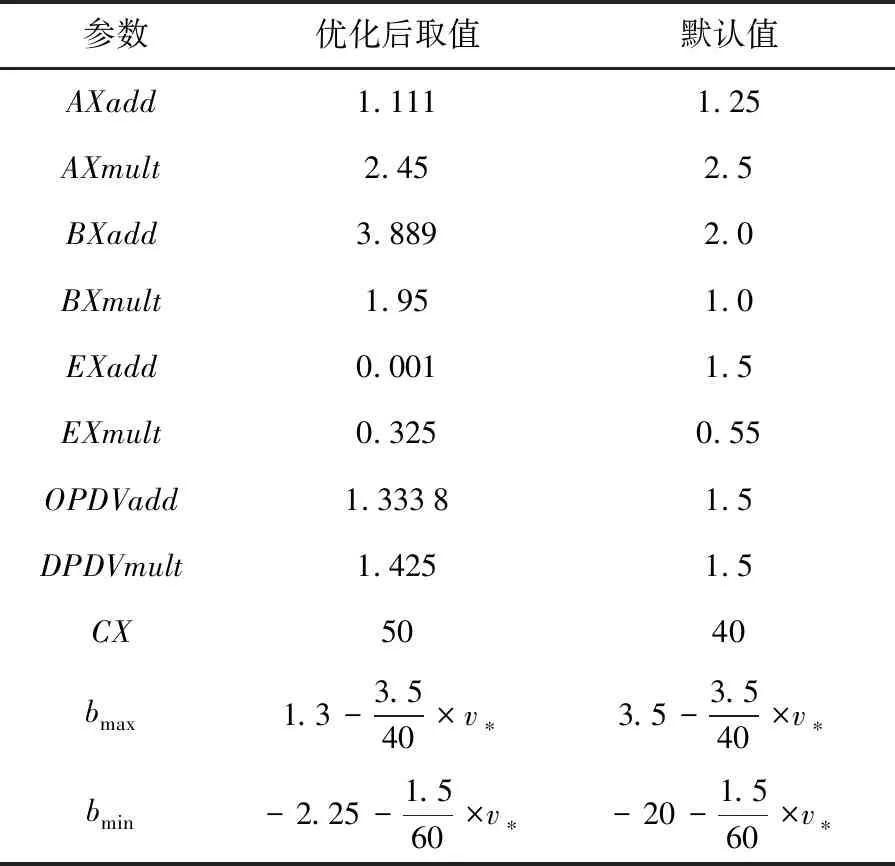
表4 遗传算法优化参数结果

4.2 优化效果分析

本文以跟驰模型参数为优化对象，寻找VSP均方误差最小的最优解.参数优化前后VSP均方误差分别为11.35及4.45，可见参数优化后，有效降低了仿真造成的VSP计算误差.优化后不同速度区间VSPbin分布如图6所示.由图6可以看出，在利用遗传算法对模型参数进行优化后，仿真计算得出比功率分布曲线与实测分布率曲线有相似的变化趋势.在中速和高速区间，仿真得出的VSPbin分布规律也服从正态分布.但是从图中可以看出，在最大迭代次数截止后，Wiedemann74跟驰模型对比功率分布刻画仍存在缺陷，仿真得出数据显示，仿真刻画的驾驶行为较实际情况更为激进.

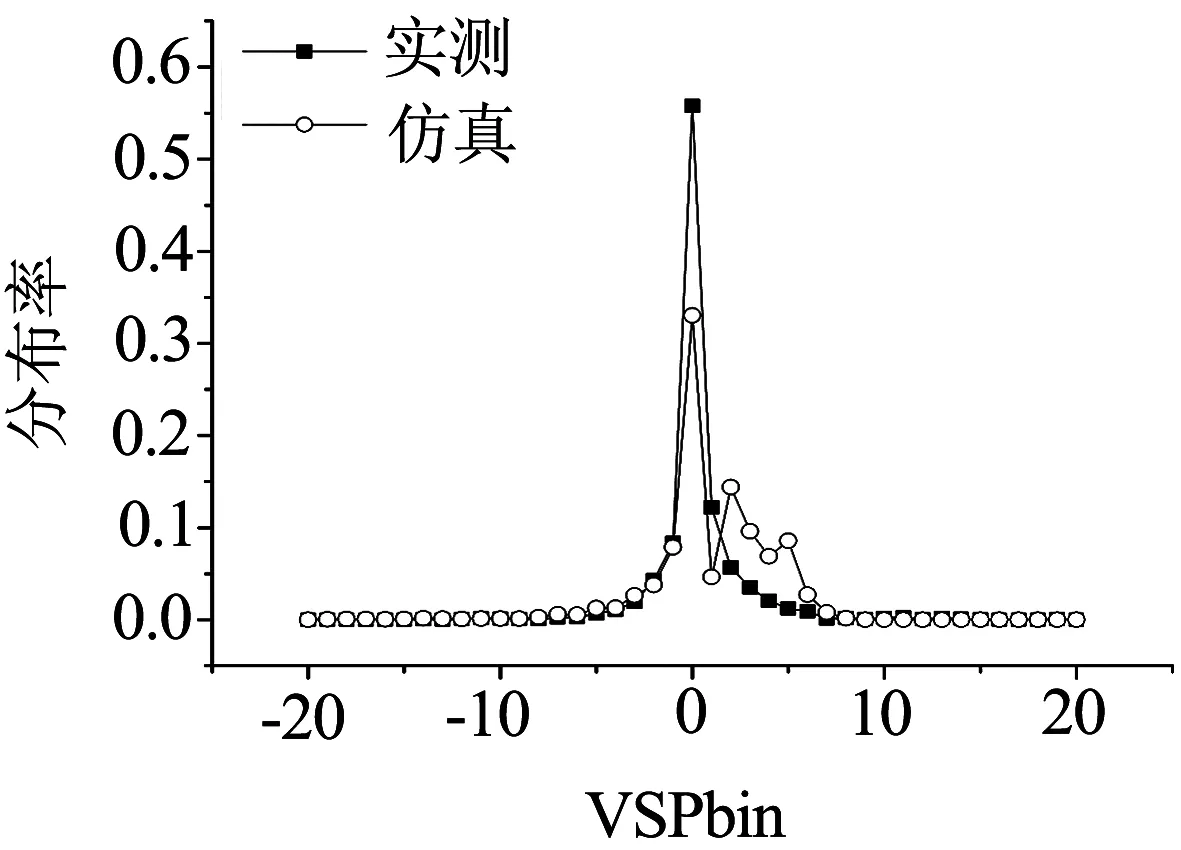
(a) 低速区间

为了进一步分析参数优化效果，对比仿真和实测排放估算误差，利用基于速度及比功率VSP的排放模型分别计算实测和仿真车辆平均排放因子.本文首先基于车载排放测试得到瞬时排放数据及工况数据，通过聚类分析得到基于速度及比功率VSP二维矩阵的汽油小汽车不同工况区间对应排放率表，如表5所示，排放计算结果如图7所示.

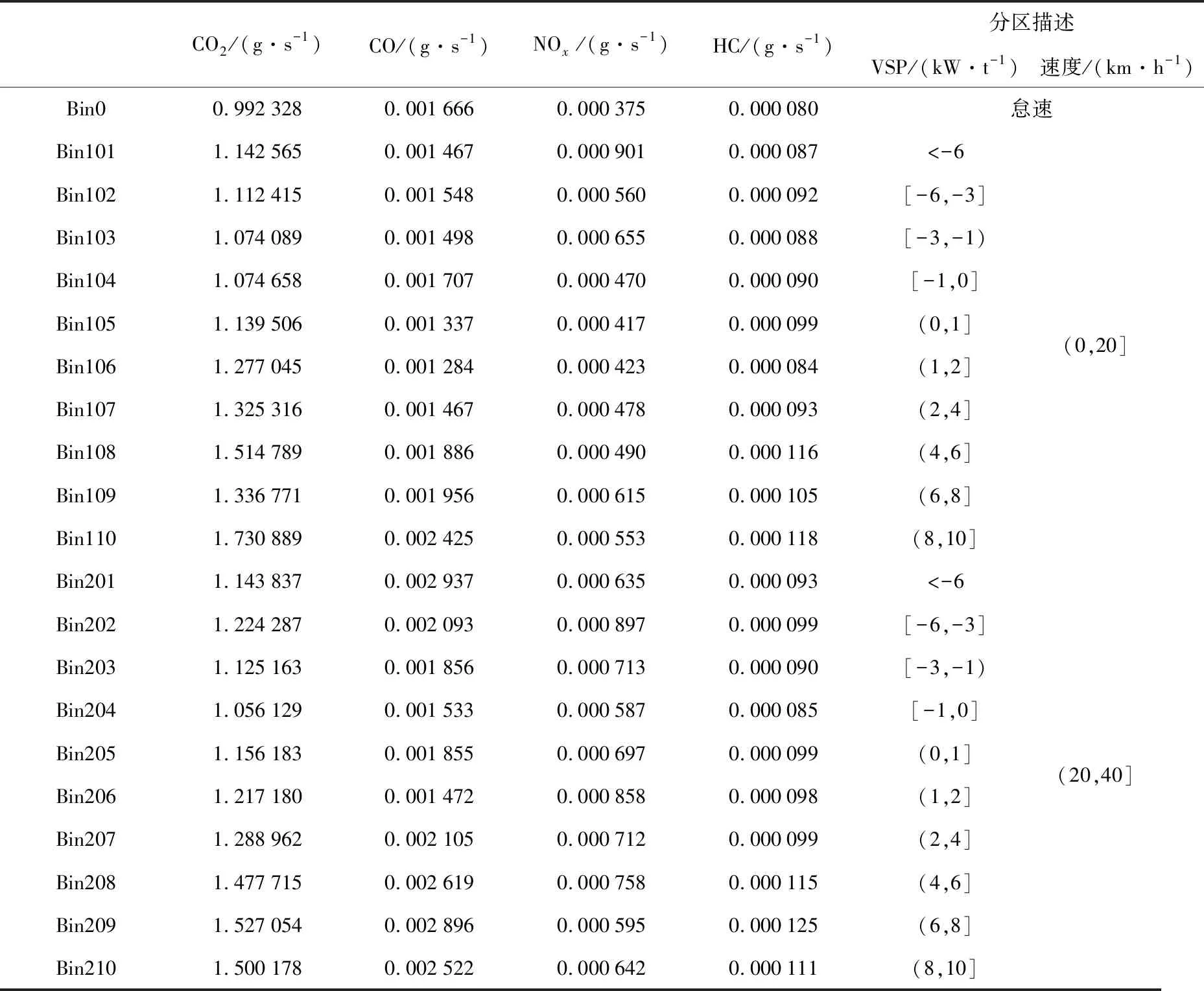
表5 汽油小汽车不同工况区间对应排放率表

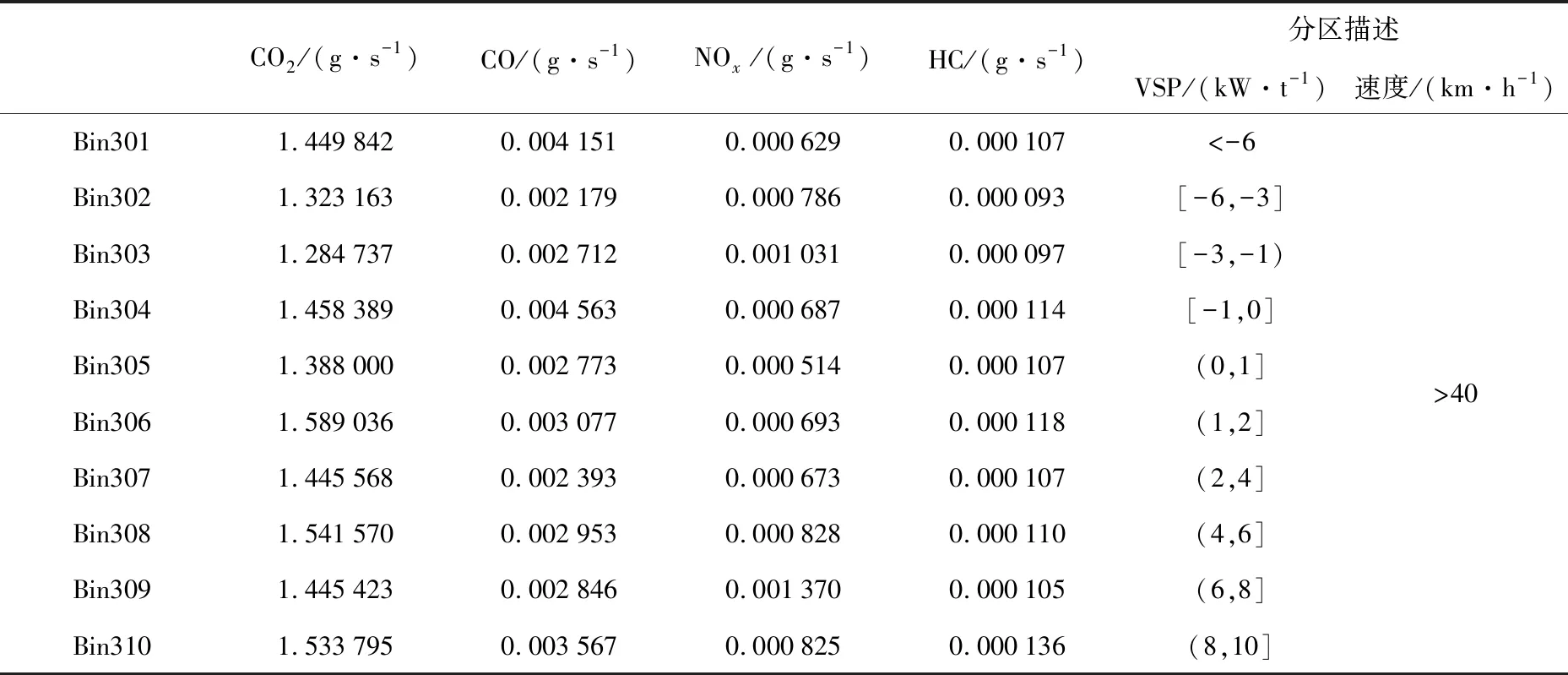
表5 汽油小汽车不同工况区间对应排放率表 (续表)

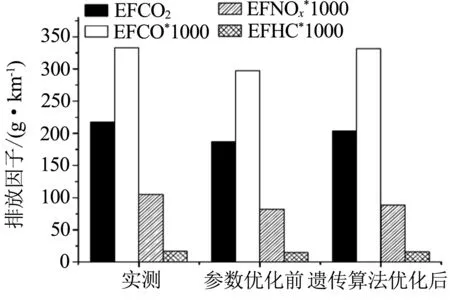
图7 实测和参数优化前后车辆排放因子

如图7所示，在不进行参数优化时，其仿真计算得出的CO2排放因子、CO排放因子、NOx排放因子和HC排放因子与实测相差13.75%、10.76%、21.54%和15.87%.而在利用遗传算法对跟驰模型参数进行优化后，排放计算误差明显减少，其中CO2、CO、NOx和HC排放因子与实测误差分别为6.33%、0.45%、15.16%、9.14%.

5 结论

比功率是排放测算的关键参数，本文运用跟驰数据采集设备，在西安市不同类型道路，实际测量前后车速度差、车头间距等数据.基于Wiedemann74跟驰模型机理，对比实测和仿真的平均速度分布及比功率分布，发现VISSIM对测试路段的平均速度分布刻画较为准确.但是VSP分布的仿真结果与实测存在较大差距，不能满足排放测算的需求.主要原因在于仿真模型对跟驰阈值刻画的不准确，而且仿真车辆加减速度分布较为分散，与实际驾驶行为不相符.之后采用遗传算法对模型参数进行优化，优化后仿真与实测的VSPbin均方误差及排放因子计算误差均有明显减少.