基于ICSA-MCKD方法的滚动轴承声信号微弱故障诊断
2022-10-08王树杰,李宏坤,王朝阁,孙斌,刘艾强
王 树 杰, 李 宏 坤, 王 朝 阁, 孙 斌, 刘 艾 强
(大连理工大学 机械工程学院,辽宁 大连 116024)
0 引 言
滚动轴承作为旋转机械的核心部件,通常承载着较大的荷载,当滚动轴承出现故障时,会造成机械传动故障,进而产生严重的经济损失.因此,对滚动轴承的诊断和监测可以提高机械系统的安全性和可靠性[1].目前,监测和诊断方法主要基于振动信号分析[2-4].然而振动传感器采用接触式方式安装,限制了其使用,而声音传感器采用非接触式,安装方便.声音信号包含丰富的信息,当机械设备发生故障时,声音信号会产生相应的变化.
针对声音信号低信噪比这一问题,提取出信号中的微弱故障信息是主要的研究方向,一些学者做了相关的研究.文献[5]以峭度为指标提出了最小熵反卷积(minimum entropy deconvolution,MED)算法,但是该算法对随机脉冲较为敏感,导致算法失效.为了充分利用轴承故障信号的周期性,文献[6]以相关峭度为指标提出了最大相关峭度反卷积(maximum correlation kurtosis deconvolution,MCKD)算法,克服了MED算法易受单个脉冲影响的问题.Miao等[7]对MCKD算法进行了改进,通过寻找包络信号的自相关最大值来估计迭代周期,克服了输入参数严格和复杂重采样的难题.申博文等[8]提出了基于最大相关峭度反卷积与自适应噪声完备集合经验模态分解的声信号故障特征提取方法,先用MCKD算法增强声信号中的冲击,然后再计算每个经验模态分量的峭度,选出最优分量,提取故障信息.Chen等[9]针对最大相关峭度反卷积、多点最优最小熵反卷积调整、最大二阶循环平稳盲反卷积等方法高度依赖测量信号先验周期的问题,引入了6种周期性检测技术来自适应地识别重复脉冲的周期.张俊等[10]将变分模态分解(variational mode decomposition,VMD)和MCKD相结合,并采用粒子群算法(particle swarm optimization,PSO)对VMD和MCKD中的参数组合进行寻优.刘尚坤等[11]将Teager能量算子和MCKD用于滚动轴承的故障识别,首先采用MCKD对信号进行降噪,然后使用Teager算子增强信号中的周期性冲击.Lyu等[12]用量子遗传算法(quantum genetic algorithm,QGA)自适应地选择MCKD的滤波器长度和反卷积周期,用于齿轮和轴承复合故障诊断.Wang等[13]提出了一种基于并行双参数优化共振稀疏信号分解(resonance-based sparse signal decomposition,RSSD)和优化的多点最优最小熵反卷积调整(multipoint optimal minimum entropy deconvolution adjusted,MOMEDA)的复合故障特征提取方法.
MCKD算法可以有效提取出滚动轴承声信号中的故障周期信息,然而其依赖于滤波器长度和先验故障周期的选择.布谷鸟搜索算法(cuckoo search algorithm,CSA)是一种生物启发式算法,该算法模拟了布谷鸟将自己的卵寄生在其他鸟类巢穴的行为.CSA具有优秀的全局寻优能力和局部寻优能力,但是该算法同其他生物启发式算法一样,也存在后期寻优精度低、迭代速度慢、易陷入局部最优的问题.Tsipianitis等[14]在算法中引入静态和动态惩罚函数,以增强CSA,并且结合鸟群算法(bird swarm algorithm,BSA)的关键参数,提出了具有动态惩罚的CS混合方法.Mareli等[15]提出了3种随迭代次数动态增加的发现概率函数,使全局寻优和局部寻优更加平衡,通过测试函数验证了该方法优于发现概率固定的布谷鸟搜索算法.李荣雨等[16]通过调整莱维飞行步长和在偏好随机游走中引入动态惯性权重及记忆策略,提高了算法的稳定性和搜索能力.针对CSA固定步长和发现概率问题,本文提出改进的布谷鸟搜索算法(improved cuckoo search algorithm,ICSA),在莱维飞行中引入步长尺度因子,在偏好随机游走中将固定发现概率调整为随迭代次数增加自适应调整的变发现概率.故本文将ICSA算法与MCKD算法相结合,用ICSA搜索出MCKD算法的滤波器长度和故障周期最佳组合,然后对反卷积后的信号进行包络谱分析,进行滚动轴承的故障诊断.
1 基本原理
1.1 最大相关峭度反卷积
实测信号xn(n=1,2,…,N)是源振动信号sn(n=1,2,…,N)与传递路径h卷积得到的,MCKD是通过寻找一个FIR滤波器,进行反卷积运算得到源信号sn的近似解yn(n=1,2,…,N):
(1)
式中:f(f1,f2,…,fL)为滤波器,L为滤波器长度,*为卷积运算.
通过最大化相关峭度求解滤波器f,相关峭度的定义为
(2)
式中:T为故障周期,T=fs/fi,fs为采样频率,fi为故障特征频率;M为位移数,一般取M=7.
最大化相关峭度求解滤波器f(f1,f2,…,fL):
(3)
相关峭度对滤波器求导:
(4)
由式(1)~(4)可求得滤波器的系数,并表示成矩阵形式:
(5)
式中
综上所述,MCKD算法的流程如下:
(1)初始化故障周期T、滤波器长度L、位移数M等参数;
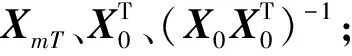
(4)根据yn计算αm、β;
(5)更新滤波器f;
(6)判断ΔKc,M(T)是否小于阈值,若小于阈值,结束迭代,否则重复步骤(3)~(5).
1.2 CSA
CSA由控制全局搜索的莱维飞行和局部搜索的偏好随机游走组成.在CSA中有3条理想化规则:
(1)每只布谷鸟一次产一个卵,并随机选择一个寄生鸟巢.
(2)最高质量的卵可以存活到下一代.
(3)寄生鸟巢数量固定,且寄生卵被发现的概率是pa.当宿主发现寄生卵后,会选择抛出寄生卵或者放弃鸟巢重新筑巢.
每个寄生鸟巢代表一组解,通过莱维飞行更新鸟巢位置:
(6)
(7)
式中:μ和ν服从标准正态分布,β=1.5.
(8)
莱维飞行的步长
(9)
式中:α0为步长因子,通常α0=0.01;Xb表示当前最优解.
综合式(6)~(8)通过莱维飞行到达的新位置为
(10)
在莱维飞行后,产生一个随机数与发现概率pa比较,一般取pa=0.25,当随机数大于pa,代表寄生卵被发现,进行偏好随机游走,产生新的鸟巢:
(11)
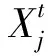
1.3 ICSA
在标准CSA中,莱维飞行的步长因子α0是固定的,但是步长因子对给定的优化问题会很敏感,若α0一直较大,则算法的全局搜索能力很强,但是会降低搜索精度,若α0一直较小,会导致算法收敛太慢.α0可以是固定的或是变化的[17],故本文引入步长尺度因子,提出变步长的CSA(ICSA),将式(9)改为式(12):
(12)
式中:F为步长尺度因子,服从[0,1]上的均匀分布.
式(10)更新为式(13):
(13)
在标准CSA中,偏好随机游走的发现概率pa为固定值0.25,pa是局部最优解搜索的关键,pa太大会导致搜索精度不够,pa太小会导致错过最优解,使得算法收敛过慢.故本文提出了随迭代次数更新的发现概率,在算法开始时,pa较小,增加算法的搜索精度,在算法后期,有较大的pa,增加算法的收敛速度.调整固定pa为式(14):
(14)
1.4 ICSA-MCKD方法
在用ICSA优化参数时,需要确定一个适应度函数.文献[18]提出了谐波显著性指标(harmonic significant index,HSI)来识别故障信息,其表达式为
(15)
式中:F(ω)为故障频率ω处的幅值,K为要计算的谐波数量,N(ω)为ω附近的噪声量,P(kω)=F(kω)/N(kω)表示故障频率ω的显著程度.但是,该指标对于实际信号不能完全适用:
(1)计算ω附近的噪声量N(ω)时,均采用ω左右各5个频率点对应的幅值进行平均,没有考虑内圈故障时转频的调制影响,不能反映出故障频率周围的整体噪声.
(2)H(ω)为多阶谐波指标相乘,受单阶谐波指标影响较大,当只有某一阶的谐波指标较大,而其他阶谐波指标较小时,也会使H(ω)值较大,导致误判.
基于以上问题,提出调整的谐波显著性指标(adjusted harmonic significant index,Ha),将其作为ICSA-MCKD的适应度函数,其表达式为
(16)
式中:F(kω)为反卷积信号的包络谱在kω处的幅值,N(kω)为kω左右转频范围内的平均噪声,a(·)为取均值.调整的谐波显著性指标计算kω附近以转频为间隔的边频带内的噪声量而不是左右各5个频点,考虑了转频的调制作用;计算多阶谐波指标的平均值,克服了只有单阶谐波指标较大导致HSI误判的问题.
综上所述,ICSA-MCKD故障诊断方法的流程如图1所示,主要步骤如下:
(2)计算每个鸟巢的目标值,找到当前位置目标值最大的鸟巢,作为最优鸟巢Xb.
(3)进行莱维飞行,更新位置,最优鸟巢保持不动.计算新位置下每个鸟巢的目标值Ha(ni),并与旧鸟巢的目标值比较,如果新鸟巢目标值大于旧鸟巢目标值,则替换旧鸟巢.
(4)进行偏好随机游走,计算新鸟巢的目标值,如果大于旧鸟巢的目标值,则替换旧鸟巢.
(5)选择最优解,判断是否满足迭代停止条件,若满足,则根据最优参数组合进行MCKD滤波,进而进行包络谱分析,若不满足则返回步骤(3)继续循环.
2 仿真研究
为验证本文提出的方法对滚动轴承故障诊断的有效性,构造了内圈故障轴承的仿真信号:
x(t)=e(t)+r(t)+p(t)+n(t)
其中
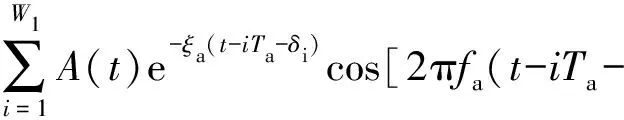
δi)+φa]
徐进步一拍脑袋:“啊,想起来了,‘世上本无路’那一句,难怪听着有印象。可就他,八成没读过鲁迅的什么书吧?”
式中:e(t)代表故障脉冲信号,W1=128为故障脉冲个数,A(t)=0.5(1-cos(2πfrt))为故障脉冲幅值,fr=10 Hz为转频,Ta=1/128 s为脉冲间隔时间,即故障特征频率为fi=128 Hz,fa=2 600 Hz为固有频率,ξa、δi、φa分别为衰减系数、滚子滑移时间延迟和初始相位.r(t)为随机脉冲信号,W2=3为脉冲个数,振幅Bs和出现时间Ts分别服从正态分布和均匀分布,fb=1 700 Hz.p(t)代表谐波信号,W3=2为谐波个数,且谐波频率f1=10 Hz,f2=20 Hz.n(t)为高斯白噪声.加入噪声后信噪比为-11.6 dB,采样频率为12 800 Hz,采样时间为1 s.
图2(a)为各分量及加噪后的仿真信号时域图,故障周期信号已经被噪声淹没;图2(b)为仿真信号包络谱,由于噪声干扰,图中难以看出故障特征频率.
现将本文的方法用于仿真信号处理.利用ICSA优化MCKD参数组合,初始化ICSA的参数,鸟巢个数n=15,最大迭代次数tmax=50,目标函数为Ha(ni).滤波器长度L的搜索区间为[100,1 000],故障周期T的搜索区间为[98,102].
为验证ICSA的优越性,用CSA和PSO对同一仿真信号进行参数寻优,图3(a)为各参数优化算法的迭代图,为了公平起见,CSA的初始化参数和ICSA的保持一致.PSO的种群个数和最大迭代次数也与ICSA的保持一致,分别为n=15,tmax=50,学习因子c1=c2=1,惯性权重w=1.滤波器长度L和故障周期T的搜索区间都分别设置为[100,1 000]和[98,102].从图中可以看出,ICSA在迭代30次时达到最优解,Ha为3.434;CSA在迭代37次时达到最优解,Ha为3.205;PSO在迭代33次时达到最优解,Ha为2.832.Ha作为反卷积效果的一个标准,Ha越大,说明反卷积效果越好,故障特征越明显.由此可见,ICSA在迭代次数最少时有最大的适应度函数值,故ICSA有更快的迭代速度和搜索精度.ICSA的寻优参数组合为L=217,T=100,该参数下MCKD反卷积信号的包络谱如图3(b)所示,在图中可以明显看到故障特征频率128 Hz及其倍频,并且可以看到转频调制的边频带,证明了本文方法的有效性.
为了证明ICSA对MCKD参数寻优结果的可靠性,现改变最佳参数组合中的一个,并以更改后的参数组合输入MCKD中对仿真信号进行处理.图4(a)为将最佳参数组合[217,100]中的滤波器长度L改为215后的MCKD反卷积信号包络谱.与图3(b)相比图4(a)中内圈故障特征频率的四倍频、五倍频被噪声干扰严重,看不出明显的边频带,且内圈故障特征频率及其倍频的幅值都有所下降.图4(b)为将最佳参数组合[217,100]中的故障周期T改为101后MCKD反卷积信号的包络谱.与图3(b)相比图4(b)中只能隐约看出内圈故障特征频率及其二倍频和三倍频,且噪声干扰严重,而高阶倍频都被噪声淹没.通过图4(a)与图4(b)的对比分析可知,MCKD对参数的选择有很大的依赖性,且对故障周期T的选择更为敏感.而人为主观地选择参数具有偶然性,导致反卷积效果不理想,而通过ICSA自适应地选择参数,可以达到最佳的分析效果.
为了凸显MCKD的优越性,采用MED对上文的模拟信号进行处理,MED的滤波器长度和MCKD的一致(L=217),经MED滤波处理后信号的包络谱如图5所示,没有明显的故障特征频率及其倍频,说明MED对有随机冲击和强噪声信号没有很好的作用,对比图3(b)和图5可知,MCKD有更好的故障信息提取能力.
3 试验研究
为了进一步验证该方法的有效性,现对滚动轴承内圈故障的实测信号进行分析.试验在QPZZ-Ⅱ试验平台上进行,如图6(a)所示.测点1选在远离轴承座的位置,测点方向为正对轴承座,以模拟声音信号的微弱故障,另选测点2靠近轴承座的位置做对比,测点方向也为正对轴承座,如图6(b)所示.轴承内圈故障如图6(c)所示,加工方式为线切割,所用轴承型号为NU205EM/PS,具体参数如表1所示.使用PCB噪声麦克风和NI9234采集卡采集声音信号,设置采样频率为12 800 Hz,采样时间为2 s,转速为900 r/min,根据理论公式计算fi=116.25 Hz,T=110.
现分别对测点1和测点2处信号进行包络谱分析,图7(a)为测点2处信号的包络谱,在图中可以明显看到内圈故障特征频率及其二倍、三倍故障特征频率,以及转频调制的边频带.虽然,通过测点2处信号的包络谱可以判断出故障特征,但是故障特征频率被转频及其倍频以及噪声所干扰,对故障诊断造成困难.图7(b)为测点1处信号包络谱,在图中只能看到明显的转频以及二倍转频,而故障频率被噪声淹没,无法判断故障信息.由此可得出结论:声音信号对距离较为敏感,考虑到实际工程应用中,传感器距被测对象都有一定的距离,故需要对实测信号进行进一步的处理.
现用本文提出的方法对测点1处的信号进行处理.初始化ICSA的参数,鸟巢个数n=15,最大迭代次数tmax=50,目标函数为Ha(ni).滤波器长度L的搜索区间为[100,1 000],故障周期的搜索区间为[108,113].
为验证ICSA对实际信号也有很好的搜索性能,与CSA、PSO对同一试验信号进行参数寻优.图8为各参数优化算法的迭代图,CSA和PSO的初始化参数同仿真信号保持一致,滤波器长度L和故障周期T的搜索区间都分别为[100,1 000]和[108,113].从图中可以看出,ICSA在迭代33次时达到最优解,Ha为6.596;CSA在迭代39次时达到最优解,Ha为6.482;PSO在迭代47次时达到最优解,Ha为6.41.由此可见,ICSA在迭代次数最少时有最大的适应度函数值,故ICSA 有更高的迭代速度和搜索精度.
ICSA的最佳寻优参数为L=622,T=111.5,该参数下MCKD反卷积信号的包络谱如图9(a)所示,在图中可以明显看到故障特征频率115.5 Hz及其倍频.CSA的最佳寻优参数为L=654,T=111,该参数下MCKD反卷积信号的包络谱如图9(b)所示,相比于图9(a),整体谱线幅值更小,噪声干扰更大,证明了ICSA的寻优优越性.
为验证故障周期的选择会影响MCKD对实际信号的反卷积效果,现把最佳参数组合[622,111.5]中的故障周期换为理论故障周期110,进行MCKD反卷积,图10为反卷积后的包络谱.与图9(a)相比图10中故障频率的高阶倍频被噪声干扰严重,且整体谱线的幅值都有所下降.说明在实际工程问题中,转速波动以及滚动体滑移会导致实际故障特征频率与理论计算值有一定的误差,用理论值作为MCKD的先验参数会导致故障特征不明显,对故障诊断造成困难.
为了凸显MCKD对实际信号处理的优越性,对同一实际信号用MED进行滤波处理,MED的滤波器长度和ICSA-MCKD的一致(L=622),对MED滤波后的信号进行包络谱分析,如图11所示,图中虽能找到故障特征频率,但是噪声干扰严重,对比图9(a)和图11可知,MCKD有更好的故障特征提取能力.
4 结 语
本文提出了一种基于改进的布谷鸟搜索算法(ICSA)和最大相关峭度反卷积(MCKD)相结合的滚动轴承故障诊断方法,通过仿真信号和实际信号的比较,证明了该方法的有效性和优越性.MCKD可以在强噪声背景下提取出滚动轴承的故障信息,然而从实测信号分析可知,由于转速波动和滚动体滑移等因素的影响,滚动轴承的实际故障频率和理论计算值存在偏差,这就会影响MCKD的效果,故本文提出使用参数优化算法搜索MCKD的最佳参数组合.CSA在算法后期存在寻优精度不足和收敛速度较慢的问题,本文提出了ICSA,在莱维飞行中引入了步长尺度因子和自适应发现概率,提高了算法的搜索精度和迭代速度,并与CSA、PSO算法对比,验证了ICSA的优越性.
