考虑随机维修质量的退化系统选择性维修策略
2022-10-08曹慧,段富海
曹 慧, 段 富 海
(大连理工大学 机械工程学院, 辽宁 大连 116024)
0 引 言
复杂退化系统的特点是系统组成部件数目较多,各部件间存在着明显的结构特征,如串/并联、冗余、k-n、桥等.受环境、负载、老化等问题影响,系统部件的性能特征逐渐退化直至失效.系统常配备连续监测部件,如传感器、计量仪表等,能够实时获取系统部件退化状态数据信息.当复杂系统执行到某退化状态需进行维修操作,但由于维修资源有限,如维修时间和成本有限,不能同时对所有系统部件进行适当维修操作时,可采用选择性维修策略[1].
复杂退化系统的选择性维修方式主要有更换性维修和预防性维修两种.更换性维修使系统“修复如新”,是完美的维修方式.而预防性维修可将系统恢复到介于“修复如新”和“如旧”的中间状态,是一种非完美的维修方式.在实际工程应用中,这两种维修方式可以描述大部分的维修活动.Nakagawa[2]率先在风险率或役龄模型中引入改善因子来描述预防性维修的非完美属性,提出了一种结合风险率模型和役龄退回模型优点的混合模型.Pandey等[3]和Liu等[4]基于混合模型,讨论了考虑预防性维修的复杂系统选择维修问题.在上述研究中,预防性维修的改善因子通常假定为常数.实际上,由于维修人员的专业水平、工具和维修环境等因素的限制,系统维修质量往往是随机的.针对这一问题,Duan等[5]提出一种基于随机维修质量的系统选择性维修模型.然而,该模型忽略了系统部件以往维修情况对维修质量的影响.在退化系统的维修决策中,系统部件的维修情况会影响其退化状态,而系统部件的退化状态直接影响了系统维修质量.因此,在建立适用于退化系统的随机维修质量模型时,还应充分考虑系统部件以往的维修情况.
综上所述,本文以退化状态可监测的复杂系统为研究对象,提出基于部件随机维修质量的选择性维修策略.该策略以系统执行下一任务的预测可靠度为目标建立维修优化模型并利用遗传算法(GA)搜索得到系统最优维修决策,从而为决策者制订合理的系统维修计划提供理论支撑.
1 退化系统可靠度模型
1.1 系统部件可靠度模型
本文选择Wiener过程作为刻画部件性能退化过程的基础模型.令随机过程X(t)(t≥0)表示部件i的性能退化量.部件i的退化过程可用如下线性Wiener过程刻画:
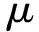
(1)
假设部件退化量Xi(t)累积到设定失效阈值li时发生退化失效,可定义部件失效时间Ti为退化量Xi(t)首次到达或超过失效阈值li的时间,即
Ti=inf{t|Xi(t)≥li,t≥0}
(2)
易知Ti应服从逆高斯分布.
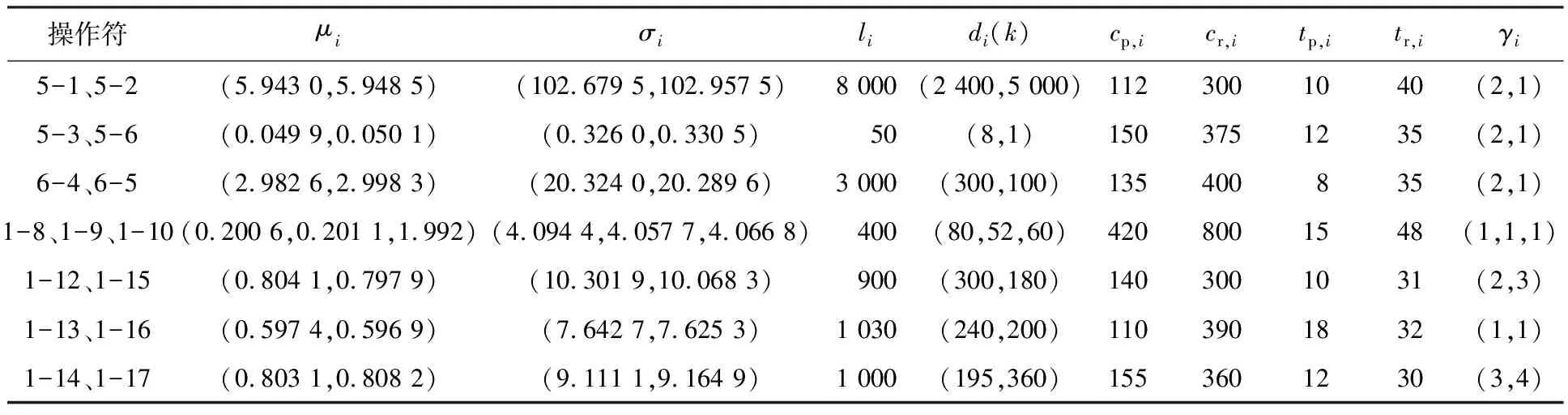
假设部件i运行到时刻τ仍未失效,且当前性能退化量为dτ,i(dτ,i Tτ,i=inf{t|Xi(t+τ)≥li,Xi(τ)=dτ,i,t≥0}= inf{t|Xi(t+τ)-Xi(τ)≥li-dτ,i,t≥0}= inf{t|Xi(t)≥li-dτ,i,t≥0} (3) 失效时间Tτ,i仍服从逆高斯分布,其密度函数只需将Ti密度函数中的失效阈值li替换为li-dτ,i即可. 由可靠度的定义可知,可靠度是在规定时间内系统及部件能够正常运转或服务正常的概率.因此,部件i的可靠度可表示为Ri(t)=1-Fi(t).即可得到部件i运行到任意时刻τ时,关于时间t的预测可靠度,可表示为 (4) 鉴于复杂退化系统的特点是系统部件数目较多,且各部件间存在着明显的性能退化特征,本文采用GO法[6](goal oriented methodology)建立系统退化可靠性评估模型.GO法系统可靠性分析的过程是以操作符描述系统各部件,再以信号流连接操作符建立的系统GO图模型.对系统GO图进行GO运算,得到系统输出状态值和状态概率,再评估系统可靠性[7-8]. 根据退化系统的特点,需对系统选择性维修过程做如下基本假设: (1)系统由n(i=1,…,n)个部件组成,在系统运行过程的任意时刻,描述部件性能退化状态的累积退化量可通过传感器监测得到. (2)系统进入维修间隔期后,系统部件的退化进程进入停滞状态.维修人员可根据系统部件当前的退化水平和故障状态,对各部件执行预防性更换或维修操作.各维修操作均可有效改善部件当前的退化水平,改善程度与部件当前退化水平有关. (3)经更换性维修后,系统部件状态恢复到完好状态.经预防性维修后,系统部件恢复到介于完好状态和当前退化状态的中间状态. (4)系统采取的任何维修操作都在维修间隔期内完成,执行维修操作所需维修人员、备件充足,且维修过程不受维修地点和维修工具等的限制. 一般地,维修后系统部件的状态取决于采取何种维修操作方式,且各种维修方式的维修质量应与分配给该部件的维修费用和部件当前的退化状态有关[5]. (5) (6) 式中:a、b是维修费用的调整参数;ci表示部件i的维修费用,cr,i表示部件i的更换性维修费用,0 若系统部件已经经历了多次预防性维修操作,部件i的预防性维修质量随预防性维修次数的增多而下降.此时,系统部件的维修质量还应与该部件已执行维修操作的次数有关. (7) 式中:g是模型的调整参数.γi表示部件i的维修次数,γi=1时,表示进入当前维修间隔期前,部件i未进行预防性维修操作,且在当前维修间隔期内部件首次采取预防性维修操作时,式(7)与式(6)形式相同. (8) (9) 式中:g1、g2是模型的调整参数. (10) 累积分布函数可表示为 (11) 综上所述,在预防性维修质量随机的条件下,若已知系统执行第k+1次任务的时间为θk+1,则对于执行第k次任务后退化量已知的任意系统部件i,根据式(4)可得该部件维修后,执行第k+1次任务的预测可靠度: (12) 假设在系统第k次任务完成后的维修间隔期内,若系统部件i被选择执行维修操作,则其要么更换,要么进行预防性维修.且考虑到系统多个部件同时进行维修时,存在正的经济相关性[9-10],维修总费用应减去由共同维修多个部件节省的基本维修费用.此时,系统总维修费用表示为 (13) 式中:cs表示系统执行维修操作的基本费用;C(k)表示系统第k次任务完成后的维修间隔期内,系统维修操作消耗的总费用;cp,i表示部件i的预防性维修费用,cr,i表示部件i的更换性维修费用,0 同理,系统总的维修时间应为所有选择维修操作部件消耗的维修时间之和,表达式为 (14) 式中:T(k)表示系统第k次任务完成后的维修间隔期内,执行维修操作消耗的总时间;tp,i表示部件i的预防性维修时间,tr,i表示部件的更换性维修时间,0 在完成第k次任务进入维修间隔期后,系统选择性维修策略优化过程为以系统执行第k+1次任务的总维修费用和总维修时间为约束,以最大化系统执行第k+1次任务的预测可靠度为目标进行优化,从全部系统部件中选择亟待维修部件并确定其维修操作方式.选择性维修优化目标模型可表示为 (15) 式(15)限制了系统总的维修费用不能超过设定维修成本c0及系统总的维修时间不能超过设定维修时间t0. 本节采用遗传算法(GA)解决退化系统选择性维修目标优化问题[11].基于GA的维修优化过程:首先,随机生成包含所有系统部件维修决策信息的二进制编码向量作为初始种群.该维修决策向量的编码方式如图1所示.根据系统部件的维修选择情况和维修方式,每个部件可分配2 bit空间,1 bit表示维修选择变量Vi(k),1 bit表示部件的维修方式变量εi(k).以图1所示的n部件编码结构为例,部件1编码为01,说明其未被选择进行维修;部件2编码为11,说明其被选择且进行了预防性维修操作.根据系统部件的数量,种群中维修决策向量个体长度应为2n,算法的搜索空间应为22n. 其次,计算种群中各向量的适应度,从种群中选择满足最优适应度的向量作为亲本进行交叉和变异操作.当迭代次数达到设定值时,确定在相应维修约束条件下,优化目标模型达到最优值的维修决策向量. 表1 系统部件退化状态与维修资源参数 GA的优化过程参数设置如下:种群大小设置为200,最大迭代次数g=300,交叉、变异概率设置为0.2.GA的迭代过程收敛性如图3所示.算法优化得到的系统最优维修决策如表2所示. 由表2可知,考虑预防性维修时,系统维修的最优决策为操作符5-1、5-2、1-12和1-17采取更换性维修操作,操作符5-3、1-14和1-15采取预防性维修操作,其余部件则未被选择采取维修操作.此时,根据随机维修质量模型得到的系统执行第k+1次任务的预测可靠度为0.839 5,系统维修所需的费用为1 693美元,维修时间为175 h. 表2中还给出了在确定维修质量模型(考虑、不考虑维修次数两种情况),以及不考虑维修次数时的随机维修质量模型等各种维修质量模型下,系统的预测可靠度评估结果.通过比较可知,(1)考虑随机维修质量下,系统预测可靠度为0.846 2、0.839 5,分别高于同类确定质量模型得到的系统预测可靠度0.01%、4.48%;(2)考虑维修次数的维修质量模型得到的系统预测可靠度为0.794 7、0.839 5,相较同类模型不考虑维修次数时分别降低了5.14%、0.67%. 进一步分析给定的维修资源总量大小对系统维修优化结果的影响,以执行第k+1次任务的系统最大化预测可靠度为优化目标时,最大预测可靠度相对维修费用和维修时间敏感性如图4所示.其中,将系统维修时间设定为175 h,令系统维修费用在[1 300,1 900]美元内以步长100美元逐渐增加,得到的系统最大预测可靠度在图4(a)中给出.将系统维修费用设定为1 700美元,令系统的维修时间在[135,195]h内以步长10 h逐渐增加,得到的系统最大预测可靠度变化情况在图4(b)中给出. 根据图4可知,系统执行第k+1次任务的最大预测可靠度随给定的维修费用和维修时间的增加而增大.图4(a)中,系统预测可靠度的增大趋势停止在1 600美元,随后因受限于维修时间,随着维修费用的增加,系统的预测可靠度不再增大.类似地,在图4(b)中,受限于维修费用,系统预测可靠度随维修时间的增长趋势停止在185 h. 本文建立了以可靠度为中心的选择性维修策略模型,并在所建立的维修决策模型中,充分考虑了系统非完美维修部件的随机维修质量对系统可靠性评估和维修决策的影响.根据航空发动机控制系统算例的仿真结果可知:(1)受维修次数的影响,部件随机维修质量水平降低,系统可靠度评估结果为0.839 5,相较于确定维修质量的评估结果降低0.66%.(2)系统执行下一任务的预测可靠度随着维修资源水平的增加而增长.在某一维修资源为定值时,系统预测可靠度的增长幅度最终将因受限于该资源而趋于稳定.可见,利用本文所提系统部件随机维修质量模型进行系统可靠性评估,所得结果准确有效,可用于指导后续系统维修决策.同时,基于随机维修质量的选择性维修策略还可帮助维修决策者在制订合理维修计划的同时避免维修资源的浪费.1.2 系统可靠度分析模型
2 退化系统选择性维修策略
2.1 系统维修过程基本假设
2.2 系统部件维修质量模型
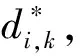
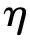
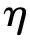
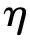
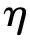
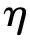
2.3 维修费用和时间模型
2.4 维修优化模型
3 算例分析
4 结 语
