岩石三维裂纹扩展问题的近场动力学数值模拟

2022-10-08李春光

同济大学学报（自然科学版） 2022年9期

崔昊，郑宏，李春光，韩月

（1. 中国电建集团华东勘测设计研究院有限公司，浙江杭州 311122；2. 北京工业大学城市建设学部，北京 100124；3. 中国科学院武汉岩土力学研究所，湖北武汉 430071）

外部荷载作用下岩体内裂纹的扩展与贯通往往导致岩石工程发生失稳破坏，因此预测岩体中裂纹的扩展过程对于揭示岩体的变形和破坏规律以及评价岩土工程的安全性具有重要意义。目前，受困于研究手段的不足，对岩体裂纹扩展规律的研究仍集中于二维空间内。但实际工程中的岩体裂隙，无论深埋于岩体内部或只露于浅层表面，其本质都是三维裂纹扩展问题，因此，对岩体三维裂隙扩展的研究更具有实际意义［1］。

预测三维裂纹的扩展是一项极具难度的问题。在理论研究方面，由于三维裂纹扩展问题的复杂性、多样性与求解上的巨大难度，至今仍未有理论上的相关突破。在室内试验方面，一般采用类岩石材料或CT 扫描方式对三维裂隙岩体的破裂机理进行研究［2］，但由于岩体内部裂纹扩展观测手段的匮乏，室内试验尚无法满足工程问题的需要。

由于理论分析与室内试验的缺乏，学术界对三维裂纹扩展的研究集中于数值方法。有限元法（FEM）是最早用于模拟裂纹扩展问题的数值方法，但FEM在模拟裂纹扩展时需要不断地重新划分网格，极大地增加了计算工作量。对于复杂的三维裂纹问题，网格的切割划分更具挑战性。鉴于FEM的这些缺陷，出现了基于点近似的无网格方法［3］。该方法不需要随裂纹扩展进行网格重构工作，降低了裂纹扩展问题的难度。但无网格方法中也引入了一些新的缺陷［4］，如：①本质边界条件的施加相对复杂；②计算量更大；③配点型无网格计算稳定性差等。

鉴于传统数值求解方法在处理裂纹扩展问题时的不足，Silling［5］提出了基于非局部作用思想的近场动力学（Peridynamic，PD）方法。该方法以非局部作用的积分模型代替传统理论的微分模型，避免了因在位移不连续处求导引起的奇异性问题。2007 年Silling 等［6］提出了更为广泛的非常规态基PD（Nonordinary state-based peridynamic，NOSB-PD）理论，该理论借助变形梯度张量F在PD 框架下引入经典力学中的应力与应变，搭建了微观键与宏观强度准则间的关系，因而在岩土工程领域得到了广泛的应用［7-8］。目前，NOSB-PD 方法中仍存在因零能模式与边界效应等问题导致的计算精度不足的缺陷，且至今仍未有较为一致的解决方案［9］。

为解决PD方法中的零能模式与边界误差问题，首先简介NOSB-PD 模型的基本理论及应用无网格伽辽金格式对该模型的重构；随后，引入PD 微分算子（PDDO）近似，并对比其与RKPM近似间的异同；基于对比结论，建立RKPM-PD耦合算法，并提出适用于该耦合算法的基于增量格式Newmark 算法的隐式迭代流程；最后，采用RKPM-PD耦合算法对若干三维裂纹扩展问题进行模拟分析。

1 近场动力学理论

1.1 非常规态基近场动力学

在键基PD 以及常规态基PD 模型中并没有传统意义上应力、应变的概念，这为近场动力学的应用带来诸多不便。为解决这一问题，一种新的非常规态基近场动力学（Non-ordinary state-based peridynamic，NOSB-PD）方法被提出。在引入应力、应变概念后，不同材料的本构关系可以很方便地应用于近场动力学方法。在物质点xi处，NOSB-PD方法的运动方程为

为将传统本构模型应用于近场动力学框架，NOSB-PD方法通过变形梯度张量F建立起PD理论与传统力学间的联系。在NOSB-PD 模型中，变形梯度张量F被定义为

为充分应用NOSB-PD 方法与传统本构模型相耦合的优势，可在NOSB-PD 方法中通过物质点的应力来定义键的损伤。定义键ξij的最大主应力为键的2 个端点最大主应力的平均值，当键上的最大主应力超过材料容许的最大强度时，该键发生断裂。对于岩石材料，可通过最大拉应力准则及摩尔-库仑准则来确定岩石材料的最大容许强度［10］。

1.2 基于伽辽金格式的NOSB-PD方法重构

对于传统无网格伽辽金格式，在采用节点积分后，其最终方程可表示为

式中：M为质量矩阵；Kˉ为刚度矩阵；P为外荷载向量；U为所有节点的自由度向量。基于变形梯度张量F的求解公式（4），节点应变求解矩阵Bi可表示为

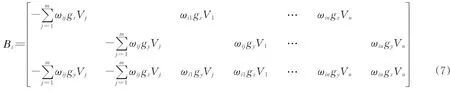
式中：g=[gx gy]T=K ξij；m为xi支撑域内节点xj的数目。

将式（7）代入式（6），可得到式（6）与NOSB-PD方法的全局方程式（3）完全等价的结论［11］。该结果揭示了NOSB-PD 方法实质上是一种伽辽金弱形式方法。基于该结论对NOSB-PD 方法中存在的零能模式与边界误差进行分析可得：①与其他无网格方法类似，NOSB-PD中的零能模式问题也是由于其在伽辽金弱形式下采用了节点积分；②NOSB-PD方法中的节点应变ε是支撑域内最小二乘意义下的计算结果，而最小二乘下的近似一般不会满足δ属性，因此，NOSB-PD方法会在其边界处出现较大的计算误差。

2 近场动力学微分算子近似与重构核函数近似

在非常规态基近场动力学中变形梯度张量F求解方式的基础上，Madenci等［12］提出了一种被称为近场动力学微分算子（PDDO）的理论，该理论同样继承了PD中以积分代替微分的思想，可通过积分形式求得高阶微分算子，可视为式（4）的扩展形式。

2.1 近场动力学微分算子理论

依据多元函数泰勒公式，在d维空间中，标量函数uj在点xj处展开为

其中

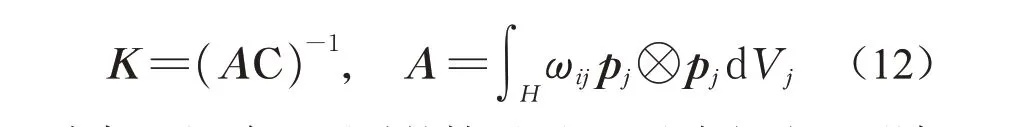
在保证矩阵A可逆的情况下，通过式（11）即可计算出物质点xi上任意维度任意阶导数的PDDO近似。

2.2 二维空间下的PDDO近似

为便于理解，给出二维空间下一阶导数的PDDO近似形式。在二维线性基条件下，式（9）可简化为

式中：N，x，N，y分别为位移一阶导数在PDDO 方法下的形函数。

2.3 RKPM近似函数

基于Liu等［13］研究成果，RKPM近似位移ui可写为

对比PDDO 方案得到的位移近似函数式（14），可以看到PDDO 与RKPM 两方案得到的位移近似函数完全一致。

尽管PDDO 与RKPM 两方案得到的位移近似函数完全一致，但两者对位移导数近似的求解并不一致。RKPM方法中位移导数的近似函数通过对位移近似函数求导得到，即

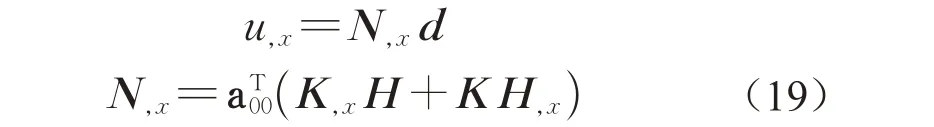
2.4 PDDO近似与RKPM近似的性质对比

Krongauz 与Belytschko［14］指出，为获得最优的数值精度，伽辽金格式中的近似函数应满足一致性条件与积分约束条件。

2.4.1 一致性条件

一般而言，一致性条件总是比较容易满足的。容易证得，PDDO 与RKPM 均满足一致性条件。在一维算例中，11 个固定节点均匀布置在区间［0，10］上，插值点间距0.01，基向量为p=[1x]T，影响函数取为三次样条函数。假设节点位移为y=x，通过插值点计算得到的位移及位移导数的图像如图1所示。从图中可以看出，当基函数一致时，PDDO 与RKPM计算得到的位移近似与位移导数近似具备相同阶数的一致性。

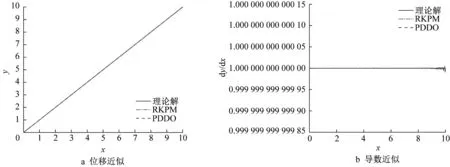
图1 一阶导数为常数时RKPM与PDDO近似的精度比较Fig.1 Comparison of approximate accuracy between RKPM and PDDO at y=x

2.4.2 积分约束条件

积分约束条件也被称作相容性（compatibility）条件，可写为

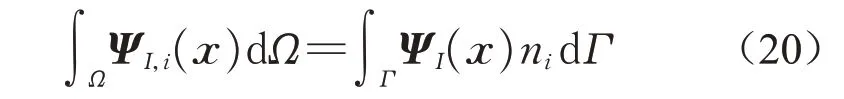
式中：Ψ为伽辽金方法中的位移形函数；Ω为求解域；Γ为求解域边界。对于全局伽辽金格式，积分约束条件是强制性满足的。在RKPM 近似中，位移导数的形函数是通过对位移形函数N进行求导运算而得，因此RKPM 近似天然满足积分约束条件。而PDDO 近似中位移导数形函数N，x与位移形函数N并不一定具有严格的求导关系，前者可能只是形函数导数的一种近似逼近，两者间并不具备严格的导数与原函数的关系。因此，一般情况下，积分约束条件式（20）未必满足。

为充分说明上述条件，取一维杆件进行分析。杆长L=1，节点间距dx=0.1，弹性模量E=1，一维杆件内有均匀分布的应力σ，为保持平衡，杆件左右两端需施加t=σ的外力荷载。显然，模型的平衡方程等价为式（20）。模型内力记为fint，并加以上标PDDO 及RKPM 以示区别；模型所受外力记为fout。计算结果如图2所示，可以看到，fout=fRKPMint≠fPDDOint，即PDDO近似不满足积分约束条件，而RKPM近似满足该条件。

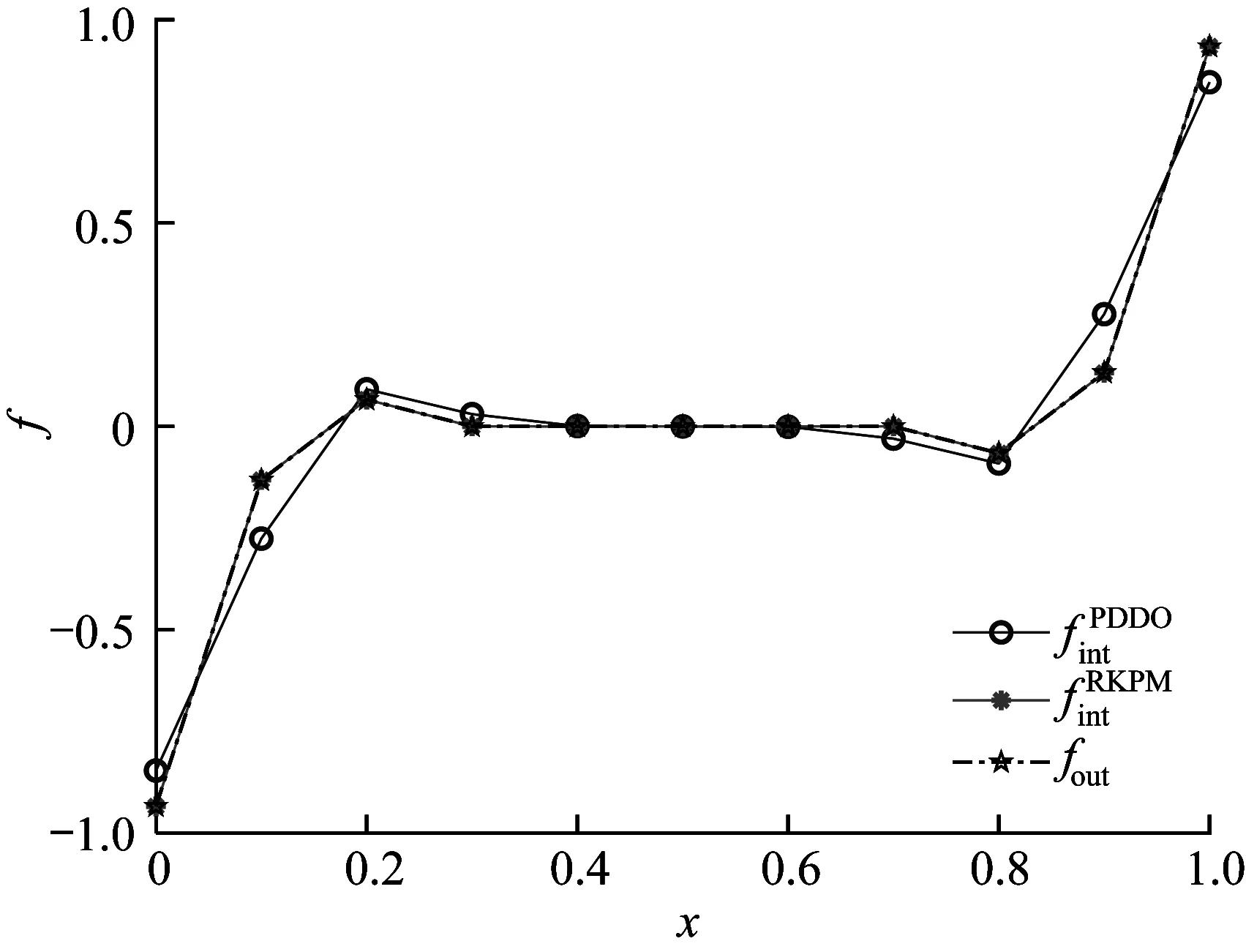
图2 一维杆件内外力分布Fig.2 Distribution of internal and external forces of one-dimensional bar

2.5 不同积分格式下RKPM与PDDO方法计算精度对比

为探究RKPM 与PDDO 方法在不同积分方案下的表现，采用与2.4.2 节相同的体力作用下的一维杆模型，并分别采用节点积分方案及两点高斯积分方案对两近似方法的收敛性进行分析。在不同积分方案下，两方法的位移相对误差收敛性如图3 所示。对比不同积分方案，可以看到：

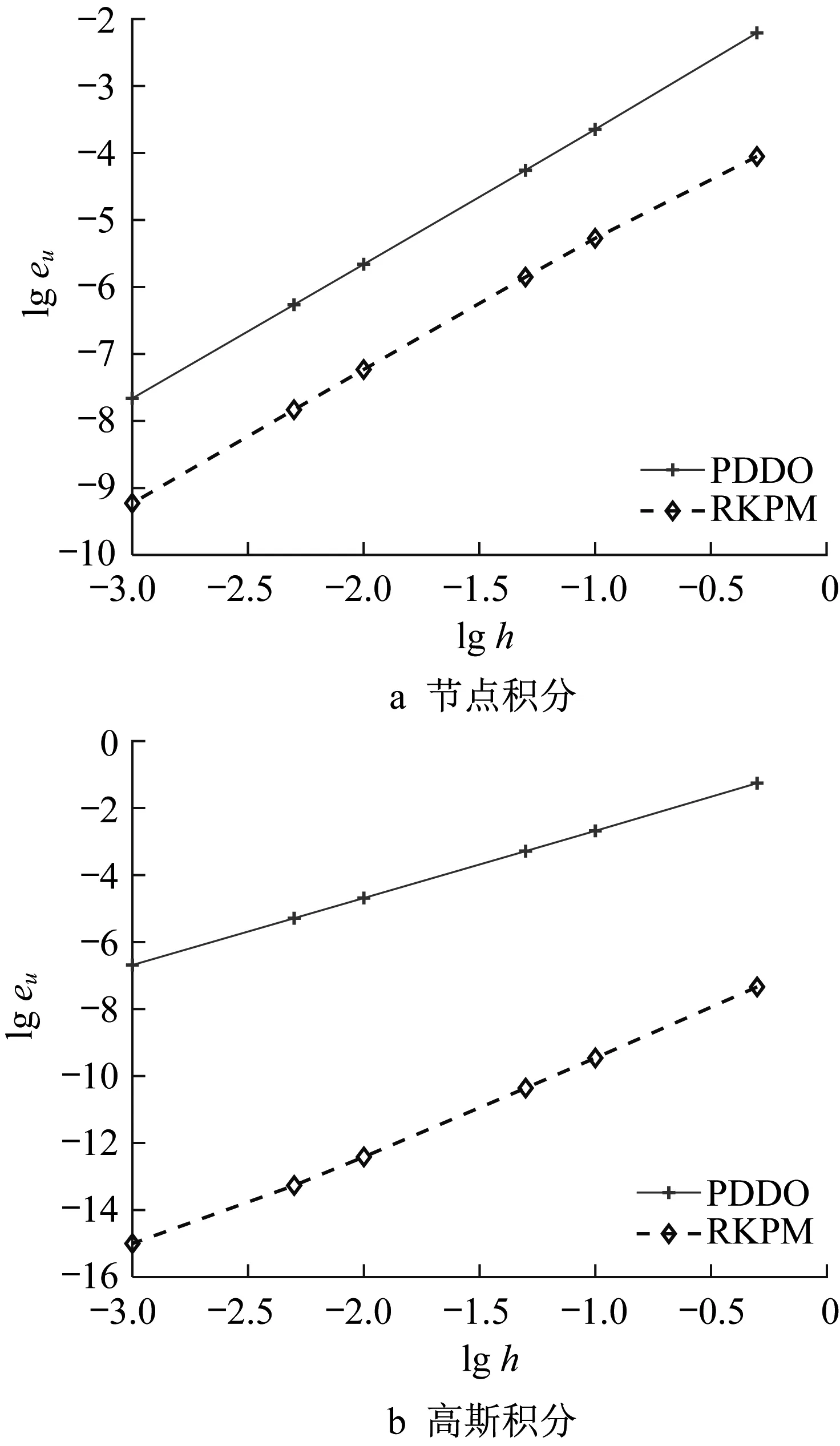
图3 不同积分方案下PDDO与RKPM方法误差对比Fig.3 Error comparison of PDDO and RKPM methods in different integration schemes

（1）对于RKPM 方法而言，采用高斯积分的精度远远高于节点积分。而对于PDDO 方法而言，积分阶次的提高对结果的影响很小。

（2）在不同积分方案下，RKPM方法的精度均比PDDO方法的精度高。但具体而言，在节点积分时，两者的精度比较接近；在采用高斯积分的情况下，两者精度间的差距最为明显。

3 RKPM-PD耦合算法

3.1 概述

传统的无网格方法大多基于断裂力学准则处理裂纹扩展问题。在数值计算中，裂纹的追踪是非常棘手的问题，特别是在三维裂纹扩展问题中，对于裂纹面尖端的动态追踪几乎不可能实现。在PD 方法中，裂纹不再需要显式的追踪，而是通过键上的损伤来表示，当键的临界伸长率超过一定极限时，两点之间的作用键发生断裂。在NOSB-PD 方法中，也可认为当键上的应力超过允许应力时，两点之间的作用键发生断裂。

基于PDDO 近似与RKPM 近似间的异同以及PD键形式的裂纹扩展方案，提出一种RKPM-PD耦合算法，即非裂纹计算部分采用基于RKPM 近似的无网格伽辽金格式以获取更精确的计算精度，裂纹处理部分则采用PD 中基于键形式的损伤模型避免复杂裂纹面的追踪问题。

在RKPM-PD 中，键的断裂准则与裂纹表示方法与NOSB-PD理论一致，其不同之处在于，RKPMPD中除了更新节点与节点间键的状态外，还需要更新积分点与节点间键的状态。具体而言，在节点积分中只需考虑节点与节点间键的状态，但对于背景网格积分（高斯积分），模型中存在积分点与节点两类不同的物质点。按照PD键的概念，算法中高斯点与节点间的键、节点与节点间的键，这2类不同的键均需考虑其断裂与否。

3.2 增量格式Newmark算法

在时间迭代中，采用增量格式的Newmark 算法进行计算。t时刻的Newmark方程可写为

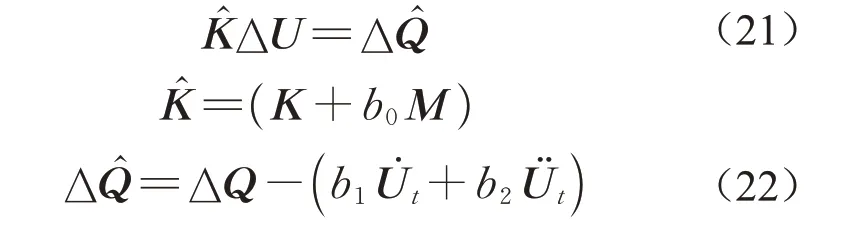
式中：b0、b1、b2均为Newmark 迭代参数。在计算出ΔU后，即可得到Ut+Δt的值，并通过Ut+Δt计算出新的σt+Δt。之后，根据不同的断裂准则，利用t+Δt时刻状态信息判断是否有新的键断掉。对于是否有新键断裂，可分为：

（1）如果当前步中没有新的断键出现，说明t+Δt时刻方程达到平衡，可进入下一步计算。在通过ΔU得到t+Δt时刻的速度及加速度后，进行变量回代，开启下一时步的计算。

（2）如果当前步中有新的断裂出现，说明t+Δt状态并未达到平衡，方程（21）仍需进行迭代计算。此时，对于支撑域内出现新断键的物质点，更新其键的状态，并重新计算该点上的形函数[N]及对应的包含一阶导数的矩阵[B]。在新的断裂出现后，体系内的不平衡力R为

根据式（26）的Ut+Δt重新计算出σt+Δt，并继续判断是否有新的断键出现，如果依然出现新的断键，则返回步骤（2）中继续迭代，直至系统内不再出现新的断键。此时，结束当前时步内的循环，转至步骤（1）中。

4 三维裂纹扩展模拟计算

4.1 含倾斜预制裂纹的三维受拉平板

为体现RKPM-PD方法在处理三维裂纹扩展问题中的优势，考虑如图4 所示模型，其几何尺寸为2m×1m×0.2m，模型下表面（y=0m）固定，上表面（y=2m）受垂直于该平面的拉伸载荷。模型左侧被一裂纹面完全贯穿，裂纹深度为0.2m，并与Oxy平面呈45°夹角。模型节点间距为0.03m，支撑域半径为2 倍节点间距。模型材料力学参数为：弹性模量E=30GPa，泊松比ν=0.2，密度ρ=2 500 kg·m-3。裂纹扩展采用临界伸长率准则，键的临界伸长率sc=0.001。计算采用Newmark 积分，时间步长Δt=0.1ms，载荷Δσ=1×104Pa。

图4 三维含倾斜裂纹受拉平板示意Fig.4 Sketch map of 3D tensile plate with inclined crack

图5中给出预制倾斜裂纹面在受拉平板内的扩展过程。可见，随着拉应力的增大，裂纹首先在倾斜裂纹面的边缘向前扩展，随后，裂纹面从倾斜状态逐渐扭转为竖直状态；之后，裂纹面依然保持垂直于Oxy面的竖直状态沿x方向向前延伸，最终贯穿整个平板。从图中可见，裂纹穿透平板位置约在y=1处，该值近似于倾斜裂纹面y坐标的中心值。另外，在图6 中给出了对应状态下平板内y方向位移的分布，可见，位移分布与裂纹面的扩展状态相吻合。

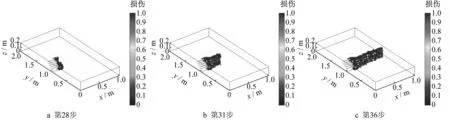
图5 含倾斜裂纹平板在拉伸载荷作用下的裂纹扩展路径Fig.5 Propagations of 3D plate with inclined crack at tensile load

图6 含倾斜裂纹平板在拉伸载荷作用下的纵向位移分布Fig.6 Snapshots of vertical displacement of 3D plate with inclined crack

4.2 含预制裂纹三维巴西圆盘

考虑不同厚度的带预制裂纹的三维巴西圆盘试验。如图7 所示，模型在Oxy平面内的直径为100mm，z方向的厚度为10mm（厚度方向为垂直于纸面的方向）。圆盘上下两端受压，采用Newmark隐式积分方案，时间步长取为Δt=5×10-7s，平均加载速度为每步10-8m。岩石试样力学参数为：弹性模量E=10GPa，泊松比v=0.25，密度ρ=2 500 kg·m-3，抗拉强度T=0.5MPa，黏聚力C=5MPa 以及内摩擦角ϕ=40o。离散模型中平均节点间距h=2mm。在本算例中，预制裂纹长度为30mm，与水平方向呈45o夹角。为探究预制裂纹深度对结果的影响，预制裂纹深度分别取10mm、6mm及2mm。

图7 带预制裂纹的三维巴西圆盘示意Fig.7 Sketch map of 3B Brazilian disk with prefabricated cracks

当预制裂纹深度为10mm 时，预制裂纹在厚度方向完全贯穿平板，模型在z方向完全一致。该算例的裂纹扩展路径如图8所示，可以看到，裂纹扩展路径与二维情况下相一致，裂纹尖端分别向圆盘上下两端的压缩载荷施加处扩展，直至最后裂纹完全贯穿整个圆盘。如图9 所示，该模型采用RKPM-PD的计算结果与在三维NMM方法下的模拟结果［10］及试验结果［15］均保持一致。

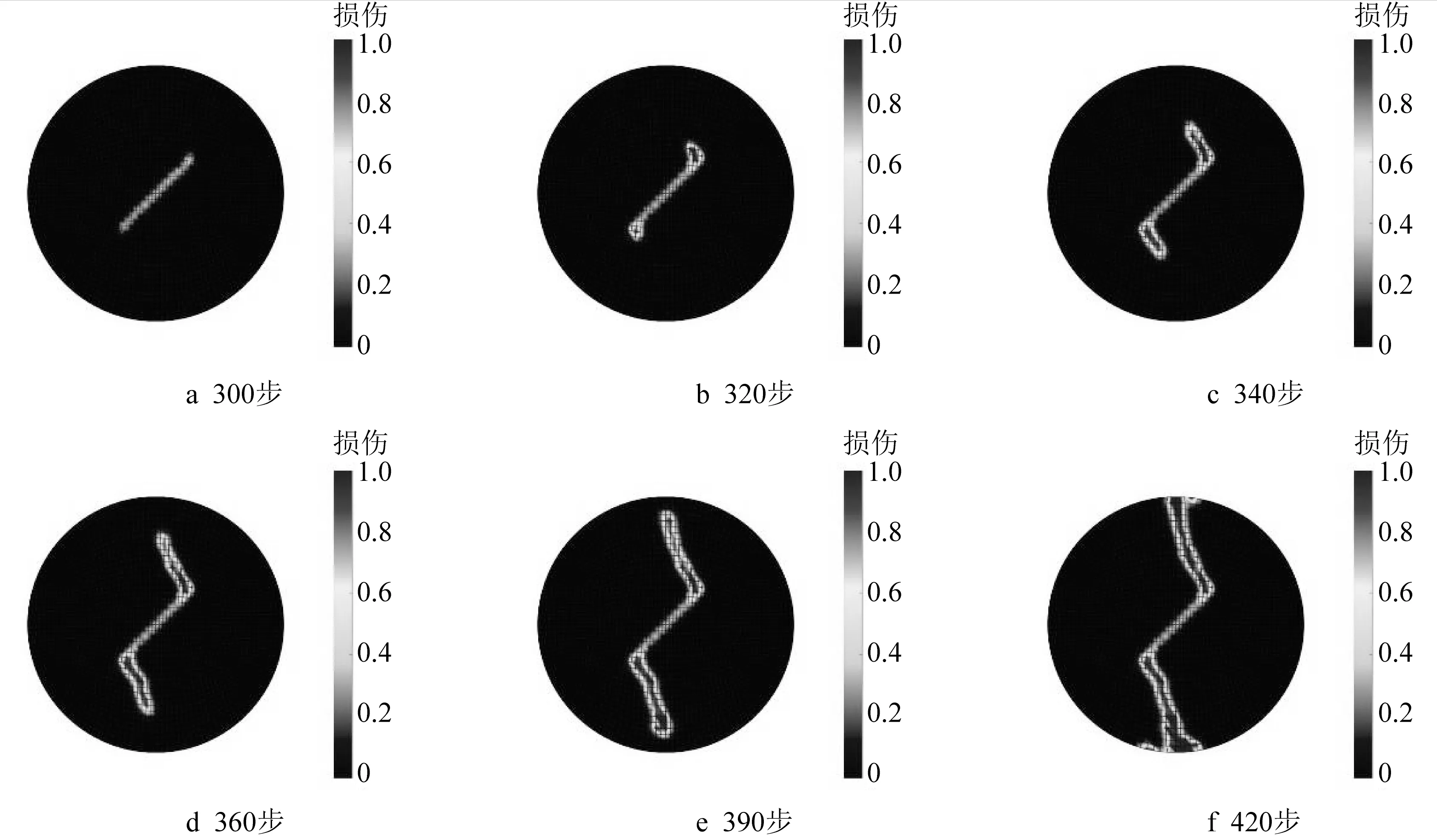
图8 三维巴西圆盘含完全贯穿裂纹的裂纹扩展路径Fig.8 Snapshots of crack path within 3D Brazilian disk with a fully penetrating crack

图9 含完全贯穿裂纹的三维巴西圆盘在NMM方法及室内试验下的裂纹扩展路径Fig.9 Crack path of 3D Brazilian disk with a fully penetrating crack obtained by 3D NMM and experiment results

通过对裂纹完全贯穿试件的分析，证明该方法在三维裂纹问题中的有效性。然后考虑裂纹未完全贯穿的情况，设置裂纹嵌入深度分别为6mm、2mm，其结果分别显示于图10 与图11。为显示裂纹未完全贯穿的情况，对于同一时刻的裂纹扩展结果分别给出其正面图（z=0）与背面图（z=10mm）。其中，裂纹从正面嵌入，终止于圆盘内部，未穿透背面。

图10 三维巴西圆盘含嵌入深度6mm未贯穿裂纹的裂纹扩展路径Fig.10 Snapshots of crack path within 3D Brazilian disk with a penetrating crack (insert depth=6mm)

图11 三维巴西圆盘含嵌入深度2mm未贯穿裂纹的裂纹扩展路径Fig.11 Snapshots of crack path within 3D Brazilian disk with a penetrating crack (insert depth=2mm)

通过对未穿透裂纹的结果分析可知，裂纹首先沿厚度方向扩展，从背面可逐步看到损伤区域的形成；之后，正面与背面的裂纹均沿竖直方向朝两端扩展。对比2 个面的裂纹最终扩展轨迹，可以看到两者大体一致，细微处有所差别。同时可以看到，裂纹切割深度越浅，启裂所需计算步越多。图12给出了3 种不同切割深度下圆盘最顶端3 列节点的轴向平均应力-应变曲线，从图中可以清晰看出，巴西圆盘在表面裂纹（2mm）时所能承受的载荷远远大于深度裂纹（6mm）及完全贯穿裂纹（10mm）时的载荷。