偶极横波远探测在裸眼井及套管井中接收波场的方位响应特征

李杨虎， 唐晓明,3*， 苏远大,3

1 中国石油大学(华东)地球科学与技术学院， 青岛 266580 2 中国石油大学(华东)深层油气重点实验室， 青岛 266580 3 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室， 青岛 266071

0 引言

近年来，偶极横波远探测成像测井技术取得长足发展，其在裂缝、断层、溶蚀孔洞等地质构造的探测中取得了良好的应用效果.Tang(2004)于2004年首次提出了偶极横波远探测成像方法，该方法通过充液井中的偶极声源向地层辐射横波，并在井中接收经反射体反射回来的横波进行井周成像.与常规的单极纵波法相比(Hornby, 1989; 薛梅, 2002; 乔文孝等, 2004; 陶果等, 2008)，偶极横波法具有以下优势：一、偶极声源具有方位灵敏度，采用多分量发射和接收可以确定反射体的走向；二、偶极声源的工作频率为3 kHz左右的低频，因而其径向探测深度更深.此后，国内外学者针对偶极横波远探测技术开展了大量的研究工作，其现已成为非常规油气勘探中寻找油气甜点的利器(Tang and Patterson, 2009; 唐晓明和魏周拓, 2012; 苏远大等, 2014; Tang et al., 2014, 2016; Hirabayashi et al., 2017; 宫昊等, 2018; Bennett, 2019; Lee et al., 2019; Xu et al., 2019; 董经利等, 2020; 古希浩等, 2020; 刘汇鑫等, 2021).

研究井孔对声场的调制作用对偶极横波远探测具有重要意义，包括井内偶极声源在地层中的辐射特性以及井孔对入射波的方位接收响应.对于偶极声源在井外的辐射声场，国内学者已经做了充分研究.Tang等(2014)给出了偶极声源在井外无限大地层中辐射横波的位移远场渐近解及其辐射指向性表达式.在此基础上，曹景记等(2014)和唐晓明等(2019)研究了偶极声源在裸眼和套管井外的横波辐射特征，并证实了在套管井中进行偶极横波远探测的可行性.井孔对入射波的接收响应可分为平面波和球面波入射两种情况，对于平面波入射引起的井内声场的方位响应，人们已经进行了深入研究，见White(1953)、Schoenberg(1986)、Peng等(1993)以及Hirabayashi等(2017)发表的研究成果.然而，声波远探测中入射波场是以球面波的形式向井孔传播，对于球面波入射引起的井内声场的方位响应尚未做深入研究.虽然前人能够对偶极横波远探测的接收声场进行快速模拟(Tang et al., 2014; 许家旗和胡恒山, 2019)，但这些研究中都使用了互易定理来求解井孔的球面波入射响应，该方法主要用于分析井中声源和接收器位置同轴线的情况，不能对实际测井时仪器接收到的方位波场进行有效模拟.针对此，Li等(2021)在虚源法的基础上，结合柱面波展开法(Tang and Cheng，2004)，求解得到了充液裸眼井中偶极横波方位远探测接收声场的解析解，为方位声波远探测的模拟奠定了理论基础.

目前，利用偶极横波远探测进行井周成像或反射体方位识别的相关方法主要是根据井中接收波形的幅度变化特征(Tang and Patterson, 2009; Hirabayashi et al., 2017; 李盛清等, 2020; 许家旗和胡恒山, 2020; Li et al., 2021)，但充液井中远探测波场的方位接收响应还缺乏详尽的理论分析.因此，对偶极横波远探测声场在井内流体中产生的径向位移和声压的方位响应特征进行深入研究具有重要意义.另一方面，基于全球各地油田中套管井的大量存在以及被证实的过套管偶极横波远探测的可行性(唐晓明等, 2019)，本文将裸眼井中远探测声场的方位解析解延展到套管井中，研究了不同胶结情况套管井中接收波场的方位响应特征，并与裸眼井情况进行了对比分析.最后，利用三维有限差分法证实了声场幅值方位响应中的180°反转现象.本文的研究对偶极横波远探测测井时裸眼和套管井中接收声场的方位响应特性有了更为全面的认识，为偶极横波方位远探测的技术发展、仪器研制以及现场解释提供了理论支持.

1 充液井中偶极横波方位远探测接收声场的解析解

图1a给出了当井外存在反射体时，充液裸眼或套管井中偶极声波远探测模拟所用的坐标系.在测井仪器的偶极声源上方环向布置了多组偏心距为e的接收器，其接收横截面如图1b中模型所示.按照不同的声源—接收器组合方式，可模拟不同的测量工作模式，如正交偶极发射—正交偶极接收模式，正交偶极发射—多方位接收模式，本文采用多方位接收模式对井中接收波场的方位响应进行研究.偶极声波远探测包含三个过程，即充液井孔内偶极声源在井外的辐射、井外地质体的反射以及充液井孔对反射波的接收调制.在辐射距离远大于波长的远场辐射条件下，图1a中偶极声源辐射到地层中的SH和SV横波位移势函数和Γ的远场渐近解为(唐晓明和魏周拓, 2012)：

(1)

当辐射横波与地层中的反射体作用后，可将反射回井孔的入射横波波场表示为(Tang et al., 2014, 2016)：

(2)

式中，RD为声源在井外远处的辐射函数，由式(1)的中括号里的部分组成；RF为声波在反射体处的反射系数，可由佐普利兹方程求得(Aki and Richards,

图1 基于虚源法的偶极声波远探测示意图(a)及方位接收井孔截面示意图(b)Fig.1 The schematic model of dipole single-well reflection imaging based on the virtual source analogy (a) and the cross section of borehole receiving configuration using azimuthally spaced off-axis receivers (b)

1980)；S、RD、RF都是关于圆频率ω的函数；D为声波在地层中总的传播距离，其传播路径为一条折线.Li等(2021)通过将远探测声场看作是声源在反射体向外一侧的镜像点的辐射声场，此时声波的传播路径D转化为一条直线，如图1a中所示，从而式(2)中的球面波传播因子可以展开为多极子柱面波叠加的形式(唐晓明和郑传汉, 2004)：

×eik(z-z0)dk，

(3)

将式(3)代入式(2)，对于图1a中所示的偶极声源指向，入射SH和SV横波的位移势函数表达式为：

×cos[n(φ-φ0)],

(4)

其中，上标i表示入射波场；下标SH和SV表示计算声源的辐射函数RD和反射系数RF时应分别对应SH和SV横波.

考虑径向包含多层的井眼模型，假设井壁与地层之间共有N-1圆柱层，其中第m层为固体层，第j层为液体层.当入射横波与井眼相互作用时，根据赫姆霍兹方程，在柱坐标系(r,φ,z)下井内流体中的位移场uf、第j层流体中的位移场uf(j)和第m层固体中散射波的位移场us(m)分别为：

(5)

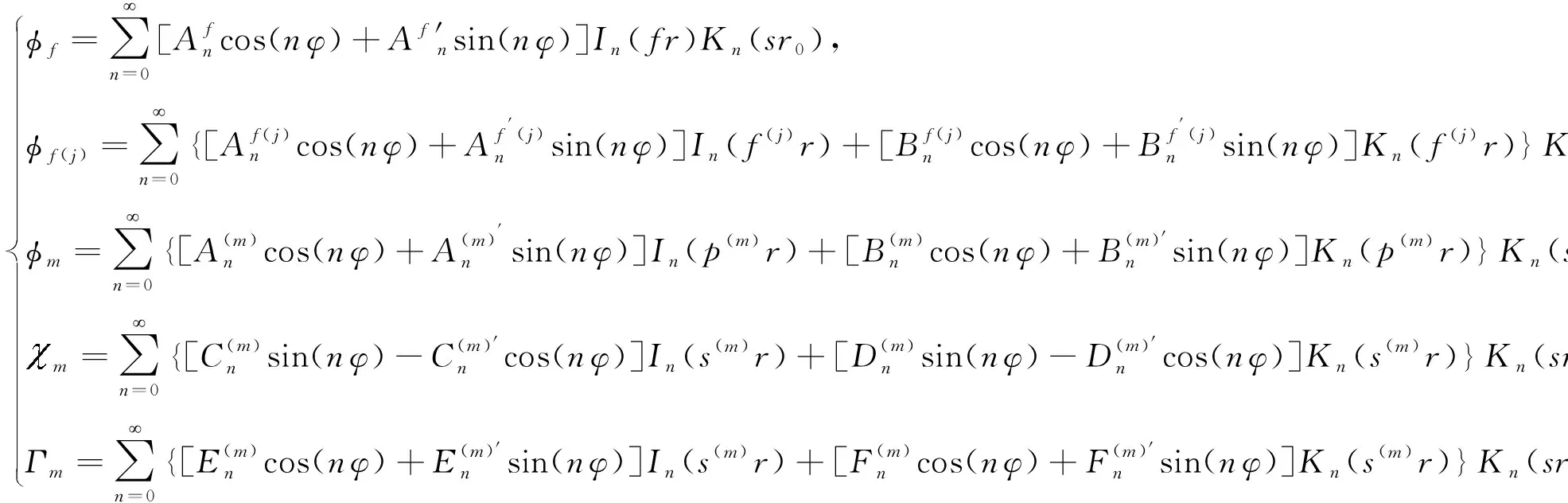
(6)

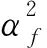
在裸眼井情况下，式(5)中的模型由井内流体和地层两部分组成，此时井壁处的边界条件为：径向位移和正应力连续，环向和轴向的剪切应力为零，表达式为：

(7)

式中，a为井孔半径；上标s和f分别表示地层中的散射波场和流体中的透射波场.

由式(4)、(5)、(6)计算出入射波、散射波和透射波的位移和应力，代入式(7)的边界条件得到两个矩阵方程：

(8)

为了便于描述，将式(8)中方程左侧与井中透射波和地层中散射波有关的矩阵记为矩阵M，右侧与地层中入射波有关的向量分别记为向量b和b′.矩阵M，向量b和b′中的元素表达式详见附录A.

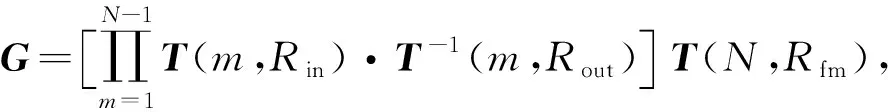
(9)

其中，矩阵元素N11～N41及向量c和c′可由方程(8)中与之相对应的部分将井孔半径置换为套管内径后得到；G矩阵为6×6阶复数矩阵，计算G矩阵所用到的T矩阵的元素表达式详见附录B.

在套管和地层之间添加一流体层来模拟自由套管的情况，此时由井中流体-套管-流体环-地层组成的模型中所包含的3个界面均为流-固界面.与固-固界面不同，对流-固界面的每一个边界条件都要单独进行处理，通过连接边界条件，最后整合得到矩阵方程：

(10)

式中，H为12×12矩阵，d和d′为12×1向量；系数向量中的上标1、2和3表示该振幅系数分别对应套管、流体环和地层介质.矩阵H，向量d和d′中的元素表达式详见附录C.

(11)

其中，ρf为流体密度.对于远场辐射，虚源的径向距离r0远大于弹性波的波长，满足|sr0|≫1的条件，由此可对式(11)中的波数积分运用最速下降方法求解(Tang and Patterson, 2009; Li et al., 2021)，整理得到：

(12)

(13)

式(13)指出，井轴上接收到的流体声压只有单极项(n=0)贡献，而径向位移只有偶极项(n=1)贡献.

综上所述，利用式(12)和式(13)便可计算偶极横波远探测声场在裸眼和套管井情况下所引起的井内流体的径向位移和声压的方位响应.

2 算法对比验证及分析

我们首先利用三维有限差分法验证上述解析解的正确性，采用胶结良好的套管井模型.计算所用的井孔及地层参数如表1所示，其中反射体设为地层1和地层2之间倾角为45°的界面，位于0°方位，虚源的径向距离为10 m.声源上方1 m处共有8个接收器间隔45°环向布置，接收器的偏心距离均为0.035 m.声源采用中心频率为3 kHz的Ricker子波，差分模拟时的空间网格和迭代时间步长分别为0.005 m和0.48 μs.

表1 模型计算参数Table 1 Model parameters for calculation

通过将偶极声源指向y(x)来模拟SH(SV)横波入射，图2和图3给出了对比结果.其中，虚线为有限差分计算的结果，实线为解析解计算的结果.由于有限差分法模拟的是井内和井外的全波波场，而解析解式(12)只模拟了井外的反射波部分，因此图2和图3中只显示了反射横波的到时区间.当声源指向y向时，产生纯SH入射波.从图2中可以看出，无论是井内流体的径向位移(图2a)还是声压(图2b)，采用解析解得到的渐近结果与有限差分模拟的数值结果几乎完全重合，这说明解析解是准确可靠的.图2中也显示出了井中接收波形的方位特征：当接收器指向与反射体走向平行(即90°和270°)时，接收到的径向位移和声压的幅度最大；而当接收器指向垂直于反射面(即0°和180°)时，接收不到径向位移和声压；此外，x轴上下两侧接收到的径向位移和声压的极性均反生反转.上述分析表明，SH横波入射引起的井内流体的径向位移和声压响

图2 SH横波入射引起的井内流体响应的渐近解(实线)和三维有限差分(虚线)的计算结果对比(a) 径向位移； (b) 声压.Fig.2 Comparison of the borehole-fluid response calculated using the analytical solution (solid curves) and the 3D finite-difference method (dashed curves) for SH-wave incidence(a) Radial displacement; (b) Pressure.

应对井外反射体方位的灵敏度高，且两者特征具有较好的一致性，说明在进行远探测时采用反射波中的SH分量更具优势；但该分析也表明了其存在的180°方位不确定性.

当声源指向x向时，利用解析解式(12)计算的是纯SV横波入射，但实际上声源在产生SV横波的同时还会产生P波入射，因此有限差分结果中还包含一些小振幅的P-SV和SV-P转换波(如图3中4.5～5.5 ms所示).尽管如此，图中显示两种方法计算的SV横波反射结果吻合较好.与图2中SH横波的入射结果相比，SV横波入射引起的井内流体的径向位移和声压的方位特征存在较大差异.对于径向位移而言(图3a)，当接收器靠近反射体时接收到的幅度最大，当接收器指向平行于反射面(即90°和270°)时接收到的幅度最小但不为零；y轴左右两侧接收到的位移的极性反生反转.而声压(图3b)则表现出较强的方位性，靠近反射体的接收器接收到的声压幅度最大，并且不同方位接收的声压极性相同.结果表明，在进行远探测时，考虑反射波中的SV分量有助于识别井外反射体的方位.

图3 SV横波入射引起的井内流体响应的渐近解(实线)和三维有限差分(虚线)的计算结果对比(a) 径向位移； (b) 声压.Fig.3 Comparison of the borehole-fluid response calculated using the analytical solution (solid curves) and the 3D finite-difference method (dashed curves) for SV-wave incidence(a) Radial displacement; (b) Pressure.

在套管井复杂模型下所表现出的良好的吻合性，验证了解析解的正确性和普适性.然而，两种方法的计算效率相差很大，为了更准确地模拟接收器的偏心效应以及套管的影响，在三维有限差分建模中必须使用毫米级的网格尺寸，这需要花费数10 h才能完成模拟.相比之下，式(12)的解析解只需要数秒便可以得到准确的结果，为偶极横波方位远探测提供了一种快速高效的模拟方法.

为了进一步详细考察图2和图3中所示波形的方位响应特征，我们增加了接收器的个数并缩小其环向布置间隔.考虑到偶极横波反射成像中存在的180°方位不确定性问题，图4和图5的极坐标图分别给出了SH和SV横波入射时两个相反反射体方位(φ0=0°，180°)的计算结果(图中实线)，其他参数与图2中相同，结果按不同方位接收波形的最大幅值进行归一化处理.如极坐标图中所示，其结果在0°～180°和180°～360°之间具有对称性，因此直角坐标系中只显示了0°～180°的结果.为了对比，同时模拟了当接收器居中时(即位于井轴上)接收的结果，如图中虚线所示.从图4中可以看出，对于SH横波入射，接收器居中时接收到的流体径向位移的方位幅值响应关于90°和270°对称，并且接收不到声压；而当接收器偏心时，接收到的径向位移和声压的幅度最大值所在方位均由90°和270°向靠近反射体一侧偏移.对于SV横波入射(图5)，接收器居中时接收到的流体径向位移和声压的方位幅值响应均关于90°和270°对称，并且声压为一常数值；而接收器偏心时接收到的径向位移的幅度最小值所在方位由90°和270°向靠近反射体一侧偏移，并且靠近反射体的接收器将接收到最大幅值的径向位移和声压.接收器居中时声场响应具有的对称现象可从式(13)中得到，这种对称性正是我们所熟知的180°不确定性.相比之下，接收器偏心接收数据所展示出的非对称性对井外反射体的方位更加敏感，其方位灵敏度有助于解决180°不确定问题.

图4 对于两个相反方位的反射体，SH横波入射引起的井内波场的方位响应(a)、(b) 径向位移； (c)、(d) 声压.Fig.4 The azimuthal response of waveforms inside borehole for SH-wave incidence for the 0° (red) and 180° (black) reflector positions. For comparison, the on-axis result (dashed curves) is also plotted(a) and (b) Radial displacement; (c) and (d) Pressure.

图5 对于两个相反方位的反射体，SV横波入射引起的井内波场的方位响应(a)、(b) 径向位移； (c)、(d) 声压.Fig.5 The azimuthal response of waveforms inside borehole for SV-wave incidence for the 0° (red) and 180° (black) reflector positions. For comparison, the on-axis result (dashed curves) is also plotted(a) and (b) Radial displacement; (c) and (d) Pressure.

接下来我们将重点分析不同接收器偏心距、声源频率和地层类型下裸眼及套管井中接收波场的方位响应特征.

3 裸眼和套管井中接收波场方位响应的影响因素研究

3.1 接收器偏心距对井中接收波场的影响

图6和图7分别给出了裸眼井、自由套管和套管胶结良好情况下，SH和SV横波入射时，不同偏心距接收器接收到的井内流体径向位移和声压的方位幅值响应曲线.计算所用声源的中心频率为3000 Hz，源距为3 m，反射体倾角为60°，位于0°方位，虚源的径向距离为30 m，井孔和地层参数见表1(采用地层1).对于0.001 m的微小偏心距，三种情况下SH和SV横波入射引起的井内流体的径向位移响应相对于90°方位几乎对称，与图4和图5中接收器居中接收的结果相似，此时径向位移的测量结果主要以偶极成分为主，这也说明较小的偏心距对测量结果的影响可以忽略.随着偏心距离从0.001 m增加到0.05 m，当SH横波入射时，裸眼井和自由套管情况下井中接收径向位移和声压的振幅最大值所在方位均逐渐偏离反射体位置，而胶结良好套管井中呈现出偏离方位相反的现象；当SV横波入射时，三种情况下井中接收径向位移的振幅最小值所在方位均逐渐靠近反射体位置，并且其振幅最小值随着偏心距的增加而逐渐增大.此外，SV横波入射时井内声压的振幅最大值所在方位不受接收器偏心距的影响，但受井类型的影响，在裸眼井和胶结良好套管井中，靠近反射体一侧的接收器接收到的声压幅值最大，而在自由套管中则是远离反射体一侧的接收器将接收到最大幅值的声压.值得注意的是，虽然加套管之后井中方位接收响应的变化规律不尽相同，但与裸眼井情况相比，自由套管和套管胶结良好时井中接收波场的方位响应受接收器偏心距的影响更大，说明套管井中的波场响应对井外反射体方位的灵敏度更高.

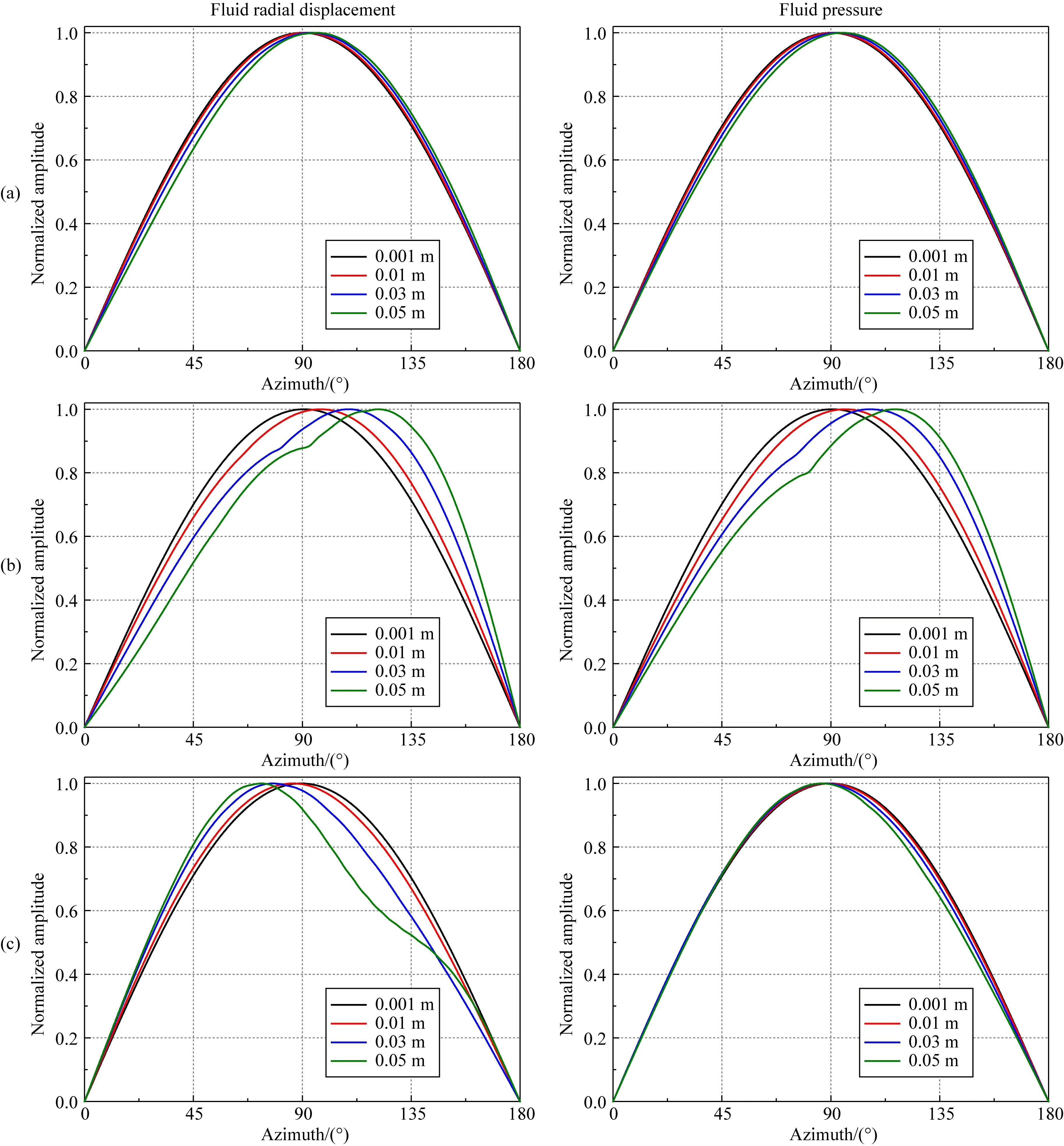
图6 快速地层条件下，SH横波入射时，不同偏心距接收器接收到的井内波场的方位响应(a) 裸眼井； (b) 自由套管； (c) 胶结良好.Fig.6 The azimuthal response of waveforms inside borehole received by receivers with different eccentric distances for SH-wave incidence in the fast formation(a) Open hole; (b) Cased hole with free pipe; (c) Cased hole with good bonding.

图7 快速地层条件下，SV横波入射时，不同偏心距接收器接收到的井内波场的方位响应(a) 裸眼井； (b) 自由套管； (c) 胶结良好.Fig.7 The azimuthal response of waveforms inside borehole received by receivers with different eccentric distances for SV-wave incidence in the fast formation(a) Open hole; (b) Cased hole with free pipe; (c) Cased hole with good bonding.

3.2 声源频率对井中接收波场的影响

图8和图9是声源频率变化时，SH和SV横波入射到裸眼井、自由套管和胶结良好套管井中引起的井内流体的径向位移和声压的方位幅值响应曲线.计算时接收器的偏心距离为0.035 m，其他参数与图6中相同.从图中可看出，对于100 Hz的低频情况，SH和SV横波入射引起的井内流体的径向位移响应相对于90°方位几乎对称.这是因为频率非常低时，声波波长远大于井径，使井孔的调制作用明显减弱，说明低频时可忽略接收器的偏心效应.随着频率从100 Hz增加到5000 Hz，当SH横波入射时，自由套管和胶结良好情况下井中接收径向位移和声压的振幅最大值所在方位均先靠近后偏离反射体位置，但在裸眼井情况下则表现出先靠近后偏离再靠近反射体位置的现象.当SV横波入射时，随着频率增加，三种情况下井中接收径向位移和声压的方位响应较为复杂，其幅度最大值所在方位发生了180°反转.并且某些频率下，声压最大值所在方位既不位于靠近反射体一侧，也不位于远离反射体一侧(比如裸眼井在500 Hz和1000 Hz时，以及胶结良好套管井在500 Hz、1000 Hz和2000 Hz时).上述结果表明，虽然声源频率能够显著改变井内接收波场的方位响应特征，但方位响应随频率呈复杂变化.

图8 快速地层条件下，声源频率不同时，SH横波入射引起的井内波场的方位响应(a) 裸眼井； (b) 自由套管； (c) 胶结良好.Fig.8 The azimuthal response of waveforms inside borehole at different frequencies for SH-wave incidence in the fast formation(a) Open hole; (b) Cased hole with free pipe; (c) Cased hole with good bonding.

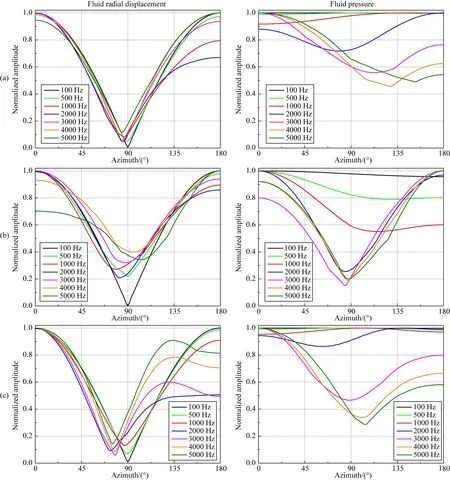
图9 快速地层条件下，声源频率不同时，SV横波入射引起的井内波场的方位响应(a) 裸眼井； (b) 自由套管； (c) 胶结良好.Fig.9 The azimuthal response of waveforms inside borehole at different frequencies for SV-wave incidence in the fast formation(a) Open hole; (b) Cased hole with free pipe; (c) Cased hole with good bonding.

3.3 地层类型对井中接收波场的影响

除了接收器偏心距和声源频率外，地层类型也会影响井中接收波场的方位响应.图10和图11对比了快速和慢速地层条件下，SH和SV横波入射到裸眼井、自由套管和胶结良好套管井中引起的井内流体的径向位移和声压的方位幅值响应.计算时接收器的偏心距为0.035 m，声源主频为3000 Hz，其他参数与图6中相同.从图10中可以看出，当SH横波入射时，裸眼井和自由套管井中流体径向位移和声压的振幅最大值所在方位在快速地层条件下均由90°向远离反射体一侧偏移，而在慢速地层中均向靠近反射体一侧偏移，呈现出相反的现象；在快速和慢速地层条件下，胶结良好时的结果均由90°向靠近反射体一侧偏移.当SV横波入射时(图11)，无论在快速还是慢速地层中，三种情况下井中流体径向位移的振幅最小值所在方位的变化趋势相同，均由90°向靠近反射体一侧偏移，并且靠近反射体的接收器将接收到最大幅值的径向位移；相对于快速地层，在慢速地层中三种情况下的声压方位响应均反生180°反转.上述分析表明，当根据井内接收波场的幅值信息对井外反射体进行方位识别时，需要考虑地层性质的影响.

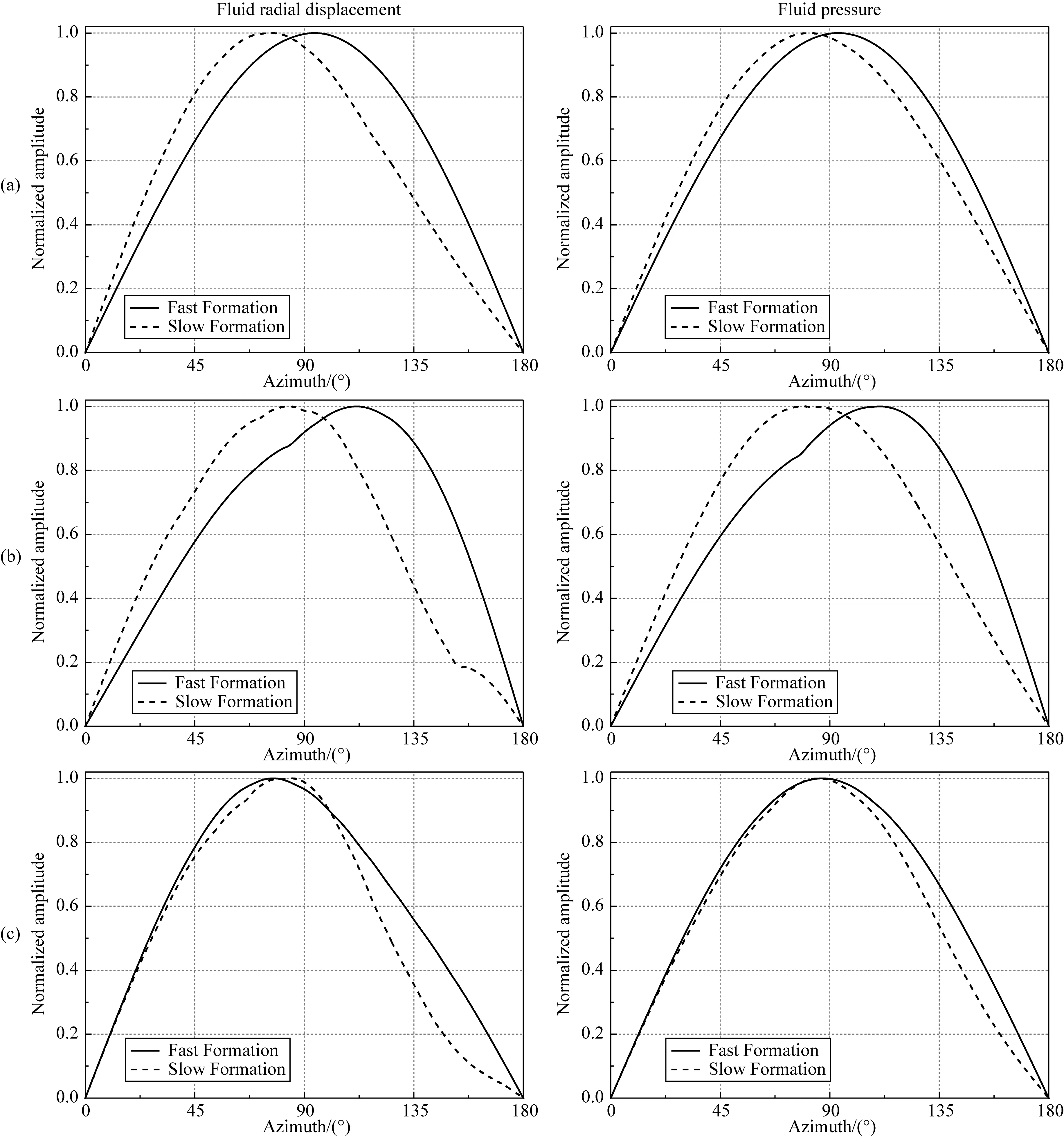
图10 快速和慢速地层条件下，SH横波入射引起的井内波场的方位响应(a) 裸眼井； (b) 自由套管； (c) 胶结良好.Fig.10 The azimuthal response of waveforms inside borehole for SH-wave incidence in the fast and slow formations(a) Open hole; (b) Cased hole with free pipe; (c) Cased hole with good bonding.

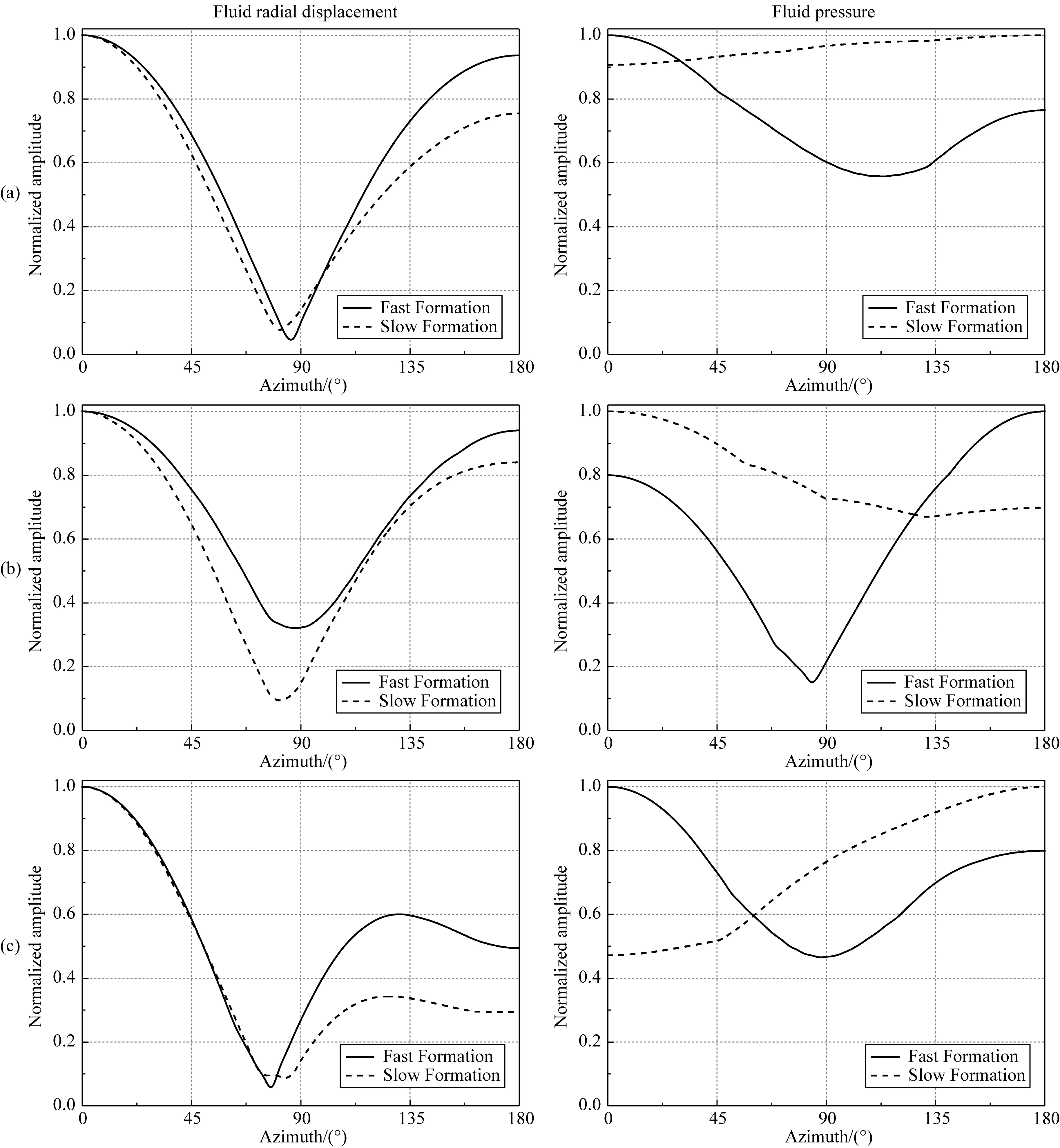
图11 快速和慢速地层条件下，SV横波入射引起的井内波场的方位响应(a) 裸眼井； (b) 自由套管； (c) 胶结良好.Fig.11 The azimuthal response of waveforms inside borehole for SV-wave incidence in the fast and slow formations(a) Open hole; (b) Cased hole with free pipe; (c) Cased hole with good bonding.

4 井中声场方位幅值响应反转现象的正确性验证

上一节研究了偶极横波远探测在裸眼和套管井中接收波场的方位响应特征，我们注意到对于不同的模型参数，井中接收波场的方位幅值特征存在较大差异，在某些情况下甚至会出现相反的现象，过去文献中鲜有类似报道.为了证实这一现象，以SV横波入射到裸眼井中为例，进一步通过三维有限差分法模拟不同频率下井中接收波场的方位响应特征.差分模拟时声源上方共有32个接收器等间隔环向布置，其他参数与图3中相同.考虑声源频率为1500 Hz和4000 Hz两种情况，三维有限差分的计算结果分别如图12中圆圈和三角形标记所示，其中图12a、b分别为流体径向位移和声压的方位响应.为了对比，图中同时给出了利用式(12)得到的解析结果(实线和虚线).从图中可以看出，无论频率为1500 Hz还是4000 Hz时，两种方法计算得到的流体径向位移和声压的方位响应结果均吻合较好.此外，在不同频率下，两种方法均显示出了相反的结果：当频率为1500 Hz时，靠近(远离)反射体一侧的接收器接收到的径向位移(声压)幅值最大；而当频率为4000 Hz时，则是远离(靠近)反射体一侧的接收器将接收到最大幅值的径向位移(声压).三维有限差分计算结果证实了方位幅值响应存在180°反转现象，指示利用井中接收波场幅值特征进行井外反射体方位识别时需要考虑接收器偏心距、声源频率和地层性质等因素的影响，这对于仪器研制和现场解释具有重要的指导意义.

图12 快速地层条件下，声源频率为1500 Hz和4000 Hz时，SV横波入射引起的井中接收波场的方位响应(a) 径向位移； (b) 声压.为了对比，同时给出了渐近解(曲线)和三维有限差分(标记)的计算结果.Fig.12 The azimuthal response of waveforms inside borehole at frequencies 1500 Hz and 4000 Hz for SV-wave incidence in the fast formation(a) Radial displacement; (b) Pressure. The curves and circles are calculated using analytical (curves) and 3D finite-difference (markers) modeling, respectively.

5 结论

本文采用解析法和三维有限差分法对偶极横波远探测在裸眼和套管井中接收波场的方位响应特征进行了研究，得到以下认识和结论：

(1)结合虚源和球面波的柱面波展开，采用最速下降法得到了充液裸眼和套管井中偶极横波方位远探测接收波场的渐近解析解.通过解析法和三维有限差分法对套管井中方位接收波场的模拟对比，验证了渐近解的正确性和普适性.

(2)SH横波入射引起的井内流体的径向位移和声压的方位响应特征具有较好的一致性，而SV横波入射时二者特征却存在较大差异.值得注意的是，SV横波入射时，井内波场的方位幅值响应对井外反射体位置具有唯一性，即在常用偶极测井频率下，靠近或远离反射体的接收器接收到的波形幅值最大.这表明在进行声波远探测成像解释时，考虑井内接收信号中的SV分量有助于识别井外反射体的方位，但需要注意接收换能器记录的信号类型(径向位移/声压)的不同响应.

(3)偶极横波远探测井内接收波场的方位响应特征受井眼环境、接收器偏心距、声源频率和地层性质等多个因素的影响，在不同参数下方位幅值响应甚至会出现反转现象，渐近解析解和三维有限差分数值解的结果对比证实了这一现象，实际数据解释时需要考虑这些因素的影响.此外，在影响井内声场方位响应的众多因素当中，最重要的主控因素是接收器偏心距.正是由于偏心接收才有文中不同于偶极180°对称性的变化现象(即图4—图12所示结果)，其物理实质是声场在偏离井心位置上的复杂三维变化；而居中时三维变化就降到了二维，复杂性减少但(180°)对称现象出现.

(4)相对于裸眼井，套管井中接收波场的方位响应对井外反射体位置的灵敏度更高，受接收器偏心距、声源频率和地层性质的影响也更大，说明在套管井中进行偶极横波方位远探测更有利于井外反射体的方位识别.

(5)现有的偶极横波测井仪将仪器两侧的接收换能器记录的信号之差作为测量信号，此时无论换能器记录的是流体径向位移还是声压，相减后的测量信号中都主要包含偶极成分，可以得到反射体的走向信息；接收器的偏心效应包含了反射体的倾向信息，有助于解决偶极横波远探测方位的180°不确定性问题.

附录A 裸眼井情况下矩阵方程中的元素表达式

矩阵M中各元素的具体表达式为：

M11=-nIn(fa)/a-fIn+1(fa),

M12=nKn(pa)/a-pKn+1(pa),

M13=nKn(sa)/a,

M14=ik[nKn(sa)/a-sKn+1(sa)],

M21=ρfω2In(fa),

M22=2ρβ2[(n2-n)Kn(pa)/a2+pKn+1(pa)/a]

+ρ(2k2β2-ω2)Kn(pa),

M23=2nρβ2[(n-1)Kn(sa)/a2-sKn+1(sa)/a],

M24=2ikρβ2{[(n2-n)/a2+s2]Kn(sa)

+sKn+1(sa)/a},

M31=0,

M32=2nρβ2[(1-n)Kn(pa)/a2+pKn+1(pa)/a],

M33=-ρβ2{[2(n2-n)/a2+s2]Kn(sa)

+2sKn+1(sa)/a},

M34=2iknρβ2[(1-n)Kn(sa)/a2+sKn+1(sa)/a],

M41=0,

M42=2ikρβ2[nKn(pa)/a-pKn+1(pa)],

M43=iknρβ2Kn(sa)/a.

M44=-(s2+k2)ρβ2[nKn(sa)/a-sKn+1(sa)].

(A1)

向量b和b′中的元素由于入射波的类型不同而有所区别.当SH横波入射时，向量b和b′中各元素的具体表达式为(省略公共因子S(ω)·RDSH(ω)·RFSH(ω))：

b1=-nεnIn(sa)sin(nφ0)/a,

b2=-2nεnρβ2[(n-1)In(sa)/a2

+sIn+1(sa)/a]sin(nφ0),

b3=εnρβ2{[2(n2-n)/a2+s2]In(sa)

-2sIn+1(sa)/a}sin(nφ0),

b4=-iknεnρβ2In(sa)sin(nφ0)/a,

b′1=nεnIn(sa)cos(nφ0)/a,

b′2=2nεnρβ2[(n-1)In(sa)/a2+sIn+1(sa)/a]

×cos(nφ0),

b′3=-εnρβ2{[2(n2-n)/a2+s2]In(sa)

-2sIn+1(sa)/a}cos(nφ0),

b′4=iknεnρβ2In(sa)cos(nφ0)/a.

(A2)

当SV横波入射时，向量b和b′中各元素的具体表达式为(省略公共因子S(ω)·RDSV(ω)·RFSV(ω))：

b1=-ikεn[nIn(sa)/a+sIn+1(sa)]cos(nφ0),

b2=-2ikεnρβ2{[(n2-n)/a2+s2]In(sa)

-sIn+1(sa)/a}cos(nφ0),

b3=-2iknεnρβ2[(1-n)In(sa)/a2-sIn+1(sa)/a]

×cos(nφ0),

b4=εn(s2+k2)ρβ2[nIn(sa)/a+sIn+1(sa)]cos(nφ0),

b′1=-ikεn[nIn(sa)/a+sIn+1(sa)]sin(nφ0),

b′2=-2ikεnρβ2{[(n2-n)/a2+s2]In(sa)

-sIn+1(sa)/a}sin(nφ0),

b′3=-2iknεnρβ2[(1-n)In(sa)/a2

-sIn+1(sa)/a]sin(nφ0),

b′4=εn(s2+k2)ρβ2[nIn(sa)/a+sIn+1(sa)]sin(nφ0)，

(A3)

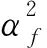
附录B 套管井(胶结良好)情况下T矩阵的元素表达式

T矩阵的元素表达式为：

T11=nIn(pR)/R+pIn+1(pR),

T12=nKn(pR)/R-pKn+1(pR),

T13=nIn(sR)/R,

T14=nKn(sR)/R,

T15=ik[nIn(sR)/R+sIn+1(sR)],

T16=ik[nKn(sR)/R-sKn+1(sR)],

T21=-nIn(pR)/R,

T22=-nKn(pR)/R,

T23=-nIn(sR)/R-sIn+1(sR),

T24=-nKn(sR)/R+sKn+1(sR),

T25=-iknIn(sR)/R,

T26=-iknKn(sR)/R,

T31=ikIn(pR),

T32=ikKn(pR),

T33=0,

T34=0,

T35=-s2In(sR),

T36=-s2Kn(sR),

T41=2ρβ2[(n2-n)In(pR)/R2-pIn+1(pR)/R]

+ρ(2k2β2-ω2)In(pR),

T42=2ρβ2[(n2-n)Kn(pR)/R2+pKn+1(pR)/R]

+ρ(2k2β2-ω2)Kn(pR),

T43=2nρβ2[(n-1)In(sR)/R2+sIn+1(sR)/R],

T44=2nρβ2[(n-1)Kn(sR)/R2-sKn+1(sR)/R],

T45=2ikρβ2{[(n2-n)/R2+s2]In(sR)

-sIn+1(sR)/R},

T46=2ikρβ2{[(n2-n)/R2+s2]Kn(sR)

+sKn+1(sR)/R},

T51=2nρβ2[(1-n)In(pR)/R2-pIn+1(pR)/R],

T52=2nρβ2[(1-n)Kn(pR)/R2+pKn+1(pR)/R],

T53=-ρβ2{[2(n2-n)/R2+s2]In(sR)

-2sIn+1(sR)/R},

T54=-ρβ2{[2(n2-n)/R2+s2]Kn(sR)

+2sKn+1(sR)/R},

T55=2iknρβ2[(1-n)In(sR)/R2-sIn+1(sR)/R],

T56=2iknρβ2[(1-n)Kn(sR)/R2+sKn+1(sR)/R],

T61=2ikρβ2[nIn(pR)/R+pIn+1(pR)],

T62=2ikρβ2[nKn(pR)/R-pKn+1(pR)],

T63=iknρβ2In(sR)/R,

T64=iknρβ2Kn(sR)/R,

T65=-(s2+k2)ρβ2[nIn(sR)/R+sIn+1(sR)],

T66=-(s2+k2)ρβ2[nKn(sR)/R-sKn+1(sR)].

(B1)

附录C 套管井(自由套管)情况下矩阵方程中的元素表达式

矩阵H中各元素的具体表达式为(未列出的元素取值为0)：

H11=-nIn(fr1)/r1-fIn+1(fr1),

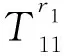
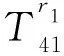
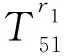
H58=-nIn(fr2)/r2-fIn+1(fr2),

H59=-nKn(fr2)/r2+fKn+1(fr2),

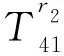
H69=ρfω2Kn(fr2),

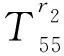
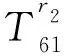
H98=-nIn(fa)/a-fIn+1(fa),

H99=-nKn(fa)/a+fKn+1(fa),

H10,8=ρfω2In(fa),H10，9=ρfω2Kn(fa),

(C1)

其中，r1和r2分别为套管的内半径和外半径；T的右上标表示计算时半径R的取值.

根据入射波类型的不同(即SH或SV横波入射)，向量d和d′中的元素也有所区别，其各元素的具体表达式为(未列出的元素取值为0)：

d9=b1,d10=b2,d11=b3,d12=b4,

d′9=b′1,d′10=b′2,d′11=b′3,d′12=b′4.

(C2)

附录D 井轴处的声压和径向位移

首先求解井轴处的声压，第一类变型贝塞尔函数具有如下性质：

(D1)

其中，n为阶数.接收器位于井轴时，式(12)中的r=0，由式(D1)可知，此时声压的多极响应中只有n=0这一项有值，其余全为0，表达式为：

(D2)

求解井轴处的径向位移时，需要用到第一类变型贝塞尔函数的递推公式：

(D3)

其中，x为变量.将式(D3)代入式(12)的径向位移表达式中可得：

×[In-1(f0r)+In+1(f0r)].

(D4)

n=0时，式(D4)中将出现负数阶贝塞尔函数，可根据整阶贝塞尔函数的奇偶性进行计算，公式为：

I-n(x)=In(x).

(D5)

令式(D4)中的r=0，将式(D1)和(D5)代入式(D4)中，得到井轴处的径向位移为：

(D6)

式(D6)表明，井轴处的径向位移只有偶极项(n=1)贡献.