非椭圆扩展目标联合跟踪与分类算法*

占荣辉，王丽萍, 2

(1. 国防科技大学 电子科学学院， 湖南 长沙 410073； 2. 中国人民公安大学 侦查学院， 北京 100038)

跟踪和分类是目标监视系统中的两项基本任务，分别对应状态估计和目标类别判断，且两者是相互联系、相互影响的。例如，目标状态估计的结果可以作为目标分类的依据，而与目标类别相关的运动模型可以提高目标状态估计精度。联合跟踪与分类(joint tracking and classification, JTC)算法将两者放在统一框架下进行处理，能有效提高系统跟踪精度和分类的准确性[1-12]。目前，JTC算法主要有两类：基于运动学信息的JTC算法[2-5]和基于特征观测的JTC算法[6-12]。基于运动学信息的JTC算法主要利用目标的机动性，如文献[2-5]利用加速度和速度包络信息对目标进行JTC处理，该类算法受限于目标机动模式特征的影响，当待分类的目标运动特性有重叠时很难奏效。基于特征观测的JTC算法通常需要利用属性传感器给出的目标特征信息，如文献[6-10]利用属性量测信息，建立目标位置与属性量测的联合似然函数，实现目标的JTC处理；文献[11-12]提出利用电子支援设备(electronic support measure, ESM)的属性量测信息进行目标分类。很明显，基于特征观测的JTC算法需要额外的传感器支持，增加了系统的复杂度。

随着传感器分辨率的提高，一个目标将占据多个分辨单元，从而产生多个量测，这种情况下的目标被称为扩展目标[13-14](extended target, ET)。目前，扩展目标跟踪(extended target tracking, ETT)算法主要分为两大类：基于随机矩阵模型[15-17](random matrix model, RMM)和基于随机超曲面模型[18-20](random hypersurface model, RHM)。基于RMM的ETT方法用椭圆形状描述目标扩展状态，利用矢量x将目标运动状态建模成高斯分布N(x;m,P)，通过一个对称正定(symmetric positive definite, SPD)矩阵X将目标空间扩展状态建模成逆威沙特分布IW(X;v,V)。基于RHM的ETT方法将目标运动学状态和空间扩展状态建模为一个高维的矢量，并假定量测源位于形状边界圈定的范围之内。基于不同类型的随机超曲面，目标的空间扩展状态可建模为椭圆形[19]和星凸形[20]。

相比于传统基于点目标的JTC算法，扩展目标的空间扩展形态可直接作为目标分类的依据。文献[21]提出了一种基于RMM的扩展目标JTC算法，但该算法没有考虑杂波、多目标情况。为了解决有杂波情况下的单扩展目标JTC问题，文献[22]提出了一种基于伯努利滤波器的单扩展目标JTC算法，文献[23-24]和文献[25]则给出了基于概率假设密度滤波器和势均衡多目标多伯努利滤波器的多扩展目标JTC算法。在现有基于RMM的JTC算法中，统一将目标建模为椭圆形状，在分类过程中只用到了粗略的尺寸(长、短轴大小)信息。

事实上，扩展目标的空间扩展状态包括形状、尺寸和旋转方向。当目标尺寸相近时，基于RMM的JTC算法无法对目标进行准确的分类。目标扩展状态描述越详细，越有利于目标进行准确分类。文献[26]提出了一种非椭圆形状的扩展目标JTC算法，该算法基于RMM利用多个子椭圆对目标形状进行描述，但算法假设子椭圆的个数是固定、已知的，且子椭圆个数随目标形状复杂度的增加而增多，因此算法运算量大、实时性较差。

基于星凸RHM的ETT算法将目标扩展状态建模为星凸形状，能更好地描述目标空间扩展形态的细节信息。鉴于此，本文采用星凸RHM对扩展目标状态建模，提出了一种基于RHM的非椭圆扩展目标(non-ellipsoidal ET) JTC算法，称为NEET JTC。为解决高维状态量和强非线性观测模型带来的算法实现难题，文中将目标状态分解为两个维度较低的运动学状态和扩展状态，建立了目标扩展状态与量测的似然函数，利用粒子滤波(particle filter, PF)实现了目标类别概率的递推处理，并通过典型仿真实例验证了所提算法的有效性及相对于传统算法的性能优势。

1 基于星凸RHM的ETT算法

假定从目标中心到集合S中任意一点的连线仍属于集合S，则这个集合S是星凸的。图1给出了用径向函数r(φ)描述的星凸形状。

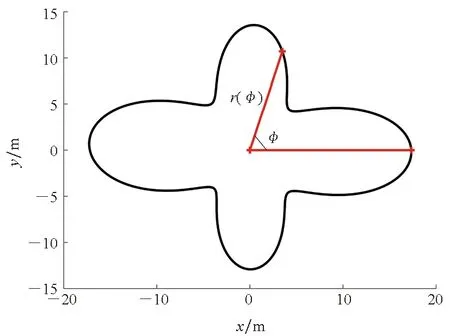
(a) 星凸形状(a) Star-convex shape

在k时刻，目标的径向函数r(φk)是方位角为φk∈[0,2π)的边界点到目标中心的距离函数。采用nF阶傅里叶级数对径向函数r(φk)进行展开得

Γ(φk)≜[1,cos(φk),sin(φk),…,
cos(nFφk),sin(nFφk)]

(2)

(3)

基于星凸RHM的ETT算法其观测模型[21]可表示为

zk,l=yk,l+vk,l

(4)

其中，zk,l为k时刻目标产生的第l个量测，yk,l为该量测的量测源，vk,l为量测噪声，H为观测矩阵，sk,l∈[0,1]为缩放因子，e(φk,l)≜[cos(φk,l),sin(φk,l)]T为单位矢量。

(5)

因此，基于星凸RHM的ETT算法中观测模型的最终形式为

0=h*(xk,sk,l,vk,l,zk,l)

(6)

式中，观测模型h*(·)将目标状态xk、量测噪声vk,l、缩放因子sk,l和目标量测zk,l映射为伪量测0。

与式(6)对应的观测模型具有高度非线性特点，文献[20]给出了基于不敏卡尔曼滤波(unscented Kalman filter, UKF)的实现形式，文献[27]则给出了基于PF的实现形式。 对于UKF，当系统非线性程度较高时，算法的估计精度会下降；对于PF，由于目标的状态被建模为一个高维的状态矢量，需要大量的粒子才能保证较高的估计性能，因此算法复杂度高、实时性较差。

2 NEET JTC算法原理

2.1 目标类别先验信息表征

假设监视区域有nc种不同类别的目标，其类别标签为c∈{1,2,…,nc}。 JTC处理是指同时实现对目标状态xk的估计和类别c的判断，为此需获得目标的概率密度-质量函数p(xk,c|Yk)。 由条件概率公式可得

p(xk,c|Yk)=p(xk|c,Yk)p(c|Yk)

(7)

式中，Yk为到k时刻为止的累积量测，p(xk|c,Yk)表示与类别相关的目标状态概率密度函数，p(c|Yk)表示目标属于类别c的概率。

2.2 先验信息与扩展状态的关系构建

假设目标的轴向与速度方向一致，目标类别c的一个量测源yl对应的方位角为θc，图2给出了量测源yl旋转前后的位置。 若k时刻目标的旋转角度为θk，量测源yl在k时刻所在的位置为yk,l，

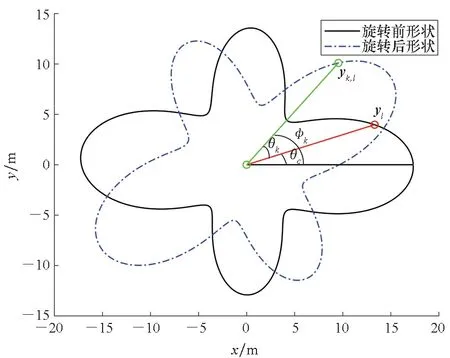
图2 旋转前后的量测源位置Fig.2 Measurement position before and after rotation

则其对应的方位角为

φk=θk+θc

(8)

同一个量测源的径向距离不随目标的旋转而发生变化，即

r(φk)=r(θc)

(9)

其中，

(10)

根据式(8)中的角度关系，可得r(θc)关于θk和φk的傅里叶级数展开形式

(11)

其中，

(12)

r(φk)可整理成两个矢量相乘的形式，即

r(φk)=[1,cos(φk),sin(φk),…,

(13)

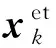
(14)

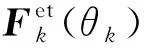
(15)

(16)

利用式(14)所构建的关系，即可将目标类别先验信息集成到滤波过程中，实现扩展目标JTC处理。

2.3 状态估计与类别更新

由前文可知，在基于星凸RHM的ETT算法中，虽然观测模型具有高度非线性，但对于目标运动学状态则可转化为式(17)所示的线性观测模型。

(17)

在本文所提NEET JTC算法中，目标的量测仅用来更新目标的运动学状态，目标的扩展状态通过式(14)给定的关系进行更新。 由条件分布可知，与目标类别相关的概率密度函数p(xk|c,Yk)可分解为两个因式相乘的形式

(18)

目标的运动学状态估计仅受量测的影响，由贝叶斯定理可知，与目标类别相关的运动状态更新过程为

(19)

其中，

(20)

(21)

目标类别概率p(c|Yk)的更新可通过贝叶斯定理得到，即

(22)

其中，

(23)

(24)

(25)

式中，δ(·)表示狄拉克函数。

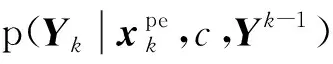
(26)

(27)

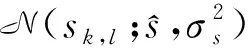
(28)

其中，

由式(22)、式(25)和式(28)可得到目标类别概率p(c|Yk)的更新公式为

p(c|Yk)

(29)

3 NEET JTC算法的实现过程

与基于星凸RHM的ETT算法类似，本文所提NEET JTC算法其递推过程也由预测和更新两步组成。

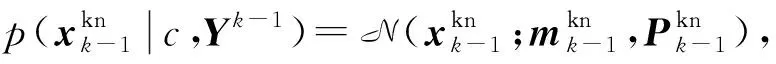
(30)

(31)

vk|k-1=2d+2+e-t/τ(vk-1-2d-2)

(32)

(33)

其中，t表示采样间隔，τ为衰减系数，d为描述目标运动空间的维度。

(34)

(35)

(36)

(37)

(38)

(39)

vk=vk|k-1+nk

(40)

(41)

(42)

(43)

3)目标状态融合与输出：由全概率定理可得，k时刻目标的状态p(xk|Yk)为

(44)

4 仿真实验

为了验证所提NEET JTC算法对目标状态估计的有效性、对目标类别判断的准确性，以及在性能方面的优势，将其与文献[21]中基于RMM的JTC算法(记作JTC-RMM)、文献[27]中基于PF实现的ETT算法(记作ETT-PF)及文献[20]中基于UKF的ETT算法(记作ETT-UKF)进行比较。

为了全面测试所提算法的性能，考虑两个不同的仿真场景。由于目标的运动属性也可作为目标分类的依据，为避免这种影响，设置仿真场景1，用来比较NEET JTC和JTC-RMM算法对匀速直线运动目标进行跟踪和分类的实验结果，验证两种算法对尺寸相近、形状不同目标的分类效果。在目标进行机动的仿真场景2中，比较NEET JTC、ETT-PF和ETT-UKF算法对目标状态估计的结果，验证JTC算法相对于单纯的目标跟踪算法(无分类功能)在状态估计精度方面的优势，同时给出目标类别概率，说明在目标机动情况下所提NEET JTC算法仍能准确进行目标分类。最后，通过对算法运行时间开销进行评估，比较所提NEET JTC与ETT-PF、ETT-UKF的算法复杂度。

每个仿真场景中，仅有一个未知具体类型的目标存在，目标质心的运动轨迹如图3所示。场景1和场景2中采样的次数(观测周期数)分别为30和115。场景1中的目标一直做匀速直线运动。场景2中目标在第1～30、52～72和95～115时刻做匀速直线运动，第31～51和73～94时刻做转弯率为2π/180 rad的匀转弯运动。

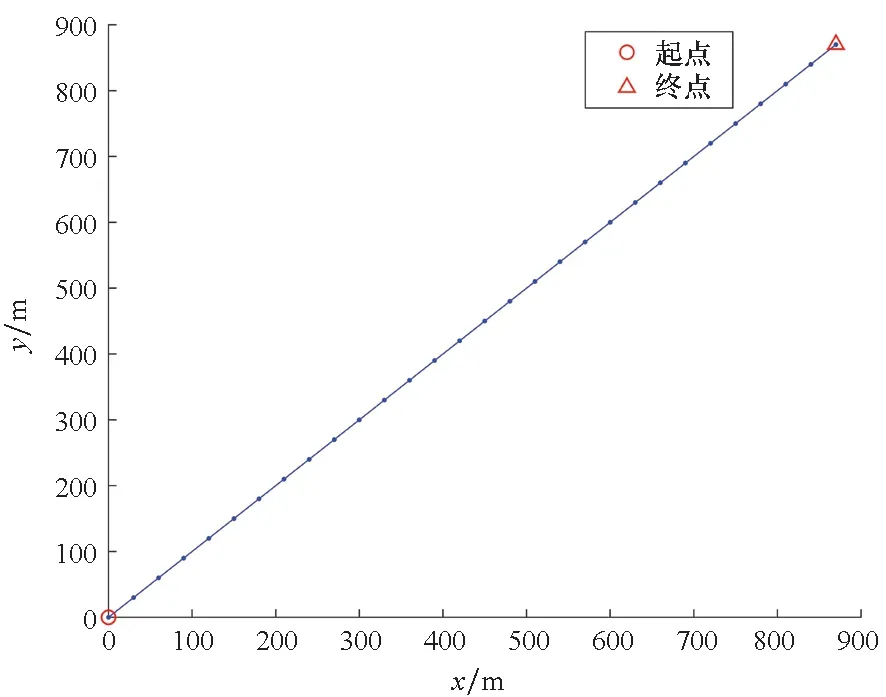
(a) 场景1(a) Scenario 1

在仿真中，分别采用位置的均方根误差(root mean square error, RMSE)和形状的交并比(intersection over union, IOU)来评价算法对目标运动学状态估计和空间扩展状态估计的性能。RMSE越低表示运动学状态估计越准确；IOU的取值范围为0～1，越接近1表示空间扩展状态估计越准确。采用类别概率评价算法对目标分类的性能，若类别概率大于某个阈值，则断定目标属于该类别。

4.1 仿真条件

(45)

(46)

(47)

其中，t=2 s为采样时间间隔(观测周期)，Σ2是加速度方差。

加速度方差Σ2为0.1 m2/s4，量测噪声协方差为R=diag([0.10.1]) m2，缩放因子的均值为2/3、协方差为1/18，傅里叶级数2nF+1=11。在ETT-PF算法中，粒子的个数为20 000。NEET JTC算法中角度α=5π/180 rad，步长Δθ=0.1π/180 rad，因此所用的粒子个数为101。场景中可能出现三种不同类别的目标，类别1的形状是两个正交矩形组成的十字形，尺寸分别为34 m×5 m和20 m×5 m；类别2是半径为20 m的五角星形状；类别3是形状为L的不规则(且非对称)形状，水平矩形的尺寸为22 m×5 m，垂直矩形的尺寸为12.5 m×10 m。作为一种典型的实例，这三种形状可认为是对某固定翼无人机、旋翼无人机、以及受遮挡(仅单侧可见)固定翼无人机模型的简化和近似。三类目标在每个时刻产生的量测个数服从均值为10的泊松分布。与目标类别相关的先验信息通过在目标表面产生1 000个随机量测并基于ETT-UKF算法[20]获得，如图4中红色闭合曲线所示。

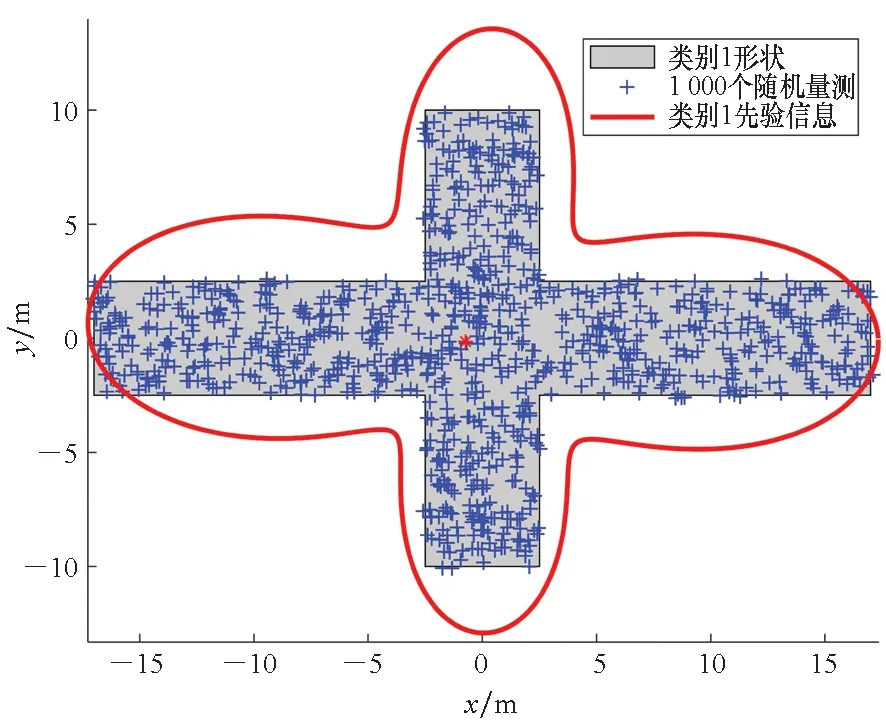
(a) 类别1(a) Class 1

在JTC-RMM算法中，目标的类别先验信息为SPD矩阵，类别1、2和3的先验信息分别为

(48)

(49)

(50)

4.2 仿真结果

4.2.1 场景1实验结果

NEET JTC和JTC-RMM算法对目标状态估计的单次运行结果如图5所示，通过100次蒙特卡洛实验，两种算法对类别1、2和3的目标分类结果分别如图6、图7和图8所示。

(a) 类别1(a) Class 1

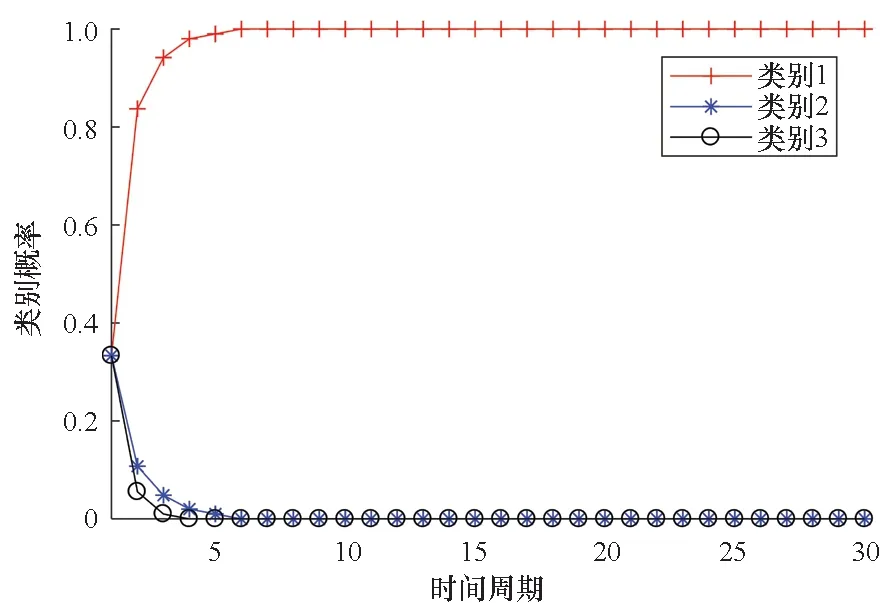
(a) NEET JTC类别概率(a) Class probability obtained by NEET JTC

JTC-RMM算法是基于RMM的算法，将目标空间状态建模为椭圆形状，NEET JTC算法是基于星凸RHM的算法，将目标空间扩展状态建模为星凸形状。由图5可以看出，两种算法都能对扩展目标的运动学状态进行估计，但是NEET JTC算法能给出目标扩展状态更精确的轮廓信息。

理想情况下，若计算得到目标属于某类别概率接近于1，就能准确地判断出该目标的类别标签。当类别为1、2和3的目标分别存在于监视区域时，NEET JTC算法计算其属于类别1、2和3的概率约等于1，这与实际情况相符，如图6(a)、图7(a)和图8(a)所示。而在相同仿真场景下，JTC-RMM算法计算得到的目标概率约为0.5、0和0.4，说明JTC-RMM算法对类别的判断出现错误，如图6(b)、图7(b)和图8(b)所示。仿真结果表明，NEET JTC算法能克服JTC-RMM算法的缺点，能对尺寸相似但形状不同的目标进行准确的分类。

(a) NEET JTC类别概率(a) Class probability obtained by NEET JTC

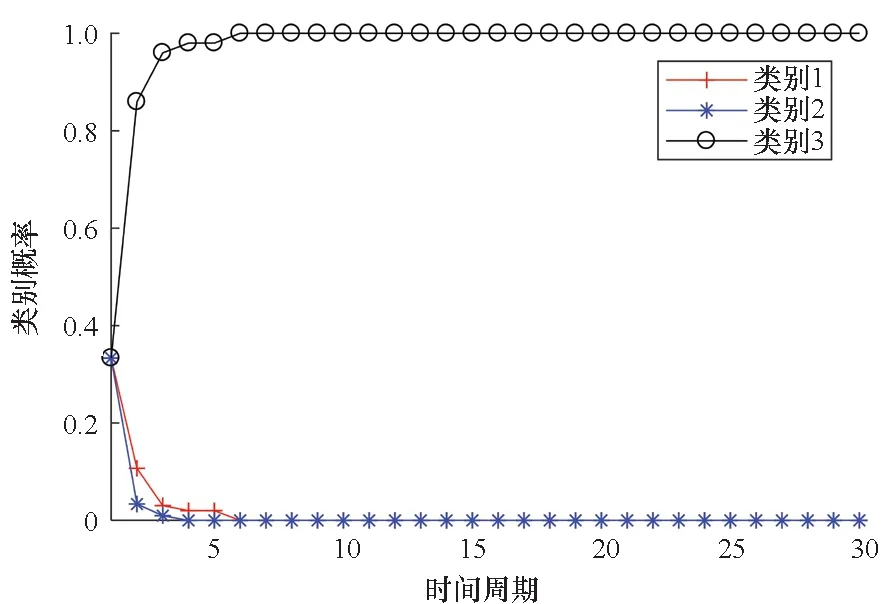
(a) NEET JTC类别概率(a) Class probability obtained by NEET JTC

4.2.2 场景2实验结果

利用NEET JTC、ETT-PF和ETT-UKF三种算法对目标状态估计的单次运行结果如图9所示。

(a) 类别1(a) Class 1

由图9可知，对于初始时刻的目标状态估计，ETT-PF和ETT-UKF算法得到的目标形状近似为椭圆，而NEET JTC算法则能给出目标形状(轮廓)的准确描述。在目标保持匀速直线运动的条件下，ETT-PF和ETT-UKF算法对目标形状的估计结果逐渐与NEET JTC算法的估计结果一致，但NEET JTC算法的运动学状态估计性能优于ETT-PF和ETT-UKF算法。当目标发生机动之后，NEET JTC算法仍能保持良好的运动学状态和扩展状态估计，此时ETT-PF和ETT-UKF算法对目标运动学状态估计出现较大偏差，形状估计质量也严重下降。

在场景中分别出现类别为1、2和3的目标仿真条件下，开展100次蒙特卡洛实验，所得目标的状态估计和分类结果如图10、图11和图12所示。

(a) 位置RMSE(a) RMSE of position

由图10～12中的结果可以看出：①目标未发生机动时，ETT-UKF和NEET JTC对运动学状态估计性能几乎一致；随着几个时间周期的积累，ETT-UKF具有和NEET JTC算法相近的扩展状态估计性能；相比之下，ETT-PF对目标的状态估计性能是三者之中最差的。②当目标发生机动时，ETT-UKF对运动学状态和扩展状态的估计性能急剧下降，ETT-PF算法对目标形状估计的性能略优于ETT-UKF算法，而NEET JTC算法几乎不受目标机动的影响。在整个监视时间范围内，NEET JTC算法对目标状态估计性能基本维持不变，说明算法具有强鲁棒性，如图10(a)～(b)、图11(a)～(b)和图12(a)～(b)所示。③此外，无论目标机动与否，NEET JTC算法都能对目标进行准确分类，如图10(c)、图11(c)和图12(c)所示。仿真结果说明，本文所提算法对估计目标状态和判断目标类别是完全有效的，同时也说明采用目标联合跟踪与分类处理技术能提高目标状态估计的精度。

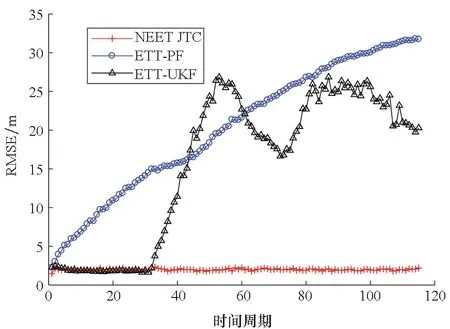
(a) 位置RMSE(a) RMSE of position

4.2.3 算法复杂度

通过评估NEET JTC、ETT-PF和ETT-UKF算法的运行时间，来分析对比三种算法的复杂度。仿真实验是在MATLAB2018a上进行的，计算机的基本配置是3.60 GHz Intel(R) Core(TM) i7-7700和16 GB RAM。

对场景2进行100次蒙特卡洛实验，得到NEET JTC、ETT-PF和ETT-UKF算法在每个采样处理周期中的平均时间开销如表1所示。由此可以看出，ETT-PF算法运行时间最长，这是因为该算法中状态维度高，需要大量的粒子来保证目标状态估计的精度；ETT-UKF算法由于处理过程简单，执行速度最快；相比之下，NEET JTC算法因在对目标类别的求解过程中采用了粒子实现形式，算法运行时间略高于ETT-UKF算法，但其仍具有良好的实时处理性能。

表1 三种算法运行时间

5 结论

本文提出了一种非椭圆扩展目标JTC算法——NEET JTC，该算法基于星凸RHM，将目标状态分解为两个矢量，并通过目标类别先验信息与目标瞬时扩展状态的关系，将目标类别先验信息集成到统一的滤波理论框架中。为了解决目标观测方程高度非线性导致的无法解析求解目标类别更新算式的问题，文中利用粒子采样技术，获得数值近似最优解。仿真结果表明，所提算法能克服传统基于RMM的JTC算法缺点，可对尺寸相近、形状不同的目标进行准确分类；与标准的基于星凸RHM的扩展目标跟踪算法相比，所提算法能同时改善目标运动学状态和扩展状态的估计效果，且在目标机动时仍具有稳定的估计性能；此外，所提算法复杂度适中，具有良好的实时性。