基于Adams和MATLAB的赛车转向系统联合仿真优化

刘仕康，周坤，樊昕宇

（燕山大学，河北 秦皇岛 066000）

0 引言

大学生方程式赛车最早起源于上世纪的美国。中国大学生方程式汽车大赛（简称“中国FSC”）是一项由全国高校车辆工程或汽车相关学科在校学生组队参加的赛车设计与制造比赛。2010年第一次举办大学生方程式比赛,参数队伍近20队，2022年增加到了近100队。大赛车队要求在一年时间内制造一辆符合赛事规则和制造标准小型单座方程式赛车并参加静态答辩和动态测试形式，以总分高低决定胜负[2]。转向系统关系到赛车的操纵稳定性，对整车性能起着重要的作用，通过对转向系统的优化，有利于改善转向操纵稳定性和轻便性。本研究提出了用Adams/insight模块和Matlab联合仿真的思想，对转向阿克曼系数和轮跳时前束角的变化进行优化，使实际阿克曼系数曲线与理想阿克曼系数曲线拟合程度越好的同时，轮跳时前束角的变化也在可接受的范围内。

1 FSEC转向数学模型[3]

断开式转向梯形分为：梯形、转向器前置，梯形前置、转向器后置，梯形后置、转向器前置，梯形后置、转向器后置4种形式。受限于赛车内部狭小空间的布置，为了转向时防止横拉杆与制动、双横臂悬架、轮辋产生干涉。我们采用的是断开式梯性前置、转向器前置的布置方式，根据赛车内部实际的转向结构，建立实际的内外轮转角关系，如图1所示。

图1 转向梯性整体结构图

为了清楚地表达动态转向时的内外轮的转角关系。绘制当车轮向左转动时，左右车轮运动简图，如图2所示。

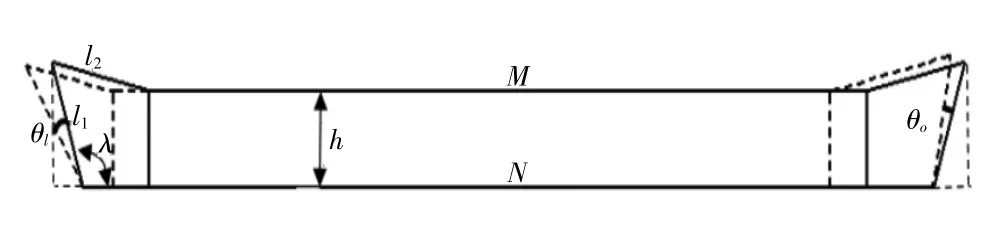
图2 转向轮实际转角关系示意图

车轮左转，外轮转向角度为θo，根据几何关系可知：

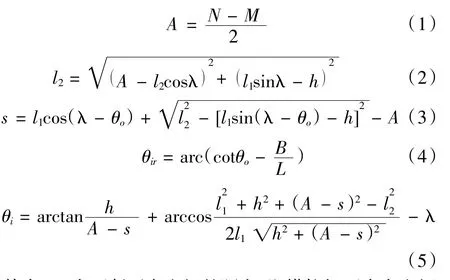
其中：M为两断开点之间的距离，即横拉杆两内点之间的距离，mm；N为两侧车轮主销延长线在地面上交点之间的距离，mm；h为前置转向器与前轴之间的距离，该距离用于定位转向器位置，也是所谓的梯性高，mm；L为梯性臂的长度，mm；λ为梯性底角；A为计算算子；l2为拉杆长度，mm；s为齿条行程，mm；θi为内轮转角；θir为符合标准阿克曼关系的内轮转角；θo为实际外轮转角。

从公式中可以看出，由梯性参数所构成的内外轮转角极度非线性，且包含的优化变量众多，使用常用的优化函数无法达到很好的优化结果，因此考虑利用Adams/insight工具来进行优化，并用Matlab检验的方式来实现联合优化的效果。

2 Adams多目标优化

2.1 建立Adams转向悬架模型

初步确定转向几何后，用Adams/Car建立转向悬架虚拟样机模型如图3所示。进行平行轮跳仿真。为后面导入Adams/Insight模块作准备。

图3 悬架转向虚拟样机模型

用Matlab编写程序得到实际阿克曼系数（阿克曼系数就是考虑轮胎侧偏时的内外轮转角差与不考虑轮胎侧偏时的内外轮转角差的比值）和加入侧偏角时阿克曼系数的差值。阿克曼系数的意义在于修正侧偏情况下的内外轮转角关系，如图4、图5所示。当得到较好的阿克曼系数状态下的轮跳时束角的变化却不是很理想，如果对阿克曼系数单一变量进行优化时得到的悬架转向模型工况轮跳时前束角的变化就不是很理想。如果只对前束角进行优化，不考虑阿克曼系数的变化，则利用Adams/insight模块对前束角优化，不断迭代使前束角变化到最小，此时阿克曼系数就会变的不理想。因此能对轮跳时前束角的变化和阿克曼系数同时优化是最好的选择。

图4 优化前阿克曼系数随内外轮转角变化图

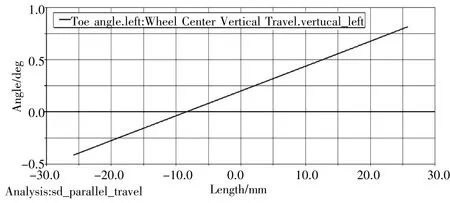
图5 优化前前束角随轮胎跳动变化图

2.2 基于Adams/Insight模块对阿克曼系数和前束角进行多目标优化

通过Adams/Insight模块对转向梯形进行多目标优化，可以同时优化阿克曼系数与前束角的变化，避免出现优化单一变量而另一个变量出现变差的情况。

（1）点击Design objective命令寻找目标值，目标值选取为“仿真中的最大绝对值”。

（2）点击adams/insight命令进入adams/insight模块，找到要优化的点，调节其想要的运动范围并命名。

（3）最后求解，等其运算结束后，显示其结果，输入实验名称进入结果页面。

（4）根据自己预想的优化结果赋予两个优化目标合适的比重（对于特定路况行驶的车辆，例如FSEC，转向工况较多，应多考虑阿克曼系数，因为匹配的阿克曼转向可以使得四轮尽可能地做纯滚动从而减少轮胎的磨损，如果直线路况较多，应多考虑轮跳时前束角的变化，因为轮跳时前束角变化过大会影响车辆的直行稳定性，不足转向和过度转向，权重的值根据车辆的目标路况来确定，然后得到优化后的结果。考虑到我们有更多的转向工况，这里选取阿克曼系数的权重为0.7、前束角的变化为0.3，如图6所示。

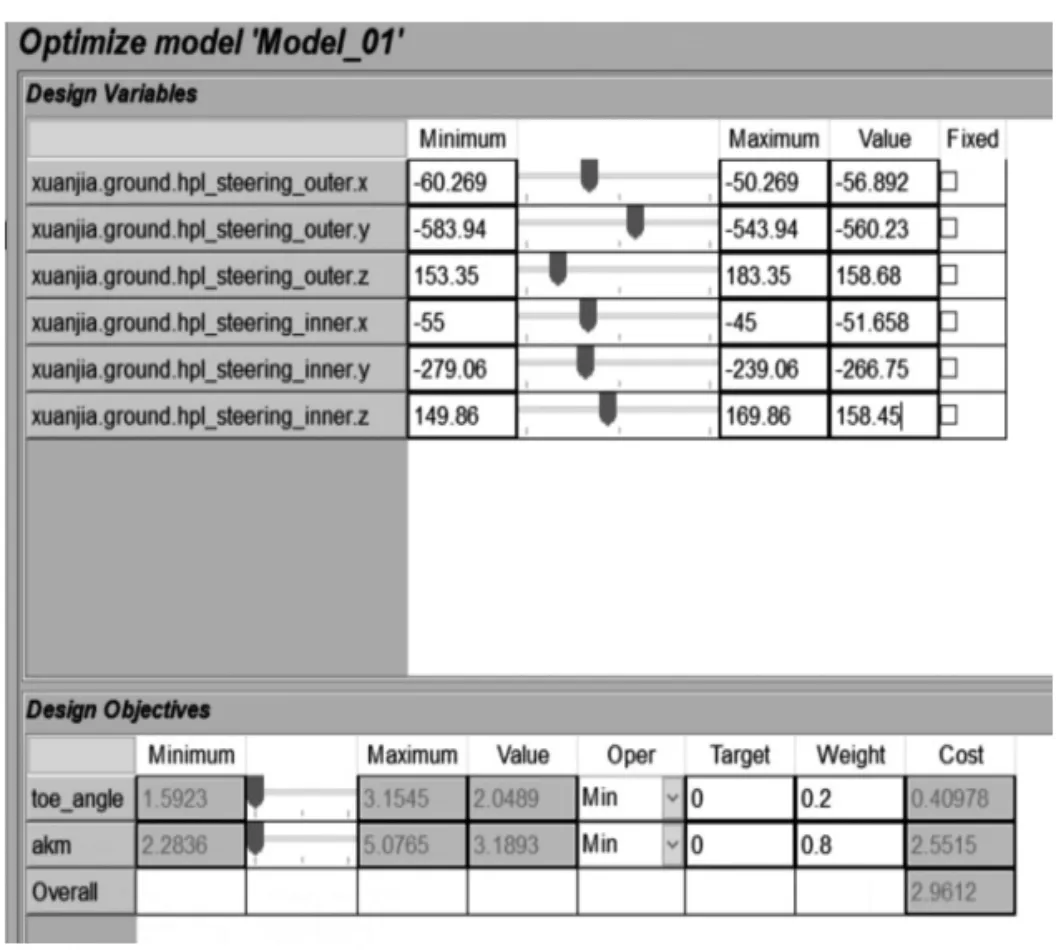
图6 优化结果图

（5）得到优化后的硬点坐标后，将其转化为对应的梯性参数，见表1。由表1可知，梯形底角明显变小，节臂长和梯形高没有明显变化，由此得出，转向梯形中梯形底角对转向性能有较大影响。

表1 梯形参数

3 Matlab对优化结果的验证

3.1 标准阿克曼转向关系[4]

转向不考虑侧偏角的影响，如图7所示。为了让赛车转向时的各个车轮都只做纯滚动运动，一方面可以提高赛车在过弯时的操纵稳定性能；另一方面可以减小因滑动而带来的轮胎不均匀的磨损。此时，转向中心应位于赛车后轴线的延长线上，此时内外轮转角应符合标准阿克曼转角关系：

式中，θo为外轮转角；θi为内轮转角；B为主销后倾角为0°时，两侧车轮主销与地面交点之间的距离，mm；L为轴距，mm。

由（6）式得，在给定的外轮转角下，内轮转角为：

3.2 考虑侧偏角时的左右轮转角关系[3]

标准阿克曼转向关系没有考虑在实际工况下由于高速过弯时存在的侧偏角，这会导致转向中心并不位于后轴延长线，而是距后轴有一距离m，如图7所示。

图7 考虑侧偏角时左右轮转角关系

为了便于推导，在考虑侧偏角时转向左右轮关系式，以转向中心为原点，汽车前进方向为X轴正方向，垂直X轴指向上方为Y轴正方向，建立坐标系。设转弯半径为R，转向中心偏离后轴距离为m，轴距为L，轮距为B，则各点坐标如图7所示。

根据三角函数关系，推出算式：

式中：θi为理想内轮转角；θo为理想外轮转角；σf为前轴中点侧偏角；σr为后轴中点侧偏角；C=B/2L。

式（8）即为考虑了侧偏角对转向轮影响的理想内外轮转角关系式。如果给出轮胎侧偏角，就能够根据下文的式（11）计算出考虑轮胎侧偏角时的内外轮转角关系。

3.3 确定阿克曼系数

在前文中，通过设置阿克曼权重来决定硬点优化时阿克曼对硬点优化时的影响程度，而为了验证硬点优化的合理性，则我们必须通过其他的手段来确定一个合理的阿克曼系数。

（1）定义阿克曼校正系数[4]

其中：θi为实际内轮转角；θo为实际外轮转角；θit为当外轮转角θo为满足标准阿克曼公式的内轮转角。根据定义可知，当K=1时，即为标准阿克曼转向；当K=0时，实际内外轮转角相同，为平行转向；当K＜0时，外轮转角角度大于内轮转角角度，为反阿克曼情况。阿克曼校正系数可以很好的描述转向关系由标准阿克曼关系向平行转向过度的程度。当定义了阿克曼校正系数之后，目标转向关系的优化设计其实就是阿克曼校正系数的优化。

通过阿克曼校正系数可以定量化地描述转向梯性的关系特性。因此，我们可以将目标转向关系—即合理的内外轮转角关系转变成阿克曼校正系数的优化。

（2）建立目标转向关系优化函数[4]

将（9）代入（7）中可得：

根据（8）可得

合理的目标转向关系，即合理的阿克曼校正系数应该保证θi1与θi2尽可能地接近，两曲线应尽可能吻合。

引入加权因子ω构成目标转向关系优化函数如下

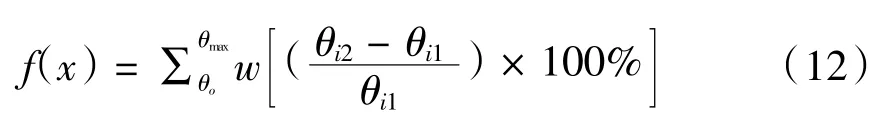
其中：w表示赛车行驶过程中方向盘各角度使用频率。

方向盘上的转角记录仪器记录了耐久赛过程方向盘转角数据，通过对不同角度使用频率进行分析可知，10°以下的转角使用较为频繁，10°～20°的转角次之，20°以上转角频率最低，确定加权因子如下：w=1.5（0＜θo＜10°）

K值的优化范围为0≤K≤1，根据最小转弯半径确定θmax=27.627°。

利用Matlab编写优化程序，运行得到优化结果如图8所示。从曲线图中可以看出，随着阿克曼校正系数的增大，误差也就是理想和实际的车轮转角差值出现先减小后增大的变化，当我们取误差值最小时，也就是实际与理论差距最小，就得到了我们想要的阿克曼校正系数，为45%，此时实际与理想最小意味着转弯时做纯滚动的能力是在所有阿克曼校正系数中最强的，这正是我们想要的。

图8 阿克曼优化曲线

在优化时要注意考虑轮胎侧偏角对转向关系的影响的基础上，这里根据赛事的典型工况——“八”型绕环的极限工况下的载荷转移来考察所赋予的合适的前后轮侧偏角，最后得到最佳阿克曼校正系数为45%，并得到目标转向关系为：

3.4 对优化结果验证

通过前面推出的带阿克曼校正系数的目标转向关系和前文提到的实际机构的内外轮转角关系，当两者的曲线靠的足够近，或者相对优化前有了较大的提升，就说明了优化的正确性。优化结果对比如图9、图10所示。

图9 优化前后转角差对比

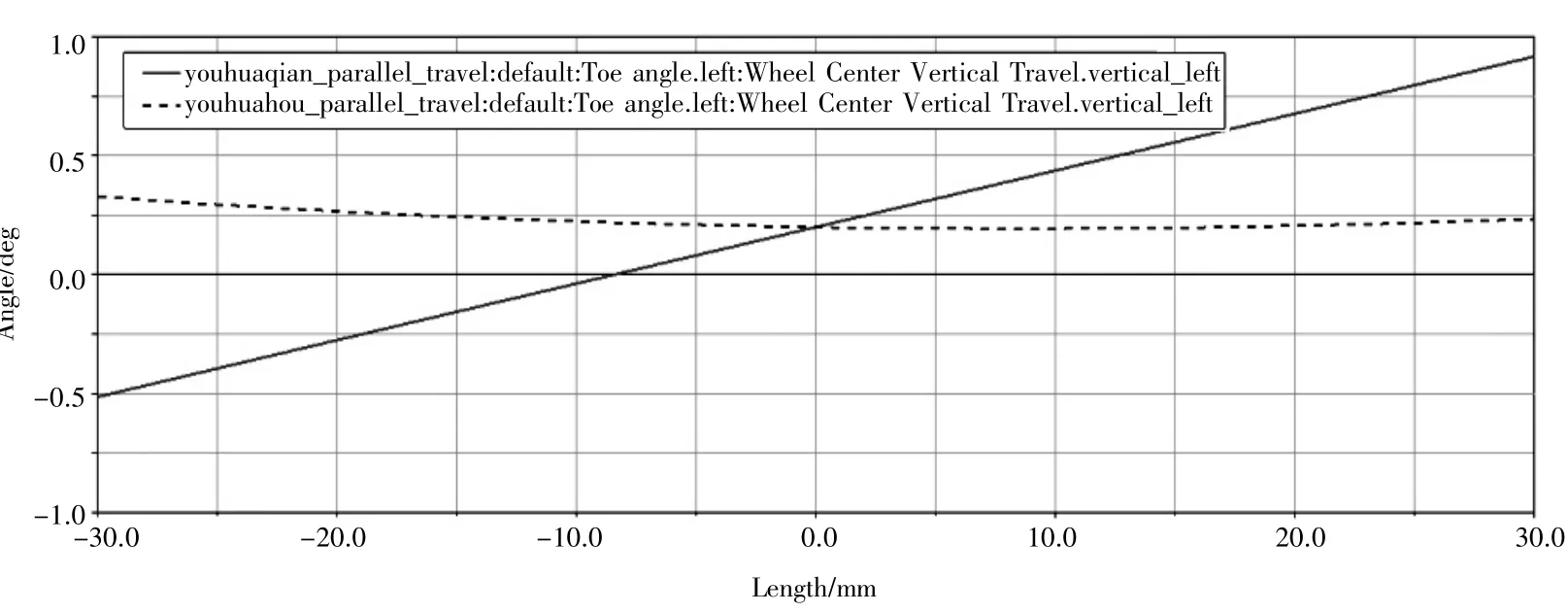
图10 优化前后前束角随轮胎跳动变化图

结果表明，轮跳时前束角的变化明显减少，使轮跳时前束角的变化由1.5°降低为0.25°，降低了83%，最大转角差值由1.291°减小为0.7548°，降低了41.53%。优化效果显著，证明了本方法的有效性。

4 结语

以中国大学生方程式为背景，提出了一种基于Adams/car insight模块以轮跳时前束角的变化以及阿克曼系数为优化目标对转向系统节臂点和断开点的优化方法。详细分析了转向硬点的优化步骤，文中提及的优化方法相对于一般的优化方法更具简便性和实用性，大大减少了设计周期，对FSEC转向系统的优化具有一定的参考作用。