水下蒸汽涡轮发动机的动态建模与控制研究

吴亚军，刘洋

（1.海军装备部，陕西 西安 710000；2.中国船舶集团有限公司第705研究所，陕西 西安 710075）

0 引言

无人水下航行器（Unmanned Underwater Vehicle，UUV）在捍卫国家安全、开发海洋资源等领域有着至关重要的作用，一直是各国的研究热点。动力源作为其技术发展的主要瓶颈，直接影响水下航行器的性能[1]。受限于当前材料、设计和工艺水平等因素，传统的水下航行器用活塞式发动机很难进一步提高功率。而现有电池的比能量又无法满足水下航行器长时间续航的要求。以蒸汽涡轮发动机为主机的水下闭式循环系统具有高比能量、大比功率和无工质排放等优点[2]，被视为高性能水下航行器动力源的未来发展方向之一。

采用蒸汽涡轮发动机作为无人水下航行器闭式热力循环系统的主机，其经济性也优于活塞式发动机[3]。如美国的MK50型鱼雷即采用蒸汽涡轮发动机作为其Li/SF6闭式循环系统的主机，其最大航速超过50 kn，最大航深可达1000 m[4]。Li/SF6闭式循环系统如图1所示。金属Li和SF6在热管反应器中发生反应，产生大量热量。热管反应器外壁被蒸发器包覆，其中的液态水吸热变成蒸汽进入涡轮机，带动涡轮机轴旋转。做功后的乏汽经冷凝器冷却后，变为液态水，由泵输送进入下一个循环。

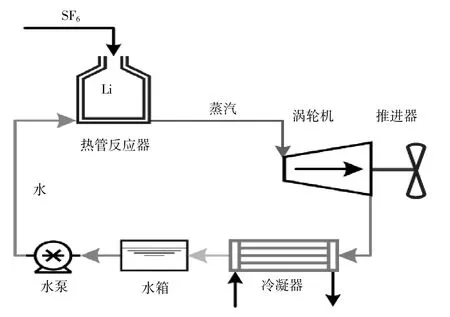
图1 Li/SF6闭式循环系统

在实际工程中，转速作为蒸汽涡轮机的控制目标，主要与进入发动机的蒸汽流量有关。涡轮机入口蒸汽流量可通过闭式循环系统中的水泵精准调控。随着进入喷嘴的蒸汽流量增多，喷嘴室的压力升高，进而流入汽缸的蒸汽流量增加，蒸汽涡轮发动机功率增大，转轴转速相应升高。因此，蒸汽涡轮机控制系统的控制量为入口蒸汽流量。在现有的研究中，涡轮机的转速控制主要采用PID反馈控制[5-6]，且各参数多为试凑法得出。利用试凑法求解PID参数，工作量大且易造成系统超调，严重影响系统性能。

针对以上问题，通过分析蒸汽涡轮发动机的动态过程明确了其关键动态环节，采用小偏差线性化的方法建立了其线性模型，在此基础上进行PID控制，提出了一种基于遗传算法的PID参数优化策略，并进行了仿真验证。

1 涡轮机建模

建立蒸汽涡轮发动机的动态模型是设计控制系统的前提。然而蒸汽涡轮发动机中存在复杂的热力、流体和机械效应耦合，因而其动态特性在本质上是非线性的。这些非线性特征将随初始条件和当前工况的变化而变化，导致采用非线性模型设计的控制系统难以保证控制效果，因此在工程实践中仍需建立线性模型，并用线性控制设计技术进行控制器设计[7]。

从动态角度分析可知，蒸汽涡轮发动机的工作过程中有两个动态环节，一个是喷嘴，另一个是转轴，因此可以将蒸汽涡轮发动机简化为由蒸汽容积模块和转子模块构成的物理模型，如图2所示。

图2 蒸汽涡轮发动机的简化物理模型

1.1 蒸汽容积模块

由气体流动的连续性方程可知

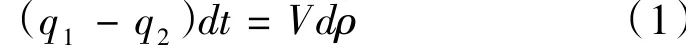
由流量特性可知蒸汽容积的出口流量与其压力成正比，即q2=kp，代入式（1）得

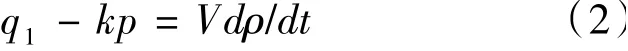
假设气体的状态变化是按多变过程进行的，即p/ρn=常数，则该式两边取对数并求导得：

将式（3）代入式（2）得

因为p，ρ均是时变的，所以式（4）本质上是非线性的。采用小偏差线性化的方法将其转化在工作点附近转化为线性方程。设p0，ρ0，q0均为额定工况下所对应的参数，则每一个变量都可以写成额定值加变化量的形式，即p=p0+△p；ρ=ρ0+△ρ；q1=q10+△q，将以上各式代入式（4）得：

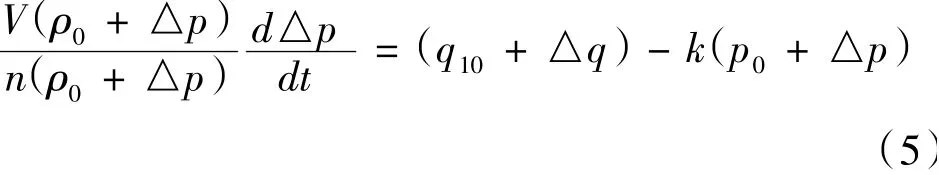
因为在额定工况下出入口流量均等于额定流量，即qm0=q10=q20，且q20=kq0，将以上两式代入式（5）得

因为△p，△ρ与p0，ρ0相比是一个微小的变化量，因而可以将V（ρ0+△ρ）/n（p0+△p）近似为Vρ0/nqm0。实践表明，这种小偏差线性化所带来的误差仅为1%～2%。所以式（6）可以简化为

将式（7）两边同时除以额定流量qm0，得

上式中的各变量习惯上用额定值的百分比表示，即△q/qm0=xq，△p/p0=xp，则式（8）可写成

将式（9）两边进行拉氏变换可得

式中，T0=Vρ0/nqm0称为容积时间常数，用以描述容积惯性，即以额定流量qm0向蒸汽容积中注入体积为V的蒸汽时，使蒸汽容积中的蒸汽质量从零增加到D0=Vρ0所需要的时间。

1.2 转子模块

转子的力矩平衡方程为：

式中，J为转子的转动惯量，ω是转子的角速度，TT是蒸汽转矩，TL是负载的反转矩，Tf是摩擦转矩。

相应的转子功率平衡方程为：

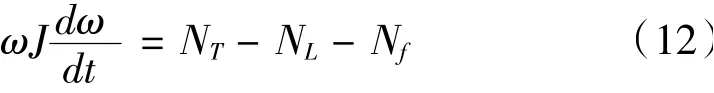
式中，Nf是一个与ω有关的非线性函数，NL是一个外部变量。

对式（12）进行小偏差线性化，可得

因为额定工况下NT0-NL0-Nf0=0，并将（ω0+△ω）J△ω/dt近似为ω0J△ω/dt，式（13）可化为

式（14）两边同时除以额定功率NT0，可得

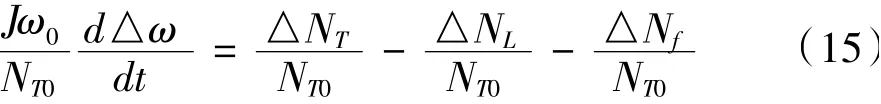
上式中的各变量用额定值的百分比表示，即△ω/ω0=xn，△NL/N0=xNL，△NT/N0=xP。此外在工作点附近△Nf可以表示为

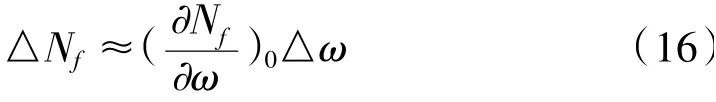
将以上各式代入式（15）可得

式（17）可以简化为

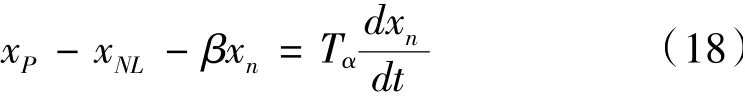
将式（18）两边进行拉氏变换，得

式中，Tα称为转子飞升时间常数，用以描述转动惯性，表示转子在额定功率的蒸汽主力矩作用下，转速由零飞升到额定转速所需的时间。β称为自平衡系数，与附加损耗有关。

最后，将蒸汽容积模块和转子模块联结起来，得到蒸汽涡轮发动机入口蒸汽流量与输出转速的关系框图，如图3所示。

图3 蒸汽涡轮发动机的传递函数框图

2 基于遗传算法的PID参数优化

PID控制由于具有算法简单、鲁棒性好、可靠性高等优点而被广泛应用于系统控制领域。其典型传递函数为：

PID控制器参数kp，ki，kd调整是否恰当，将直接决定此控制器的控制效果。PID参数整定一般采用手工试凑或优化的方式。前者工作量大且效果不理想。PID参数优化则通过数学方法对kp，ki，kd进行优选，从而使目标函数达到极值，因而本质上是一个参数寻优问题。采用优化方法整定PID参数工作量小，且精度高，控制效果好。因此，通过构造基于性能指标加权的目标函数，采用遗传法对PID参数进行优化。

为获得良好的动态特性并减小控制输入的波动，PID参数优化的最小目标函数选为：

式中，e（t）为系统误差，u（t）为控制器输出，tu为上升时间，w1，w2，w3为权值。

此外，可添加超调惩罚项以避免超调，此时目标函数为

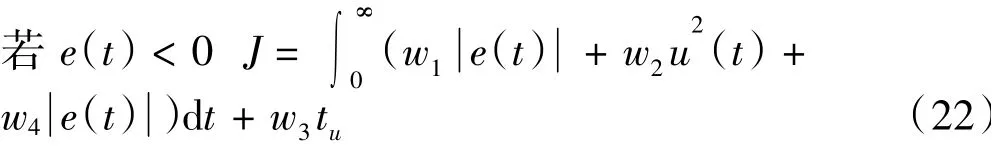
式中，w4为权值，且w4≫w1。

遗传算法是一种基于生物遗传和进化机制的寻优搜索算法，因其具全局优化能力且收敛迅速，已广泛应用于函数优化等方面。其基本思想是根据问题的目标函数构造一个适应度函数，对由多个解（每个解对应一个染色体）构成的种群进行适应度评估和遗传运算（包括复制、交叉和变异），经多代繁殖后最终获得适应度值最好的个体作为问题的最优解[8]。应用遗传算法优化PID参数的基本流程如下：

（1）把每个PID参数按照一定编码方案进行编码得到字串，再将这些字串联成一个完整的染色体，即个体；

（2）随机产生由N个个体构成的初始种群；

（3）将种群中各个体解码成对应的参数值，用此参数求目标函数值；

（4）计算适应度函数；

（5）应用复制、交叉和变异算子对种群中的个体进行操作，形成新一代的种群；

（6）反复执行步骤（3）～（5），直至满足收敛判据为止，解码后输出PID参数值J。

优化流程图如图4所示。

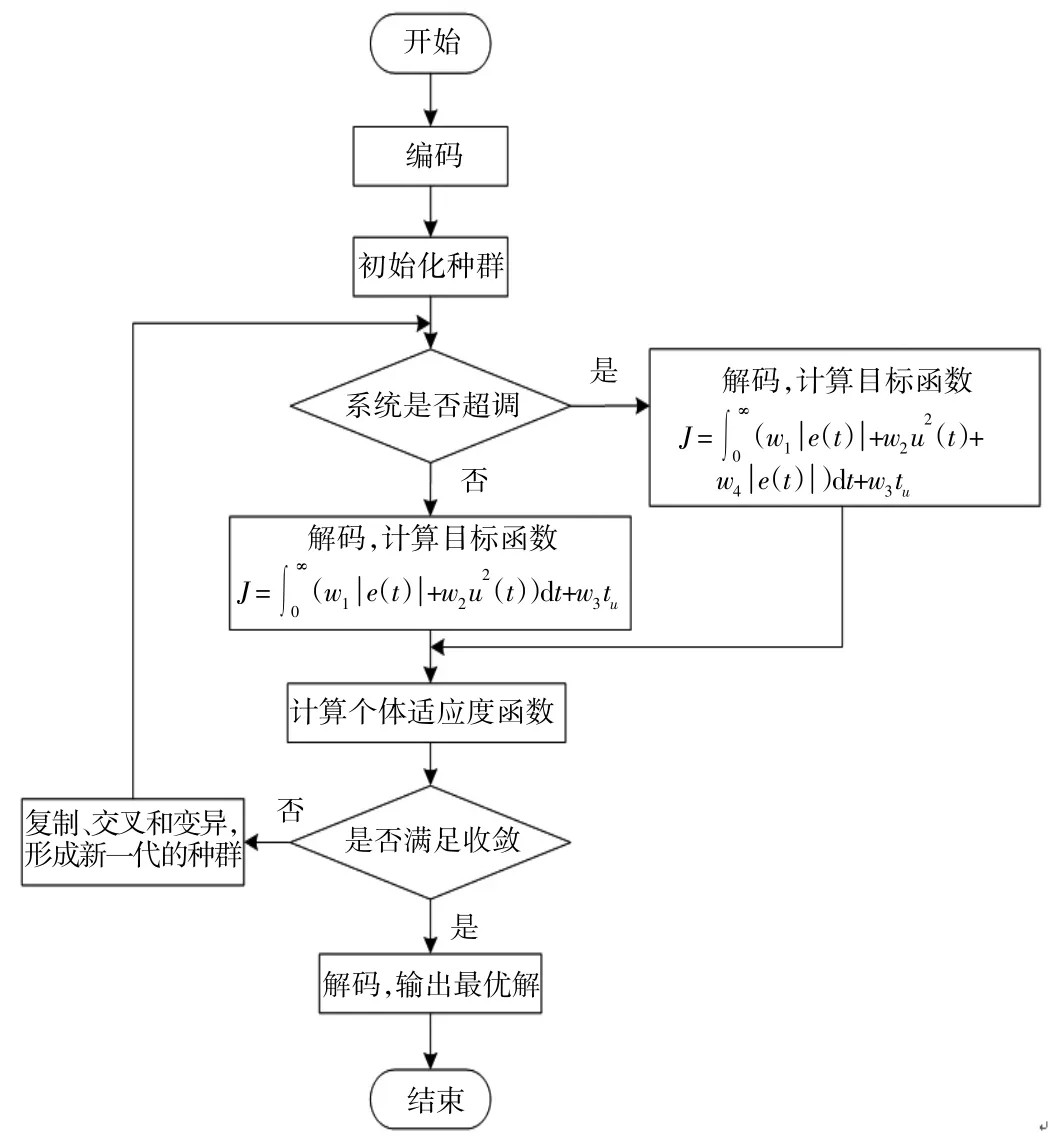
图4 遗传算法优化PID参数流程图

3 仿真实验

为验证该PID参数优化方法，以所建立的蒸汽涡轮发动机模型为控制对象进行仿真研究。假设蒸汽涡轮发动机的负载为零，其他参数分别为：Tα=0.16，T0=1，β=0.83，则其传递函数为：

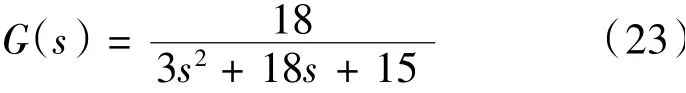
遗传算法采用实数编码方式，其参数选择见表1。

表1 遗传算法参数

经过100代进化，获得的优化结果如下：kp=4.7929，ki=2.5064，kd=1.4187，性能指标J=99.6934。性能指标的优化过程如图5所示。由图可知，采用遗传算法收敛至最小值实际只需约30步的迭代计算，证明该算法收敛速度快，优化效率高，是一种适用于工程应用的参数寻优方法。

图5 性能指标J的变化曲线

采用整定后的PID控制系统阶跃响应如图6、图7所示，其中图6为转速变化曲线，图7为入口蒸汽流量变化曲线。图中数据均做了无量纲化处理，它们是实际值与额定值的比值。可以看出，经过参数优化的PID控制器响应快速、无超调，控制效果良好。

图6 小波包前面板

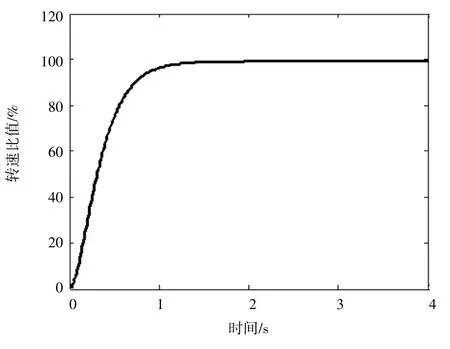
图6 蒸汽涡轮发动机的转速变化曲线

图7 蒸汽涡轮发动机的入口蒸汽流量变化曲线

4 结语

通过分析蒸汽涡轮发动机的动态过程明确了其关键动态环节，采用小偏差线性化的方法建立了其线性模型，并在此基础上进行PID控制，提出了一种基于遗传算法的PID参数优化方法。仿真实验证明遗传算法收敛速度快，优化效率高，是一种适用于工程应用的参数寻优方法，经过参数优化后的PID控制器响应快速、无超调，控制效果良好。