太阳辐射对航空发动机露天试车台热变形的影响

汪 才，艾延廷，张 巍，林 山，汪 英

(1.沈阳航空航天大学，沈阳 110136；2.中国航发沈阳发动机研究所，沈阳 110015)

1 引言

航空发动机研制过程中，需要在露天环境下完成大量的环境试验，如吞咽试验、吞鸟试验、吞沙试验、吞水试验等，为此露天试车台是航空发动机整机试验配套系统中不可缺少的组成部分。与室内试车台相比，露天试车台属大跨度钢结构，且暴露在室外各种环境中，因此其必然会受到气候、声波等许多外界因素的影响，如太阳辐射(温度及温度分布不均)、风吹(风力机风向)、雨淋、噪声等因素影响，而这些因素对露天试车台结构性能及其试验测试精度有直接影响。

近年来，国内外学者对露天环境下大跨度钢结构特性分析方法进行了系统的研究，也在先前研究的基础上，探索出了一些全新的分析方法与技术手段。如沈世钊进行了大跨度刚结构的理论研究，并在工程实践中进行了广泛应用；刘锡良在现代空间结构中对大跨度钢结构进行了系统阐述。随着试验技术的进步，分析环境对结构产生影响逐渐成为学者研究的热点。如金晓飞等提出了大跨度空间钢结构在露天日照作用下的热分析方法；王元清等研究了露天日照条件下钢结构构件温度的变化；Kim等对钢箱形梁桥受太阳辐射影响产生的形变规律进行了探究；Kondrachuk 等对刚性构件吸收太阳辐射能力进行了探究，并分析了热力学在工程史上发展的状况；Alinia等对双层网钢架结构进行了热负荷的模拟及探究；Hamed 等对球顶大跨度钢结构进行了热力学瞬态响应试验与分析；陈建稳等研究了日照条件下空间钢结构的温度效应。大批学者亦对太阳辐射量的计算方法进行了较为深入的研究。如张鹤飞总结了与太阳辐射量有关角度的定义和计算公式；陈晓勇等考虑了建筑日照计算中，对太阳赤尾角公式的应用方法；李锦萍等根据ASHRAE 模型对北京晴天太阳辐射模型进行了深入研究；白心爱总结了辐射换热角系数的计算方法；刘艳峰等对结构壁面换热系数进行了分析与整理。综合国内外研究现状，针对露天环境下大跨度钢结构受太阳辐射影响研究的深度仍有待提高。

太阳辐射是对露天试车台架结构性能影响最为复杂的因素，如季节、太阳位置的改变，会引起太阳辐射角度和强度的变化，且其变化过程复杂，存在着许多不确定性因素，导致太阳辐射所引起的温度场呈非均匀变化。目前，考虑太阳辐射引起温度场变化的计算方法大多未经过验证，很多计算前的参数取值也没有可靠的依据。在常规的结构设计中，没有针对日照温度效应影响的专门计算方法，有些特殊结构需借助专门的计算方法计算，但计算精度无法保证。因此，针对整体大跨度钢结构在太阳辐射作用下的温度场及应力场分布规律的研究，对结构的前期设计与安全使用都有着深远的意义。本文使用ASHRAE 模型计算太阳辐射强度方法，对ANSYS Workbench 仿真计算结果进行对比校正，通过模拟太阳辐射，来计算航空发动机露天试车台产生的热变形，以期为航空发动机露天试车台的校准与使用提供参考。

2 太阳辐射强度计算

2.1 计算方法

利用ANSYS Workbench中Fluent软件的太阳辐射功能，实现太阳辐射模拟，使用Fluent 软件中的Solar Calculator功能模块，计算太阳辐射强度。使用ASHRAE模型计算的露天试车台地域太阳辐射强度作为对比，验证使用Solar Calculator 功能模块计算太阳辐射强度的准确性。

要确定辐射源的方位和角度，需要获取计算地点的地理纬度、太阳时角Ω、太阳赤纬角、日角、元旦开始的日系数(即一年中的第几天，范围是1～365 天)，计算太阳高度角和太阳方位角。以上各个角度定义如图1和图2所示。

图1 地理纬度、太阳时角和太阳赤纬角图Fig.1 Geographic latitude,solar time angle and solar declination angle map

图2 太阳高度角和太阳方位角Fig.2 Solar altitude angle and solar azimuth angle

太阳高度角和太阳方位角可用下列公式计算：

式中：为24 h制计算时刻；为积日，即日期在本年的序号，如1 月1 日积日为1，平年、闰年的12 月31日积日分别为365 和366；为年，如2019 年，就是2019。

有了上述公式计算所得的参数，就可根据下列公式计算太阳的辐射强度：

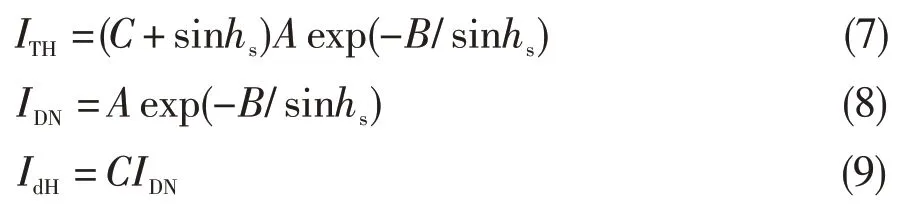
式中：为水平总辐射强度；为太阳直接辐射强度；为水平散射辐射强度；为大气质量为0 时法平面上得到的太阳直射辐射强度；为大气消光系数；为散射辐射与垂直入射辐射的比值。其中、、的取值如表1所示。

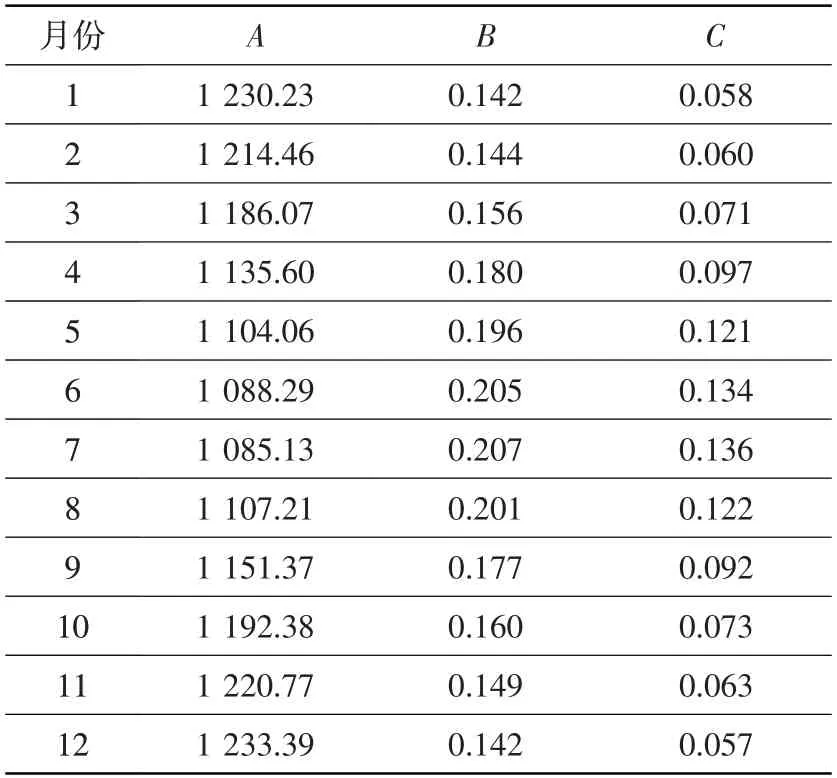
表1 ASHRAE参数取值表Table 1 Table of ASHRAE parameter values

2.2 露天试车台简化模型

露天试车台整体结构复杂、零部件较多，其中管、孔、防护网等结构，极大地增加了计算的难度，且考虑到这些结构对计算结果的影响极小、可以忽略，故对露天试车台整体结构进行简化。简化后的具体模型如图3所示。

图3 航空发动机露天试车台简化模型Fig.3 Aero-engine open-air test bench model diagram

2.3 计算模型边界条件

计算模型的边界条件为：模型Wall边界条件均设置为固定、无滑移，温度选项中选温度项，其中外部温度选择为当时气温(与Solar Calculator中所选择的月份及具体时间相匹配的温度)，辐射选项中设置为不透明。利用Fluent 求解时，各参数的离散采用二阶精度格式。解收敛标准为相对残差小于10，残差不再明显减小且Energy不随时间变化。

3 太阳照射对露天试车台变形的影响

3.1 太阳辐射强度的计算验证

以3 月21 日太阳辐射强度计算证明算例，验证太阳辐射强度计算结果正确性。利用公式(1)～(6)，其中3 月21 日经过计算=-0.273 7°，=-0.088 21°，选择时间为12 点，Ω=0°，sinh=0.738 6，cos=1，利用公式(7)～(9)可计算出=960.245 0。由于计算太阳辐射强度时采用的公式、方法存在不同，所忽略的实际情况也各不相同，故存在不同程度的误差。用公式(10)分别计算选定的4天误差率，结果见表2。

表2 Solar Calculator功能模块与ASHRAE模型计算的太阳辐射强度对比Table 2 Comparison of solar radiation intensity calculated by Solar Calculator functional module and ASHRAE model

式中：为用Fluent 中的Solar Calculator 功能模块计算出的太阳辐射强度，为用ASHRAE 模型计算出的太阳辐射强度。

根据表2中数据可知，不同时间采样点下，利用Solar Calculator 功能模块与ASHRAE 模型计算的太阳辐射强度间的误差低于5.20%。据此，可认为Solar Calculator功能模块的计算结果准确可用。

3.2 太阳辐射对露天试车台温度影响分布

以6月21日13时为例，计算露天试车台经太阳辐射所产生的温度分布变化。假定为晴朗天气，则Solar Calculator功能模块计算结果如图4所示。

图4 6月21日13时Solar Calculator功能模块计算结果Fig.4 Calculation results of Solar Calculator function module at 13∶00 on June 21

参考斯特藩-玻尔兹曼定律，一个黑体表面单位面积在单位时间内辐射出的总能量(称为物体的辐射度或能量通量密度)与黑体本身的热力学温度(又称绝对温度)的四次方成正比，即：

式中：为黑体辐射系数，绝对黑体的=1；为斯特藩-玻尔兹曼常量，自然界中一般取=5.67×10W·m·K(参考2010年数据)。

将图4中计算数据代入公式(11)得辐射温度≈350 K，另根据当日天气，设起始温度为300 K，经计算得到太阳辐射对露天试车台温度影响分布，如图5 所示。图中，为使仿真结果更直观，云图倒置给出。可以看出，太阳辐射使露天试车台温度分布不均，向阳面温度高于背阳面温度。露天试车台结构因温度不同产生热应力，将对试车台的试车能力产生一定影响。

图5 太阳辐射对露天试车台温度影响分布Fig.5 Distribution of the effect of solar radiation on the temperature of the open-air test bench

3.3 太阳辐射对露天试车台变形的影响

将太阳辐射对露天试车台温度的影响数据代回ANSYS workbench Static Structural模块中，导入温度分布数据后，计算露天试车台产生的变形及其等效应力分布。经计算，露天试车台因温度变化，导致在竖直方向(方向)，发动机轴向(方向)，发动机径向(方向)分别伸长0.033%、0.107%和0.020%。、、方向形变与角度变化如图6所示，等效应力分布如图7所示。其中，角度变化计算公式为：

图6 露天试车台不同方向的形变与角度变化云图Fig.6 Cloud diagram of deformation and angular variation in different directions of the open-air test bench

图7 露天试车台等效应力分布云图Fig.7 Equivalent force distribution cloud of open-air test bench

式中：Λ，Λ，Λ分别为、、方向角度变化；_，_，_分别代表、、方向形变；为模型角度计算半径。

3.4 热膨胀现象对比验证

线膨胀系数指固体物质在每升高或降低1℃时，其长度的变化量与原温度下长度之比值。根据表3中常见金属线膨胀系数，取钢材的线膨胀系数为18×10/℃。根据模型实际尺寸，取露天试车台主体台架上10个采样点与计算结果对比，ANSYS仿真结果与热膨胀系数法计算结果如图8 所示，两者对比结果如表4 所示。可见，仿真结果与计算结果曲线趋势一致、数值吻合良好，且随着取样点高度的增加，两者误差逐渐降低。最低点误差为11.58%，最高点误差仅为1.67%。露天试车台整体变形平均误差为6.52%。综上说明，本文数值模拟方法可以用于露天试车台受太阳辐射影响计算。

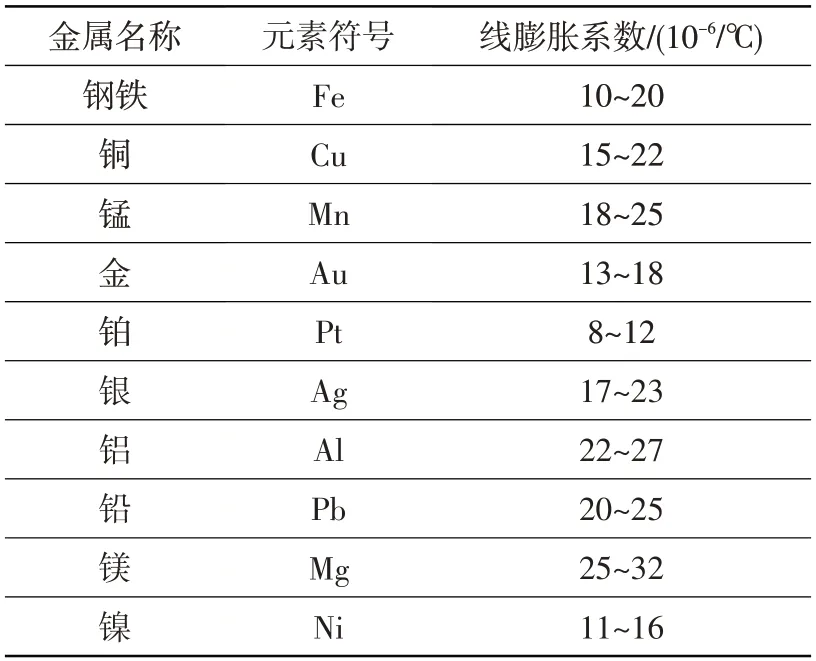
表3 常见金属线性膨胀系数表Table 3 Table of linear expansion coefficients of common metals

图8 ANSYS仿真结果与热膨胀系数法计算结果对比Fig.8 ANSYS simulation results and thermal expansion coefficient method calculation results

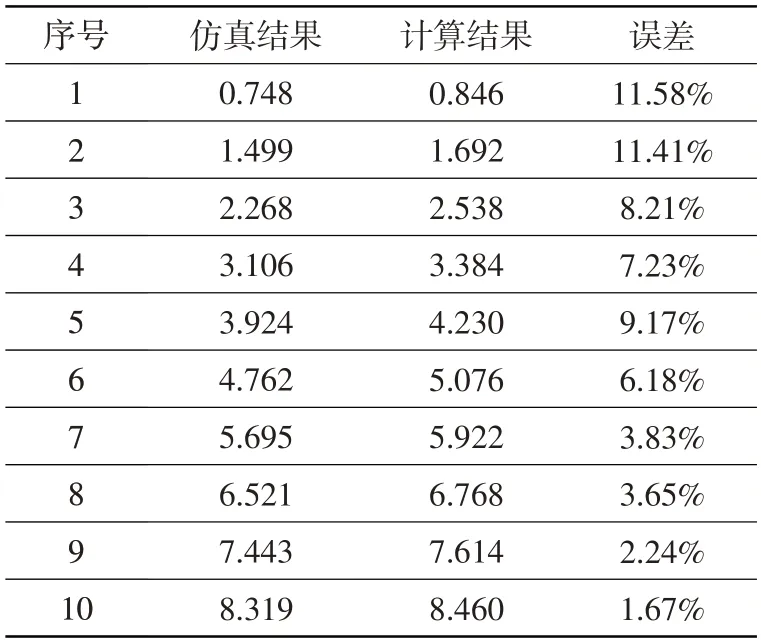
表4 ANSYS仿真结果与热膨胀系数法计算结果参照表Table 4 Comparison of ANSYS simulation results and thermal expansion coefficient method calculation results reference table

4 结论

为分析和确定航空发动机露天试车台在露天环境下试车时，因阳光照射产生热胀冷缩现象对试车台的影响，以6 月21 日13 时为例，对太阳辐射模型所产生的温度场进行探究，并计算温度变化产生热胀冷缩现象的模型形变程度，获得以下结论：

(1) 数值模拟结果较好地反映了因阳光照射航空发动机露天试车台所产生的不均温度分布，考虑了阴影遮挡、天气条件及未经阳光照射的初始环境温度等因素，解释了航空发动机露天试车台试车过程中因环境因素产生的数据误差。

(2) 利用ANSYS workbench 中Solar Calculator功能模块与利用ASHRAE 模型计算的不同环境温度下太阳辐射强度间的误差低于5.20%，Solar Calculator功能模块的计算结果准确有效。

(3) 因阳光照射航空发动机露天试车台表面，产生的温差引起的热胀冷缩现象明显。其中，竖直方向产生的形变程度最大，最大变形处伸长量可达原模型的0.033%；发动机轴向产生的形变程度次之，最大变形处伸长量可达原模型的0.107%；发动机径向产生的形变程度最小，最大变形处伸长量可达原模型的0.020%。

(4) ANSYS 仿真计算结果与热膨胀系数法计算结果曲线趋势一致，数据吻合良好，平均误差为6.52%，建模与计算方法可靠。