软岩隧道衬砌内力计算与开挖过程数值模拟

韩 峰

(中铁十九局集团第三工程有限公司 辽宁沈阳 110136)

1 引言

随着我国公路网建设的不断完善，隧道建设数量和里程不断增加，地质条件复杂多变成为我国隧道建设最鲜明的特点。衬砌结构作为防止围岩变形或坍塌的永久性支护结构，衬砌内力计算的准确性对于工程安全十分重要[1－3]。而针对隧道开挖过程中可能发生的各种隧道病害，可通过数值模拟在极大程度上得以预测，做到提前防护。本文基于阳宗隧道衬砌内力计算和GTS NX验算结果进行对比分析，并针对CD工法单次开挖循环进尺进行数值模拟，以期对隧道衬砌结构设计提供理论支持。

2 工程概况及衬砌内力分析

阳宗隧道位于云南省昆明市澄江县，隧道整体处于近似南北走向的脊状山群地形中，地形较陡，沟谷切割较深，隧道穿越8条断层带，围岩主要为白云岩和泥岩夹杂交替，部分含砾粉质黏土、角砾，局部段落出水量较大。本隧道为左右分离式双洞特长隧道，右线隧道起讫里程为K42＋313～K50＋026，全长7 713 m，左线隧道起讫里程为ZK42＋250～ZK50＋023，全长7 773 m，隧道最大埋深572.62 m。根据«公路隧道设计规范»(JTG D70—2—2014)[4]，隧道围岩级别为Ⅴ级。

2.1 衬砌内力计算

公路等级为山岭一级公路，围岩等级为Ⅴ级，容重为21.2 kN/m3，弹性抗力系数为0.18×106kN/m。衬砌材料选用C30混凝土，材料容重23 kN/m3，弹性模量Eh＝3×107kPa，二衬厚度为d＝0.450 m。采用辛普森法对该隧道典型截面内力进行计算，计算结果见表1。

表1 衬砌总内力计算

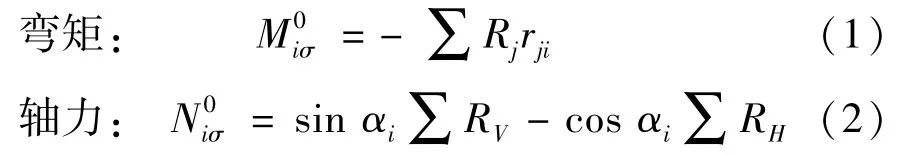
式中:rji为力Rj至接缝中心点ki的力臂。

弯矩、轴力按下式计算:

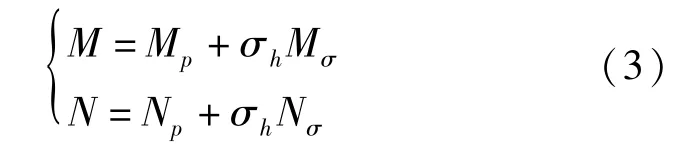
按内力计算结果绘制弯矩图及剪力图，如图1所示。

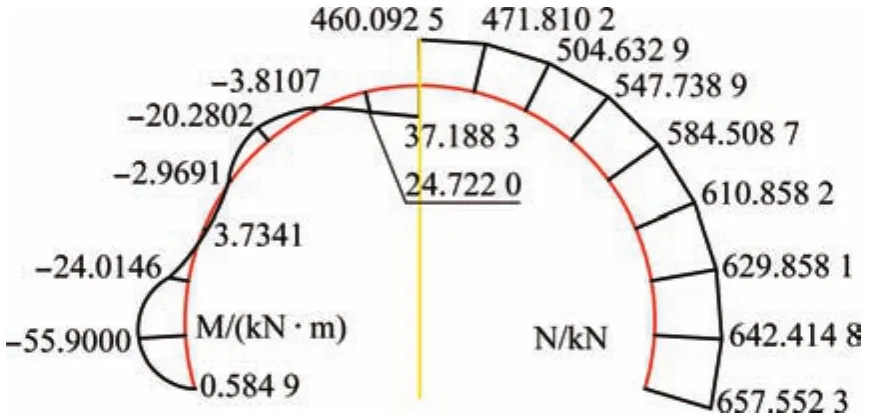
图1 衬砌结构内力

2.2 荷载－结构法计算内力

2.2.1 计算模型

采用荷载－结构法进行衬砌内力计算。计算选用MIDAS GTS NX结构有限元分析软件进行。将衬砌简化为1D梁单元，梁轴线为二衬中线，围岩抗力用曲面弹簧单元模拟，曲面弹簧铰接在弹性抗力区衬砌梁单元的节点上，因此该单元仅在受压时承受轴力，而受拉时失效且不承受弯矩，荷载计算模型如图2所示。

图2 有限元计算荷载简图

2.2.2 结构内力结果

衬砌内力计算结果如图3所示。根据图3可知，轴力最大值出现在仰拱底部，轴力值为－633.475 6 kN；隧道拱顶正中轴力最小。拱顶内侧正弯矩最大值为116.435 6 kN˙m；仰拱内侧负弯矩最大值为－85.631 0 kN˙m。

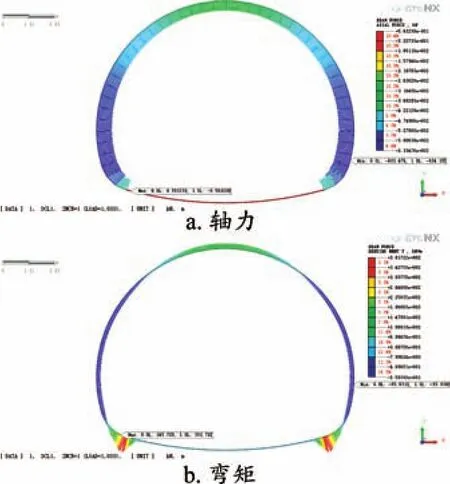
图3 隧道衬砌结构内力

3 隧道开挖数值分析

3.1 模型建立

采用FLAC3D有限差分软件进行CD法施工方案模拟。由于隧道纵向尺寸较长，横断面尺寸较小，故在研究过程中无需考虑开挖进尺对施工的影响[5－6]。取沿隧道纵深方向10 m长的Ⅴ级深埋围岩作为分析对象，隧道宽、高分别为11.2 m、8.8 m，模型横向考虑10倍洞径，竖向考虑6倍洞径，模型尺寸为(100×10×60)m。上部为自由边界，其余均为法向约束边界。

建模采用zone单元，对模型进行分组，选择摩尔－库伦本构模型实体单元，按工程实际参数对围岩进行参数赋值，具体参数见表2。开挖时采用null空壳模型，支护采用 shell壳体单元[7－8]。在隧道拱顶、拱底中点、两侧拱腰分别布置监测点[9]。模型如图4所示。

图4 计算模型

表2 围岩物理指标

3.2 隧道围岩位移分析

在进行隧道开挖时，位移的变化往往能简单明了地体现隧道围岩稳定性。由于隧道的纵向尺寸比横向断面尺寸大，因此主要分析隧道开挖过程前后隧道围岩的竖直位移和水平位移[10]。

3.2.1 竖向位移分析

拱顶竖向位移最大，其次是拱底。随着开挖进行，拱顶和拱底位移也随之不断变大，且拱顶位移增量比拱底位移增量大，施加初期支护后的围岩位移有所减小，但不明显。在截面2开挖完成后下部土体位移有所减小，原因是截面2开挖完成后左侧孔道受力类似于压力拱，导致位移有所减小。开挖完成后在拱底处出现了底鼓现象。由图5可知，各监测点位移在开挖阶段变化较大，在支护阶段趋于稳定，其中监测点1为负，其余监测点为正，说明拱顶竖向向下位移，而两拱腰位置竖向向上位移，拱底竖向位移向上。由监测曲线可知，隧道各监测点的竖向位移在开始开挖后一直发生，直到4号截面的初期支护完成后才趋于稳定，二衬施作后竖向位移增长量较小，结构趋于稳定。

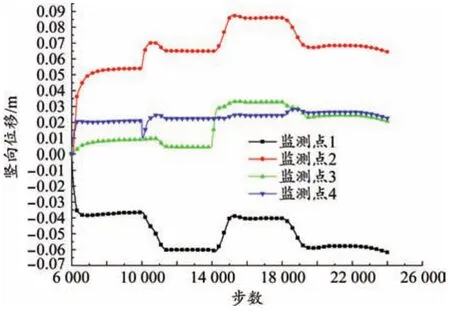
图5 竖向位移监测曲线

3.2.2 水平位移分析

最大水平位移在拱腰处，各以左右拱腰为起点，呈波纹状向两侧扩展，位移大小逐渐减小，其中左侧位移为正(向右)，最大值为56.5 mm，右侧位移为负(向左)，最大值为54.9 mm。当隧道各截面均开挖完成后，围岩水平位移减小，分析原因为开挖后围岩满足了压力拱成拱条件，隧道可以看作一个拱形结构，可将其受到的力转化为推力，导致围岩发生向外的位移。围岩最终位移量为56.4 mm。由图6可知，监测点1和监测点2的水平位移在开挖截面1和截面2时发生了少量向左的水平位移，但随着截面3和截面4开挖完成，水平位移逐渐趋于0。两拱腰处发生的水平位移较大，且方向相反，数值大致相等。

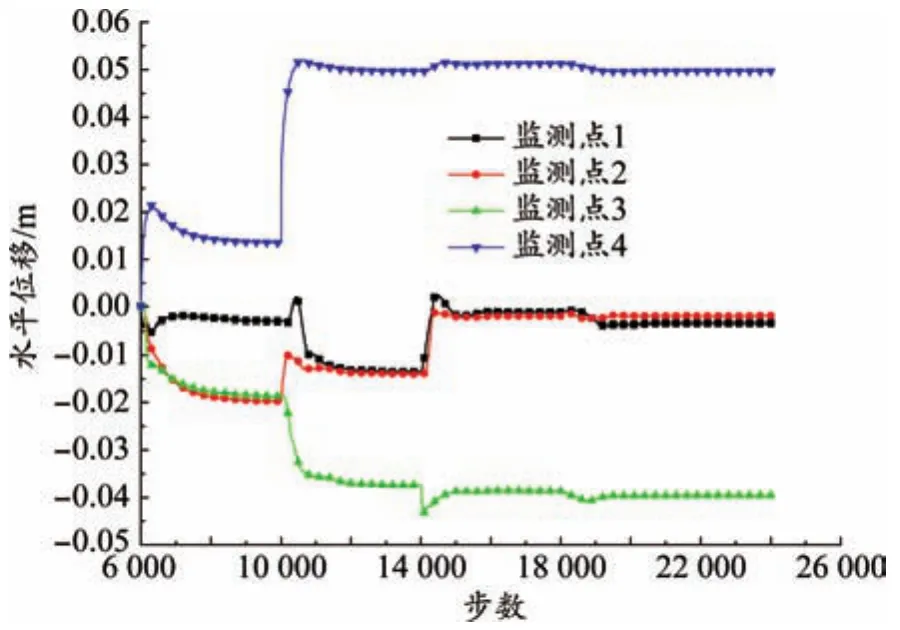
图6 水平位移监测曲线

3.3 隧道围岩应力分析

随着隧道开挖的进行，隧道围岩受到扰动作用，原有的围岩应力平衡状态被破坏，围岩应力将重新分布，直至最后形成一个稳定的应力平衡状态。该过程可能会导致围岩局部应力增大，围岩被破坏导致工程事故的发生。因此，隧道围岩应力状态也是隧道施工中要考虑的重要内容[11－12]。

3.3.1 竖向应力分析

时步1开挖后在拱顶位置产生拉应力，拱底位置产生压应力，但当时步2开挖完成后全部变为压应力，这是因为隧道左侧孔道类似压力拱，致使隧道拱顶和拱底成为压力拱的两个拱脚。当时步3开挖后压力拱被破坏，拱顶又出现拉应力，当时步4开挖后压力拱又重新出现，隧道围岩竖向应力全部变为压应力。根据施作初期支护前后对比可知，初期支护对围岩竖向应力影响较小，前后变化不大。开挖完成后最大压应力出现在拱底，大小为1.256 3 MPa。

3.3.2 水平应力分析

隧道在开挖过程中，围岩水平方向应力大部分为压应力，少部分存在拉应力，这与土体本身性质有关[13－15]。在拱顶、拱底和两侧拱腰处先后出现了应力集中现象，为了防止因应力集中而引起破坏，应进行围岩加固。二衬施作后，二衬结构承担水平方向的压应力，最大值出现在拱顶和拱底，向两侧拱腰依次递减。

4 现场监测结果

测点布设在代表性断面关键部位(如拱顶、拱腰、拱脚、边墙仰拱等)，并对各测点逐一进行编号。埋设压力盒时，要使压力盒的受压面朝向围岩。在隧道壁面测量围岩施加给喷砼层的径向压力时，先用水泥砂浆或石膏将压力盒固定在岩面上，再施作喷砼层，避免喷砼与压力盒之间留有间隙，保证围岩与压力盒受压面贴紧。记下压力盒编号，并将压力盒编号用胶带紧密粘贴在测量导线上。测点压力盒布置如图7所示。

图7 围岩测点压力盒布置

在左上台阶完成初期支护后，拱顶位置压力盒处于受压状态，围岩接触压力达0.71 MPa，表明此时拱顶沉降处于急剧变化阶段。而左右侧边墙压力盒测量值基本为零，表明此时由于上台阶开挖，两侧应力基本释放完毕。当第2～3天观测时，左侧土压力盒的压力发生急剧的变化，从0 MPa上升至0.83 MPa，然后再次上升至1.21 MPa左右，说明左侧土压力盒出现了一个应力调整的过程。右侧土压力盒数据出现负值，处于一种受拉状态。通过对比可知，现场监测结果与数值模拟结果比较接近，体现出数值模拟结果可以为实际工程施工提供参考。

5 结论

(1)通过辛普森法和MIDAS GTS NX计算结果分析，拱脚处二衬轴力分别为657.55 kN、633.48 kN，弯矩分别为55.90 kN˙m、46.97 kN˙m，对比计算结果可知轴力相差较小，弯矩相差稍大，分析原因为辛普生法计算时拱顶存在位移而荷载结构法拱顶不存在位移。

(2)通过FLAC3D模拟，围岩拱顶竖向位移最大，其次为拱底；围岩水平位移最终为56.4 mm，发生在拱腰。由于CD法施工开挖次数过多，对围岩扰动增加，故在进行开挖之前，先对拟开挖隧道的围岩进行超前小导管支护以增加围岩强度。

(3)通过围岩应力变化规律可知，在开挖过程中，隧道两侧拱脚、拱顶、拱底先后均出现应力集中现象，这与实际开挖情况相吻合。应力集中现象对工程安全影响很大，容易造成岩体崩塌。所以，根据模拟结果，应对出现应力集中的部位采取加强支护，以保证围岩和支护结构稳定。