节段装配式悬臂混凝土箱形梁桥动力响应分析
2022-09-30姚锁平
姚锁平
(中铁二十一局集团路桥工程有限公司 陕西西安 710065)
1 引言
由于施工质量好、施工成本相对较低、工期短等优势,节段预应力混凝土连续箱梁的预制技术、装配式技术以及接缝施工技术不断发展,要求桥梁在设计时必须有良好的动力特性。国内外学者对桥梁结构动力特性进行了大量试验研究,张玥等[1]研究了高烈度区连续梁桥的地震响应特性。Pekcan[2]研究了三跨连续混凝土箱形梁在不同倾斜角度下的抗震性能。黄新艺[3]研究了移动车辆作用对公路连续梁桥地震反应特性的影响。李敏峰和徐永峰[4]研究了强震区非对称连续梁桥地震响应及性能。冀伟等[5]结合实际模型和有限元计算结果,分析了试验梁的力学性能。Mohseni等[6]通过研究表明主梁反力和剪力的动力影响会随着桥梁跨度的增加而减小。Shao等[7]认为低阶模态在垂直方向主导弯曲模式,而高阶模态主导钢索的振动模式。Zhou等[8]分析了截面滑动刚度与钢-混凝土组合箱形梁的自振频率的数学关系。Xie等[9]提出了一种新型钢-混凝土组合桁架桥。文献[10]研究表明基台和桥面之间的间隙尺寸对基台的被动变形、冲击力及基础剪力的影响最大。Won等[11]提出了一组描述箱形梁桥在AASHTO-LRFD活荷载下的行为方程。Song和Sim[12]分析表明,当包含锚固或模型上翼缘厚度保持恒定时,固有频率会增加。张世蒙[13]考虑三种不同卓越周期地震波,分析行波效应对大跨度悬索桥地震响应的影响。
综上所述,国内外许多学者常采用理论推导和数值模拟的方法进行桥梁结构动力特性的研究,同时提出了许多减震和抗震技术方法,有效地降低了地震动对主梁结构所带来的破坏,但关于装配式悬臂混凝土箱形梁桥地震动响应的研究较少。本文基于装配式悬臂混凝土箱形梁桥,研究结构自振周期与频率,并分析竖向地震作用下节段装配式箱形梁边跨与中跨跨中的变形和加速度及水平地震作用下边墩与中墩墩顶变形和加速度。
2 动力分析方法
2.1 Hamilton原理
根据Hamilton原理和Lagrange泛函的定义,有:

式中:T、U和W分别为体系的动能、弹性势能和外力势能。
体系动能:
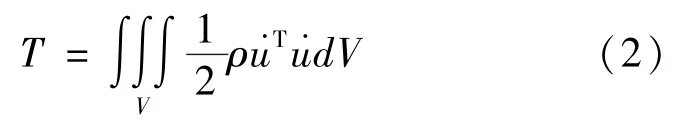
式中:ρ为体系的质量密度;̇u为位移对时间t的一阶导数。
体系弹性势能:

式中:ε、σ、D分别为结构应变、应力列向量、弹性常数矩阵。
体系外力势能(不包括阻尼力):
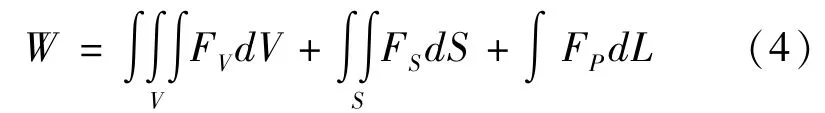
式中:FV为体力向量;FS为面力向量;FP为集中向量。
2.2 结构体系动力学方程
在不考虑阻尼情况下,结构单元体系在等参元分析中有:

式中:ue、N、B分别为单元结构位移向量、函数矩阵、应变矩阵。
将式(5)和式(6)代入式(2)~式(4),可得T、U、W的表达式,然后再代入式(1)和式(2)得:

式中:Me、Ke、Re为结构的单元质量、刚度矩阵、节点力。
局部坐标系下,由式(7)得到结构单元动力学方程:

通过叠加,得:

3 地震波
对多遇地震与罕遇地震动加速度峰值进行适当调整,即:
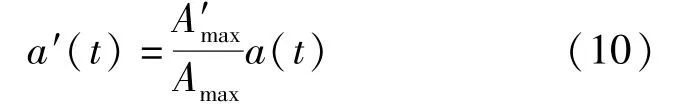
式中:a′(t)为调整后的地震动加速度曲线;A′max为调整后的地震动加速度峰值;a(t)为原地震动加速度曲线;Amax为原地震动加速度峰值。
考虑场地所在地为郑州市地区,选取地震波为EL-Centro波和人工波。地震波持续时间选为30 s,该地区的抗震设防烈度选用8度。地震加速度时程曲线见图1。
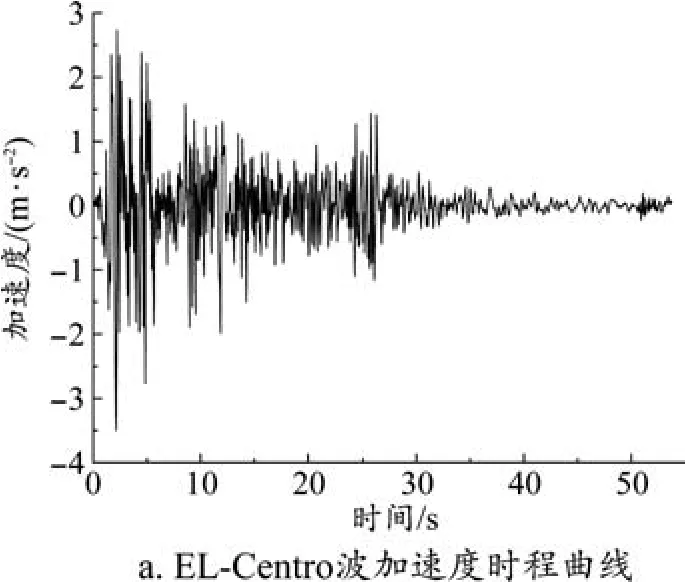

图1 EL-Centro波和人工波加速度时程曲线
4 桥梁结构地震动响应
4.1 有限元分析模型
本项目位于郑州市黄河南岸,主跨为3×46 m节段预制装配式连续梁桥,截面类型为单箱单室。所有节段悬臂混凝土箱形梁高度均为2.20 m,顶板长度均为16.5 m,底板长度均为2.80 m。在工程中过渡节段和标准节段组成预制节段,其宽度均为2.90 m。1号与2号块节段梁体为过渡节段,如图2所示,梁体腹板厚度分别为600、490 mm,底板厚度分别为400、335 mm;3号~7号梁体为标准节段,腹板厚度为380 mm,底板厚度为270 mm。
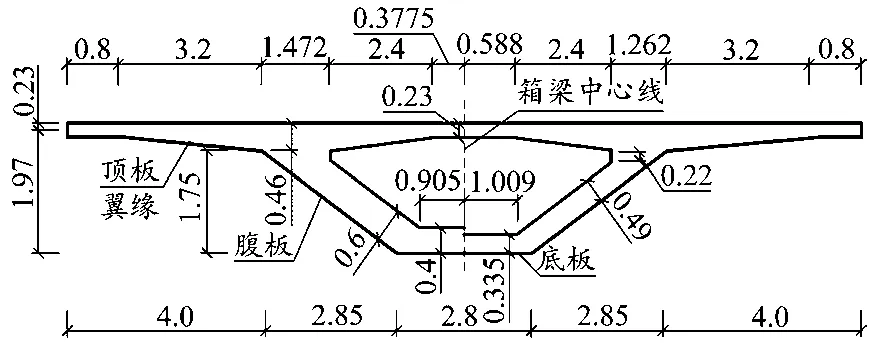
图2 1号和2号块梁体截面(单位:m)
4.2 模态分析
通过有限元法对节段预应力混凝土箱形梁桥进行数值分析,研究在边跨支架法装配式施工和“T”型龙门吊悬臂装配式施工时节段预应力混凝土箱形梁桥的自振频率。由于该桥梁自振频率较多,一般主梁结构前七阶振型较为重要,如图3所示。由表1可知,该节段预应力箱形桥梁的动力特性有以下特点:

图3 节段预应力箱形梁前七阶振型
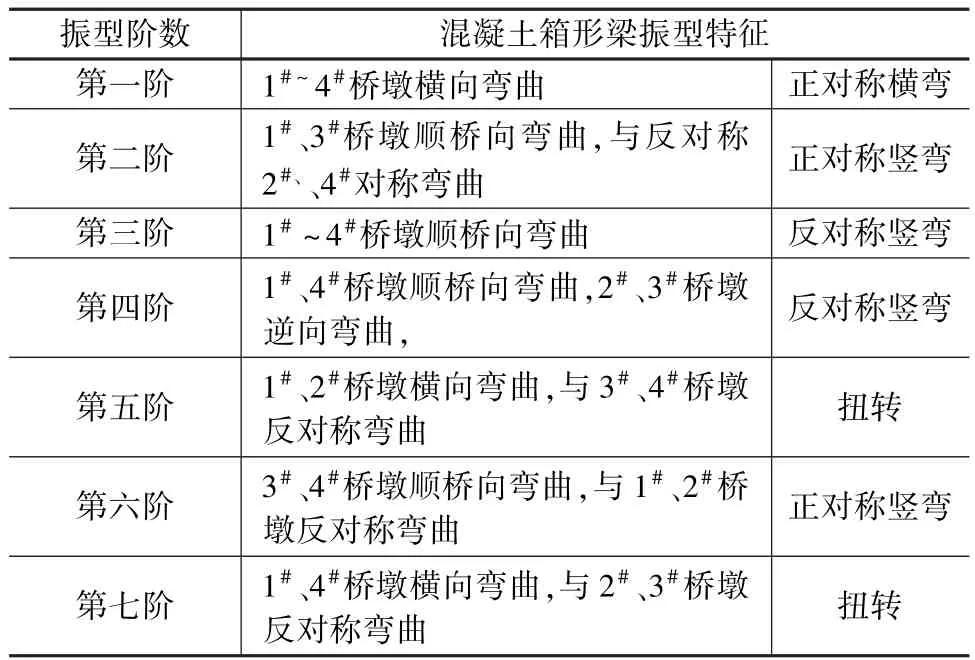
表1 七阶振型描述
(1)节段箱形梁桥主要振型为扭转弯曲,其次为竖向弯曲,由此可知节段箱形梁桥的扭转刚度小,竖向刚度次之,横向刚度最大。因此在节段箱形梁桥设计时,需考虑扭转弯曲稳定问题。
(2)随着主梁振型数增加,节段预应力箱形梁振型形状也变得愈发复杂。
(3)该桥基频为2.142 1 Hz,其一阶的自振频率较大。
4.3 竖向地震动响应
(1)位移计算结果
由图4可知,在竖向地震波激励下,节段箱形梁桥边跨跨中截面在EL-Centro波下,竖向位移峰值出现在2.6 s处,其值为14.76 mm;在人工波作用下,竖向位移峰值出现在10 s处,其值为14.3 mm。节段箱形梁桥的中跨跨中截面在EL-Centro波作用下,竖向位移峰值出现在2.4 s处,其值为22.66 mm;在人工波作用下,竖向位移峰值出现在10.5 s处,其值为20.3 mm。

图4 EL-Centro波和人工波下竖向位移时程曲线
EL-Centro波在0~5 s区间范围内,边跨与中跨跨中竖向位移不断增大,在10 s之后逐渐减小,由此可知在竖向地震作用下节段箱形梁桥中跨的地震动响应稍大。
(2)加速度计算结果
由图5对比可知,在竖向地震波激励下,节段箱形梁桥的边跨跨中截面在EL-Centro波作用下,竖向加速度峰值出现在2.4 s处,其值为8.33 m/s2;在人工波下,竖向加速度峰值出现在3 s处,其值为5.24 m/s2。节段箱形梁桥的中跨跨中截面在EL-Centro波下,竖向加速度峰值出现在2.4 s处,其值为9.79 m/s2;在人工波下,竖向加速度峰值出现在10.5 s处,其值为7.12 m/s2。

图5 EL-Centro波和人工波下竖向加速度时程曲线
地震波在0~5 s区间内,边跨与中跨跨中的竖向加速度不断增大,在10 s之后逐渐减小,对比可知中跨的地震动响应稍大。
4.4 水平地震动响应
(1)位移计算结果
由图6对比可知,在水平地震波激励下,箱形梁桥1#墩墩顶截面在EL-Centro波下,水平位移峰值出现在2.6 s处,其值为11.37 mm;在人工波下,水平位移峰值出现在10 s处,其值为9.64 mm。箱形梁桥2#墩墩顶截面在EL-Centro波下,水平位移峰值出现在2.6 s处,其值为11.90 mm;在人工波下,水平位移峰值出现在10 s处,其值为9.62 mm。
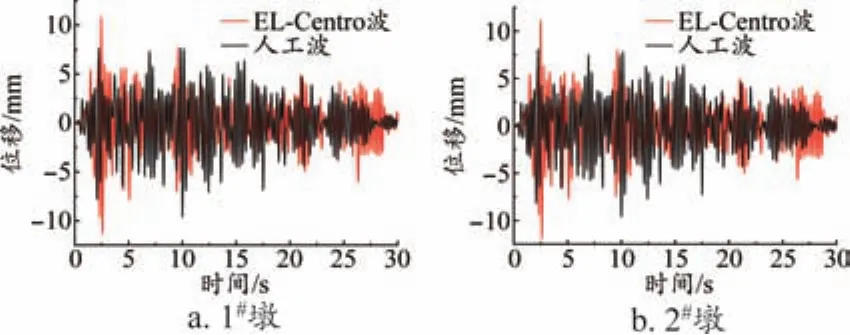
图6 EL-Centro波和人工波下水平位移时程曲线
地震波在0~10 s区间内,1#墩和2#墩顶部节点水平位移最大,在10 s之后变化趋于稳定。表明1#墩和2#墩顶部节点水平位移差异不大,2#墩墩顶节点的地震动响应稍大。
(2)加速度计算结果
由图7对比可知,在水平地震波激励下,箱形梁桥1#墩墩顶截面在EL-Centro波下,水平加速度峰值出现在2.4 s处,其值为8.39 m/s2;在人工波下,水平加速度峰值出现在10 s处,其值为4.41 m/s2。箱形梁桥2#墩墩顶截面在EL-Centro波下,水平加速度峰值出现在2.4 s处,其值为8.34 m/s2;在人工波下,水平加速度峰值出现在10 s处,其值为4.72 m/s2。
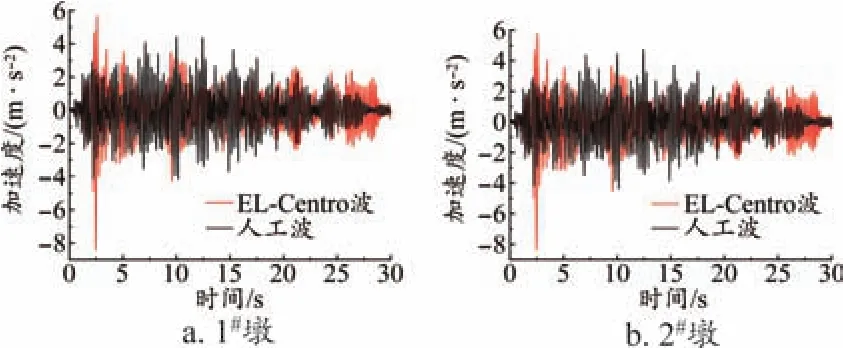
图7 EL-Centro波和人工波下水平加速度时程曲线
地震波在0~10 s区间内,1#墩和2#墩顶部节点水平加速度最大,在10 s之后1#墩和2#墩顶部节点水平加速度的变化趋于稳定。表明1#墩和2#墩顶部节点水平加速度差异不大,1#墩顶节点的地震动响应稍大。
5 结论
(1)研究发现节段装配式悬臂混凝土箱形梁桥的竖向弯曲变形比横向弯曲变形更大,竖向刚度小而横向刚度大;节段装配式悬臂混凝土箱形梁桥的振型类型主要有扭转弯曲、竖向弯曲,在模拟过程中随着振型阶数增加,振型形状也变得愈发复杂。
(2)竖向地震作用下,地震波在0~5 s区间内,边跨与中跨跨中竖向位移和竖向加速度不断增大,在10 s之后边跨和中跨跨中截面的竖向位移和竖向加速度逐渐减小,中跨跨中顶板截面竖向位移稍大;EL-Centro波作用下边跨和中跨竖向加速度差异稍大,人工波作用下边跨与中跨竖向加速度差异不大。
(3)水平地震作用下,地震波在0~10 s区间内,1#墩和2#墩顶部节点水平位移和水平加速度最大,在10 s之后1#墩和2#墩顶部节点水平位移和水平加速度的变化趋于稳定。1#墩和2#墩顶部节点水平位移和水平加速度差异不大。
