基于Douglas-Peucker和Quick Bundles算法的水上交通模式识别

陈信强，徐祥龙，彭静，孙洋，王梓创，阎莹

(1.上海海事大学 a.物流科学与工程学院; b.商船学院，上海 201306；2.长安大学运输工程学院，西安 710064)

0 引 言

随着经济全球化的进一步发展，航运业已经成为经济和社会发展的重要载体。十九大报告提出“加快建设海洋强国”，进一步促进了我国水上交通的发展。船舶交通流量的快速增长导致海上通航环境日趋复杂，给水上交通监管部门和船上工作人员带来了全新挑战。交通模式识别技术用来从移动对象的空间轨迹信息中挖掘并提取交通参与者主要的活动规律，是交通需求分析、交通规划和交通管理的基础。与道路交通和轨道交通等不同的是，水上交通没有明确的物理航道边界。因此，利用船舶航迹数据高效、准确地挖掘水上交通模式，帮助交管部门研判水上交通态势，及时制定交通管控措施，也成为海事领域的一个研究热点。

ZHANG等基于船舶自动识别系统(automatic identification system，AIS)数据设计了一种狭水域通航条件下的船舶轨迹时空分析方法，用于分析交通需求和交通状态等的时空变化规律。李爽等提出一种结合滑动窗口算法和改进谱聚类算法的航路识别框架，实现对船舶航路的辨识。王震等、万辉等和ZHAO等采用道格拉斯-普克(Douglas-Peucker，DP)压缩算法对AIS数据进行稀疏处理，并基于船舶航迹和交通流密度等因素对船舶行为特征进行分析。王壮等基于船端数据和气象数据建立通航环境数据库，并通过改进的均值聚类算法实现对船舶通航环境的智能识别。WANG等提出一种基于Hausdorff距离和具有噪声的基于密度的聚类方法，结合船舶形状特征对船舶航迹进行自适应聚类，并引入综合聚类性能指标对聚类结果进行优化。GAO等首先利用AIS数据对船舶航迹进行分段并编码，然后采用分布邻域嵌入算法对编码数据进行降维，最后基于谱聚类算法实现船舶行为模式识别。

部分学者基于水上交通模式识别的思路对船舶异常行为检测和航迹预测等问题展开了相关研究。ZHEN等首先根据AIS数据的空间和方向特征设计了一种船舶航迹的相似性度量方法，然后利用层次和中心点聚类方法对船舶交通模式进行建模和学习，最后利用贝叶斯分类器对船舶行为进行分类和检测。ARGUEDAS等基于历史自报定位数据(如AIS数据)自动生成水上交通监控网络，为海上交通的实时自动监控、异常检测和交通态势判断奠定了基础。XIAO等、ZHAO等、张春玮等、周海等提出一种基于密度的噪声应用程序空间聚类算法以获取船舶航行模式，并进一步做了船舶运动行为分析、船舶异常检测等。SHENG等提出一种无监督学习方法从AIS数据中挖掘船舶交通模式，并根据船舶航迹特征对不同的航路进行自动分类。

在上述研究中：当航迹样本数据分布不均匀时，具有噪声的基于密度的聚类方法对船舶航迹的聚类效果不理想；基于Hausdorff距离的方法虽然能够对船舶航迹进行聚类，但时间复杂度较高；将船舶单次航迹分解为若干子轨迹后再聚类，不能充分挖掘船舶航迹变化规律。基于此，本文提出一种融合DP算法与快速捆绑包(Quick Bundles，QB)算法的船舶交通模式挖掘框架。该框架首先基于DP算法对AIS数据进行压缩，以解决数据冗余和计算开销问题；然后在QB算法中引入基于最小直接翻转距离的聚类评价指标,以简化不同船舶航迹相似性的计算过程，准确实现水上交通模式识别。

1 基于DP和QB算法的水上交通模式识别

1.1 航迹压缩算法

AIS设备被广泛安装于各种航行船舶，AIS数据更新频率与船舶航行速度成正比(航行速度快，则更新频率高)。由于AIS数据更新速度快(近海在航船舶数据每隔2 s～10 min更新一次)，产生了海量的AIS数据，对水上交通态势感知、船舶航迹预测等相关研究提出了新的挑战。为此，引入轨迹压缩算法剔除冗余数据，在保留船舶航迹数据特征的前提下，实现快速辨识船舶航迹的目的。

DP算法采用“以直代曲”的思想，保留关键航迹点，舍弃非关键航迹点，最终实现船舶航迹数据压缩的目的。假设船舶某航次的航迹如图1所示，用DP算法实现航迹压缩的基本步骤如下：

连接该航次出发地、目的地两点，标记为线段。

计算船舶航迹曲线上各点与直线的距离，从航迹点中选取出与直线的距离最远的点，并将点与直线的距离记为。

比较距离与预先设定的压缩阈值之间的大小关系。若距离小于等于压缩阈值，则使用线段替代原始的航迹曲线(如图1a所示)；若距离大于压缩阈值，则以点为关键点，将航迹划分为曲线和曲线两段(如图1b所示)，并分别对两段曲线重复步骤1至步骤3。

a)距离d未超过压缩阈值θ

整条航迹按照上述方法处理完毕后，依次连接航迹曲线上的各个关键点，得到原航迹曲线的压缩航迹。

1.2 QB算法

Hausdorff距离函数是描述两组点集之间相似度的一种度量方法，即Hausdorff距离的大小表征两组点集之间的不匹配程度，故现有研究常采用该距离函数作为船舶航迹簇的聚类指标。假设有两组点集={,,…,}和={,,…,}，则这两组点集之间的Hausdorff距离定义为

(,)=max((,),(,))

(1)

(2)

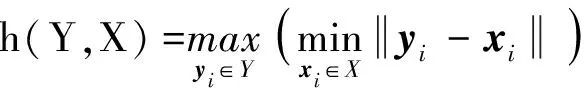
(3)

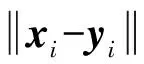
Hausdorff距离函数作为航迹簇的聚类指标存在两个主要缺点：(1)忽略了航迹间的顺序性；(2)算法复杂度高。针对这两个主要缺点，本文提出一种相对简单的最小平均直接翻转距离。对于最小平均直接翻转距离所要求的不同船舶航迹应具有相同数量的样本点，可通过线性插值的方法达到。

考虑到船舶航向因素，对于给定的船舶航迹点集和，其翻转航迹点集分别记为={,-1,…,}和={,-1,…,}，则两条船舶航迹的直接距离、翻转距离和最小直接翻转距离定义如下：

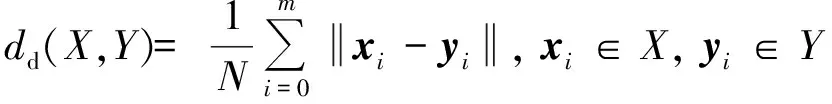
(4)

(,)=(,)=(,)

(5)

(,)=min((,),(,))

(6)

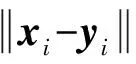
a)直接距离

基于上述对QB算法的介绍，现对船舶航迹聚类算法进行如下描述。在算法的任何一步，均有个簇。如果将一条船舶航迹放至第一簇，则此时=1。

计算船舶航迹(用矩阵表示)与当前所有簇的质心航迹(用矩阵表示)之间的最小直接翻转距离。对不同船舶航迹数据进行重采样操作，使得不同船舶航迹片段均具有相同数量的样本点，以生成相同阶数的聚类矩阵。质心航迹为当前簇中所有船舶航迹矩阵求和后的均值：

=∑/

(7)

式中：是经过重采样后的包含个船舶位置(经纬度)信息的某条航迹数据构成的×2阶的矩阵；为簇内船舶航迹数量。

若与当前所有簇的质心航迹之间的最小直接翻转距离均大于聚类阈值，则创建一个新的簇，并将添加至新簇中；反之，则将添加至与其最小直接翻转距离最小的簇中。

2 实例验证与分析

为验证本文提出方法的有效性，选取两片水域作为研究对象：东经121°56′～122°12′、北纬30°30′～30°43′范围内的洋山港水域;东经121°40′～122°21′、北纬29°38′～30°06′范围内的舟山水域。对于洋山港水域，选取2019年11月212艘船的1 056条船舶航迹数据作为实验数据源；对于舟山水域，选取2021年6月19—21日286艘船的852条船舶航迹数据作为实验数据源。

由于原始AIS数据混合了不同船舶、不同航次的航迹信息，不能直接用于船舶航迹分析研究，所以需要根据水上移动通信业务标识码(maritime mobile service identify，MMSI)、速度特征和时间间隔建立轨迹分割机制。首先对原始数据按照船舶的MMSI进行初步拆分，然后对同一艘船的不同航次数据进行二次拆分。具体来讲，若同一艘船的相邻两个航迹点的时间戳间距大于5 h，则将这两个航迹点信息视为同一艘船不同航次的航迹信息，并进行二次拆分。

由于船舶航速相对较低、AIS数据更新频率较高，故原始数据中存在大量冗余数据。为减小计算开销，需要通过提取船舶航迹关键点的方法来简化船舶的航迹信息。为验证不同算法的船舶航迹数据压缩性能，首先分析DP算法和滑动窗口算法在不同压缩阈值下的压缩效果。以洋山港水域的船舶航迹数据为例，当压缩阈值设置为4 m时，滑动窗口算法的压缩率约为DP算法压缩率的2/3(DP算法压缩率为88.10%，滑动窗口算法的压缩率为63.50%)，但是滑动窗口算法的压缩误差是DP算法的3倍。即在压缩阈值相同的条件下，滑动窗口算法是以损失船舶航迹数据压缩精度为代价提升数据压缩率的。当压缩阈值为8 m和12 m时，DP算法与滑动窗口算法的压缩率和压缩误差呈现出类似的分布规律。基于此，认为DP算法对船舶航迹数据的压缩效果优于滑动窗口算法。DP算法与滑动窗口算法对洋山港水域船舶航迹数据的压缩性能对比见表1。

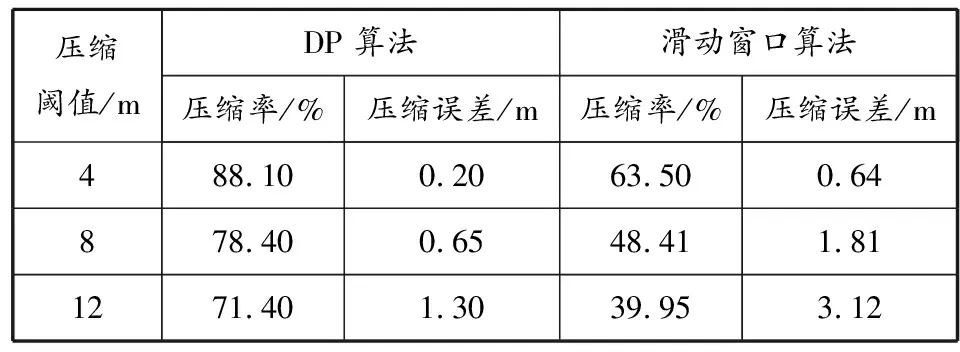
表1 不同压缩阈值下DP算法与滑动窗口算法对洋山港水域船舶航迹数据的压缩性能对比

为确定DP算法的最佳压缩阈值，以0.5 m为步长，分别测试压缩阈值分别为0，0.5 m,…,20 m时DP算法的压缩效果，结果见图3。当压缩阈值增加至12 m时，压缩率为71.4%，压缩误差达到1.3 m；随着压缩阈值的进一步增大，船舶航迹数据的压缩率变化缓慢，但数据的压缩误差急剧增大。综合考虑压缩率和压缩误差等因素，本研究设置压缩阈值为12 m。

图3 不同压缩阈值下DP算法的船舶航迹数据压缩率和压缩误差

为进一步验证压缩阈值设置的合理性，从研究水域内各选取1条典型船舶航迹进行分析,分析结果如下：

(1)在洋山港水域内，MMSI为413427690的船的航迹压缩效果见图4。当压缩阈值为8 m时，压缩率为53%，压缩误差为0.91 m；当压缩阈值为12 m时，压缩率为44%，压缩误差为1.93 m。

a)压缩前航迹

(2)在舟山水域内，MMSI为351372000的船的航迹压缩效果见图5。当压缩阈值为8 m时，压缩率为54%，压缩误差为0.97 m；当压缩阈值为12 m时，压缩率为43%，压缩误差为2.15 m。通过对比不同压缩阈值下的实验结果不难发现，当压缩阈值为12 m时，不仅能够有效地压缩数据量，而且能够保证良好的精度，同时显著降低了算法的时间开销。

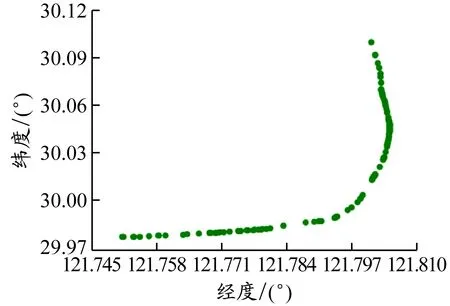
a)压缩前航迹

QB算法要求各航迹具有相同数量的AIS数据点，因此在使用GPS距离定义航迹之间距离函数的基础上，需要对所有船舶航迹进行重采样。选取不同的聚类阈值分别对洋山港水域和舟山水域的船舶交通模式进行分析，聚类结果分别见图6和7。在原始聚类结果中，有一部分聚类簇包含的航迹数量较少，不能作为显著的交通模式，因此建立了航迹簇筛查机制。具体来说，只有包含的航迹数量大于30条的航迹簇，才能可视化到地图上。

a)聚类阈值为2 m

a)聚类阈值为2 m

从船舶航迹聚类结果中不难发现，聚类阈值越小，船舶交通模式的挖掘结果越精细(即航迹簇越多)，其计算开销也越大。然而，阈值较小可能导致大量的小轨迹簇，会对水上交通模式挖掘产生较大的干扰。实验结果表明，洋山港水域在聚类阈值为2 m时，聚类结果较好。洋山港水域的船舶活动规律为：绝大部分船舶活动于中门堂岛和薄刀嘴岛东侧，大洋山北侧、大乌龟岛南侧和西北侧的船舶相对较少。舟山水域为狭水道，船舶的主要运动模式相对复杂，在聚类阈值为4 m时能够挖掘出其主要的航迹规律特征。舟山水域船舶活动规律为：绝大部分船舶往返于涂茨镇东北侧与镇海区或西堠门大桥风景旅游区之间，部分船舶活动于金塘镇的南侧和东北侧、舟山普陀山机场与登步乡之间。

3 结束语

船舶航迹挖掘有助于水上交通监管部门进一步了解海上交通发展态势，及时根据海上交通状况制定合适的交通管控策略(海区通航规划、航路优化等)，有利于识别整体或指定类型船舶的活动规律，为水上交通的精细化管控提供数据支持。本文提出一种基于数据压缩和聚类的水上交通模式识别方法。首先根据船舶航迹数据特征确定DP算法的压缩阈值，然后利用QB算法实现船舶航迹的聚类，最后基于不同水域的AIS数据验证分析方法的有效性。后续研究将结合船舶类型、船舶密度、船舶速度等水上交通特性对船舶交通模式及特征开展进一步的研究和探索。