基于威布尔分布的汽车零部件可靠性分析

刘向阳，韩友国，徐承付，吴洪涛，洪有华，程千伟

奇瑞新能源汽车股份有限公司，安徽芜湖 241002

0 引言

汽车的可靠性是指汽车总成、零部件等产品在规定的使用条件下，达到或超过其完成预定功能的能力，主要反映汽车产品的耐久性、使用经济性和无故障等特点。对于各大车企而言，汽车可靠度的提升，更容易在同类型汽车的竞争中脱颖而出。

1 威布尔分布函数模型

威布尔分布是可靠性分析理论基础，广泛应用在材料和零部件的寿命分析中。因其具有形状参数，可通过改变此参数来表达不同函数的分析模型。从原理上说，威布尔分布应用在损坏后丢弃或更换的零部件，但整个设备仍在正常工作的不可修复产品上。

三参数威布尔分布的概率密度函数()的表达式为：

(1)

累积概率分布函数()的表达式为：

(2)

根据上述概率密度函数的表达式，可得到不同参数、、对威布尔函数()的影响，如图1至图3所示。

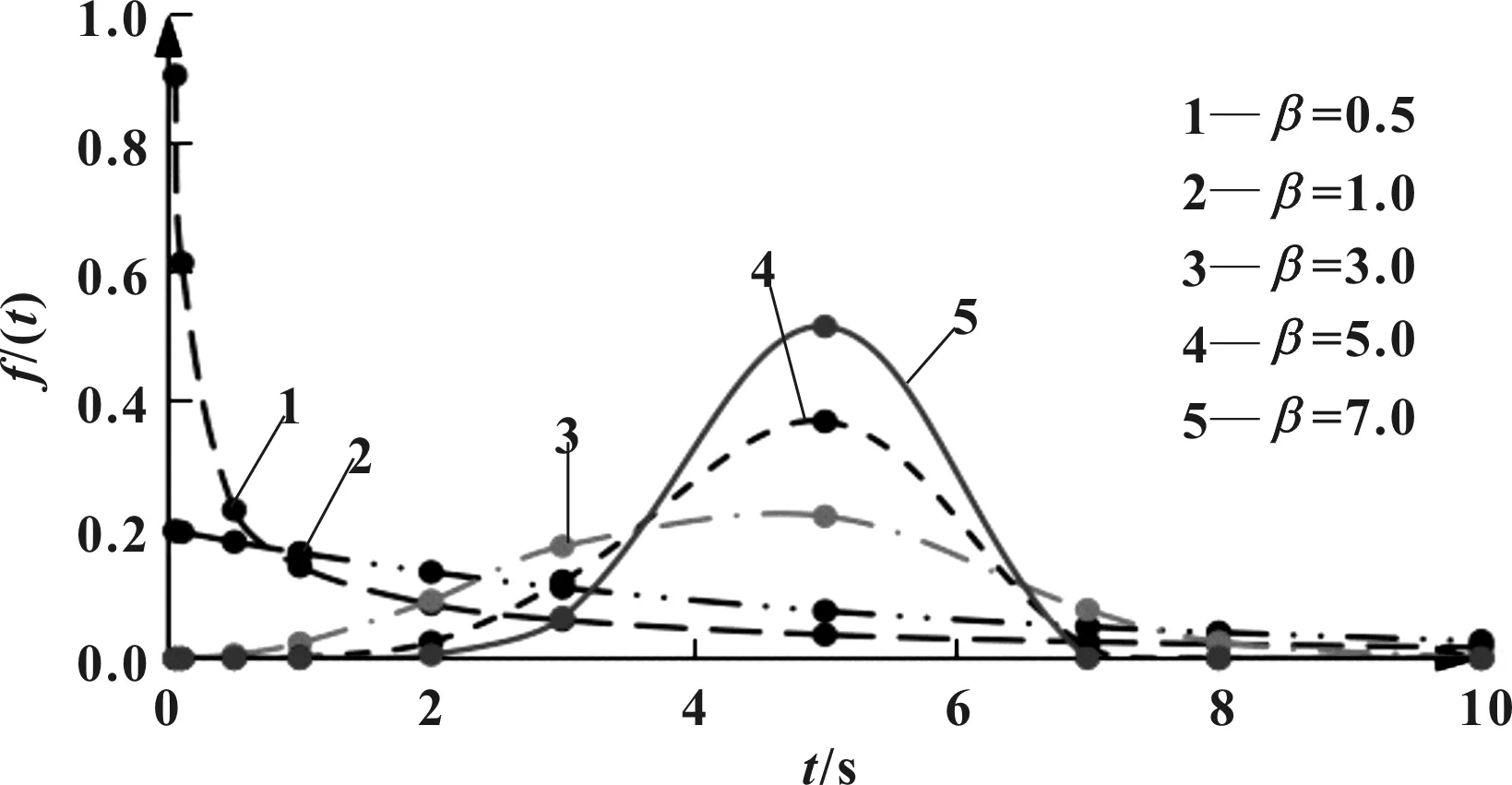
图1 γ=0、η=5.0时β对威布尔分布函数的影响

图2 γ=0、β=3.0时η对威布尔函数的影响

图3 β=2.0、η=2.0时γ对威布尔分布函数的影响

图1至图3中，为形状参数，决定概率密度曲线的形状；为位置参数，也称起始参数，决定参数分布的位置(坐标轴与曲线的相对位置)，在实际工程应用中，一般省去该参数，即最小寿命=0；为尺度参数，决定了632的样本数据在整体空间的分布。

2 汽车产品的可靠度

汽车产品的可靠度(Reliability)是指汽车产品(系统或总成)在规定使用条件下(工作环境)和规定的时间内(某一特定时间持续行驶无故障里程数)，完成规定功能的能力(达到标准、法规及合同规定的功能和性能要求等)。

一般情况下，可靠度函数满足如下关系：0≤()≤1，(0)=1，(+∞)=0。在任意时刻，可靠度函数的表达式为：

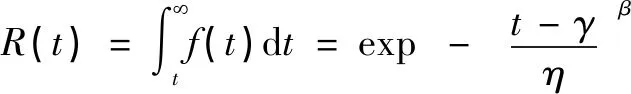
(3)

与可靠度相对应的是不可靠度，又称失效率，一般用()表示，累积失效概率分布函数为：

(4)

根据式(3)和式(4)得到如图4所示的可靠度()和失效率()随时间的变化曲线。

图4 β=2.0、η=2.0时可靠度与失效率关系曲线

由图4可知，汽车产品的可靠度()随着使用时间的增加而不断降低，且随着的持续增加，降低速度趋缓。反之，失效率()随着时间的增加，其增加速度先快后慢。

3 汽车产品的浴盆曲线

大量研究实践表明汽车产品在其生命周期内，故障发生率与使用时间或行驶里程表现极大相关。在实现其功能的过程中使用时间或行驶里程与故障发生率的曲线多呈浴盆状，一般称之为浴盆曲线。

根据工程应用经验，形状参数取不同值时，对产品的可靠性有不同的影响。在整个产品生命周期中，其失效过程主要分为早期失效、偶然失效和耗损失效3个阶段，如图5所示。

图5 浴盆曲线

(1)当<1时，失效率()呈递减分布，适用汽车早期故障的失效建模，主要表现为大批相同产品元件投入使用时，因材料的不均一性和工艺等造成的失效问题；

(2)当=1时，失效率()呈近乎常数分布，适用汽车偶发故障(正常使用期)的随机失效建模，主要表现为早期失效的产品元件被替换后，失效率趋于稳定，少数产品元件在工作中发生不可预测的变化导致失效；

(3)当>1时，失效率()呈递增分布，适用汽车磨损故障的磨耗老化建模，主要表现为产品元件经过长时间工作后，进入磨损老化期而导致的失效问题。

4 设计验证样本容量R-C-N关系

基于上述对汽车产品生命周期内的失效故障分析，需在整车研发设计过程中对其可靠性进行验证。因项目周期、设备资源和成本等因素，一般会根据需要缩减试验样车的验证数量。

在制定试验验证计划过程时可参照经验可靠度，置信度和样本数之间的经验公式：

(5)

当可靠度一定时，样本数与置信度的变化曲线如图6所示。由图可知，要想获得较高的置信度，就需增加样本数。

图6 可靠度R一定时，样本数N与置信度C的变化曲线

当置信度一定时，样本数与可靠度的变化曲线如图7所示。由图可知，要想获得较高的可靠度，也需增加样本数。

图7 置信度C一定时，样本数N与可靠度R的变化曲线

5 案例分析

基于某上市电动汽车2017年1月1日至2017年12月31日所售车辆售后数据，以出现故障次数较多的车辆控制器总成为例，统计在此期间购车且使用时间在1～36个月内的车辆控制器总成的故障个数，具体详见表1。

表1 车辆控制器总成使用月数及故障个数统计

根据表1相关统计数据可得到如图8所示的使用月数与当月故障个数及累积故障数的分布。由图可知，当车辆控制器总成使用在18个月左右时，故障率个数最高，随后故障个数增长趋缓。

图8 使用月数与当月故障个数及累积故障数的分布

根据车辆控制器总成使用月数的累积故障率公式：

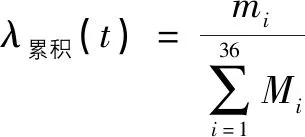
(6)

式中：为使用月时的故障数；为使用月时累积的故障数。

根据式(6)可得到如图9所示的使用月数与累积失效率及可靠度的分布。由图可知，当车辆控制器总成使用月数达20个月左右时，其累积故障率越来越低，表明该零部件处于偶然失效期阶段。

图9 使用月数与累积失效率及可靠度的分布

6 结论

本文基于三参数威布尔分布函数，分析不同参数，，对概率密度函数()的影响。研究了汽车产品可靠度()和失效率()随时间变化的关系，基于浴盆曲线探讨了不同阶段的失效原因及形式。从设计验证角度出发，探讨了可靠度、置信度和样本容量之间的关系。

基于某上市车型2017年的售后数据，以出现故障次数较多的车辆控制器总成为例，分析了在1～36个月的使用周期内故障个数，结果表明：在产品偶然失效期内的车辆控制器的可靠度相对早期失效期的要高。