具有一致精度的薄壳方程的线性有限元方法

张胜

(韦恩州立大学，底特律 密歇根 48202)

1 引言

在Naghdi薄壳模型中，总应变能是弯曲应变能，切向延压应变能和横向剪切应变能的总和.在弯曲为主的变形中，壳的延压剪切应变相对很小，当弯曲的壳无限变薄时延压剪切应变趋向于零.如果把壳的变形限制在分片多项式构成的有限元函数空间里，当延压剪切应变为零时，有限元函数能表示的变形缩减为零.对很薄的壳而言，有限元解给出的变形远小于实际变形.此所谓延压剪切数值闭锁.这个问题的根源在于分片多项式不能准确表达曲面的等距纯弯曲变形.这种失败的数值计算会导致工程师做出错误的关于壳结构强度的判断.

数值闭锁会发生在许多依赖参数的数学物理方程的科学计算中，这包括Timoshenko梁弯曲方程，Timoshenko-Naghdi拱变形方程，Reissner-Mindlin板弯曲方程，忽略了横向剪切应变的 Koiter[1]薄壳方程，更一般的 Naghdi[2]壳方程和其他薄或细的构件的形变力学问题的模型.这些问题中的参数是构件的相对厚度.切向延压闭锁是Koiter壳模型数值计算中的一个主要问题，而横向剪切闭锁一直是Reissner-Mindlin板弯曲模型研究的中心问题.Naghdi薄壳模型则涉及这两种闭锁，而且壳的曲率使这两种闭锁耦合在一起无法分离.平板是曲率为零的特殊的壳，在此情况下Naghdi薄壳模型解耦成Reissner-Mindlin板方程和一个平板切向延压的平面应力方程，对这两者都有几个成功的算法.但两者简单的结合无法产生有效的壳有限元.

对Timoshenko梁弯曲方程而言，在形成刚度矩阵的过程中只须用一个低精度的数值积分方法来计算剪切应变能便可消除剪切闭锁，从而得到最优阶的一致精确的精度不随梁的厚度变化的有限元方法.这个技术早已为结构工程师所知，其数学理论则要用混合有限元方法来建立[3].对于Reissner-Mindlin板，最成功的方法是基于对其变量的重组，把板方程解构成一个摄动过的Stokes方程和Poisson方程，组合其已有的有限元而得到的，参阅文献[4]及其中的参考文献.由于其特殊性，这些方法和理论无法用于薄壳模型.对于薄壳问题，自从有限元创立以来，工程力学界和数学界一直在不断地努力，尽管有大量数值计算的工程文献和很大的进展，可消除闭锁的方法的数学理论还远不如人意[5-8].几个商用软件都有各自的算法，但没有一种方法是有数学基础的或完全可靠的，有时甚至是失败的.

间断有限元(Discontinuous Galerkin简称DG[9])近年来得到了长足的发展.它给选择有限元空间和自由度提供了更灵活的方法，在有些计算问题中，产生了高精度高效率算法.在理论上它有可能把五花八门的有限元纳入一个统一的框架.不少人相信DG具有解决薄壳计算中闭锁问题的潜力[10-11].文献[12]分析了DG方法在解决Koiter壳计算中切向延压闭锁的问题优势.本文讨论Naghdi薄壳模型的最低阶混合DG方法，所用有限元函数均为分片线性函数.对壳中面位移和法向纤维转角用间断函数(在与壳的自由边界相临的单元上须增加一些二次函数)，而对辅助性的延压应力张量和剪切应力向量用连续函数.用Nitsche方法处理固支边界，并绕过了混合有限元方法[13]常用的Babuˇska-Brezzi条件.如果用常规的线性有限元计算Naghdi方程，在以弯曲为主的壳变形问题中会有非常严重的闭锁现象，致使数值结果完全无用.

这里的分析主要针对的是弯曲为主的壳变形问题.需要说明的是有些情况下，壳的变形是以切向延压为主的，这时薄壳具有极高的承载能力.更多的壳变形是介于弯曲为主和延压为主的中间形态，其承载能力高于弯曲的壳，但不如延压壳抗载.壳变形属于何种形态取决于薄壳曲面的形状，加载方式和边界支撑方式.例如，如果壳的中面是直纹面，部分边界是一条直纹线，沿其固支，在横向载荷作用下它的变形便是以弯曲为主.如果壳的中面是椭圆形的，沿整个边界固支，不管如何加载，它的变形都以切向延压为主.如果壳的中面是椭圆形的，沿部分边界固支，其余部分自由，它的变形处于中间形态.能够避免数值闭锁，从而对壳弯曲问题有效的算法是否适用于其它种类的壳变形是计算工程力学中的未曾解决的重大问题.本文亦无意做此尝试.

本文结构如下，在第2节中，引进Naghdi壳模型，引入横向剪切应力向量和切向延压应力张量作为新变量，把壳方程写成混合形式，并给出一些必要解的先验估计.在第3节中，引入有限元模型.在第4节做误差分析.在文中，C代表常数，其值可依赖于壳的曲率和其它几何系数，壳的材料的Lamé系数，和有限元单元形状的规则性有关，但与有限单元的尺寸和壳的厚度无关.用A≾B来表示A≤CB.如果A≾B和A≾B都成立，写成A≃B.用上标表示向量和张量的反变分量，下标表示协变分量.除ϵ外，希腊字母上下标在{1，2}中取值.拉丁字母在{1，2，3}中取值.也采用关于重复上下标的Einstein加法规则，和Sobolev空间中的常用记号.具有协变分量uα或反变分量ξα的向量将分别由粗体字母u或ξ表示.具有分量Mαβ的张量将简称为M.

2 薄壳方程

协变微分的乘法规则，如 (σαλuλ)|β=σαλ|βuλ+σαλuλ|β也是成立的.

映射φ是Ω和之间的一对一对应关系，它把子域τ⊂Ω映射到子区域

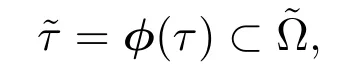
曲线段e⊂映射成曲线段=φ(e).在壳中面上定义的函数f将通过映射φ与Ω上定义的函数认同，并用相同的符号表示.因此f(φ(xα))=f(xα).若无进一步解释，波浪号表示曲面上的量或运算，没有波浪号则表示在平面域Ω上操作.需要使用曲面上的格林公式，反复进行分部积分.对曲面子域，用表示与曲面相切的边界∂=φ(∂τ)的单位法向量.设nαeα是R2中∂τ的单位法向量.这里的eα是R2中的基向量.对于向量场fα，格林公式如下:

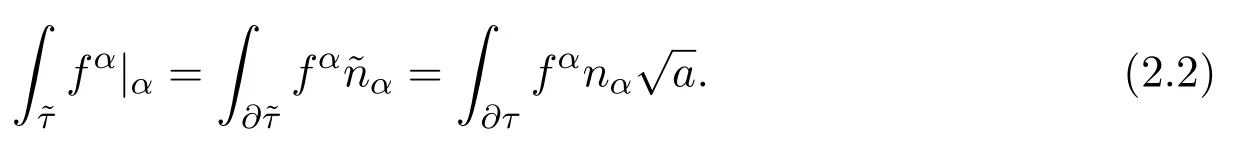
在这里和下文中，为简单计，忽略了积分中的微分元素.第一个积分是关于曲面的面积元的，表达成平面区域τ上的常规积分则是∫第二个积分是根据∂的弧长取的.最后一个是根据弧长∂τ.将使用这样一个事实，在∂τ的直线部分上，nα是常数，而α通常是沿∂变化的.

2.1 Naghdi薄壳模型

Naghdi壳模型[2]使用壳中面的切向位移u=uαaα，法向位移wa3和法向纤维旋转θ=θαaα作为主要变量.用这样一组主要变量，弯曲应变，切向延压应变和横向剪切应变可表示如下:

这个混合模型是有限元方法的基础，它的解由十个定义在二维区域Ω上的函数组成.

2.2 壳厚度趋于零时壳模型解的渐近估计

引用文献[17-18]中的两个结果，得到一些关于Naghdi壳模型的解随壳厚度变化的渐近行为的有用估计，以分析有限元模型.本小节中的符号独立于本文的其余部分.Naghdi壳模型(2.7)可写成如下算子方程(2.12).假设H，U，V是Hilbert空间，A和B是分别从H到U和V的线性连续算子.假设

3 有限元模型

4 有限元法的误差分析

有限元模型(3.9)的稳定性和它与Naghdi壳模型(2.10)的相容性保证了有限元解的最佳逼近性.有限元法的误差分析简化成了一个逼近论问题.对Naghdi壳方程的解，可构造有限元空间的插值函数，从而证明如下定理，它是本文的主要结果.这个定理的证明和相关数值验证可参考文献[12]和它引用的文献.

这个极限是个非零常数.定理4.1意味着有限元解的相对误差具有最优阶的精度.本方法解决闭锁问题的效率从定理中不等式右侧第一个括号中的项可以看出.如果用常规有限元方法这括号中的项将变成[1+ϵ-1]，当ϵ→0这个系数会被无限放大，使计算结果对很薄的壳失效.如果壳变形不是弯曲主导的，则有‖(θ0，u0，w0)‖Hh=0，定理 4.1并不意味着有限元解在相对误差下具有任何精度.