弱罗马图和图的弱罗马控制的一些性质

杨 剑, 李志强

(1. 河南交通职业技术学院公共基础教学部，郑州 450000;2. 河南财经政法大学数学与信息科学学院，郑州 450002)

0 引言

设G=(V,E)是一个顶点集为V，边集为E的图，定义实值函数f:0,1,2}，即对任意的v ∈V，则f(v) = 0 或1 或2。设V0、V1和V2分别表示在上述f定义下取值分别为0、1 和2 的顶点集，即Vi={v ∈V|f(v) =i}，其中i= 0,1,2。注意到，函数f:0,1,2}和顶点集V的划分(V0,V1,V2)是一一对应关系。因此，为了方便亦记函数f=(V0,V1,V2)。

罗马控制理论首先是由Stewart[1]提出的，在此基础上，Cockayne 等[2]给出了罗马控制函数的定义。设图G= (V,E)，令函数f= (V0,V1,V2)，若V0中的每一个顶点都至少与V2中的一个顶点相邻，则称f为图G的罗马控制函数(简称RDF)。函数f=(V0,V1,V2)的权记为

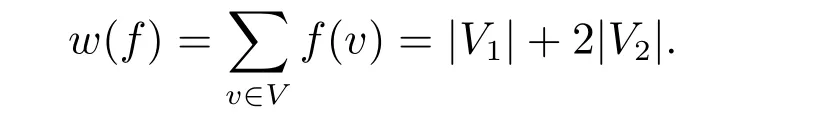
图G的罗马控制函数的最小权称为罗马控制数，记为γR(G)，即

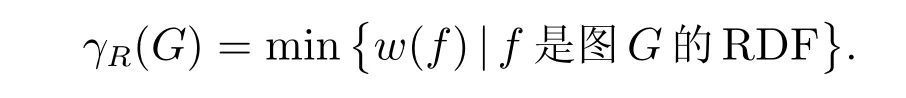
例如，2×5 格子图G2,5的罗马控制数为6，如图1(a)，其中空心圈代表V1中的点，实心圈代表V2中的点，其他为V0中的点。一个权为γR(G)的RDF 称为γR(G)-函数。

罗马控制函数的概念来源于下面的实际问题。设图中的每一顶点代表罗马帝国的一个地区，如果一个地区(顶点v)没有军团驻扎，即f(v) = 0，则称该地区是不安全的，否则(即该地区有一个军团驻扎(f(v) = 1)，或有两个军团驻扎(f(v) = 2))称该地区是安全的。一个不安全的地区(顶点v)能够被安全防御，如果能够从相邻的地区(v的一个邻点u)派一个军团到达该地区。但是在公元4 世纪最高统治者颁布法令：若从一个安全地区派遣一个军团到一个不安全地区使得原地区不安全，则不允许派遣。因此，在派出其中一个军团到相邻地区之前必须在该地区驻扎两个军团(f(v) = 2)。最高统治者利用这种方式能够防御罗马帝国。为了节约军费，统治者想用尽可能少的军团防御罗马帝国。因此，一个权为γR(G)的罗马控制函数就对应着一个最优派遣军团驻扎的方案。

为了进一步探索节约军费开支的方法，同时仍然能够防御罗马帝国，Henning 和Hedetniemi[3]提出了新的策略，给出了弱罗马控制函数的定义。设图G= (V,E)，令函数f=(V0,V1,V2)，若V0中的顶点u不与V1或V2中的任何顶点相邻，则称它是未被防御点。如果函数f=(V0,V1,V2)满足：若V0中的每一个顶点u都至少与V1∪V2中的一个顶点v相邻，并且fu:0,1,2}(fu(u)=1,fu(v)=f(v)−1 且fu(w)=f(w),∀w ∈V −{u,v})没有未防御点，则称f为图G的弱罗马控制函数(简称WRDF)。图G的弱罗马控制函数的最小权称为弱罗马控制数，记为γr(G)，即

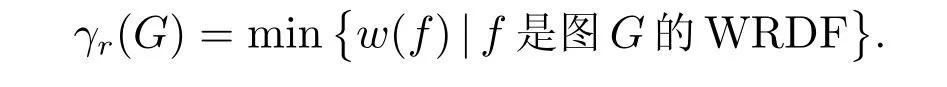
例如，2×5 格子图G2,5的弱罗马控制数为4，如图1(b)。一个权为γr(G)的WRDF 称为γr(G)-函数。

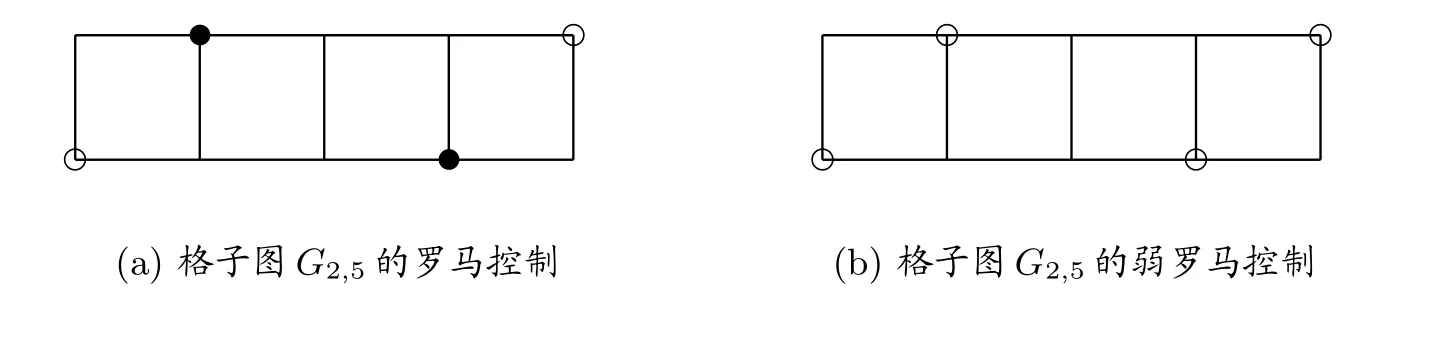
图1 对2×5 格子图G2,5 的构造

Henning 和Hedetniemi[3]基于下面的思想给出了WRDF 的定义。如果一个地区是不安全的(即没有军团驻扎)，且与之相邻的地区也都是不安全的，则称这个地区是未防御的。由于不安全地区是薄弱可击的，所以要求每一个不安全地区都与一个安全地区相邻，并且当这个地区遭到攻击时，从相邻地区派遣军团到此防御，不会产生未防御地区，故每一个不安全地区同样能够进行防御。统治者通过这种方法仍然能够保卫罗马帝国，而这种派遣军团保卫帝国的方案恰好对应着一个WRDF，并且最少军团数目恰好对应着WRDF 的最小权，这种方案既能节约军费又能保卫帝国。因此，弱罗马控制更加重要和实用。

罗马控制是一个有丰富历史背景和数学背景的典型控制问题[1–16]，它与计算机科学、交通安全监管控制、企业安全生产监管控制、组合优化、监视系统和社会网络等领域密切相关，具有重要的理论意义和应用价值。Cockayne 等[2]研究了图的罗马控制，其中包括确定了路、圈、完全n部图和2×n格子图等的罗马控制数，给出了罗马控制数的上、下界，刻画了γR(G) =γ(G),γR(G) =γ(G)+1 和γR(G) =γ(G)+2 的图G的特征，以及γR(T)=γ(T)+1 和γR(T)=γ(T)+2 的树T的特征等。Henning 和Hedetniemi[3]研究了图的弱罗马控制，其中包括确定了路和圈等的弱罗马控制数，刻画了γr(G) =γ(G)的图G的特征等。本文作者也曾研究了图的弱罗马控制，其中包括确定了完全n部图的弱罗马控制数和弱罗马控制数的下界，给出了弱罗马控制数的上界等[5]，刻画了γr(T) =γ(T)的树T的特征[6]以及γr(G) =γ(G)+1 的图G的特征[7]，在文献[8]中确定了2×n格子图的弱罗马控制数，宋晓新等[9]确定了3×n格子图的弱罗马控制数。本文用构造法确定了路P3，星K1,t(t ≥2)，由星K1,t1,K1,t2,···,K1,tn(ti ≥3,i=1,2,···,n)的中心点依次连接成一条路所构成的树T，或由它们的外点连接构成的树T是弱罗马图，并给出了弱罗马图和图的弱罗马控制的一些性质。本文所考虑的图均为有限的非平凡简单图。

1 概念和已知结论

设G=(V,E)是一个顶点集为V、边集为E，且阶数为n的图，v是V的任意一个顶点，顶点v的度记为d(v)。顶点v的开邻域记为N(v) ={u ∈V|uv ∈E}，且闭邻域记为N[v] ={v}∪N(v)。对一个集合S ⊆V，它的开邻域记为N(S) =∪v∈SN(v)−S，且它的闭邻域记为N[S] =S ∪N(S)。设u ∈V,S ⊆V，若N[u]∩S={v}，则称顶点u为v关于S的私有邻点，或简称v的一个S −pn。顶点v的所有S −pn的集合记为pn(v,S) =N[v]−N[S −{v}]，被称为v关于S的私有邻集[4]。我们定义v关于S的外私有邻集为epn(v,S) =pn(v,S)−{v}，简称v关于S的外私有邻点为S −epn，则集合epn(v,S)⊆V −S。如果对于任意的u,v ∈S，使得N[u]∩N[v] =∅，则称S是2-分离集。

设G=(V,E),S ⊆V，若U中的每一个顶点都至少与S中的一个顶点相邻，则称集合S控制集合U，记为S ≻U。如果S ≻V −S，或者N[S]=V，则称S为图G的一个控制集[4]。图G的控制集的最小基数称为最小控制数，记为γ(G)，即

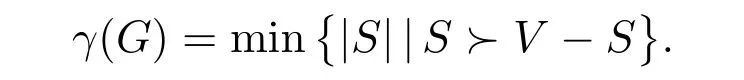
一个基数为γ(G)的控制集称为γ(G)-集。

设T= (V,E)是一个顶点集为V、边集为E，且阶数为n的树，一个度为1 的顶点称为树T的一片叶子(又称为悬挂点)，与叶子相邻的顶点称为树T的支撑点，与至少两片叶子相邻的顶点称为强支撑点。在本文中，记所有支撑点集合为S(T)，所有强支撑点的集合为SS(T)，所有叶子集合为L(T)。若S ⊆V，则以S为点集、S中各点之间的边还保留原树T的边构成的子树，记为T[S]。对于任给的正整数t，完全二部图K1,t称为星，并且称度为t(t ≥2)的顶点为中心点，度为1 的顶点为外点。特别地，在P2中，称两个顶点都为中心点。若图G满足γR(G) = 2γ(G)，则称图G是罗马图。若图G满足γr(G)=2γ(G)，则称图G是弱罗马图。

为了研究问题的方便，下面把与本文有关的已有结论列出来，以便后面使用。

引理1[3]对任意图G，γ(G)≤γr(G)≤γR(G)≤2γ(G)。

引理2[2]图G是罗马图，当且仅当它有一个γR-函数f=(V0,V1,V2)，使得V1=∅。

引理3[2]图G是罗马图，当且仅当

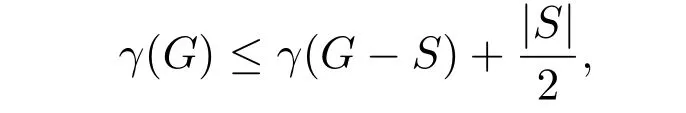
对每一个2-分离集S ⊆V。

引理4[3]如果图G满足γr(G)=2γ(G)，则对每一个γ(G)-集S和每一个v ∈S，外私有邻集epn(v,S)包含两个不相邻的点。

引理5[5]如果图G= (V,E)的阶数为n且包含一个度为n −1 的顶点，则γ(G) =1，并且如果G=Kn，则γr(G)=γ(G)=1；否则γr(G)=γR(G)=2。

引理6[3]对任意的n≥1，有γr(Pn)=「⏋；对任意的n ≥4，有γr(Cn)=「⏋。

引理7[16]对任意的n≥1，有γ(Pn)=「⏋。

2 弱罗马图

在文献[2]中给出了罗马图的两个特征，如引理2 和引理3，在文献[3]中给出了弱罗马图的一个特征，如引理4。下面我们给出弱罗马图的一些性质，对刻画弱罗马图的特征具有重要意义。

定理1对任意的图G= (V,E)，γr(G) = 2γ(G)，当且仅当存在一个γr(G)-函数f=(V0,V1,V2)，使得V1=∅。

证明 (⇒) 若γr(G) = 2γ(G)，设S是G的一个γ(G)-集，则令f= (V0,V1,V2) =(V −S,∅,S)是G的一个WRDF。又

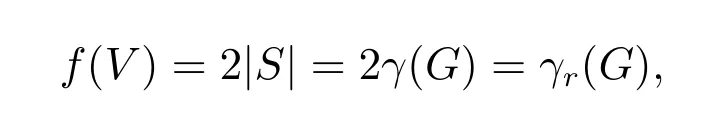
所以f是一个γr(G)-函数，并且V1=∅。

(⇐) 设f=(V0,V1,V2)是一个γr(G)-函数，使得V1=∅。因此γr(G)=2|V2|，又由定义知V1∪V2≻V，所以V2是G的一个控制集。从而γ(G)≤|V2|，即2γ(G)≤2|V2|=γr(G)。又由引理1 知γr(G)≤2γ(G)，故γr(G)=2γ(G)。

推论1对任意的图G= (V,E)，则γr(G) =γR(G) = 2γ(G)，当且仅当存在一个γr(G)-函数f=(V0,V1,V2)，使得V1=∅。

推论2对任意的图G=(V,E)，如果γr(G)为奇数，则图G不是弱罗马图。

定理2如果图G=(V,E)的阶数为n且包含一个度为n−1 的顶点，并且G ̸=Kn，则图G既是罗马图也是弱罗马图。

证明 由于G ̸=Kn，由引理5 可知γ(G) = 1，并且γr(G) =γR(G) = 2，故γr(G)=γR(G)=2=2γ(G)，即图G既是罗马图也是弱罗马图。

定理3设树T的强支撑点集合为SS(T)，如果γr(T) = 2γ(T)，则存在一个γr(T)-函数f=(V0,V1,V2)，使SS(T)⊆V2。

证明 由于γr(T) = 2γ(T)，由定理1 可知，存在一个γr(T)-函数f= (V0,V1,V2)，使得V1=∅。假设存在v ∈SS(T)V2，则v ∈V0。又由于v是树T的强支撑点，则至少存在两片叶子，不妨设u和w是它的叶子，则uv,wv ∈E，并且uw/∈E。因此u,w ∈V1矛盾，故SS(T)⊆V2。

定理4对任意的路Pn，只有路P3是弱罗马图。

证明 对任意的n ≥1，由引理6 知γr(Pn) =「⏋，又由引理7 知γ(Pn) =「⏋，我们有：

1) 当n= 1,2 时，γr(P1) =γr(P2) = 1,γ(P1) =γ(P2) = 1，显然γr(P1)̸=2γ(P1),γr(P2)̸=2γ(P2)，故路P1和P2不是弱罗马图；

2) 当n= 3 时，如图2 所示，其中空心圈代表V0中的点，实心圈代表V2中的点。γr(P3)=2，并且γ(P3)=1，即γr(P3)=2γ(P3)，故路P3是弱罗马图；

图2 对路P3 的构造

3) 当n ≥4 时，γr(Pn)=「⏋＜2「⏋=2γ(Pn)，故路Pn(n ≥4)不是弱罗马图。

综上，对任意的路Pn，只有路P3是弱罗马图。

定理5星K1,t(t ≥2)是弱罗马图。

证明 对于星K1,t(t ≥2)，如图3 的构造，其中空心圈代表V0中的点，实心圈代表V2中的点。显然γ(G) = 1，并且γr(G) = 2，即γr(G) = 2γ(G)，故星K1,t(t ≥2)是弱罗马图。

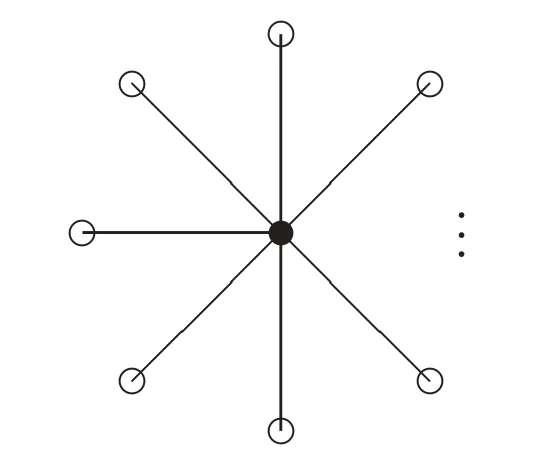
图3 对星K1,t(t ≥2)的构造

定理6设星K1,t1,K1,t2,···,K1,tn(ti ≥3,i=1,2,···,n)的中心点分别记为v1,v2,···,vn，并记vi1,vi2∈V(K1,ti)(i= 1,2,···,n)为星K1,ti(i= 1,2,···,n)的任意两个外点，则：

(a) 由中心点v1,v2,···,vn依次用边连接成一条路，所构成的树T1是弱罗马图，如图4 上图，其中空心圈代表V0中的点，实心圈代表V2中的点；

(b) 让外点vi2与vi+1,1(i= 1,2,···,n −1)用边连接，使v1,v12,v21,v2,v22,···,vn−1,2,vn1,vn成一条路，所构成的树T2是弱罗马图，如图4 下图。

证明 (a) 由于星K1,t1,K1,t2,···,K1,tn(ti ≥3,i= 1,2,···,n)的中心点分别为v1,v2,···,vn，如图4 上图的构造，则显然S={v1,v2,···,vn}是 树T1的一个γ(T1)-集，并且γ(T1) =|S| =n。令函数f= (V0,V1,V2) = (V −S,∅,S)，显然f是树T1的一个γr(T1)-函数，并且

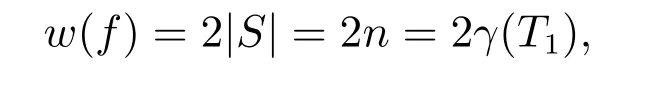
故树T1是弱罗马图。

(b) 如图4 下图的构造，显然S={v1,v2,···,vn}是树T2的一个γ(T2)-集，并且γ(T2) =|S| =n。令函数f= (V0,V1,V2) = (V −S,∅,S)，显然f是树T2的一个γr(T2)-函数，并且

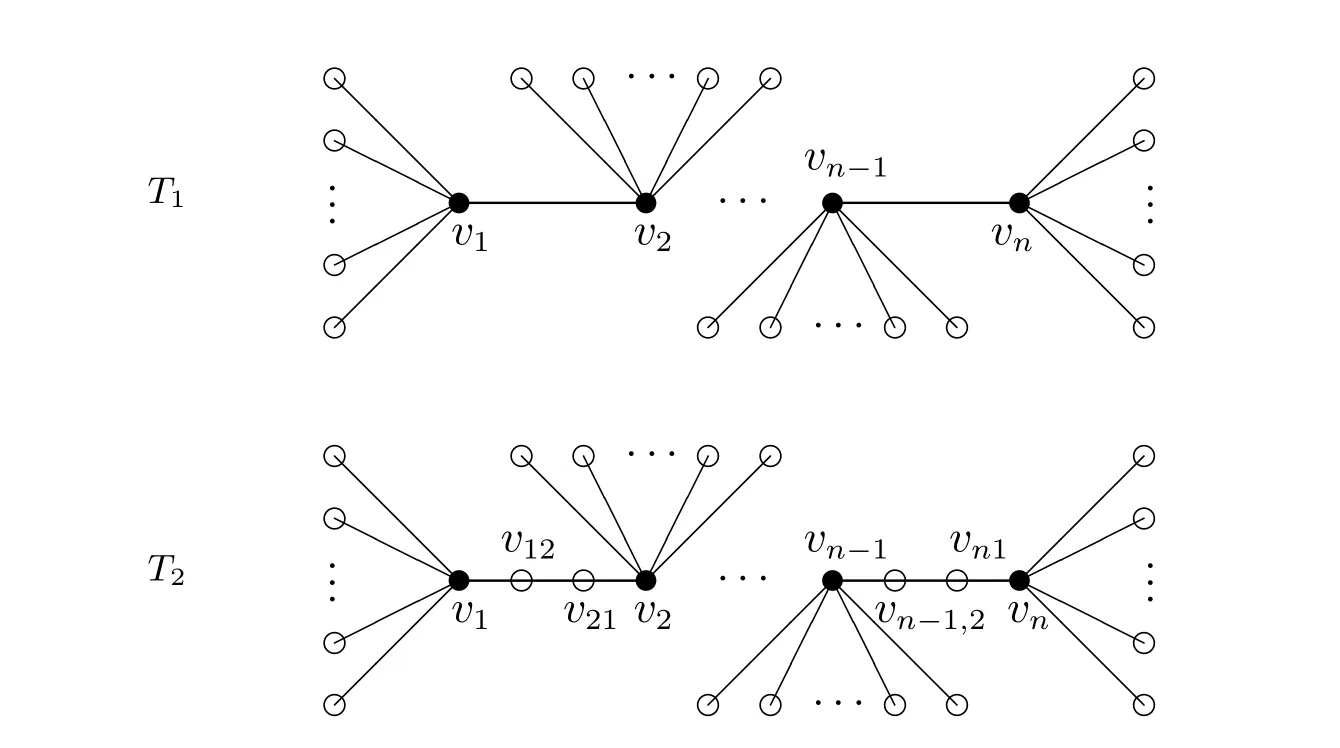
图4 对树T1 和T2 的构造

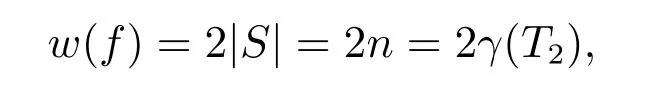
故树T2是弱罗马图。

由引理1 可知，对任意图G，γ(G)≤γr(G)≤2γ(G)，我们有下面的观察。

观察1γr(G)与2γ(G)的差距可以无限大。

例如，把星K1,t(t ≥2)的每一条边一分为二得到的图，称为细分星图，记为S(K1,t)(t ≥2)，如图5，其中图5(a)空心圈代表V0中的点，实心圈代表V1中的点，图5(b)实心圈代表控制集中的点，则由图5(a)的构造不难看出γr(S(K1,t))=t+1，而由图5(b)的构造不难看出γ(S(K1,t))=t。因此2γ(S(K1,t))−γr(S(K1,t))=t −1(t ≥2)可以无限大。

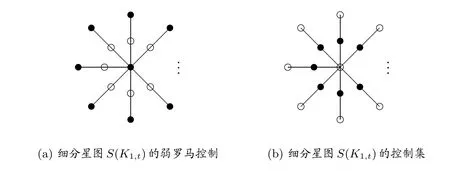
图5 对细分星图S(K1,t)(t ≥2)的构造

3 图的弱罗马控制的一些性质

在文献[3]中给出了图的弱罗马控制的一些性质，下面我们给出图的弱罗马控制的另外几个性质，对进一步研究图的弱罗马控制具有重要意义。

定理7设f=(V0,V1,V2)是图G的一个γr(G)-函数，S=V1∪V2，则：

(a) 对任意的v ∈V1，pn(v,S)构成一个团；

(b) 若存在v0∈V0,d(v0) = 2，不妨设u1,u2∈N(v0),u1v0,u2v0∈E(G)，使得u1和u2都含有至少一个S −epn，并且N[u1]−{v0}和N[u2]−{v0}构成一个团，则f(u1)̸=f(u2)。

证明 (a) 设f= (V0,V1,V2)是图G的一个γr(G)-函数。对任意的v ∈V1，设u,w∈epn(v,S)，则u,w ∈V −S=V0。因为v是S中唯一与u相邻的顶点，所以调动一个军团从v到u不会产生未防御点，即函数

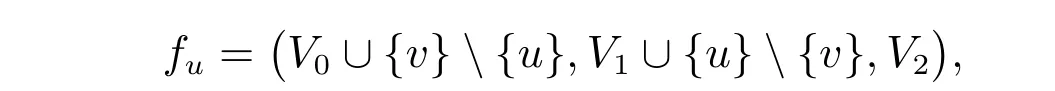
没有未防御点。但是由于N(w)∩(S−{v})=∅，则必有uw ∈E(G)。因此，epn(v,S)构成一个团，从而pn(v,S)构成一个团。

(b) 设f= (V0,V1,V2)是图G的一个γr(G)-函数。显然f(u1)和f(u2)不能同时为0。假设f(u1) =f(u2) = 1，设w ∈epn(u1,S)，由于d(v0) = 2，并且u1v0,u2v0∈E(G)。令

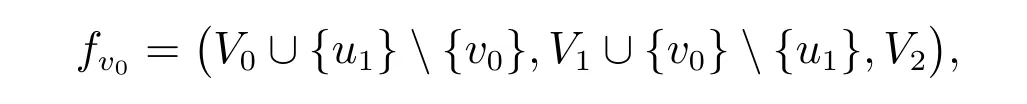
则w不与任何V1∪V2中的点相邻，因而为未防御点，与已知矛盾。若令

同理导出矛盾。假设f(u1)=f(u2)=2，令fu1=(V0,V1∪{u1},V2{u1})。由于N[u1]−{v0}构成一个团，则pn(u1,S)⊆N[u1]−{v0}，易见fu1是图G的一个WRDF。但是fu1(V)=f(V)−1，与已知矛盾。

综上可得f(u1)̸=f(u2)。

定理8设f=(V0,V1,V2)是图G的一个γr(G)-函数，则：

(a) 若u ∈V2,v ∈V1，并且uv ∈E(G)，则N(u)∩V0̸=∅；

(b) 对任意的v ∈V2,|N(v)∩V0|≥2。

证明 (a) 假设N(u)∩V0=∅，由于u ∈V2,v ∈V1，则令fu=(V0,V1∪{u},V2{u})，即fu(u) = 1 且fu(w) =f(w),∀w ∈V −{u}，则顶点u仍然能够被防御，又其他防御体系未变，且N(u)∩V0=∅，即N(u)⊆V1∪V2，故对任意的w ∈V −{u}仍然能够被防御。因此，fu没有未防御点，即fu是图G的一个WRDF。但是

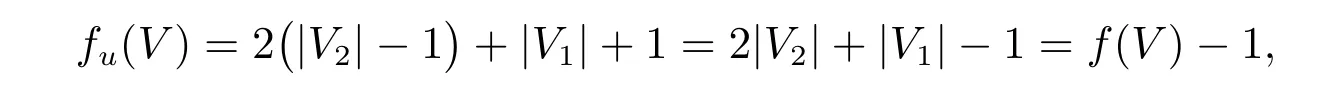
与已知矛盾，故N(u)∩V0̸=∅。

(b) 假设存在v ∈V2，使得|N(v)∩V0|≤1，即N(v)∩V0=∅或{v0}，则令fv=(V0,V1∪{v},V2{v})，即fv(v) = 1 且fv(w) =f(w),∀w ∈V −{v}，则顶点v仍然能够被防御，又其他防御体系未变，若N(v)∩V0=∅，即N(v)⊆V1∪V2，则对任意的w ∈V −{v}仍然能够被防御，若N(v)∩V0={v0}，则调动一个军团从v到v0不会产生未防御点，从而对任意的w ∈V −{v}仍然能够被防御。因此，fv没有未防御点，即fv是图G的一个WRDF。但是

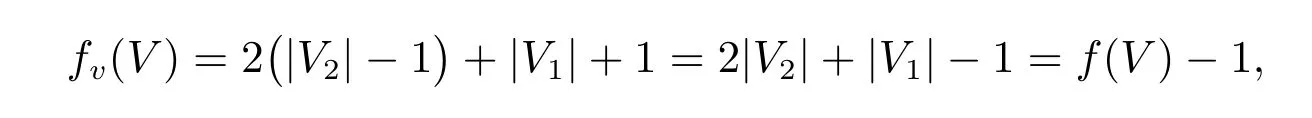
与已知矛盾，故对任意的v ∈V2,|N(v)∩V0|≥2。

注1定理8(a)中的条件u ∈V2不可减少，否则结论不一定成立。例如，设由P3=v0v1v2两端点v0和v2分别生成完全图K3所构成的图记为G，如图6，其中空心圈代表V0中的点，实心圈代表V1中的点。令

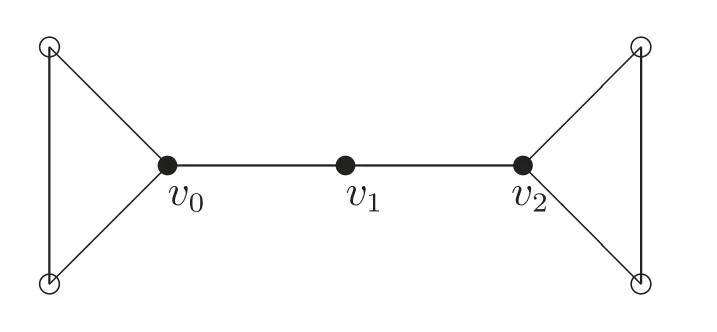
图6 对图G 的构造

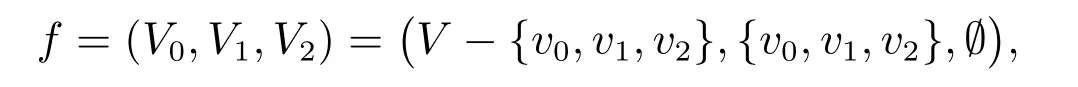
则显然f是一个γr(G)-函数，而N(v1)∩V0=∅。