基于DCC-GARCH模型对服务业板块的多元分析

钟林洲 谭 美 赵江琪 申 敏

（1.南京工业大学数理科学学院,江苏 南京 211816；2.南京审计大学政府审计学院,江苏 南京 211815）

2020年全球范围内的经济波动对我国各类服务业产生了不可小觑的影响。研究该波动对各行业的影响以及对缓解经济下行压力、稳定国民经济而言具有重要意义。首先从收益率的波动性分析，行业的波动性与行业发展稳定性关系紧密，此外由于波动聚集效应，收益率的波动性往往具有可预测性；其次能否正确描述行业间动态相关关系，会对投资组合、风险管理的正确性及有效性产生直接影响，由此来看行业间的关系更加紧密。本文对教育、酒店及餐饮、旅游三个行业作为研究对象分析其行业发展动态，选择上海证券行业板块指数作为数据依据，以此研究经济波动对服务业板块产生的影响。

1 文献综述

现代金融市场中不同行业及市场之间存在波动关系，根据波动特征对波动进行预测，并对收益率波动关联性进行分析，能够实现对多个资产组合金融头寸风险的度量，这是当下对多元波动率研究的最新发展趋势。

在对国内整体股市波动性的研究上，章楷乐等（2020）[1]基于ARMA-GARCH模型研究了经济波动下的商业银行利率波动性；董秀良等（2009）[2]、吴明毅（2013）[3]通过多元GARCH模型对国内外指数数据进行了收益率与波动相关性的实证分析，但这个模型在经济意义解释等现实方面不够明确，且存在参数过多、计算过于复杂等缺点；Engle（2002）提出了动态条件相关系数模型（DCCGARCH模型），这一模型和之前的模型相比不仅模型参数少，而且能很好地刻画多个资产之间的动态相关性，刘可等（2011）[4]、周亮（2021）等[5]也运用此模型对股票进行了相关研究。本文主要借助DCC-GARCH模型对服务业板块波动及其内部动态相关性展开分析。

2 DCC-GARCH模型理论介绍

为了避免估计模型中包含太多的滞后项，波勒斯列夫（Bollerslev）引入了一种称为广义自回归条件异方差模型（generalized autoregressive conditional heteroscedasticity）的ARCH模型的变形，也称为GARCH模型[6]。对于一个对数收益率序列rt，令为t时刻的新息。我们称服从GARCH(m,s)模型，若满足式（1）：

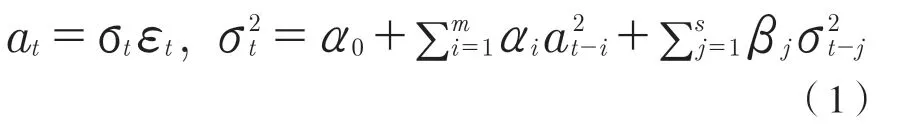
DCC-GARCH模型全称为动态条件相关模型，该模型认为相关系数是随时间变动而变动的。该研究方法包括两个步骤：第一，通过估计每个变量的单变量GARCH模型来生成标准离差；第二，使用第一步得到的标准离差来获得标准化残差，再以GARCH模型形式使用该标准化残差估计相关矩阵。

假定各资产收益率符合GARCH(1,1)模型，该模型的标准化残差将被用来估计DCC-GARCH模型的相关系数：

3 实证分析

3.1 数据的选取、处理及描述

本文以上海证券的行业板块指数为研究对象，收集2020年1月2日—2022年5月20日教育、酒店及餐饮、旅游三个行业指数日收盘价数据（数据来源于同花顺软件），对价格序列进行对数差分处理，得到三个行业指数的日对数收益率序列，并对其进行分析（将教育、酒店及餐饮、旅游三个行业分别记为education，catering，tourism）。

图1为教育、酒店及餐饮、旅游三个服务业行业的日对数收益率情况。由图1可知，每组数据在0坐标轴附近上下波动，初步判断其波动相对平稳。通过表1对教育、酒店及餐饮、旅游三个行业日对数收益率统计分布情况进行统计分析。

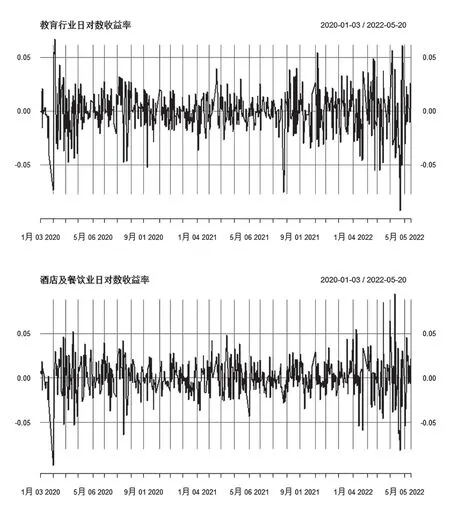
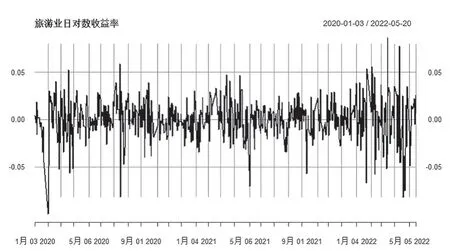
图1 三行业日对数收益率图

由表1可知，教育、酒店及餐饮、旅游三个行业日对数收益率的均值趋于0；其最小值在-0.1～-0.09之间波动，而最大值的差异较为明显；三个序列的偏度值小于0，属于左偏分布；超额峰度值大于0，具有尖峰厚尾特征。

表1 三行业日对数收益率统计分布情况

3.2 平稳性和ARCH效应检验

对时间序列的模型而言，其关键前提假设在于时间序列是否平稳，如果时间序列是非平稳的，则可能引起伪回归等问题。文章采用拓展DF单位根（Augmented Dickey-Fuller，ADF）方法对三个行业日对数收益率序列进行平稳性检验，检验结果如表2所示。

表2 ADF检验结果

ADF检验的原假设为序列存在单位根（即序列不平稳），结果显示教育业、酒店及餐饮业、旅游业的日对数收益率序列都在1%显著水平下拒绝原假设，不存在单位根，具有平稳性特征。

在三个行业日对数收益率序列具有平稳性的基础上，对其进行条件异方差检验（即ARCH效应检验）。第一个检验是将常用的Ljung-Box统计量Q（m）用于序列为t时刻的新息，该检验统计量的原假设是序列前m个间隔的ACF值为零，取m为10。第二个对条件异方差的检验是Engle（1982）的拉格朗日乘子检验，统计量为F统计量。得到检验结果如表3所示。

表3 ARCH效应检验结果

对三个行业日对数收益率序列ARCH效应检验表明，教育、酒店及餐饮、旅游行业日对数收益率序列在1%显著水平下存在ARCH效应。

综合上面的分析，三个行业的日对数收益率序列具有ARCH效应的平稳序列，且均值接近于0，同时具有尖峰厚尾的特点。因此，可以考虑GARCH模型来对各组序列进行建模分析。

3.3 基于单变量GARCH模型的行业波动率实证研究

3.3.1 GARCH模型建立及参数估计

根据上文分析，三个行业日对数收益率序列平稳，因此GARCH模型的均值方程仅由一个常数构成。由于在大多数应用中，只用到低阶的GARCH模型就可以反映多数情况下金融数据的波动特征，因此采用GARCH(1,1)模型即可达到较好的效果。运用R语言计算得到带标准正态分布新息的GARCH（1，1）模型，一般波动率方程形式如下：

3.3.2 模型检验

对所估计的三个行业日对数收益率序列模型进行模型检验。模型的检验是通过对残差进行Ljung-Box检验，即白噪声检验，原假设残差为白噪声序列，表示残差序列没有自相关性（见表4）。

由表4可判断，三个行业日对数收益率的GARCH（1，1）模型的残差序列及残差平方序列在5%显著水平下都可判定为白噪声序列，说明模型拟合效果较好。

表4 GARCH(1,1)模型残差检验

3.3.3 行业波动性分析

由图2可以发现，教育行业波动率在2020年2月出现最大值，该时期受新冠肺炎疫情的影响，线下教育机构关停，对教育行业产生较大冲击，导致其波动率骤增；2020年11月—2021年7月，波动率保持在0.01上下，其波动相对平稳；2021年8月出现波动高峰值，说明在有关政策扶持下教育行业逐渐得到平稳发展，但“双减”政策对教育行业又产生了巨大影响。2022年4月开始，教育行业波动率再次出现上升趋势，这与2022年4月沪指跌破3 000点的经济巨大波动相照应。

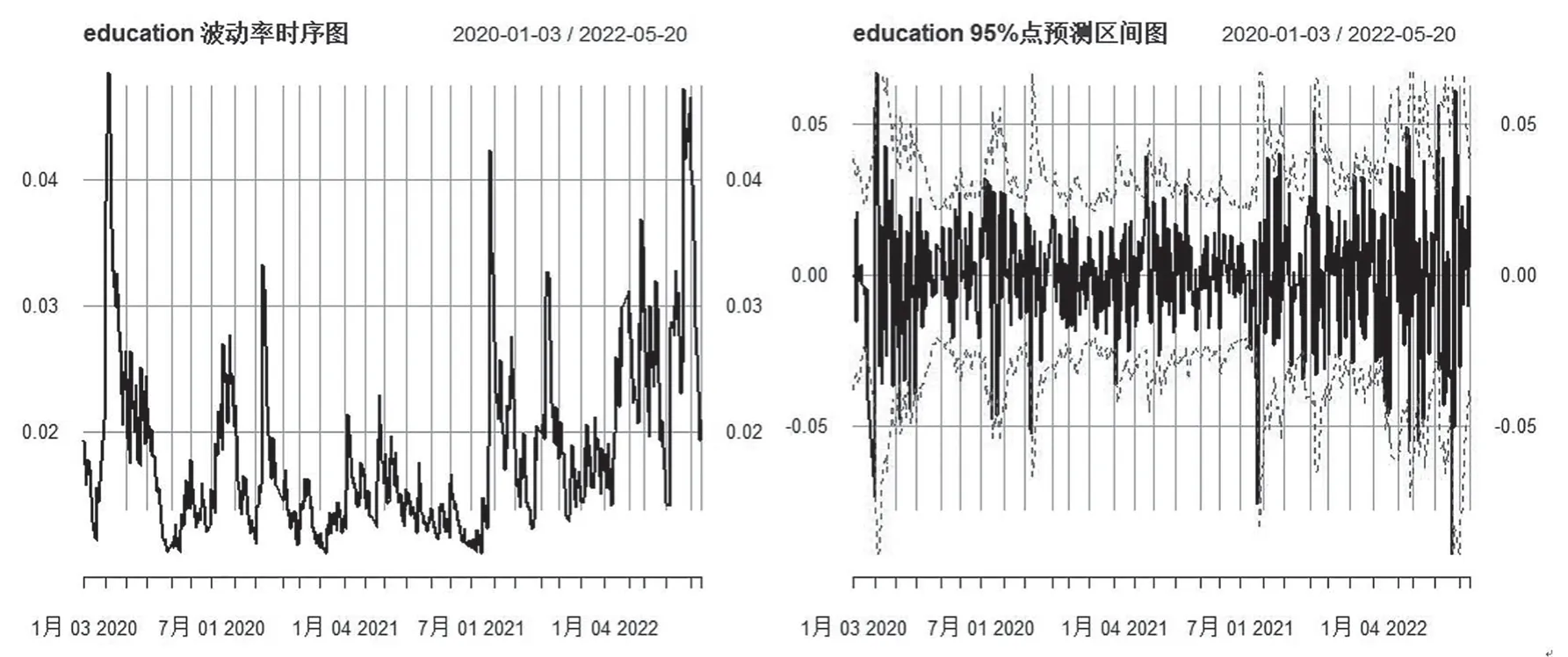
图2 教育行业波动率及GARCH（1，1）模型预测图

由图3可发现，在2020年2月和2022年3月至5月，酒店及餐饮业出现明显波动率聚集现象，和教育行业波动分析一致。不同的是，酒店及餐饮业的波动率在2021年8月并未出现上升情况。此外，2022年3月至5月，该行业波动率上升迅速，其峰值和教育行业相比更高。由此说明，经济波动对酒店及餐饮行业的影响，比对教育行业的影响更大。

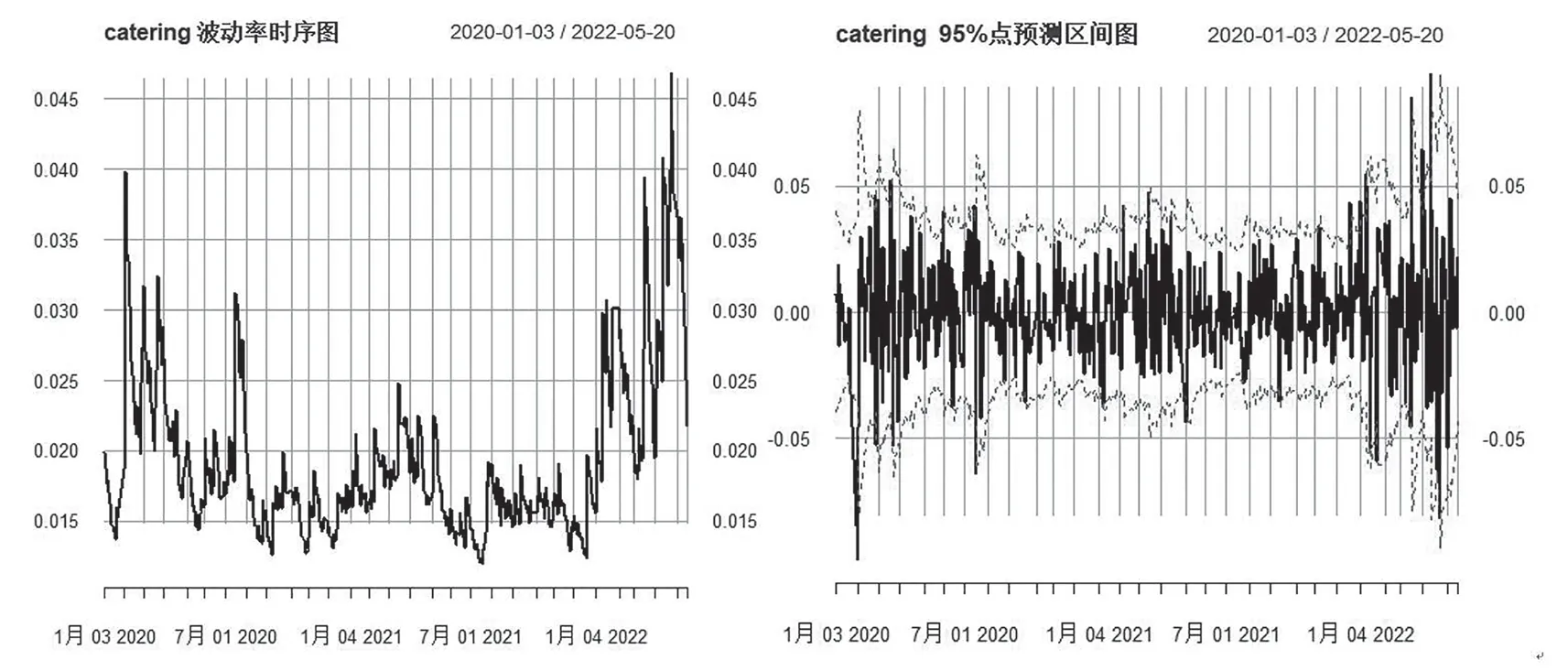
图3 酒店及餐饮业波动率及GARCH（1，1）模型预测图

由图4可知，旅游业在同时期有明显波动率聚集现象，和酒店及餐饮业有相似的趋势，说明两行业间相互传导非常迅速。与酒店及餐饮业相比，旅游业波动率从2020年2月—2022年5月出现诸多峰值，并没有长期“平稳”时期，由此说明经济波动下旅游行业发展十分不平稳。

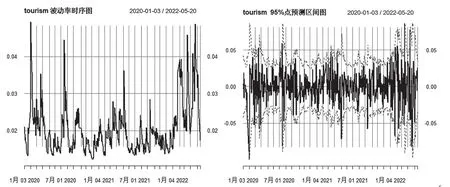
图4 旅游行业波动率及GARCH（1，1）模型预测图

3.4 基于DCC-GARCH模型的行业波动率动态相关性研究

3.4.1 序列相关性分析

采用DCC-GARCH模型，分别对三组行业的动态相关性（第一组：education和catering，第二组education和tourism，第三组catering和tourism）进行建模分析。

散点图能够直观形象地反映出序列间的相关关系，通过对数收益率序列间散点图矩阵可以大致地了解这三个行业对数收益率序列间的相关情况。由图5可发现，三个行业日对数收益率序列均表现出正相关性，尤其是酒店及餐饮和旅游业，从分布角度而言，三个序列也表现出了相似的特征。

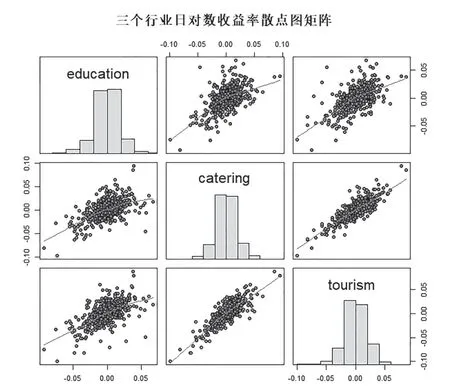
图5 散点图矩阵

3.4.2 DCC-GARCH模型的估计

根据前文分析，采用GARCH（1，1）模型对疫情后检验、酒店及餐饮、旅游行业的日对数收益率序列的波动性进行拟合，然后利用方差模型的系数作为DCC模型系数的初始值，运用R语言中的rmgarch包来估计DCC模型的系数。得到的方差方程的估计结果如表5所示。

表5中的a体现滞后一期的标准化残差乘积对动态相关系数的影响，其含义为现有信息对下一期波动性的影响力程度。由表5可知，第三组行业（catering和tourism）的a值较高，其余组的a值都较低，说明酒店及餐饮业和旅游业的行业组合对新信息的敏感度最高。

表5 DCC-GARCH模型估计系数

方差方程式中的ARCH项和GARCH项的系数之和λ=a+b，是指行业日对数收益率波动的维持性，即用来衡量现有的波动性趋势在未来消失的速度,如果λ越接近1，则表明波动性趋势在未来维持的时间越长。由表5可知，第一、二个行业组合的b大于a且两者的和有接近于1的趋势，说明教育行业对酒店及餐饮行业、教育行业对旅游业的波动的维持性都较强。总体来看，与其他行业组合相比，酒店及餐饮与旅游行业的组合对新信息的敏感度要高于其他行业组合，且在波动的维持性方面，要低于其他两个行业组合。

3.4.3 动态相关性分析

为了更加直观地分析各行业组合动态相关系数变化，根据上文的DCC模型给出疫情发生后三个行业组合的动态条件相关系数时序图（见图6）。

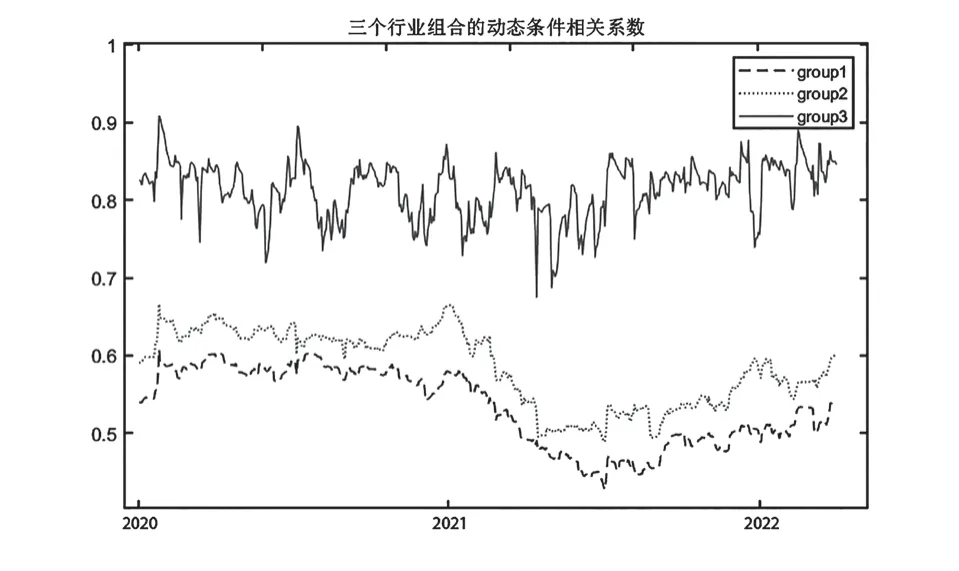
图6 动态条件相关系数时序图

由图6可以看出，第一组行业（教育和酒店及餐饮）的相关系数具有明显的趋势特征，2020年初两个行业间的相关系数较高，伴随经济波动的逐渐稳定，两个行业间相关性自2021年初下降至2021年7月达到最小值。2021年7月下旬，江苏南京、江苏扬州、湖南张家界等地的突发事件数量增加，此后两个行业间相关性再次出现上升趋势，由此说明教育行业和酒店及餐饮业波动相关性会伴随经济波动而逐渐增大；第二组行业（教育与旅游业）的波动相关性与前一组行业的情况相类似，有所区别的是，后者相关系数总体更高，且在2020年4月上升得更加明显，这与2022年4月沪指跌破3 000点的经济巨大波动相照应；而第三组行业（酒店及餐饮业与旅游业）的波动相关性要远远高于前面两个行业组合，这与这两个行业本身的属性有一定的关联。除此之外，酒店及餐饮业与旅游业的波动相关性随时间上下起伏，波动较大，但也可看出其先下降后上升的大致趋势。

4 小结

一个行业内各子行业形成了相互影响的有机系统。因此，为了分析在经济波动下我国服务业板块的经济状况，本文选取教育、酒店及餐饮、旅游三个具有代表性的行业进行多元分析。从波动性分析来看，三个行业的波动率序列在趋势走向上有明显的同步变化特征，说明三个行业之间的内在联系错综复杂、相互传导非常迅速。通过三个行业的动态相关性分析发现，行业间波动相关性随着经济波动的发生而变大，酒店及餐饮业与旅游业的波动相关性最高。根据本文的研究分析发现：

第一，行业的波动性与经济总体态势有明显的正相关关系，即波动性随产生经济波动事件的发生而变大，从行业的波动趋势可以看出，在经济冲击下，国家政府作为“有形”的手对经济调控的影响巨大，为了尽快复苏经济，应该实施对应的行业发展政策和支持政策，积极响应国家号召。

第二，行业间的动态相关系数在2020年1月—2022年5月间有一个先下降后上升的大趋势，每次相关性的变动都对应着经济波动的发生，行业间波动相关性随着经济冲击的出现而变大。

第三，行业间的动态条件相关系数具有明显的时变特征，由于波动的变化会对投资组合的风险造成一定的影响，且行业间的相关性变化会影响到避险策略。因此，观察动态相关系数的变化趋势，有助于采取合适的避险策略。