一种顾及数据时效的沉降预测模型序贯解算方法
2022-09-29郑一帆于先文董彦锋
郑一帆,于先文,董彦锋
(东南大学交通学院,江苏 南京 211189)
引言
隧道、道路、桥梁等交通构建物在工程完工后,由于土的固结效应以及其他因素变化所造成的沉降,被称为工后沉降[1]。精确预测工后沉降能够为工程的安全性评估与维护方案设计提供重要的参考。对于隧道、道路、桥梁等需要长期维护的工程项目,沉降预测的重要性更加突出。
目前,工后沉降主要通过预测模型来预测,常见的模型包括双曲线法[2]、指数曲线法[3]、星野法[4]、Asaoka法[5]、泊松曲线法[6]等。模型的参数可以通过间接平差或序贯平差的方法解算。相比于前者,序贯解算方法具有高效、节约存储的特点[7-8]。
不论何种沉降预测模型,其随机模型一般都基于观测值的精度确定。因此,现有工程普遍采用等权的随机模型。考虑到新数据比旧数据更能体现预测点的沉降变化趋势,等权的随机模型用于预测工后沉降并不合理。因此,有必要探讨新的随机模型,强化沉降预测模型的合理性,以提高沉降预测模型的预测精度。
在沉降预测模型的随机模型领域,已有一些研究及成果。殷春武[9]探讨了随机模型的一些条件,并利用了三角函数进行了观测数据的赋权,证明合理的随机模型可以改善沉降预测模型的预测效果;曹文贵等[10-11]将新鲜度的概念引进了沉降预测模型中,采用了一些新鲜度函数赋权实测观测数据,同样对预测效果有积极作用;李秋全[12]在曹的基础上,将新鲜度与吻合度结合,创造了新的随机模型应用在隧道变形预测中,取得了良好的效果。但上述的随机模型确定方法都一定程度上依赖经验,具有一定的随机性;同时,其要求明确沉降数据的总体数量用于定权,这与沉降预测模型的序贯解算方法不兼容。
针对上述问题,本文引入降权系数的概念,按时效性对实测沉降数据进行赋权,确定一种适用于沉降预测模型序贯解算方法的随机模型,以强化沉降预测模型的合理性,改善模型的预测效果,并通过工程算例验证方法的有效性。
1 沉降预测模型序贯解算方法
沉降预测模型需要伴随着工程进展而实时更新,以实时预报沉降变化情况。序贯平差理论可以高效地解算沉降预测模型,下面列出沉降预测模型完整的序贯解算方法。
大多数沉降预测模型可以表达为统一的二维线性形式,基于前m(m≥2)期数据,利用最小二乘法可拟合沉降预测模型为:
式中t为观测时间;y为包含t时刻沉降信息的因变量,为便于表达,下文直接用沉降观测量指代;为模型系数估值,等权条件下,令所有的沉降观测值的权都为1,其计算公式为:
估值的权阵为:
自m+1期起,即可利用序贯理论更新模型。下面以第n(n>m)期数据为例,导出序贯沉降预测模型计算公式。
假设基于前n-1期数据,已得到沉降预测模型的系数估值a^(n-1)及其权阵W(n-1),将其虚拟为观测值,并建立其误差阵v′(n)的方程为:
第n期新增沉降观测数据为yn,相应权为1。令Fn=[ 1f(tn)],可建立观测误差方程为:
将式(4)与式(5)联立,得误差方程式为:
式中I为二阶单位阵。
根据最小二乘法,可得当前预测模型系数的最优估值为:
相应的权阵为:
于是,更新后的沉降预测模型:
沉降预测模型序贯解算方法可以与沉降观测过程实时同步,将历史观测数据对模型的影响全部映射到预测模型的系数估值及其权阵中,节约了计算量,也可以避免历史数据存储,减小出错的概率。
2 顾及数据时效的沉降预测模型建模
2.1 建模及解算方法
目前的沉降预测模型普遍采用等精度的观测数据,并依据该精度赋权并拟合模型。换言之,沉降预测模型对所有数据的依赖性等同。而实际上,实测沉降数据距离预测时间点的时间间隔不同,其与预测时间点沉降的关联程度必定不同。时间上更接近预测点的数据,其沉降规律与预测时间点的沉降规律会更接近。所以,应当建立新的随机模型来反映数据的时效性,以获得更好的预测效果。
根据已有的沉降预测模型的数据时效性研究,可以总结出随机模型的建立原则:
(1)实测沉降数据的权是非负数。
(2)实测沉降数据的权应当呈现一个递增的趋势。
(3)沉降数据权的递增应当是一个比较平缓的过程。虽然离预测时刻点越近的沉降数据对预测值的影响越大,但相邻实测数据的权重不应差距过大,否则可能降低某些重要参考因素的影响。
假设,已基于前m期观测数据,利用最小二乘法得到预测模型系数估值a^(m)及其权阵W(m)。自m+1期起,参照上述原则,对序贯解算方法的随机模型进行改进。下面以第n(n>m)期数据为例,导出顾及数据时效的沉降预测模型序贯解算方法。
假设基于前n-1期数据,已得到沉降预测模型的系数估值及其权阵W(n-1),将其虚拟为观测值,并建立如式(4)所示的误差方程。同步引入降权系数k(0<k≤1)对虚拟观测值进行降权,得到其新的权阵为:
第n期新增沉降观测数据为yn,相应权为1,可建立如式(5)所示的观测误差方程。联合上述两组误差方程,得到形如式(6)所示的误差方程组。进而可得预测模型系数的最优估值为:
相应的权阵变为:
上述内容表述了顾及数据时效进行模型序贯解算的完整方法。方法中降权系数k的取值为随机模型保留了一定程度的灵活性,通过调整k的值,可以调节随机模型的内部结构。k的取值越接近1,算法顾及数据时效的程度越低;当k=1时,算法蜕变为常规的等权模型。相反,k的取值越接近0,算法顾及数据时效的程度越高。
2.2 数据时效性分析
随着沉降观测数据的增加,同一历史观测数据,其离预测点的时间间隔也在增加,其对预测模型所起的作用也在减小。为了分析历史沉降数据的权在量级上具体的下降规律,下面对历史观测值的权进行推导。
根据式(11),基于n期实测沉降数据进行序贯解算得到的系数估值a^(n)可写为:
将式(14)和式(15)代入式(13)中,可以得到:
式(16)分离出了包含沉降观测量yn-1的项,由此可以看出第n-1期数据的权为k。参考式(14)与式(15),可得与W′(n-2)的表达式为:
将式(17)和式(18)代入式(16)中,可以分离出包含沉降观测量yn-2的项如下所示:
由上式可得第n-2期沉降观测数据的权为k2。
重复上述过程,可分离出包含第d(m<d<n)期沉降观测量yd的项如下:
可知第d期沉降观测数据的权为kn-d。
当d≤m时,沉降观测量yd被包含在观测向量Y(m)中,利用式(2)与式(3)结果,最终可从a^(n)分离出包含Y(m)的项如下:
根据式(21)可知,此时第d期沉降观测数据的权为kn-m。
总结上述内容,第d(d≤n,n为沉降数据总量)期历史观测数据的权重为:
由于0<k≤1,根据式(22)可以看出,本文方法中同一历史观测数据的权是根据工程进展而迅速缩减的。这不仅与序贯解算方法相适应,也与工程的实际进程相适应。
3 算例验证
3.1 工程背景
本文以隧道沉降模型为例,对顾及数据时效的沉降预测模型序贯解算方法进行算例验证。实验数据选取南京市某地铁隧道内370,374,383,535号等四个沉降监测点的实测沉降数据。该组数据于2013年通过精密水准测量得到,每个沉降监测点有82期数据。
实验模型选用沉降预测模型中最常见的双曲线模型,其模型表达式为:
式中S0,t0分别为开始施工时的沉降量与时间点;α,β为根据实测值求出的系数;t,St分别为任意观测时间和对应的沉降量。
根据模型的线性方程可以进行序贯解算,获得参数估值后可进行沉降预测工作。
3.2 计算结果
为探求本算例中降权系数k取值的影响,对k取不同值进行实验,同时采用等权的随机模型进行预测作为对照。首先,选定降权系数k;其次,使用前3期数据基于最小二乘拟合沉降预测模型;然后,利用预测模型预测第4期的沉降值;接着,添加第4期的实测沉降数据基于序贯解算方法更新预测模型;进而,预测出第5期的沉降值。反复循环直到数据全部参与解算,最终得到沉降预测序列。选定不同的降权系数k,可得到不同沉降预测序列。
为了直观地分析降权系数的作用,可作沉降预测图进行辅助分析。以主体工程时间为横轴,沉降量为纵轴,绘制实测的沉降数据曲线与不同降权系数k得到的沉降预测序列制成的曲线,如图1~4所示。
从图中可以很明显地看出,顾及数据时效的随机模型可以大幅优化预测精度。对照等权情况下的预测曲线,当k值取0.9时,相应的沉降预测曲线急遽逼近实测沉降值;当k值取0.8,0.7与0.6时,沉降预测曲线与实测沉降曲线更加贴近,出现了一些重叠的部分。
为了更具体地观察k值与预测效果之间的关系,采用预测中误差作为具体的数据指标来描述预测精度。预测中误差定义如下:将实测沉降数据作为真值,利用预测得到的预测沉降序列与其作差,得到预测误差的序列。基于该序列可算得全部预测值的均方根误差作为预测中误差。根据实验结果,整理不同k值与相应的预测精度如下表。
对比表1中不同k值的预测结果,可以发现,k调整到0.9时,预测中误差较等权条件下缩小了50%左右;继续减小k的值,预测中误差的下降幅度逐渐变小;当k取0.6时,预测精度较等权情况能够提升4~8倍。
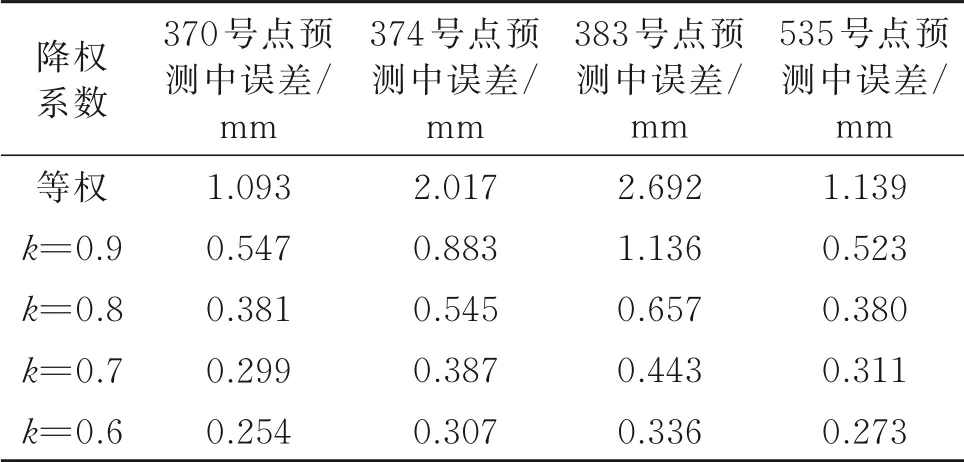
表1 不同k值的模型预测精度
由上述结果可知,在该工程中,等权条件下的沉降预测模型预测效果并不理想。引入降权系数后,模型预测中误差显著减小,模型性能最高可提升数倍。这说明本方法可以有效提升沉降预测模型的预测效果,提高沉降预测模型在实际工程应用中的可靠性。
4 结束语
本文提出了一种顾及数据时效的沉降预测模型序贯解算方法。该方法充分考虑了建模过程中历史沉降数据的时效性,引入了降权系数来优化定权方法,得到了相应的随机模型,并将其用于序贯解算方法中。同时,分析了随工程进展的历史沉降数据权的变化情况。最后,通过实际的工程算例对本文新方法进行了有效性验证。算例结果表明,通过引入降权系数k,沉降预测模型的性能得到了大幅提升,当k取0.6时,模型预测精度较等权情况能提高4~8倍,这对实际工程中的沉降处理工作具有重要意义。由于本文篇幅有限,对于降权系数k最佳取值的研究不够深入,后续还需进一步研究。
