重载散粒货物的铁路货车车体模态计算方法研究

徐 聪，刘宏友，汤劲松，李家宝，赵尚超，许钦华

(1.中车青岛四方车辆研究所有限公司，山东 青岛 266031； 2.中车齐齐哈尔车辆有限公司，黑龙江 齐齐哈尔 161002)

随着我国对货运能力需求的增长，铁路货运列车得到快速发展，其运载能力也大幅提升。其中，以敞车为主力军的货运车辆从建国初期的30 t级到20世纪五六十年代的50 t、60 t级再到如今研发生产的70 t和80 t级敞车，其总数量约占全国货运车辆的60%。C70E型通用敞车作为在中国标准轨距铁路上应用的通用型铁路货车，其主要用于装运煤炭、矿石、建材、机械设备、钢材及木材等货物。货物作为影响敞车车体动力学行为的主要因素，尤其是运输散粒货物类。因其性质介于固体和液体之间对于车体的动力学特性影响很大。散粒货物不具备固体的连续性和液体有规律的流动性，有着其独特、复杂的非线性特性。近年来许多学者对散粒货物的模拟也尝试了不同的方法，例如李立东[1]等将散体简化为无刚度的质量点附着于底架地板，于跃斌[2]、王婧[3]等采用Drucker-Prage材料模型建立三维实体模型。但各位学者均未能进行统一的对比论证，得出比较适宜的散粒货物模拟方法。本文采用基于C70E型通用敞车重载散粒货物煤炭为研究对象，旨在通过相关计算对标工作，探索散粒货物煤炭在模态计算中的模拟方法，同时，研究预应力对模态频率的影响，更好地应用于实际工程分析中。

1 基本理论

1.1 有限元模态分析

描述振动系统的动力学微分方程可表示为：

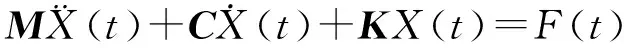
(1)

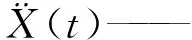
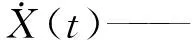
X(t)——位移向量；

M——质量矩阵；

C——阻尼矩阵；

K——刚度矩阵；

F(t)——载荷向量。

通常采用有限元求解系统的固有频率和模态振型，主要是求解结构无阻尼和自由状态下系统的动力特性方程[4]：

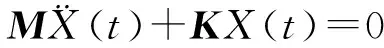
(2)

上式的解可以假设为以下形式：

X=φsinω(t-t0)

(3)

式中：φ——n阶向量；

ω——向量φ的振动频率；

t——时间变量；

t0——由初始条件确定的时间常数。

将式(3)带入式(2)可得广义特征值求解方程：

Kφ-ω2Mφ=0

(4)

求解式(4)可确定φ和ω，得到n个特征解：

其中，ω1，ω2，…，ωn代表系统的n个固有频率，且0≤ω1<ω2<…<ωn。特征向量φ1，φ2，…，φn代表系统的n个固有振型。

则系统的固有频率：

(5)

1.2 试验模态分析

对于试验模态分析，对式(1)两边进行拉普拉斯变换，得到复模态矩阵代数方程[5]：

[Ms2+Cs+K]X(s)=F(s)

(6)

获取广义导纳矩阵(即传递函数矩阵)：

H(s)=[Ms2+Cs+K]-1

(7)

令s=jω，即可得到系统在频域中的响应向量和激励向量的关系式：

X(ω)=H(ω)F(ω)

(8)

依据各阶模态之间的加权正交性，进一步得出j点激振(其余点激振为零)、i点响应时的传递函数：

(9)

其中，

(10)

(11)

式中：mr——第r阶模态质量(又称为广义质量)；

kr——模态刚度(又称为广义刚度)；

ωr——第r阶模态频率；

ξr——模态阻尼比；

φr——模态振型系数。

应用式(9)可以识别出车体的模态参数。

2 C70E型通用敞车空车模态计算

为了保证C70E型通用敞车重载模态计算时模型的准确性，需要先进行空车模态计算并与试验结果对标，验证有限元建模的准确性。

2.1 有限元模型建立

根据C70E型通用敞车设计三维模型，采用大型通用有限元建模软件HyperMesh建立了整备车辆有限元模型，单元总数约114万。C70E型通用敞车整备车辆的有限元模型如图1所示。基本材料属性见表1。

图1 C70E型通用敞车整备车辆有限元模型

表1 C70E型通用敞车基本材料参数

敞车建模时对于车体中存在的大量板材和型材结构件均采用中面壳单元进行建模；对于转向架实体结构则采用实体单元进行模拟；对于车体中存在的弧焊连接方式均采用共节点或壳单元连接的方式建模；对于心盘连接则采用刚性单元耦合模拟并释放垂向轴转动自由度；对于其他铰接连接(例如车门连接)均采用刚性单元耦合模拟同时考虑相应的自由度释放情况；对于整备车辆中涉及的橡胶簧和钢簧均采用弹簧单元进行建模并依据实际刚度设置，相关弹簧刚度如表2所示。

表2 弹簧刚度统计表 N·mm-1

2.2 车体垂向静挠度对标

在进行模态计算之前，根据车体相关静挠度试验[6]，对建立的车体有限元模型进行了初步静挠度试验对标。垂向静载荷包括车体自重和载重(考虑雨雪增载的影响，取标记载重的1.15倍为载重)，C70E型通用敞车垂向静载荷为94.9 t。

垂向静载荷工况下，中梁中央处相对于心盘处和下侧梁中央处相对枕梁端部的计算与试验静挠度值。垂向静挠度计算与试验一致性较好，车体有限元模型静刚度与实车刚度相当，因此建立的车体模型准确可靠。垂向静挠度计算与试验对比如表3所示，图2为计算静挠度云图。由表3可知：垂向静挠度计算与试验一致性较好，车体有限元模型静刚度与实车刚度相当，因此建立的车体模型准确可靠。

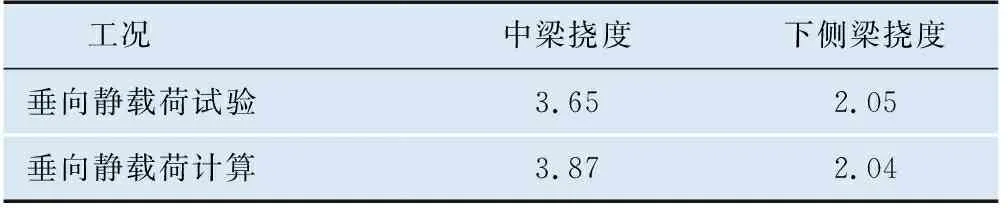
表3 垂向静挠度计算与试验对比 mm

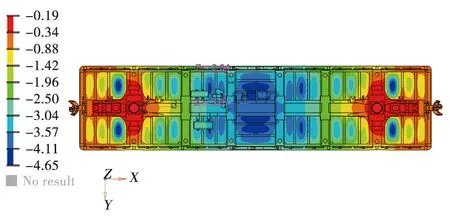
图2 垂向静挠度计算云图

2.3 空车模态计算与试验对标

空车模态计算(含转向架)约束车辆1位端轮对全部自由度，2位端轮对除行进方向的所有自由度。空车模态计算与试验[5]对比统计结果见表4。根据结果显示空车模态计算与试验的各阶频率绝对误差均在5%以内，各阶振型及频率对标一致性较好，建立的车体模型准确可靠。

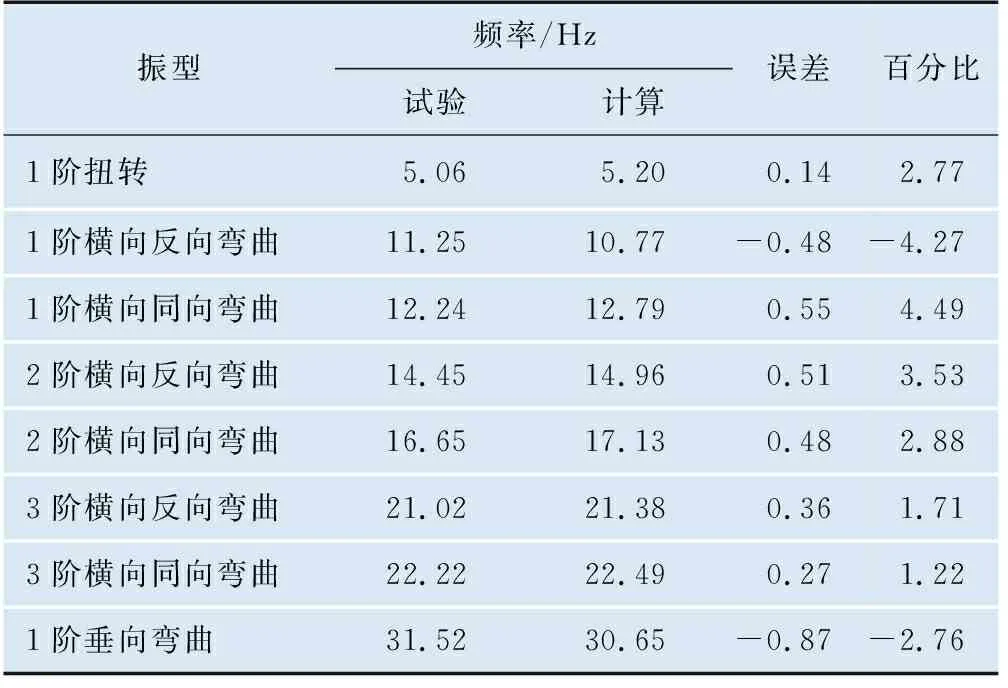
表4 空车模态计算与试验对比统计结果

3 C70E型通用敞车重车模态计算

关于C70E型通用敞车重车模态计算主要以散粒货物煤炭为研究对象，探索散粒货物煤炭相关模拟方法的适用性。散粒货物煤炭的模拟方法主要有质量点法、等效刚度模型法和Drucker-Prage材料模型法。

3.1 质量点法

质量点法是将物体通过无刚度的质量点进行简化模拟的一种方法，通常将质量点置于物体质心位置。对于C70E型通用敞车装载散粒货物煤炭而言，无法将煤炭质量集于一点，因此，通过均布质量点的方式附着于车体底架地板上。质量点法有限元模型见图3所示，重车质量点法模态计算与试验[5]对比统计结果见表5。

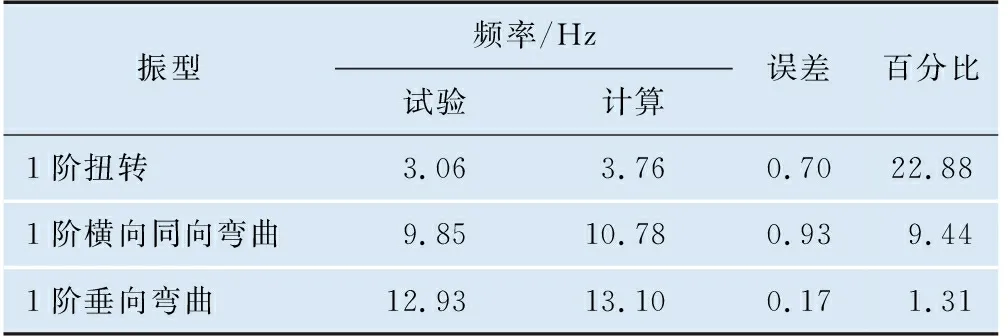
表5 重车质量点法模态计算与试验对比统计结果

图3 质量点法有限元模型

质量点法计算的车体1阶扭转模态频率误差较大，同时由于未考虑散粒货物对侧墙的影响导致1阶横向弯曲频率略高，车体1阶垂向弯曲计算精度较好。说明质量点法均布地板上无法考虑对车体扭转和横向弯曲模态的影响。

3.2 等效刚度模型法

等效刚度模型法是将散粒货物假设为弹性体并通过建立弹性体模型来等效替换原复杂的结构模型，其等效刚度一般通过试验对标获取。本节通过调整弹性体的弹性模量在5～20 MPa之间变化的计算结果与试验进行对标进而拟合出煤炭模态计算时的等效刚度。等效刚度模型法有限元模型如图4所示，表6为等效刚度模型法模态计算与试验对比统计结果，各阶模态计算的绝对误差拟合曲线如图5所示。

图4 等效刚度模型法有限元模型

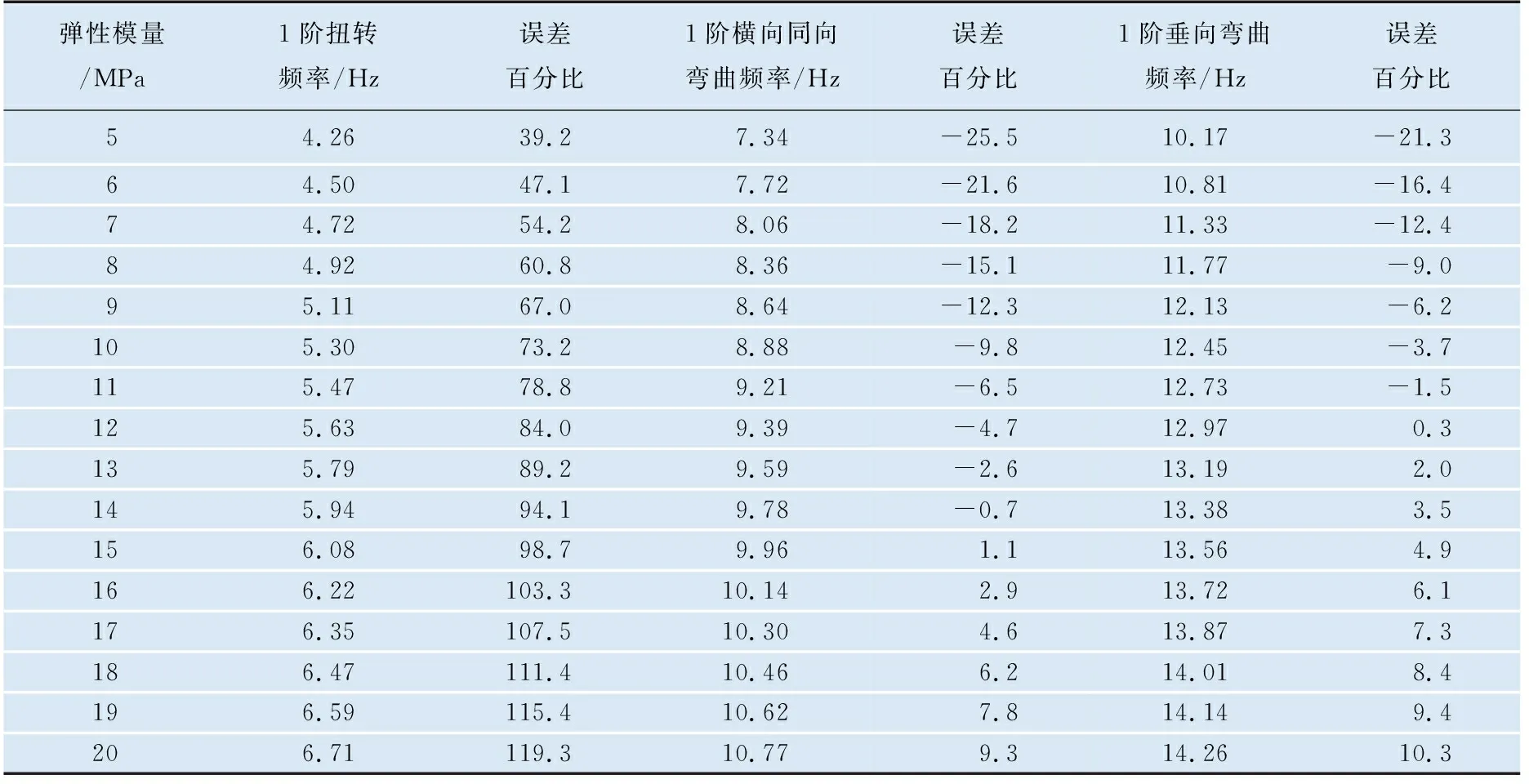
表6 等效刚度模型法模态计算与试验对比统计结果

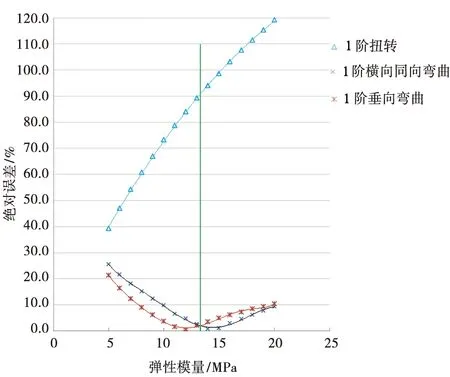
图5 绝对误差拟合曲线

等效刚度模型法模态计算能够拟合出1阶横向弯曲和1阶垂向弯曲满足计算精度的等效弹性模量(大约13 MPa)，但无法同时拟合出满足1阶扭转频率计算精度的等效弹性模量，等效刚度模型法不适用于重车全部模态振型计算。散粒货物煤炭对重车扭转刚度贡献量较小。

3.3 Drucker-Prage材料模型法

Drucker-Prage材料模型法是基于Drucker-Prage屈服准则的一种方法。采用Drucker-Prage模型能够更加准确地模拟散体的变形与受力状态，收敛性较好,目前已经在岩土力学相关分析中得到了广泛运用。本文采用Drucker-Prage材料模型进行散粒货物模态计算的同时，将同时验证2个问题：一是预应力是否对敞车车体模态计算结果存在影响；二是散粒货物建模时是否需要将散体划分成若干塑性区。

关于预应力模态分析的基本过程是在进行模态计算之前，首先进行预应力分析，然后模态计算时提取预应力分析步结束时的刚度矩阵，此时预载荷将作用于模态计算。

关于散体塑性区划分主要研究2种方式。一种是将散体划分成3块塑性区域，其主要考虑滑裂面理论和巴西果效应，对不同塑性区赋予不同的塑性参数，滑裂面倾角选取常见的60 °角(图6)，材料参数的选取见表7。第二种是将散体划分成1块塑性区域，赋予统一的塑性参数(图7)，材料参数的选取见表8。

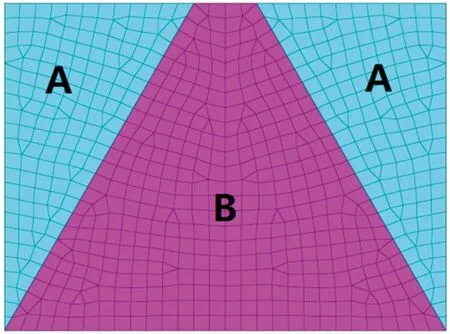
图6 Drucker-Prage模型(3块塑性区域)

图7 Drucker-Prage模型(1块塑性区域)

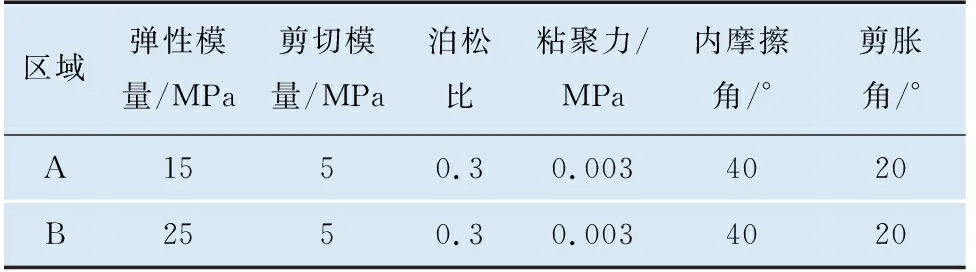
表7 材料参数(3块塑性区域)

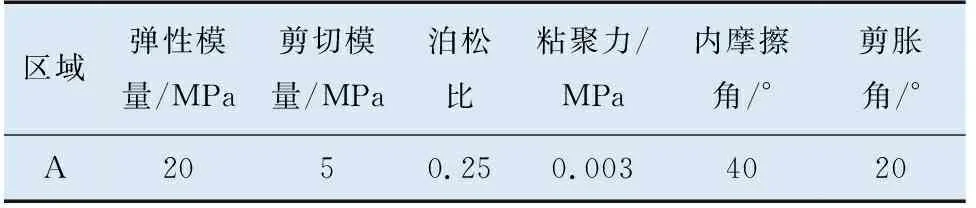
表8 煤炭材料参数[7](1块塑性区域)

采用Drucker-Prage材料模型法模态计算主要进行以下3种状态计算，无预应力货物划分成3块塑性区、施加预应力货物划分成3块塑性区和无预应力货物划分成1块塑性区域，相关计算结果与试验对比情况分别见表9、表10、表11。

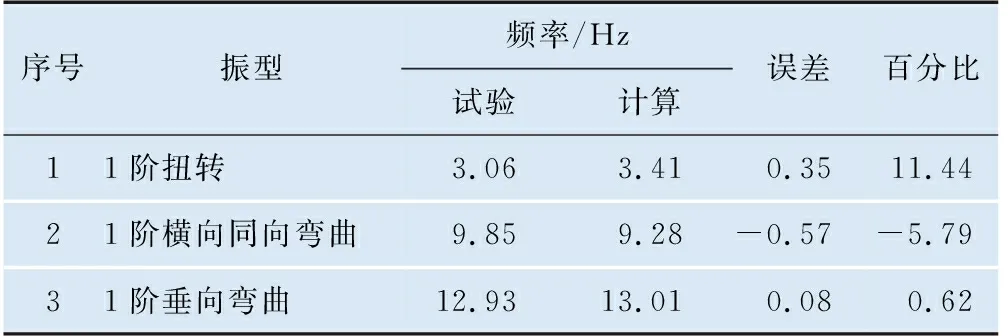
表9 无预应力货物划分成3块塑性区模态计算结果

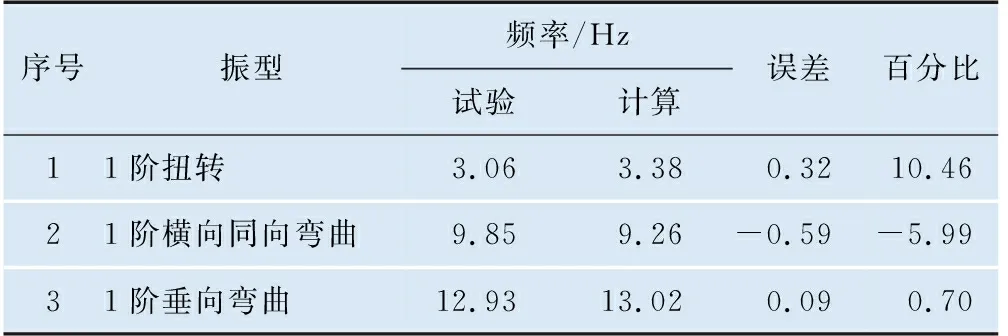
表10 施加预应力货物划分成3块塑性区模态计算结果

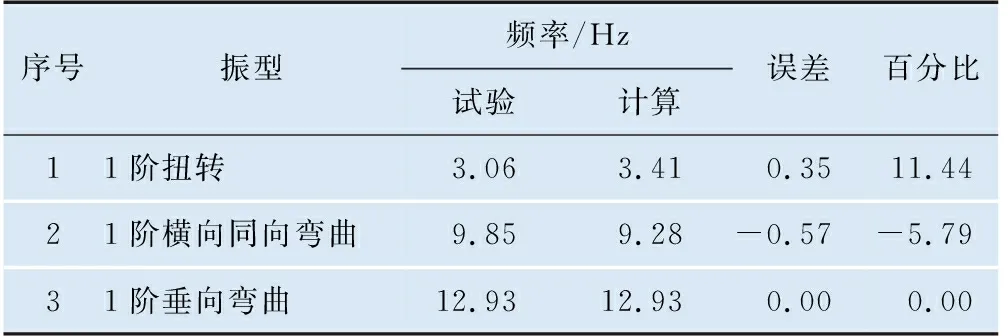
表11 无预应力货物划分成1块塑性区域模态计算结果

重车车体模态振型图，本文仅列举采用Drucker-Prage材料模型法(无预应力货物划分成1块塑性区域)计算的模态振型图和重车试验模态振型图，见图8所示。

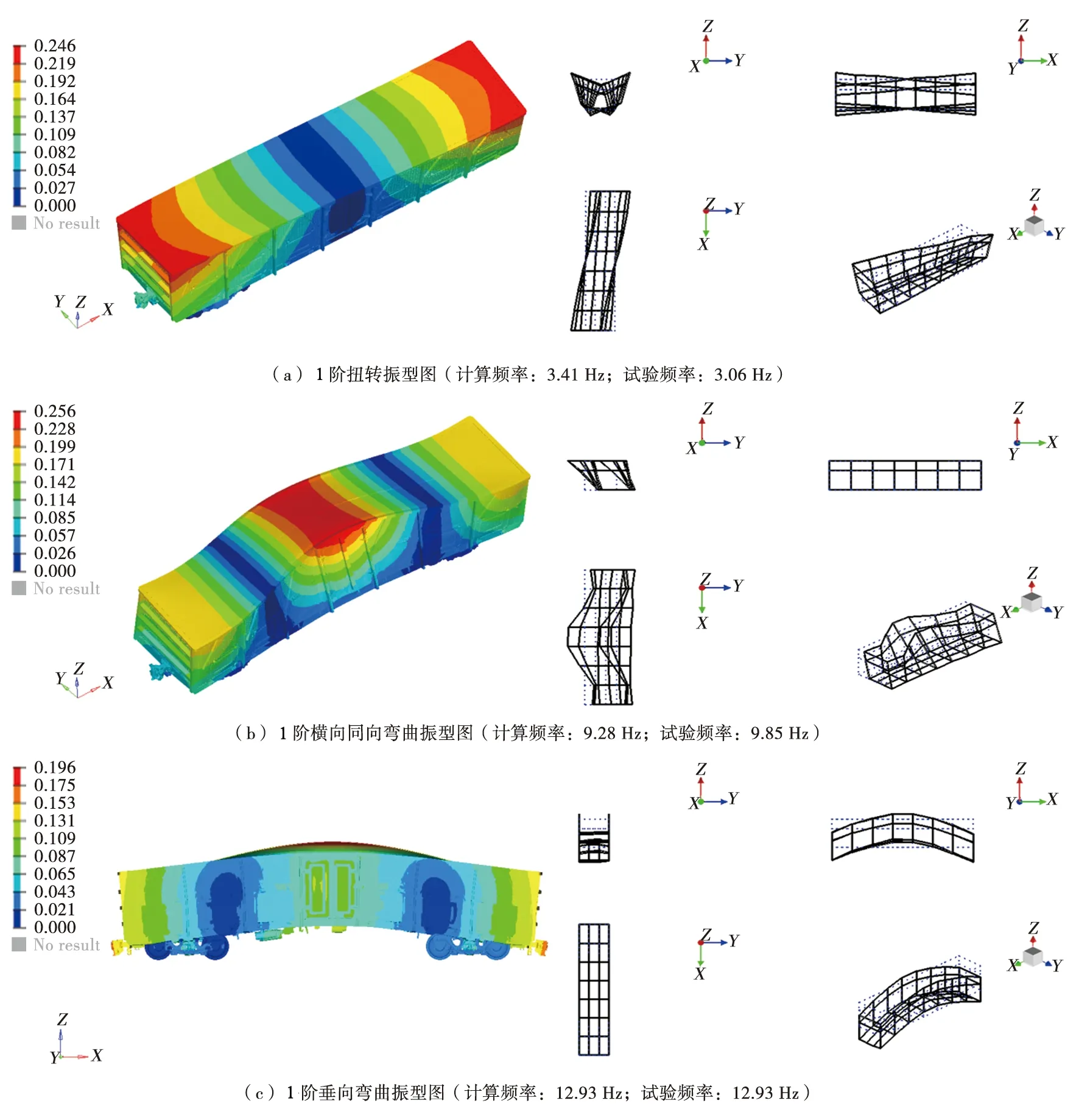
图8 重车模态计算与试验振型图

由表9、表10和表11可知预应力对敞车重车车体模态计算结果基本无影响,货物划分成3块塑性区和1块塑性区对重车车体模态计算结果无影响；采用Drucker-Prage材料模型法得到的重车各阶模态计算结果与试验一致性较好。

4 结论

通过对C70E型通用敞车有限元计算与试验对标研究，可以发现Drucker-Prage材料模型法与质量点法和等效刚度模型法相比其更适用于散粒货物煤炭的模拟，各阶模态计算结果与试验一致性较好，其计算精度能够满足工程应用需求；重载产生的预应力以及考虑滑裂面理论和巴西果效应的货物塑性分区法对重车车体模态计算结果无影响；基于敞车车辆的有限建模方法准确、可行，能够为其他型铁路货车仿真分析提供较好的指导意义。