基于交叉点复杂度的空域通行能力优化方法

马玲,刘韦廷，王航臣

(中国南方航空股份有限公司北京分公司，北京 102600)

随着中国民航地快速发展，机场建设的规模逐渐增大，机场数量逐渐增多，这导致部分繁忙的终端更加拥挤，空域资源越加紧张。以华北地区为例，北京终端是中国最繁忙的终端之一，2019年大兴机场启用后，北京空域更加紧张。在早出港的繁忙时段，为了减少延误，各航空公司时常预先调时、调减航班，这对于机场和航空公司的正常运行都是不利的。所以，对于空域通行能力的优化问题，是亟待研究解决的。

中外对于通行能力的研究主要分为终端区、扇区、航路和空域。王超等[1]提出了管制员的认知力是航路和扇区通行能力的主要限制因素，通过分析管制员的认知能力，以改进的蚁群算法为基础建立了通行能力计算方法。王莉莉等[2-3]通过图论模型对空域进行建模，讨论了危险天气、军方活动下通行能力的优化问题。王航臣[4]以动态网络流为基础，辨析了容量和通行能力的区别，并设计了一种阶段式分配流量的算法计算空域的通行能力。杨磊等[5]全面总结了空中交通流的概念、特点和建模方法。Wang等[6]为了适应日益增长的空域容量需求，以空域拥挤最小和空中交通复杂性最低为目标，提出了一种新的宏观交通分配模型，以缓解拥堵并组织空中交通流结构。赵嶷飞等[7]针对空域资源紧张的问题，从水平和垂直两个维度提出了一种终端区进场效率的评价方法，并以天津机场为例进行了验证。柯雨辰等[8]以空域的容流匹配为目标，建立了航班时刻优化模型，优化航班的滑行时间和飞行时间。Yin等[9]建立了一个多目标优化模型，旨在最小化航班延误和最大化机场通行能力，以最小间隔、时间窗口、跑道占用和航班周转为约束建立模型，并通过一种高效的多目标进化算法，利用自适应可控时间编码和目标引导个体选择两种机制，提高了计算性能。Idrissi等[10]通过优化飞机在飞行区的优化时间来解决机场通行能力低的问题，通过设计实时算法，在飞机离开停机位和接近滑行网络冲突点之前，提前检测并解决冲突。但是上述研究缺少交叉点的建模。空域的通行能力不仅受限于管制员的负荷、扇区容量，也受限于交叉点的容量。交叉点的复杂度对于通行能力有较大的影响。关于交叉点对通行能力的影响分析研究较少。

管制员负荷测量困难。现有对于管制员负荷的研究中，多借助专业设备测量获取的脑电、皮肤电等参数来衡量，使用评价方法进行计算时难以准确量化。求解算法的时间复杂度高。已有研究对于空域的刻画过于细致，而空中交通流的流动属于宏观的模型，这导致计算的时间复杂度高。通行能力的优化对于计算的时效性要求高，过长的计算时间不能满足实际运行的需求。为此，首先针对交叉点缺少建模的问题，分析了航路交叉点对于通行能力的影响，并将影响最大的交叉点流量和交叉数转化为费用函数，给出了交叉点建模的具体方法；其次，针对管制员负荷测算较为困难的问题，根据空管运行的特点，改进了网络流模型，将管制员的负荷转化为扇区容量、航路容量；最后，针对空中交通流量管理(air traffic flow management,ATFM)问题求解算法时间复杂度高的特点，提出了建模方法，并分析了延误传播的特点，以期提升通行能力。

1 问题描述

1.1 空域的抽象方法

文献[9-10]提出了使用图论的方法抽象空域计算效果好，兼顾了理论分析和实际运行。因此采用图论的方法对空域进行建模。

1.1.1 高度层的数学抽象

中国高度层的配置原则是东单西双，但国内航班常用高度层主要集中在缩小垂直间隔(reduced vertical separation minimum,RVSM)空域的下层，如飞行高度层(flight level,FL)FL291～FL321，通过简化，可以大幅降低网络的规模，从而降低计算的复杂程度，简化后的高度层如图1所示。

s表示起始航路点；t表示终止航路点起始点和终止点之间的多个高度层可以抽象为图中两个节点之间的多条边图1 简化后的高度层Fig.1 Simplified height layer

1.1.2 空域和交叉点的数学抽象

在空域的抽象方面，可以对点的集合进行简化，在计算通行能力时，一些不涉及航路改变的强制报告点和导航台点可以不进行抽象，只抽象对通行能力有影响的交叉点，这样可以大幅减小计算时矩阵的规模，降低矩阵的稀疏性，从而降低由于稀疏矩阵带来的时间复杂度。另外，以往文献对于交叉点的刻画也不够细致，交叉点inters主要分为三交叉航路点(如交叉点OC)、四交叉航路点(如交叉点VAGBI)、五交叉航路点(如交叉点SQ)、六交叉航路点4种。需要考虑交叉数对通行能力的影响。

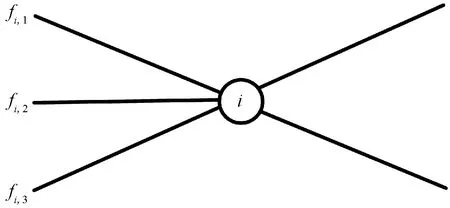
fi,1表示经过交叉点的第1股流量fi,2和fi,3分别表示第2股和第3股流量图2 五交叉航路点的抽象图Fig.2 Abstract illustration of five crossing waypoints

1.1.3 空域航班运行的数学抽象

在计算通行能力时考虑交叉点，原因在于：无论是在网络流理论中，还是实际运行中，交叉点的通行能力都容易成为网络通行能力的瓶颈。在实际运行中，由于交叉点处运行情况复杂，管制员需要花费更多的经历调配冲突，在出现流量限制时，大多以重要交叉点中心进行限制。

空管发布的流量限制分为两种：一是发布距离间隔，这是空管部门较为关注；二是发布时间间隔，这是航空公司运行控制部门较为关注的。以2021年9月15日北京区域发布的流控信息为例。距离流控：北京时12:20—15:00 经UGOTU 西安管制区不含以远高低合算 60 km一架。时间间隔流控：北京时15:30—19:00 北京/首都、北京大兴起飞经ESMEB、REVKU 珠海/金湾,深圳/宝安落地40分钟2架,最小间隔10 min。这两种流控方式都是以交叉点为核心进行流量控制的，所以空域的通行能力常常受制于交叉点。

(1)

(2)

式(2)中：T为空管的时刻间隔，取60 min；Interv，t为t时刻航班的时间间隔。如流控10 min一架，则Interv，t=10。

计算可得北京两场在北京时15:30—19:00飞往珠海、深圳的航线容量为21架次。如果时段超容就需要调时、延误甚至取消航班。

1.2 交叉点的费用函数

已有研究多在构建航路的费用函数[8-10]，但对于通行能力影响最大的因素是管制员的负荷(即空中交通流量)、交叉点的构型和扇区的容量。所以使用航路阻抗作为整个网络配流的依据，不够合理，以交叉点的结构作为费用来进行配流。

计算通行能力时需要考虑管制员的负荷，在运行中管制员负荷最直观的表现是空中交通流量，因此在设计交叉点的费用时，需要考虑空中交通流量。链接交叉点边的数量也对交叉点的复杂度有重要影响。综上所述，交叉点费用函数表示为

(3)

在正常运行的情况下，航班按照领航计划报申请的航路飞行，一般不会改航，只有在出现流量限制时，才可能出现航路航线的变更。即只有在流量控制或通行能力下降时节点的费用函数才有意义。这样设置，可以在算法迭代时只更新流控影响航路的费用函数，从而可以大大减小运算规模，降低算法的复杂度。

2 通行能力优化模型

2.1 目标函数的设置

关于通行能力的研究，目标函数一般设定为均衡各时段流量、最小化延误(网络费用)、最大化网络的流量3种。由于通行能力这一概念形成的初衷在于减小延误，科学指导航空公司调时、调减航班，所以通行能力的优化模型类似于最小费用最大流模型，即在整个网络交叉点复杂度最小的同时，网络的流量可以达到最大。但两者又有所不同，最小费用最大流问题中，使用的是边的费用，且费用固定。而通行能力的计算中，使用的是点的费用，由于流量不同，所以交叉点的复杂度是不断变化的。综上所述，目标函数可以定义为

(4)

式(4)中：D为交叉点的复杂度。

2.2 约束条件

建立的通行能力优化模型属于最小费用最大流模型的改进模型，所以首先需要满足最小费用最大流模型的约束。除此之外，还需要满足针对通行能力的改进。

2.2.1 流量平衡条件

流量平衡条件属于最小费用最大流模型中的约束，即流出量等于流入量，具体表示为对于非起飞机场和目的机场的任意两个航路交叉点∀i,j∈V，有

(5)

式(5)中：fij为由航路点i至航路点j的流量；fji为由航路点j至航路点i的流量；V为航路点的集合。

对于起飞机场s，有

(6)

式(6)中：fsj为由起飞机场s至航路点j的流量；fjs为由航路点j至起飞机场s的流量；v(f)为网络中的可行流，由网络流理论可知，可行流是一定存在的[9]。

对于目的机场p，有

(7)

式(7)中：fpj为由目的机场p至航路点j的流量；fjp为由航路点j至目的机场p的流量。

2.2.2 空域容量约束

空中交通网络与地面网络不同，地面网络在建模时可以直接套用最小费用最大流中的容量约束，即边的容量。但空中交通网络由于航路航线是一种抽象的规划，是为飞行员的飞行航迹提供引导的参考。空中交通的容量不仅受到航路容量的约束，更多的受制于管制员的负荷、扇区容量和交叉点的容量。由于在建模时，将管制员的负荷和交叉点的容量转化为了费用函数，所以在模型的约束方面，只需要考虑扇区和航路的容量约束即可，可表示为

(8)

2.2.3 流控容量约束

民航运行时，签派员会预先制作飞行计划，飞机按照规定的航路飞行，一般不会改变航路。但在出现流控时，通过更改航路，可以达到优化通行能力的目的。但在改航时，航路点i至航路点j的容量Cij不能大于流控给出的容量约束，即不能大于时刻约束下的航路容量和间隔约束下的航路容量，可表述为式(9)和式(10)。

(9)

(10)

2.2.4 整数和非负约束

分配的交通流量需要满足整数和非负约束，即向空中交通网络中分配的交通流量必须为整数，且不能出现负流量。以f表示交通流量，Z+表示正整数的集合，整数与非负约束可表示为

f∈Z+

(11)

3 求解算法设计

3.1 空中交通网络延误的反向传播特性

在设计算法之前，需要了解在出现流量控制时，空中交通网络延误的传播特性。在出现流量控制或禁航时，会导致部分航路通行能力下降甚至不可使用。这种下降会导致航路网络结构上产生拥堵，从而导致通行能力的大幅下降。以中国民航局发布的航行资料汇编(aeronautical information publication,AIP)2017-Nr.13中航路图部分(enroute chart,ERC)的ERC3兰州情报区的部分航图为例，如图3所示。W66航路是常发生限制和禁航的航路，取由西向东运行的3条航路：NUKTI-W66-GOVSA-W66-JNQ-W66-GOBIN-W66-DKO、NUKTI-W66-GOVSA-W66-JNQ-B330-YBL-A596-DKO、NUKTI-V67(假设临时航路开放)-CHW-V67-YBL-A596-DKO。这3条航路的范围中，强制报告点NUKTI和GOBIN，VOR/DME合装台YBL和DKO都是交叉点。根据1.1节中的抽象方法，强制报告点ATBUG、GUVSA(仅从上述3条航路来看，下同)，VOR/DME合装台CHW可以在抽象为图时忽略。

对图3进行抽象前，先定义如下概念。

定义1容差是指某一顶点流入量与流出量的差值，差值为正时是正容差，差值为负时为负容差，即

(12)

定义2负容差网络是指所有节点的最大流入量均大于最大流出量的网络。

按照定义1中的空域抽象准则对图3进行抽象，只取单一高度层进行说明，抽象后的网络图如图4所示。边旁边的数字为航路的容量，单位架次，节点名称旁的数字是容差。根据ICAO的规定，航空器至少间隔5 nm，NUKTI-GOBIN的距离为345 nm，计算可得其航路容量为69架次(不考虑扇区容量约束和管制员负荷约束，仅用作说明)，其他边同理。显然，所选部分的空域是一个负容差网络。如果航路由东向西运行，就是一个正容差网络。

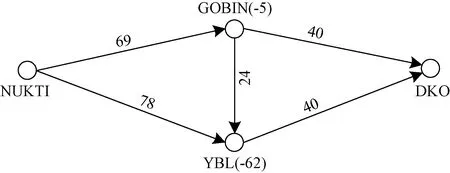
YBL为雅布赖；DKO为磴口；其他字母为航路点的五字代码图4 抽象后的负容差网络Fig.4 Negative tolerance network after abstraction

当GOBIN-DKO发布流量限制时，会导致该段容量减小，从而使GOBIN点的负容差进一步增大，导致网络延误的出现，进一步会影响NUKTI-GOBIN的容量，导致再往前流入NUKTI的流量也受到限制。

由此可知，流控可能导致网络中出现甚至增大负容差，导致通行能力下降以及延误，并且这种延误不会向后传播，而是向前传播影响之前的交叉点。因此，空中交通网络的延误传播具有反向传播的特征，需要设计一种能够考虑反向传播的算法来优化通行能力。

3.2 考虑延误反向传播的通行能力优化算法

在正常运行的情况下，飞机的计划航线是固定的，根据领航计划报申请的航路执行。在出现流量控制时，会出现延误反向传播现象，此时就需要根据流控信息的限制进行配流，适当改变飞机的计划航路，从而达到优化通行能力的目的。

步骤2计算网络容差φ。根据流控信息更新航路容量Cij，根据更新后的容量向前计算网络的容差φ。

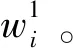
步骤4配流。以小时作为时间窗，调用最短路算法向网络配流fnum，num=num+1。

步骤5更新费用函数。根据网络中的流量，更新费用函数。

步骤6容量检验。网络中分配的流量需满足模型中的容量约束[式(9)、式(10)]。如果fij≥Cij，则wi=+∞，剩余流量fij-Cij进入下一次迭代，转步骤3。

4 算例分析

以华北区域空域为例。2019年大兴机场投入使用后，为了优化流量分布，空域结构进行了较大调整。但即使如此，在早出港时期，由于流量过大，为了避免延误，首都、大兴两场也经常要求航空公司调时、调减航班，具体原理如图5所示。航班由于某种原因造成容流不匹配导致延误，此时航班的预计离场时间(scheduled time of departure,STD)要向后推迟，机场所有航班的撤轮挡时间(calculated off block time,COBT)也都需要向后推迟，如果能取消其中一班，其他航班COBT时间都能提前，从而保障STD正常。

图5 航班调时、调减规则Fig.5 Flight time adjustment and reduction rules

这种调整虽然可以减少后续航班的延误，但如果在出现流量控制时，通过合理的流量分配，减少航班的调时和调减，更有利于机场、航空公司和乘客。

4.1 算例空域特点分析

华北空域的主要管制交接点有APOGO、UGOTU、KAKAT、P240、ESMEB、ONAPI和ANRAT。但这些点涉及的方向不同，其中APOGO是B215航路西北方向的交接点，主要涉及银川、兰州、西宁、南线(阿克苏、库尔勒、喀什、乌鲁木齐)的航班；UGOTU是B215、W43航路西南方向的交接点，主要涉及西安、成都、重庆、昆明、大理、贵阳等的航班；KAKAT是东北、北美方向的交接点，主要涉及长春、沈阳、哈尔滨、鞍山等地的航班。由于篇幅原因，其余节点方向不再赘述。综上可知，流控限制是针对某一个方向的限制，很少有针对全方向的限制，所以在优化通行能力时，应该分方向进行优化。取北京大兴国际机场几个出港关键点一周的数据进行仿真，综合后，每个节点通过量如图6所示。

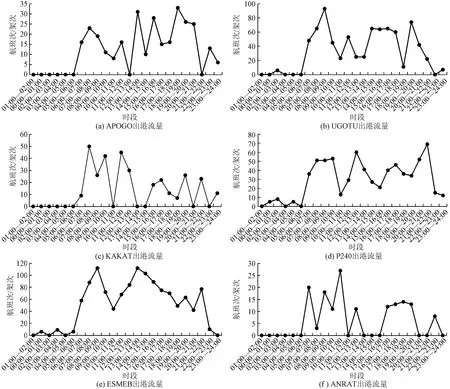
图6 大兴机场主要出港点平均航班量Fig.6 Average flight volume of major departure points at Daxing Airport

由图6可知，可能产生拥挤的时段主要是北京时间06:00—12:00(后简称时段1)，北京时间13:00—19:00(后简称时段2)两个时间段。主要对这两个时间段进行仿真。

4.2 算例仿真

4.2.1 不同流控等级下延误时间的优化结果

西安管制区在出现军事活动和恶劣天气生成时常常发布流量控制限制UGOTU的流量，会影响北京首都机场/北京大兴机场起飞经ESMEB的航班，从而产生延误。ESMEB是北京飞往广深的重要节点。以这一节点的流控为例。各种流控等级下的计算结果如图7所示。其中，优化前是指按照原航班时刻执行，优化后是指按照所提模型和算法计算，实施改航、调时、调减后的执行情况。在计算平均延误时，优化前以机场的计划航班数为除数，优化后以经过调整后的航班数为除数。在优化前后做对比时，由于需要衡量优化后比起优化前的效果，所以具体的计算方式为各时段(时段1、时段2)优化后的总航班平均延误时间的同比。

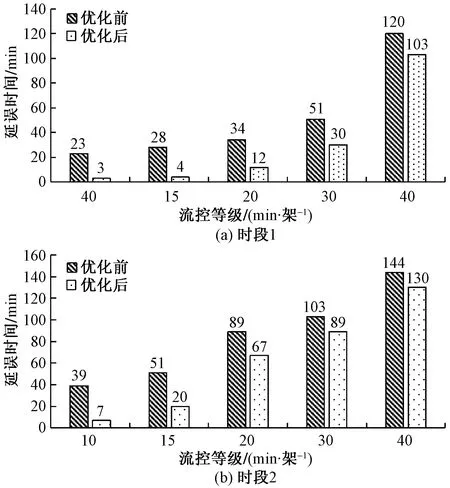
图7 不同流控等级下的优化效果Fig.7 Optimization effect under different flow control registrations

由图7可知，模型和算法可以取得较好的优化效果。京-广深线这种流量较大的航线，在流控等级较小时，可以将延误平均时间控制在10 min以内，达到消除延误的效果(规定10 min以内不算延误)，再出现较大的流控时，通过适当的改航，可以达到减小延误时间的效果，经计算，优化后比起优化前平均延误时间减小33.58%。

4.2.2 不同流控等级下受影响航班梳理的优化结果

改航、调时、调减都属于对航班的影响，但影响的效果存在差异。如通过改航避免延误，对航班的影响最小；其次是调时，调时对航空公司正常运行与旅客出行有一定影响；影响最大的是调减，调减航班航空公司需要签转旅客，甚至给予旅客一定的赔偿，对航空公司的收益和旅客的出行影响最大。通过上文的优化，以时段1，限制为20 min/架为例，改航、调时的航班如表1所示。

表1 改航、调时、调减航班的计算结果(20 min/架)Table 1 Calculation results of flight changes,time adjustments,and flight reductions(20 min/aircraft)

其他计算方法类似，限于篇幅不再赘述。将所有计算结果汇总后，对航班的影响情况如表2所示。

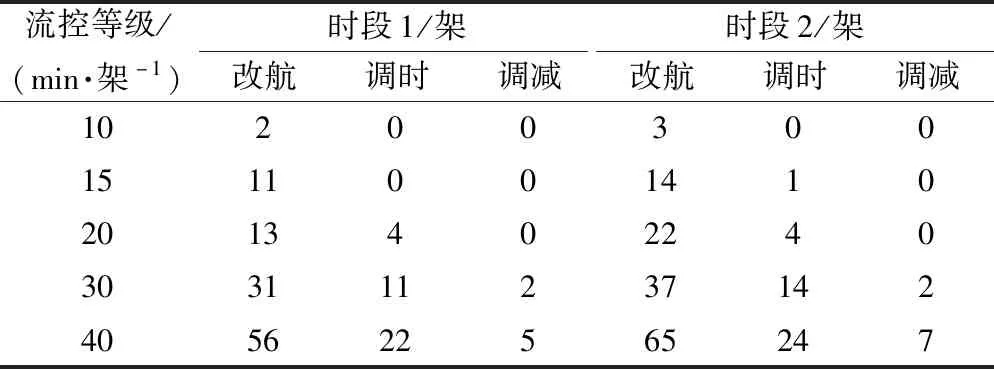
表2 改航、调时、调减航班的计算结果Table 2 Calculation results of flight changes,time adjustments,and flight reductions

通过模型优化，大多数航班通过改航来降低延误，随着延误等级的加大，才会逐渐出现调时、调减的航班，这说明模型在出现流控时能够有效地处理延误。

4.2.3 算法复杂度对比

算法的测试环境为Intel i7-6700，计算软件为Python3.7的Numpy和Networkx库。在各种流量条件下的计算时间如表3所示。

表3 算法的计算时间Table 2 Algorithm calculation time

由此可见，在高流量等级下模型的运算时间也能够满足空管的实际运行。

5 结论

考虑空管实际运行的特点，构建了交叉点的费用函数，并以延误最小作为优化目标，通过流量平衡约束、空域容量约束、流控流量约束建立通行能力的优化模型。并根据延误传播的特点建立了一种考虑延误反向传播的迭代求解算法。最后从不同的流控等级下的延误时间、受影响航班数量和算法的复杂度3个方面运行进行了仿真。得出以下结论。

(1)所提模型和所提算法在流控较小时可以有效降低延误。随着流控的增大，所提模型和算法也能有效地处理改航、调时和调减的比例关系。

(2)所提算法的时间复杂度能够很好地满足流控出现时航班的调配。