黄渤海风浪模拟波高极值在预报服务中的应用
2022-09-28孙倩倩孙颜薇
孙倩倩 王 迪 孙颜薇
(山东省威海市气象局,山东 威海 264200)
1 概述
黄渤海是山东半岛航线的主要分布区域,也是专业气象服务的重要部分。此区域中来往船只较多,因大风引起的灾害性海浪会给船舶交通运输造成巨大的经济损失和人员伤亡。同时,对于船舶航行停泊和装卸作业情况,需要对未来一段时间的波浪参数有确切的掌握,才能保证沿海作业的安全稳定运行,而波高极值是波浪参数中最为重要的资料。
目前获得一定区域内长期波浪数据的方法有很多,除了直接使用NOAA 浮标测量数据的方法外,还可以通过观测船、卫星高度计、根据风场数据模拟方法。其中,利用波浪模型再现历史波高这种研究方法在波候分析研究中应用广泛,可以得到任何有风场数据的水域内连续长期的波高数据,比较主流的模型有WAMC4、WW3、SWAN,根据前人的研究可见,WAMC4 和WW3 模型多用于计算深水情况,而SWAN对于近岸波浪的模拟较好。[1]
黄渤海地区现有的测站多位于沿岸,不能完全表示出整个黄渤海海域地区的长期波浪分布情况,因此采用第三代近岸波浪模型SWAN 模拟追算长期波浪,赵嘉静等人通过对比评选发现,在中国海域地区,使用欧洲天气预报中心(ECMWF)风场模拟的极端波情况更接近真实值,因此本文SWAN 模拟的风场来源也使用了ECMWF 风场。
本文的研究目的在于,通过ECMWF 风场数据,利用SWAN 数值模型,实现黄渤海海域波高的模拟再现,并与现有海岸上实测波高的验证,论述黄渤海海域根据实时或者预报风场资料进行波高预测的可行性。最后根据波高模拟结果,利用Gumbel 型分布函数Person Ⅲ型分布函数来进行极端波高的预测预报,为后续与波高有关的工程建设、民商互动和船舶作业提供参考决策。
2 波高模拟及验证
2.1 模型与验证
为了预测黄渤海海域波高情况,利用欧洲天气预报中心(ECMWF)风场数据驱动模型,该中心于1979年首次做出了实时的天气预报,其使用的模式充分利用四维同化资料,可提供全球在65 公里高度内60 层的40公里网格密度共两千万个点的风、气温、湿度预报。借此我们使用了2017-2019 年风场数据,数据间隔为6小时。使用第三代近岸波浪模型(SWAN)模拟了3 年中每小时波高,计算区域位于中国黄渤海,经度范围117°E-123°E,纬度范围35°N-41°N,地形水深数据来源于海图的实测精确数据。计算网格为三角形网格,共计15369 个,最大精度为0.5km 考虑了包括白盖、破波、底摩擦在内的波能耗散机制,波浪高度和波浪周期具有更高精确度。
为证明模拟结果的可信性,与国家海洋信息中心联系,取得了成山头测站(122.69°E,37.38°N)的2017 年2-4 月、2018 年2-4 月、2019 年2-4 月的实测波高数据,与模拟结果进行对比,除了实测数据有缺失的部分,模拟波高和实测数据拟合较好。为了量化模拟性能,结合了两者的相关性分析,相关系数(R)为0.81,均方根误差(RMSE)也较小,说明SWAN 模型能够较准确地模拟本地区波高的时间变化。
2.2 Gumbel 波高极值分布
Gumbel 分布的基本方法为:对于一系列的k 个随机变量(如波高值),其原始分布函数为G(x),如果在同一条件下(如黄渤海地区的气象要素),作n 次取样,能得到n 组随机变量,每组变量的最大项便可以组成一个波高极值分布。最大项的极值分布函数F(x)和原始分布函数的关系为:

其中,原始分布G(x)为指数分布,近似写作:

当变量数充分大,即k 趋近于∞时,式子(1)变为:
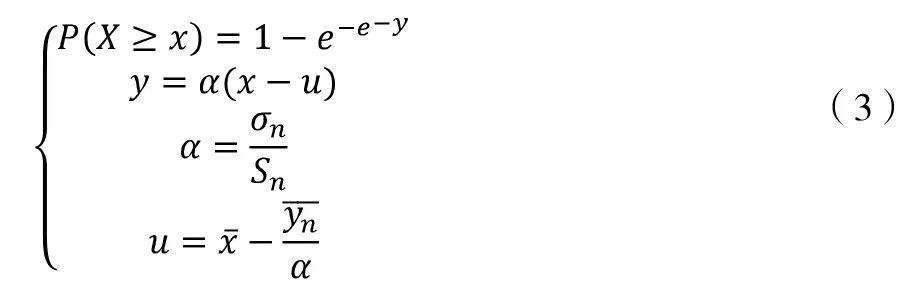
其中,Sn为样本标准差,σn和yn与累积频率P 有关,是项目n 的函数,所以当n 确定后,由P=m/(n+1)可以求得σn和yn的值,m 为k 个变量按照递减次序排列的序号,最后可以求得对于一定重现期频率的P,其对应的重现波高xp为:

根据上述Gumbel 分布的方法,对于波高模拟值结果,选择了成山头测站位置点处连续31 天的数据进行极值分析,得到的波高极值分布如图1 所示,黑色点表示的是波高模拟结果,蓝色曲线表示了根据Gumbel分布函数得到的预测曲线,两条线的拟合程度的相关系数(R)为0.79,均方根误差(RMSE)为0.21,表明Gumbel 分布对于本地波高极大值的拟合程度较好,可以作为预测预报的参考。需要注意的是,图中表示的是某一预测时间段内的波高预测值得最大值,例如:x 轴上预测天数为100 天表示的是未来100 天内出现的最大波高值约为1.59m,是一个统计概念,而并非指未来第100 天的波高值为1.59m。[2]
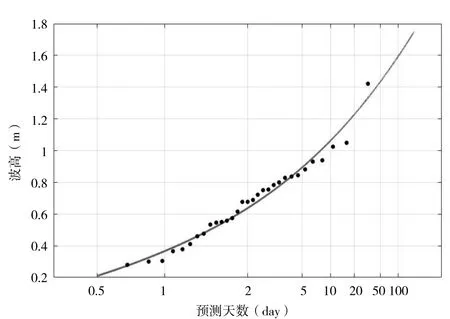
图1 模拟波高与Gumbel 分布拟合结果
2.3 Person Ⅲ型波高极值分布
Person Ⅲ型分布最初由英国K·Person 在生物学统计分析中提出,他发现概率密度曲线的图形是单峰式的,即只有一个众值,在峰顶两旁的出现概率密度逐渐减小,且曲线的两端或者一端与横轴渐近相切,基于此,他建立了概率密度曲线的微分方程式:

如果将坐标原点移动至波高序列变量的实际零点,则可以得到Person Ⅲ型曲线的常见形式:

式中α、β、a0为待定参数,他们与统计分析量均


根据上述Person Ⅲ型分布的方法,对于波高模拟值结果,使用与上述Gumbel 分布拟合所用相同的数据,得到的拟合结果如图2 所示。图中黑色点表示的是波高模拟结果,红色曲线表示根据Gumbel 分布函数得到的预测曲线,两条线的拟合程度的相关系数(R)为0.83,均方根误差(RMSE)为0.20,表明Person Ⅲ型分布对于本地波高极大值的拟合程度较好,同样可以作为预测预报的参考。其横纵坐标的含义同图2 的Gumbel 分布是一致的。
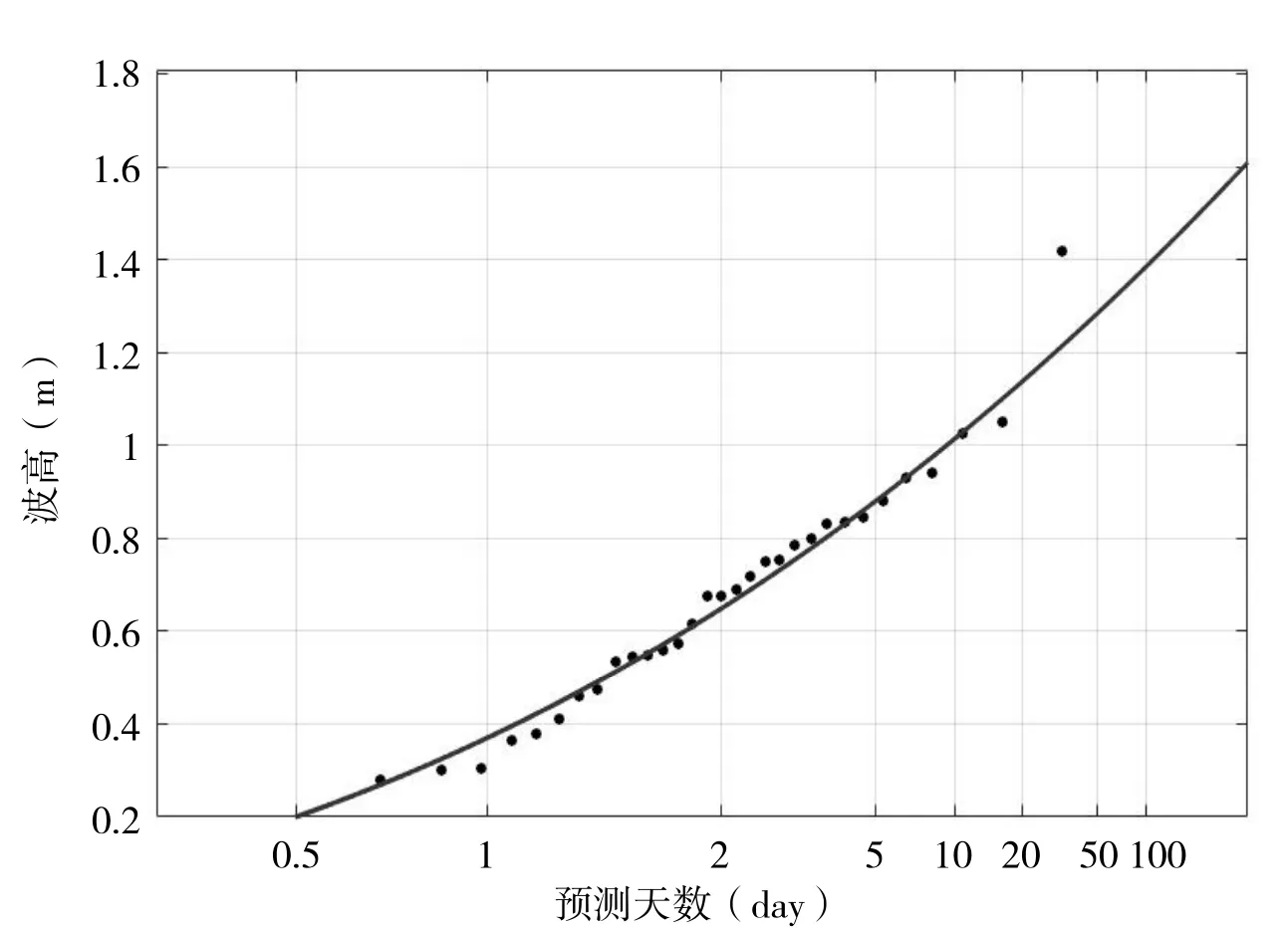
图2 模拟波高与Person Ⅲ型分布拟合结果
综合Gumbel 和Person Ⅲ型两种分布来看,两种方法均能较好地拟合波高的模拟值情况,但是有所区别:对于预测时间较长的情况下(如30 天以上),Gumbel方法预测的极端大值更贴合于实际的模拟结果,曲线形状更为上扬,这也决定了其对于较短预测天数情况下(如30 天以下)的波高极端值会偏大。而Person Ⅲ型分布方法恰好相反,其曲线特征腹部与实际模拟结果更为贴合,对于短预测天数情况下(如30 天以下)的波高极端值拟合更好,对于长期(如30 天以上)的预测结果会偏小一些。
3 结论及应用
本文首先使用欧洲天气预报中心(ECMWF)风场,利用SWAN 数值模型再现了黄渤海海域的波高分布情况,然后与成山头测站的实测波浪值进行对比,相关性表明模拟的结果较好,肯定了在黄渤海海域根据实时风场或者预报风场进行波高预测的可行性。
由于气象风场预测的时长有限性,结合测站测点覆盖的局部性,因此使用统计学的方法,对于黄渤海海域全局模拟的波高进行统计学分析,利用Gumbel 型分布函数Person Ⅲ型分布函数来进行极端波高的预测预报,并根据拟合的结果,判定当需要预测的波高天数大于30 天时,推荐使用Gumbel 分布,当需要预测的波高天数小于30 天时,推荐使用Person Ⅲ型分布。这种综合判断分析预报的方法,可以更好地为后续与波高有关的工程建设、民商互动和船舶作业提供参考决策。
