基于现场监测成果的隧道洞口塌方段处理效果分析

2022-09-28郝付军黄阿岗

地质与勘探 2022年5期

郝付军，黄阿岗

(陕西铁路工程职业技术学院，陕西渭南 714099)

0 引言

隧道洞口段围岩自稳能力相对较差，易发生塌方灾害。为保证进洞安全，开展隧道洞口段塌方灾害的相关研究显得格外重要(陈伟等，2018；吴大勇，2020；李世琦等，2020；宋洋等，2020；张艺腾等，2020)。在以往隧道洞口段的研究中，杨林等(2020)、李广林等(2020)开展了隧道洞口段的加固处理措施研究；崔光耀等(2020)研究了洞口段的注浆加固措施。前人研究多偏向于隧道洞口段的加固措施研究，欠缺隧道洞口塌方段处置后的效果分析，进而仍需进一步拓展研究隧道洞口塌方段的处置效果研究。由于监控量测是隧道施工过程中的必要手段，基于隧道现场变形监测数据来构建洞口塌方段的处置效果分析模型具有较强的可操作性。隧道洞口塌方段的处置效果分析可从两方面着手，其一，是通过构建累计变形预测模型来评价其发展趋势；其二，则是利用隧道变形速率趋势分析来判断隧道变形的增加速率。在累计变形预测模型的构建过程中，考虑到现场监测条件，隧道变形数据常含有一定的误差信息，其对预测效果具有一定影响，因此，在变形预测前，需先对隧道变形数据进行趋势项和误差项的信息分解，且据罗亦泳等(2020)的研究成果，变分模态分解模型具有较强的信息分解能力，可利用其实现隧道变形数据的趋势项和误差项分解。同时，由于隧道变形数据具有显著的非线性特征，单一预测模型难以保证预测精度，鉴于组合预测模型具有较高的预测精度及稳定性(贺华刚，2019)，可在隧道变形数据信息分解基础上，以灰色模型和优化核极限学习机构建累计变形的组合预测模型。在变形速率趋势分析过程中，李常茂等(2018)验证了Spearman秩次检验具有操作简单、准确性高等优点，适用于变形序列的趋势判断，可利用其实现隧道变形序列的趋势分析。

本次研究主要包含两部分，其一是通过变分模态分解模型、灰色模型和优化核极限学习构建累计变形预测模型，其二是利用Spearman秩次检验进行变形速率的趋势分析，并综合对比两者结果，以实现隧道洞口塌方段的处理效果分析。

1 基本原理

结合前述思路，可将分析过程划分为两个步骤，即累计变形预测分析和变形速率趋势分析。

1.1 累计变形预测模型的构建

该步骤主要是对累计变形进行组合预测研究，其过程可细化为：先利用变分模态分解(Variational Mode Decomposition，VMD)实现隧道变形数据的趋势项和误差项分解；再利用灰色模型实现趋势项预测，并将预测误差叠加至前述分解的误差项中，以得到新的误差序列；最后，利用优化核极限学习机(Kernel Extreme Learning Machine，KELM)实现误差序列预测，并将其预测结果叠加至趋势项预测结果，即可得到变形预测的最终预测结果。通过隧道累计变形的组合预测研究，旨在掌握累计变形的发展趋势。

受监测环境限制，隧道变形数据不仅含有一定的误差信息，还具有较强的非线性特征。前者会对预测效果具有一定影响，侧面说明有必要对变形数据进行信息分解处理，而后者致使单一预测模型难以完全刻画其变形规律，需对其进行组合预测研究(罗林等，2014；赵淑敏，2018；石州等，2020；王永刚等，2020)。

1.1.1 信息分解模型的构建

在塌方段的变形监测过程中，扰动因素相对较多，如施工因素、人为因素等，都会造成变形数据含有一定的误差信息，即：

yi=ri+εi

(1)

式中：yi为变形监测值；ri为趋势项；εi为误差项。

VMD模型是一种新型多尺度时频分析方法，具有非递归自适应性和准正交分解方式，计算效率较高。因此，利用其实现隧道变形数据的信息分解是可行的，其基本分解流程已在相关文献详述(罗亦泳等，2020；陈竹安等，2020；鲁铁定和谢建雄，2021)，不再赘述。

由于VMD模型的模态数和惩罚参数等多由使用者确定，主观性较强，为保证其最优性，考虑到遗传算法(Genetic Algorithm,GA)的全局优化能力，利用其实现VMD模型的模态数和惩罚参数优化，将其优化过程分述如下：

(1)初始参数设置，如规模参数、交叉及变异等因子，并将其遗传因子解码，以获得初始隐层数和窗口大小参数。

(2)结合样本分布，将遗传算法寻优过程中的样本划分为训练集和验证集，并将其输入到VMD模型中，实现验证集的误差指标验算。

(3)若误差指标达到期望要求时，则停止寻优，输出优化结果；反之，对遗传因子进行交叉、变异处理，实现遗传信息的更新替换，直至满足期望要求。

同时，在以往信息分解效果的评价过程中，多以信噪比为评价指标，但考虑到未明确变形数据中的趋势项和误差项，使得利用信噪比进行评价具有一定的不合理性。结合信噪比的评价原理，引入降噪误差比dnSNR：

dnSNR=10×lg(Ps/Pg)

(2)

式中：Ps为包含误差因素的序列功率；Pg为滤除误差因素的序列功率。

一般认为，降噪误差比dnSNR值越小，说明信息分解效果越好；反之，说明信息分解效果越差。

1.1.2 趋势项预测的模型

灰色GM(1,1)模型具有较强的模糊判别能力，利用其实现隧道变形数据的主趋势项预测是可行的(胡达等，2017；张云鹏等，2018；袁志明等，2020；张锦等，2021)。据GM(1,1)模型的基本原理，先对趋势项序列进行累加处理，得到其一次累加序列x1：

x1=(x1(1),x1(2),…,x1(n))

(3)

式中：x1(n)为累加序列值。

对一次累加序列x1进行求导处理，得到GM(1,1)模型的白化方程为：

dx1(k)/dt+ax1(k)=b

(4)

式中：a、b为待解常数。

通过最小二乘法求解常数a、b，得式(4)的响应序列为：

x1(k+1)=[x0(1)-b/a]e-ak+b/a

(5)

最后，对累加序列进行反向递减处理，即可实现趋势项预测。值得指出的是，GM(1,1)模型的趋势项预测结果会存在一定误差，将其叠加至前述分解处理的误差项，以组成新的误差序列。

1.1.3 误差序列预测模型的构建

核极限学习机(Kernel Extreme Learning Machine，KELM)是一种新型神经网络，属ELM神经网络的改进型，主要提升了网络训练速度及泛化能力，具有显著优势，已被广泛应用，非线性预测能力较强，可利用其进行误差序列的变形预测。鉴于相关文献(高彩云，2017；张志会，2018；王雪妮和韩国锋，2018；陈艳茹，2018；陈颖等，2018；杨芳等，2021)已对KELM模型的基本原理进行详述，限于篇幅，该文不再赘述。

在KELM模型的应用过程中，正则化系数和核函数由使用者确定。为保证其客观性，提出利用改进粒子群算法进行优化处理。粒子群算法(Particle Swarm Optimization，PSO)是一种智能随机优化算法，收敛速度较快，但因其迭代次数增加，会使个体粒子具有较强相似性，易陷入局部极值问题。为解决该问题，HPSO算法应运而生，其主要是利用遗传算法的交叉、变异处理来实现粒子间的信息交换，进而保证粒子多样性，避免陷入局部极值问题。结合KELM模型和HPSO算法的基本原理，将误差序列的预测流程详述如下：

(1)对KELM神经网络的基本参数进行合理设置，如输入及输出层个数、隐层节点数等，即确定出KELM神经网络的网络拓扑结构。

(2)初始化粒子群参数，如将粒子群规模设置为500，粒子维数设置为2，分别代表正则化系数和核函数，最大迭代次数为600次，其他参数随机设置。

(3)将预测误差作为适宜度函数，并对比全局与粒子的适宜度值，当前者更优时，改变粒子位置及速度，继续迭代寻优；反之，用粒子适宜度值替换全局适宜度值。

(4)对粒子进行交叉、变异处理，以改变粒子位置和速度，保证粒子位置、速度的多样性。

(5)当达到期望误差或最大迭代次数时，停止迭代，将最优全局适宜度值对应的正则化系数和核函数输出作为KELM模型的对应参数。

最后，将前述趋势项预测结果和误差序列的预测结果叠加，即为隧道变形的最终预测结果。

1.2 变形速率趋势分析模型的构建

该步骤主要是对变形速率进行发展趋势分析，其实现方法是Spearman秩次检验。通过变形速率的趋势分析，掌握隧道变形速率的增加速度，也借此来佐证前述累计变形预测结果的准确性。

由于Spearman秩次检验法具有操作简单、准确性高等优点，可合理评价变形序列的发展趋势，因此，利用其构建隧道变形速率的发展趋势评价模型(鞠兴华等，2018；徐金英和胡明庭，2019；王佃来等，2019)。将隧道变形速率序列表示为{Xi；i=1,2,…,n}，对其进行大小排序，得新序列为{Yi；i=1,2,…,n}，通过两序列计算得到其秩系数rs为：

rs=1-[6∑(Xi-Yi)2]/[n3-n]

(6)

式中：n为样本总数。

rs值的趋势性判据为：若rs<0时，说明隧道变形速率具下降趋势；若rs>0时，说明隧道变形速率具上升趋势。

同时，rs值越大，其趋势性越显著，进而以相应检验水平对应的临界值Wp为基础，进行隧道变形速率发展趋势的等级评价，划分标准如表1所示。

表1 变形速率的趋势性等级划分标准

对比累计变形预测结果和变形速率趋势分析结果，两者相互佐证，并综合判断隧道洞口塌方段的处理效果，效果判据为：若隧道变形无明显增加趋势，并趋于稳定方向发展，说明塌方处理方式是合理有效的；反之，若隧道变形仍继续增加，则应继续监测，并视变形程度增加相应的加固措施。

2 实例分析

2.1 工程概况

小寨山隧道隶属临清高速六标段，位于勐简乡大寨村，左线里程：ZK82+860 m～ZK85+984 m，长度为3124 m，最大埋深为557 m；右线里程：ZK82+899 m～ZK86+000 m，长度为3101 m，最大埋深为554 m。据勘察成果，隧址区具高中山地貌，高程间于940～1514 m，高差约574 m，地形起伏较大，斜坡坡度间于10°～35°，利于降雨汇集。

根据地质调查和钻探成果，隧址区第四系土层以粉质黏土和断层角砾岩为主，对隧道工程施工影响较小；下覆基岩主要为三叠系、二叠系及古生代岩层，岩性有灰岩、白云岩和片岩，其中，片岩主要位于洞身段，对隧道施工影响较大。同时，隧址区地质构造也较为复杂，发育有较多的断裂构造，主要为云阳-大寨断裂，对隧道施工影响较大。

在隧道洞口段ZK82+870 m～ZK82+882.6 m，洞身埋深为3～6 m，相对较浅，且地形不对称，于2018年7月10日，隧道管棚出现裂缝，随之地表也发生变形，并出现塌方灾害。

为保证后续施工的安全进行，对塌方段进行了防治处理，措施可简要总结为：

(1)地表加固处理措施。由于降雨是洞口段塌方的重要诱因，先对地表变形裂缝进行封填处理，并铺设钢筋网，喷射混凝土，保证降雨不再入渗。

(2)地形偏压处理措施。偏压也是本次塌方的重要诱因。为避免该因素对后续施工影响，对其地形进行反压回填处理，以使隧道围岩压力均衡，且在回填过程中，保证回填密实度，并设置排水沟，避免降雨造成水土流失。

(3)开挖掘进加固措施。由于塌方段围岩已出现变形破坏，其自稳能力也已趋于减弱，需对初支进行加固设计，如增加拱脚锁强，避免应力集中影响；增加钢拱架强度，保证初支的支撑能力；优化仰拱开挖时，应尽量避免初支悬空。

为合理评价上述处理效果，也为实现信息化施工，在塌方段掘进过程中，也进行了现场变形监测。其中，ZK82+877 m断面和ZK82+880 m断面的数据较为完善，其监测项目为拱顶沉降和水平收敛，监测频率为1 d/次，共计得到30 d的监测成果，具体详见表2。据表2，ZK82+877 m断面的拱顶沉降相对于水平收敛具有相对更大的增加速率，且变形增加的持续时间也相对更长，其中，拱顶沉降变形值为45.20 mm，而水平收敛变形值为20.70 mm；在ZK82+880 m断面的前期变形中，水平收敛的增加速度要大于拱顶沉降的增加速度，而后期则相反，据统计结果，得拱顶沉降变形值为53.80 mm，而水平收敛变形值为33.63 mm。

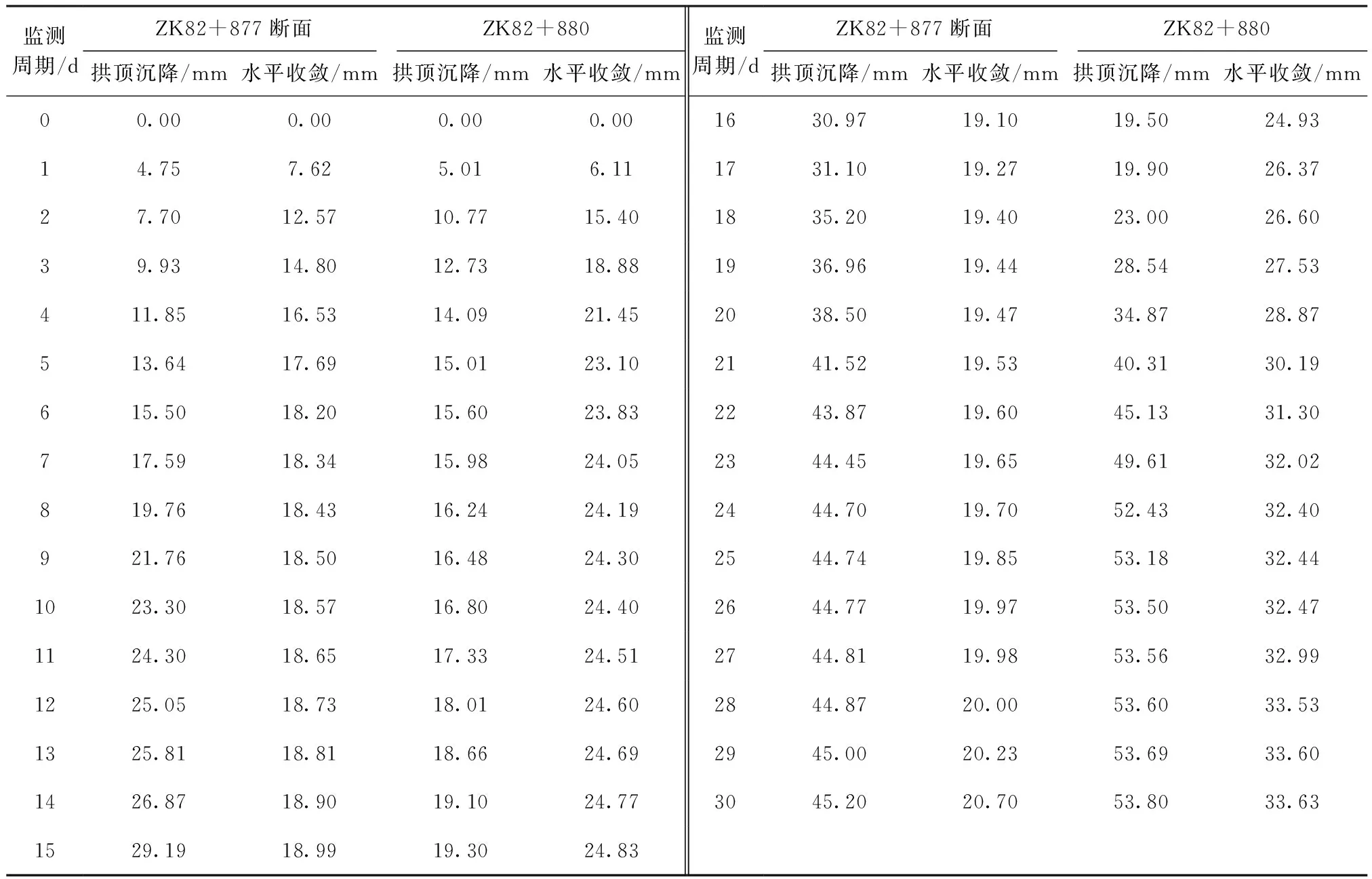
表2 隧道变形监测成果

2.2 累计变形预测分析

在累计变形预测过程中，以ZK82+877 m断面的拱顶沉降为例，详述信息分解过程和不同阶段的优化过程，并根据研究思路，可进一步将累计变形预测过程划分为三个步骤，具体分述如下：

(1)信息分解处理

首先，为验证VMD模型相较于传统卡尔曼滤波和EMD模型的优越性，将三种模型均进行隧道变形数据的信息分解处理，得三者结果如表3所示。据表3，三种信息分解模型的评价指标值存在一定差异，其中，VMD模型的dnSNR值相对最小，值为14.15，说明其分解效果相对最优，其次是EMD模型和卡尔曼滤波，验证了VMD模型相较于传统模型具有显著的优越性。

表3 不同信息分解模型的结果对比

其次，再利用遗传算法对VMD模型进行优化处理，得优化前后的处理结果如表4所示。据表4，经遗传算法的优化处理，所得GA-VMD模型对应信息分解结果的dnSNR值为12.73，较优化前具有进一步的减小。这说明通过遗传算法的优化处理，能有效提高隧道变形数据的信息分解效果。

表4 VMD模型优化前后的分离效果对比

概言之，VMD模型在隧道变形数据的信息分解过程中具有明显的优越性，且通过优化处理能进一步提升其分解能力。因此，以GA-VMD模型进行隧道变形数据的信息分解是可行的，即利用其将隧道变形数据分解为趋势项和误差项。

(2)变形预测分析

在变形预测过程中，以1～25 d的监测数据为训练样本，26～30 d的监测数据为验证样本，外推预测周期数为4期。先利用GM(1,1)模型对ZK82+877 m断面的拱顶沉降进行趋势项预测，结果如表5所示。据表5，在趋势项的预测结果中，相对误差间于2.08%～2.37%，平均相对误差为2.22%，预测精度一般，侧面说明后续进行误差弱化预测的必要性。

表5 ZK82+877 m断面拱顶沉降的趋势项预测结果

再利用HPSO-KELM模型进行误差序列的变形预测，且为对比PSO算法和HPSO算法的优化效果，对两者的预测结果均进行统计，得表6。

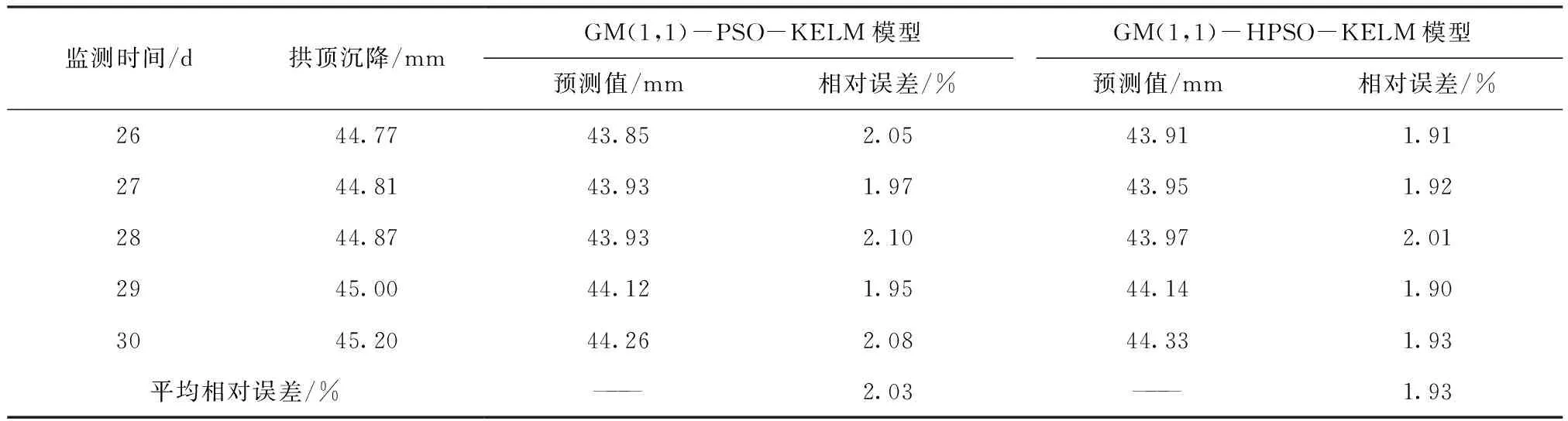
表6 ZK82+877m断面拱顶沉降的最终预测结果

据表6，在相应验证节点处，GM(1,1)-HPSO-KELM模型的预测结果具有更小的相对误差，且其平均相对误差为1.93%，也小于GM(1,1)-PSO-KELM模型的2.03%，说明HPSO算法较PSO算法具有相对更优的预测效果，对预测精度的提升作用更大。

最后，再利用GM(1,1)-HPSO-KELM模型对两监测断面的所有监测项目进行变形预测，得预测结果如表7所示。据表7，两监测断面在不同监测项目中的相对误差均值间于1.91%～1.99%，都具有较高的预测精度，充分说明GM(1,1)-HPSO-KELM模型在隧道变形预测中的适用性。同时，四个监测项目的外推预测结果均表现为：随监测时间持续，变形值无明显增加趋势。

表7 两监测断面的最终预测结果

(3)优越性验证

前述已初步验证了GM(1,1)-HPSO-KELM模型的有效性。为进一步验证其相对传统神经网络的优越性，再利用BP神经网络和RBF神经网络进行同样的变形预测，经统计，得三者的特征参数如表8所示。据表8，在相应验证断面或监测项目处，该文预测模型具有相对最小的相对误差均值及更少的迭代次数。尤其在迭代次数方面，本文预测模型在不同监测项目中的变化差异不大，而其余两类预测模型均具有较大的波动性，说明本次预测模型相较于两类传统神经网络具有更优的预测精度和收敛速度，进一步验证了本次预测思路的合理性和有效性。

表8 不同预测模型的效果对比

通过上述研究，得出组合预测能有效保证预测精度，构建的GM(1,1)-HPSO-KELM模型适用于隧道变形预测。预测结果显示，隧道洞口塌方段经处理后，其累计变形的后期具一定增加趋势，但增加速率相对较小，并不显著。

2.3 变形速率趋势分析

据研究思路，再利用Spearman秩次检验进行隧道变形速率的趋势分析，先以已有变形监测成果进行Spearman秩次检验，得两监测断面的检验结果如表9所示。据表9，四个监测项目的rs值均小于0，得四者的变形速率具下降趋势，其中，ZK82+877断面水平收敛的趋势等级为Ⅰ级，其余三个监测项目的趋势等级均为Ⅱ级，得出隧道变形速率趋于减小，且趋势性较为显著。