中低速磁浮车辆侧向通过道岔动力学性能影响因素分析

赵逸凡，赵春发，彭也也，冯洋

中低速磁浮车辆侧向通过道岔动力学性能影响因素分析

赵逸凡，赵春发*，彭也也，冯洋

（西南交通大学 牵引动力国家重点实验室，四川 成都 610031）

为了探究中低速磁浮车辆侧向通过道岔时动力学性能的影响因素，采用UM软件建立了中低速磁浮车辆－侧向位道岔耦合动力学模型，车辆动力学模型中详细考虑了支承台、迫导向机构、电磁铁横向滑橇以及主动控制的PID悬浮控制系统，同时建立了考虑主动梁、从动梁、角平分装置以及F轨的磁浮道岔有限元模型。采用长沙磁浮快线提速试验数据验证车辆动力学模型后，对比分析了10 km/h速度工况下角平分装置以及滑动支承台行程对于磁浮车辆侧向过岔时系统动力学响应的影响。仿真结果表明，若道岔连接处未设置角平分装置，系统响应将整体增大，其中车体前端横向加速度幅值增大约40%。扩大滑台行程30 mm后，系统的横向响应明显减小，电磁铁横移量减小10.70 mm，可较为有效的避免磁轨机械接触以及悬浮失稳等情况。综合考虑磁浮车辆侧向过岔的动力学性能，在道岔连接处设置角平分装置可有效提高车辆运行时的平稳性与安全性，同时在实际情况允许下可增大滑台行程进一步优化侧向过岔时的系统响应。

磁浮车辆；关节型道岔；侧线；角平分装置；滑动支承台

近年来，中低速常导电磁悬浮型磁浮交通由于其安全性强、造价较低以及环境适用性强等优势，在国内外快速发展并逐渐进入人们的视线[1-4]。不同于传统铁路车辆中的轮轨接触运行，中低速磁浮车辆抱轨运行，利用主动控制的悬浮力悬浮在轨道上，并通过电磁铁横移产生提供的横向回复力作用进行导向。考虑到中低速磁浮车辆特有的运行方式，目前已开通的商业运营线路中道岔结构多借鉴跨坐式单轨交通中的道岔型式，采用三段铰接的双腹板焊接钢结构道岔[5-8]。钢结构的设置减小了道岔梁自重，降低了换线难度，但同时由于阻尼小、约束弱的特点，在早期工程运用中，列车在通过时易发生强烈的车－岔耦合振动，最严重时甚至导致悬浮控制系统失稳以及电磁铁砸轨等危及行车安全性情况发生。为了优化过岔时安全性及平稳性，实际工程中采用了增设沙袋、加装调谐质量阻尼器、增设主动梁中间台车等方式减缓车－岔间的耦合振动[9-14]，但这些被动减振措施增加了道岔安装与维护的成本。一些学者针对中低速磁浮车辆与道岔梁强烈耦合振动机理及减振对策的相关问题，开展了有关的现场试验以及数值仿真研究[15-19]，结果表明行车速度、道岔梁体阻尼与悬浮控制参数等因素均会对系统响应产生重要的影响。

目前道岔现场试验主要是针对振动过大问题进行减振方法的探究，而中低速磁浮车辆与道岔耦合振动的仿真分析研究，主要针对列车直线过岔情况。然而，对于磁浮车辆与侧向道岔耦合振动的研究较少。当道岔处于侧向位时，三段道岔梁体拟合曲线半径约为100 m左右，由于道岔区未设置超高，所以在侧向通过道岔时，磁浮车辆与线路的关系会变得更加严峻。在实际的工程运用中，已经在道岔区F轨发现划痕，说明车辆侧向过岔时电磁铁横向滑橇与F轨之间发生了机械接触，同时也已发现侧向通过道岔时提速较为困难、车体横向明显抖动等情况，说明磁浮车辆侧向过岔安全性问题需要解决，很有必要对其耦合振动机理进行研究，并寻找出影响动力学响应的相关因素。

本文结合国内某建设中的磁浮工程线路项目，首先建立了考虑支承台、迫导向机构、电磁铁横向滑橇、牵引拉杆以及PID控制的车辆动力学模型，以及两种均包含主动梁与两跨从动梁的磁浮道岔有限元模型。其次仿真计算了10 km/h速度下两节编组磁浮列车侧向通过道岔时的系统动力学响应，作为对照研究分析了角平分装置与滑动支承台行程对车—岔系统响应的影响。最后，对文章提到的两种影响因素进行了总结分析与规律总结，以期为我国中低速磁浮交通道岔系统的安全运用与结构优化提供理论依据和应用参考。

1 磁浮车辆动力学模型

1.1 车辆动力学模型

中低速磁浮车辆由车体、支承台、迫导向机构、二系悬挂装置、悬浮架以及相关电气控制设备等组成[20]。车体约为15 m，下方设置有5位悬浮架，每位悬浮架又由左、右两悬浮模块通过两者间的防侧滚装置进行连接。悬浮模块主要由侧梁、托臂及悬浮电磁铁等组成，负责完成车辆运行中的牵引制动与悬浮导向；防侧滚装置组成主要包括防侧滚梁与吊杆，允许左右模块间的非侧滚运动。各悬浮模块前后端均设置了空气弹簧（下文中简称空簧），其上部安装座与支承台连接，支承台又与车厢下部进行连接，单节磁浮车辆共设置了6位支承台，除1位悬浮架前端及5位悬浮架后端空簧与支承台单独连接外，其余位置均是由前后相邻的两空簧连接于同一支承台。处于车厢下部不同位置的支承台具有不同的自由度，其中1、3、4、6位支承台可以相对车体横向移动，被称为滑动支承台（下文中简称滑台），2、5位支承台与车体固接，被称为固定支承台。滑台受到迫导向机构作用后进行运动，迫导向机构可以有效提升磁浮车辆的曲线通过性能，主要由横向拉杆、前后T型臂以及钢缆组成，T型臂可绕安装在车厢底部的旋转中心进行转动，且前T臂的长度一般位后T臂的两倍。图1为平面曲线上磁浮车辆迫导向机构的工作状态示意图。

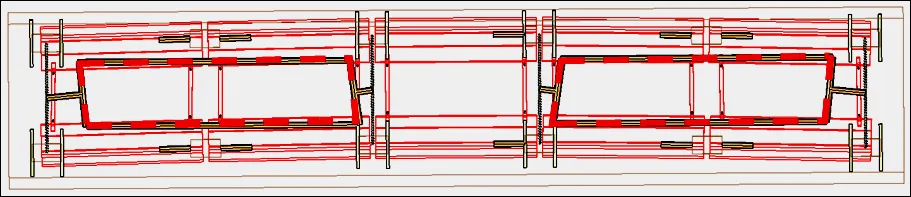
图1 平面曲线上迫导向机构的工作状态

针对上述中低速磁浮车辆结构，如图2所示采用多体动力学软件UM对中低速磁浮车辆动力学模型进行了建模，车体与悬浮模块均设置除纵向平动外的5个自由度，考虑了滑台相对车体横向运动自由度以及悬浮模块间除侧滚外的相对运动，整车模型共包括131个运动自由度。在建模时未考虑车体结构件的柔性变形，空气弹簧考虑为简单的线型弹簧－阻尼器。为了更好的模拟电磁力的分布，将每个线圈绕组上均匀分布的电磁力等效为5个集中力。此外，在悬浮模块前、后两线圈绕组间设置了横向滑橇，与F轨之间的初始间隙设置为13.3 mm。采用相同方法建立了两节编组的磁浮列车动力学模型，表1给出了中低速磁浮车辆动力学模型的主要参数。

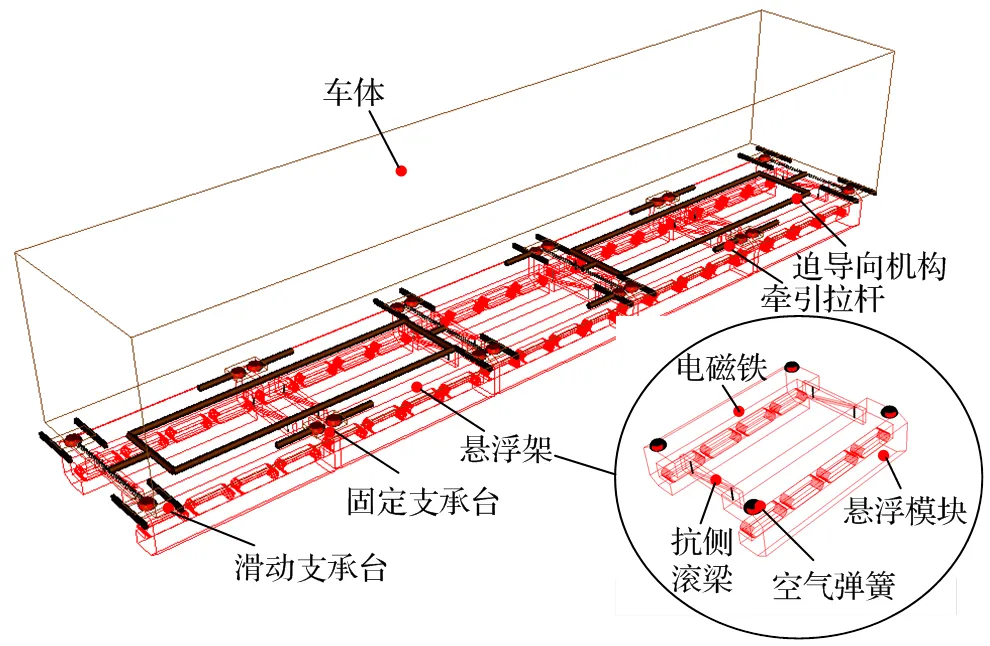
图2 中低速磁浮车辆动力学模型

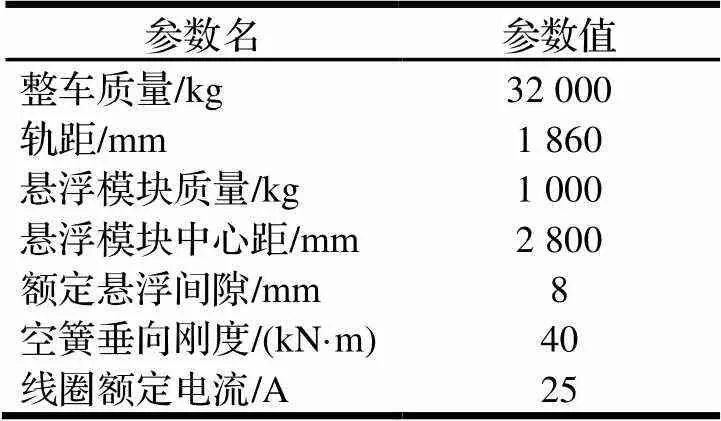
表1 磁浮车辆动力学模型参数

1.2 电磁力计算模型

中低速磁浮车辆通过U型电磁铁与F轨之间的吸力作用进行悬浮，转向时电磁铁相对F轨横向移动，在横向上产生横向回复力进行导向。工程运用中，电磁铁内设置4个线圈绕组，前后两绕组分别受控于两个独立的悬浮控制器。在忽略磁饱和与磁泄露并假设整个电磁铁悬浮间隙均匀的前提下，可以采用以下公式对电磁铁悬浮与横向回复力进行计算[21]：

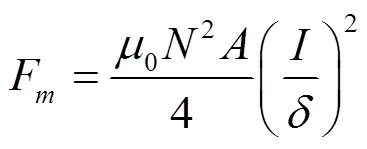
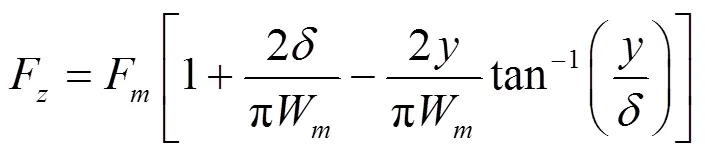
根据目前已有研究，中低速磁浮车辆的电流控制主要通过包含位置环与电流环的双环控制器，由于电流环主要用于减小控制系统中的电流延时，一般在动力学仿真中可忽略其影响。位置环主要基于电磁铁悬浮间隙，通过比例－积分－微分（PID）控制回路电压进行控制。对于电磁铁线圈绕组电流，其控制规律可表示为：

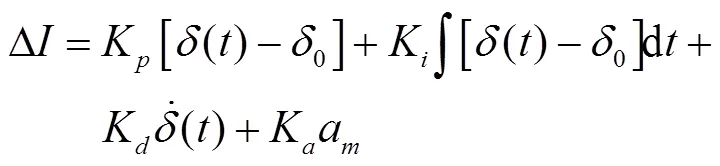
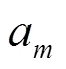
根据上述控制器的设置原理，使用Matlab/Simulink和UM软件之间的接口，将PID控制模型导入建立好的磁浮车辆动力学模型中，实现悬浮和导向控制系统的动态仿真。

1.3 车辆动力学模型验证

由于论文依托的实际工程项目目前尚无磁浮列车侧向通过道岔时的系统响应实测数据，为保证计算结果可靠性，采用1.1节中建立的车辆动力学模型，仿真计算140 km/h速度下通过长沙磁浮快线磁浮简支梁时车体动力学响应，与笔者所在科研团队于2021年长沙磁浮快线提速试验中实测的车辆系统响应结果进行比对（图3）。仿真得到车体前端垂向与横向加速度幅值分别为0.643 m/s2和0.269 m/s2，试验实测值加速度分别为0.630 m/s2与0.281 m/s2，误差分别为2.06%与4.27%；仿真与实测结果响应幅值及波形均吻合较好，说明本文建立的磁浮车辆动力学模型较为可靠。

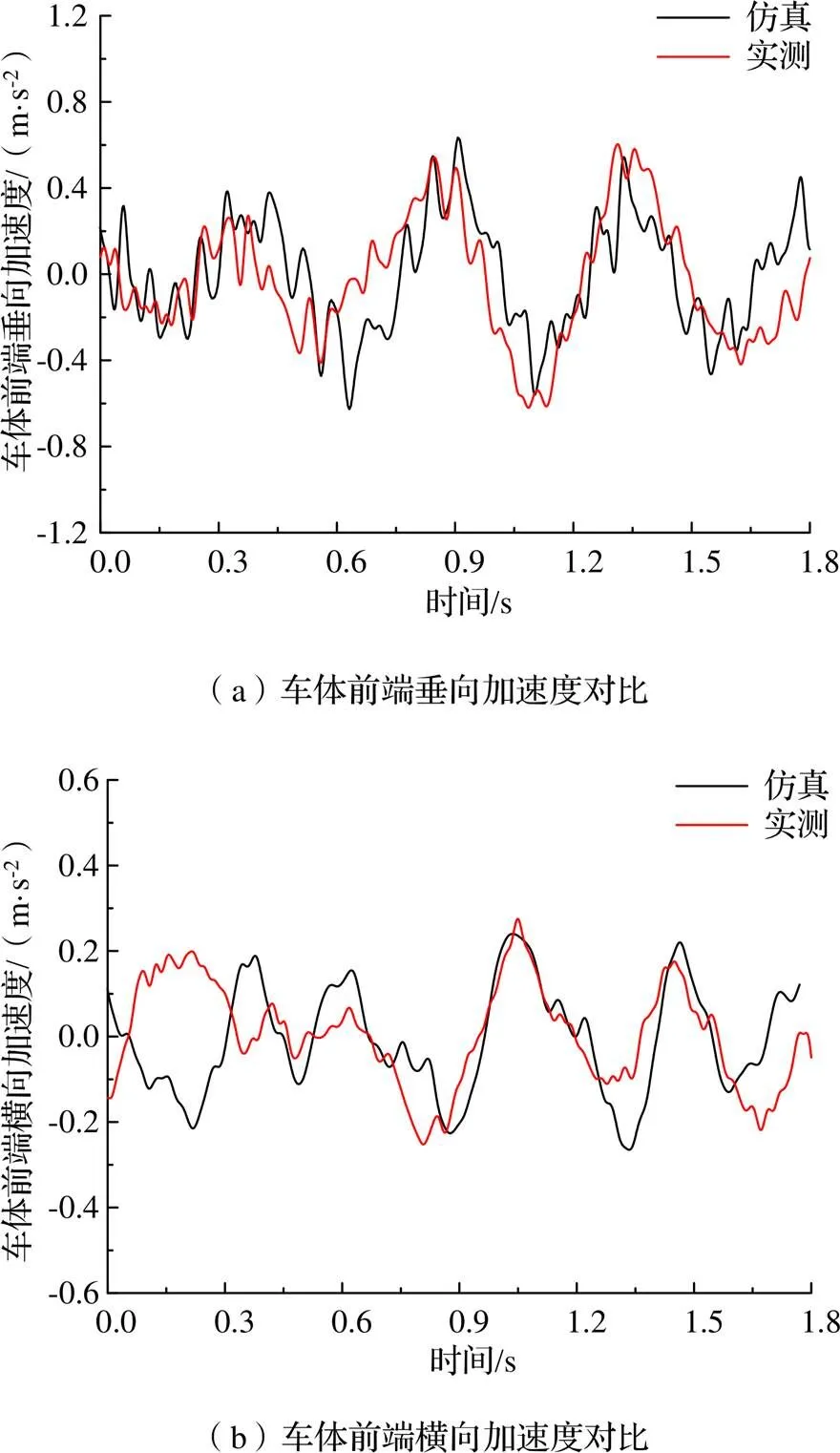
图3 仿真与实测结果对比

2 磁浮道岔侧向位有限元模型

图4给出了磁浮道岔结构示意图。由图可见，中低速磁浮道岔主要由主动梁、第一从动梁、第二从动梁、垛梁、梁端固定装置、走行台车、驱动装置、锁定装置、基础支撑、电气和信号系统等组成。主动梁长约为19.8 m，跨中处梁高约为1.8 m，梁体内设置横隔板，纵向间距1.2 m；第一、第二从动梁长度分别约为4.8 m与5.0 m，道岔总长约为32 m。道岔切换至侧向位时，主动梁及第一、第二从动梁与正线分别呈6.9°、4.6°及2.3°的夹角，车辆通过的设计速度为25 km/h，实际工程应用中往往不超过15 km/h。

图5为使用有限元建模软件Hypermesh建立的侧向位磁浮道岔有限元模型，模型中详细考虑了主动梁、从动梁、F轨以及道岔梁间F轨的平分角度连接，台车对梁体的约束采用弹簧力元进行模拟。由于道岔结构中板的特征尺寸与厚度之比较大，本文在有限元模型中对道岔与F轨结构均采用壳单元Shell 181建模，共划分2.6万个网格。为了验证有限元模型的准确性，采用作者所在科研团队于2018年在中国铁建重工集团有限公司制造车间测试得到的道岔结构自振频率对道岔有限元模型进校核。根据文献[15]的测试结果，主动梁第一阶横弯频率为8.5 Hz，第一阶竖弯频率为15.7 Hz，而本文采用的有限元模型前二阶模态频率分别为8.70 Hz与15.52 Hz，同样对应主动梁的一阶横弯与竖弯模态，可知道岔结构的第一阶横、竖向模态频率计算值与实测值的相对误差较小，建立的道岔有限元模型准确性较好。

图4 磁浮道岔结构示意图

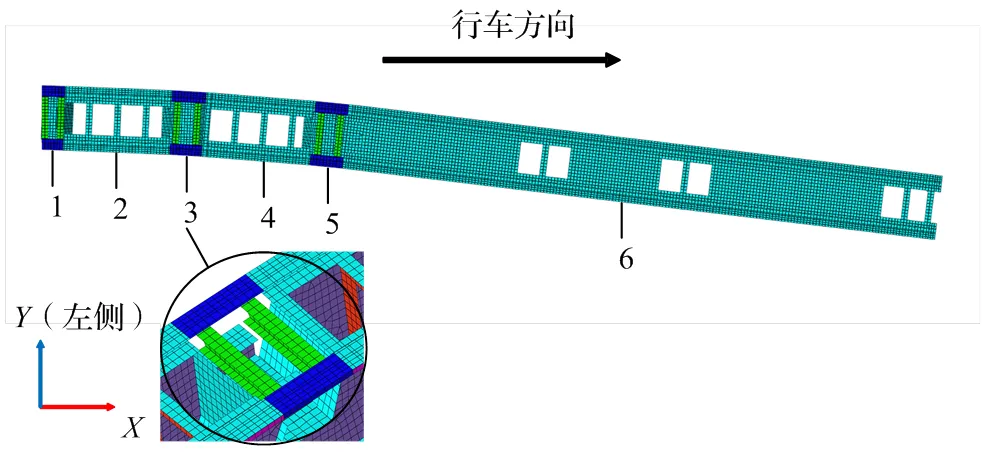
1，3，5.角平分装置处F轨；2.第二从动梁；4.第一从动梁；6.主动梁。

3 角平分装置对车岔系统响应的影响

在中低速磁浮道岔的早期工程运用中，由于未设置角平分装置，导致车辆在侧向过岔时出现较大的冲击。角平分装置的设置使梁间F轨的相对折角变化更加平缓，有效的减小了线路折角带来的冲击，使磁浮车辆过岔更加平稳，本节对比分析了10 km/h速度下车辆通过（未）设置角平分装置的道岔时系统的动力学响应，用以分析其对系统横向动力学的影响。在仿真时柔性道岔梁前后轨道设置为刚性，轨道随机不平顺的选用参考文献[22]，两节编组磁浮列车行车方向为坐标正方向（图5），方向指向前进方向左侧，正方向向上。

3.1 车辆系统响应分析

图6为两节编组磁浮列车以10 km/h速度侧向通过未设置/设置角平分装置道岔梁时，车体前端横向加速度响应的时程对比图。可以看出，取消角平分装置后，车体前端最大横向加速度为2.11 m/s2，已经较为接近GB/T 5599－2019规范[23]中规定的车体振动加速度2.5 m/s2的限值；而设置角平分装置时，车体横向加速度幅值1.50 m/s2，磁浮车辆的侧向过岔过程较为平稳。说明若道岔间未设置角平分装置，将会对车体造成较大的横向冲击，角平分装置的设置可以有效的减缓线路折角，从而提高车辆运行时的平稳性。

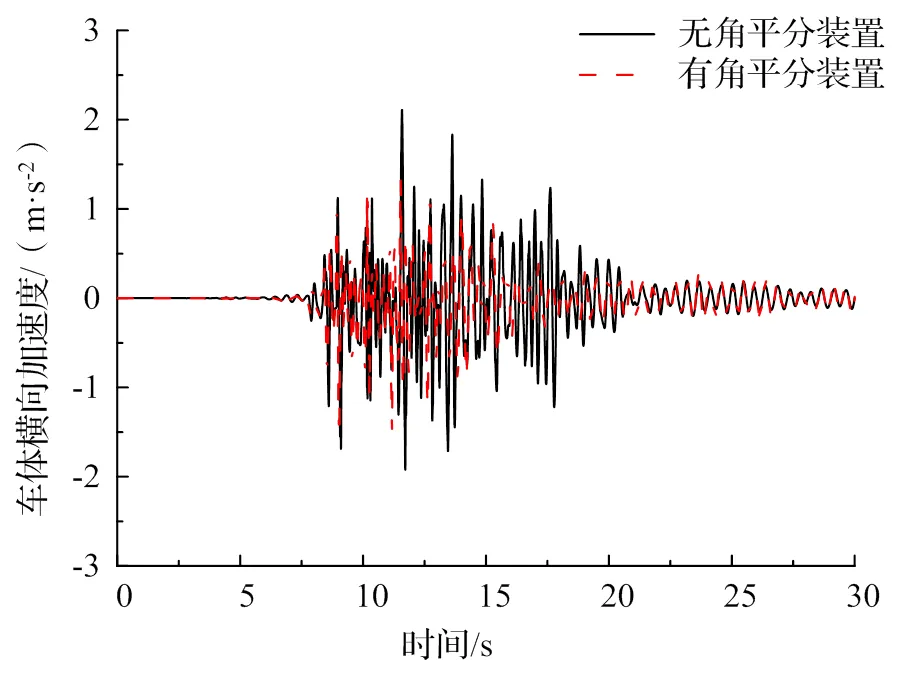
图6 车体前端横向加速度

悬浮架在车辆系统中最先感受到线路变化，图7给出了1位悬浮架在通过（未）设置角平分装置道岔时横向加速度对比图，从图中可以明显看出在未设置角平分装置时，悬浮架在横向上受到了三次明显的冲击，悬浮模块横向滑橇与F轨之间发生了较剧烈的机械接触，时间点分别对应运行至三处道岔间连接处，横向加速度幅值最大可达39.56 m/s2，远大于设置角平分装置时的5.06 m/s2。说明若未设置角平分装置，悬浮架会受到较强的冲击力，可能会减少其使用寿命并增加维护成本，严重时甚至会影响行车的安全性能。

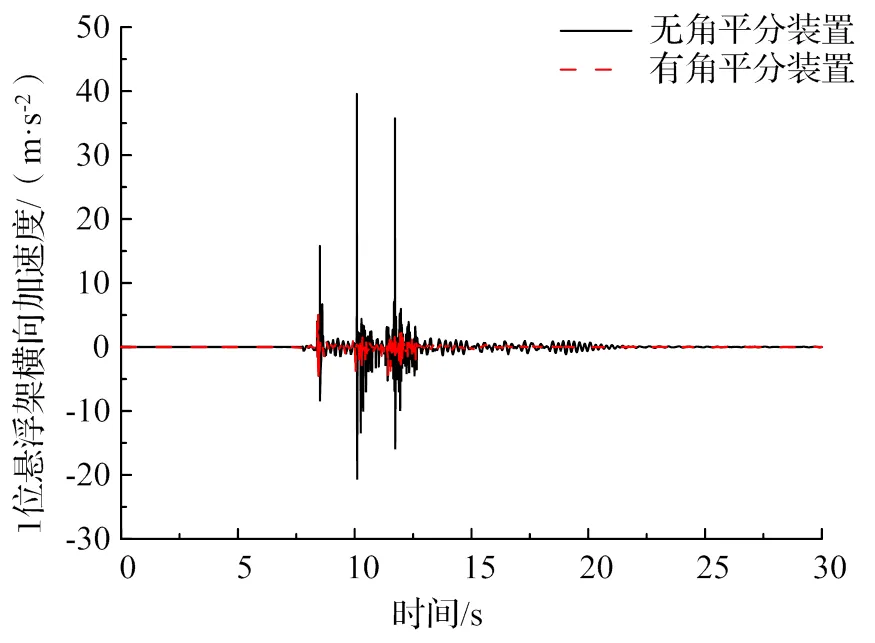
图7 1位悬浮架横向加速度

3.2 道岔系统响应分析

相对于从动梁来说，主动梁长度较长，结构刚度较小，对道岔研究往往主要关注主动梁的各项响应，故本文中不再给出从动梁的响应。图8为道岔主动梁跨中处横向加速度时程曲线对比图，从图中可以得到，取消角平分装置的设置后，跨中处横向加速度幅值由4.10 m/s2增大至6.85 m/s2，同时整个过岔过程中主动梁横向加速度明显增加，说明梁间设置角平分装置可以有效减小道岔梁体的横向加速度响应。

图9给出了中低速磁浮车辆通过侧向位道岔时主动梁跨中处的横向位移响应。从图中可得两种情况下梁体横移均较小，设置角平分装置后梁体横向位移由0.49 mm减少至0.27 mm。通过主动梁的动力学响应对比可得，设置角平分装置有效减小了道岔系统横向响应。

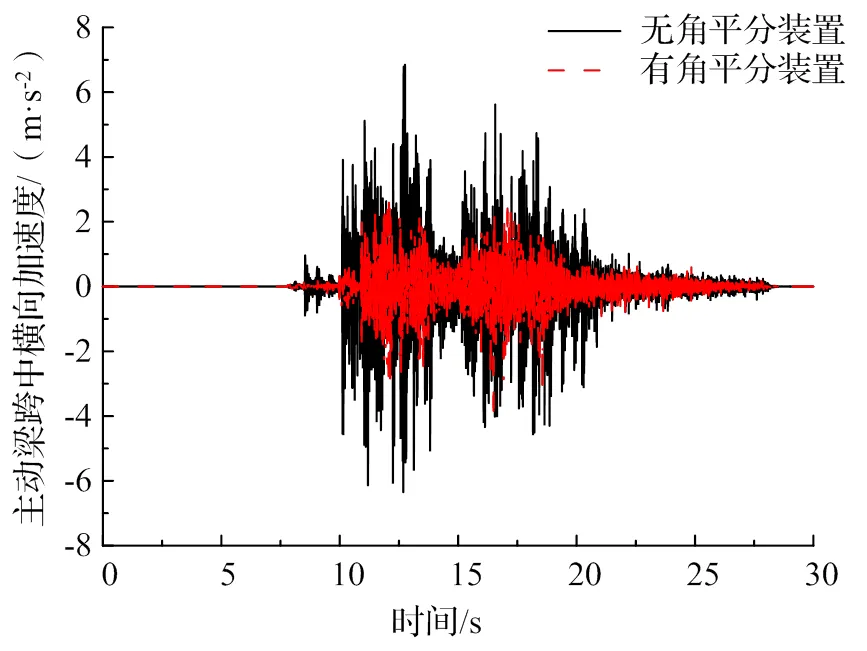
图8 主动梁跨中处横向加速度

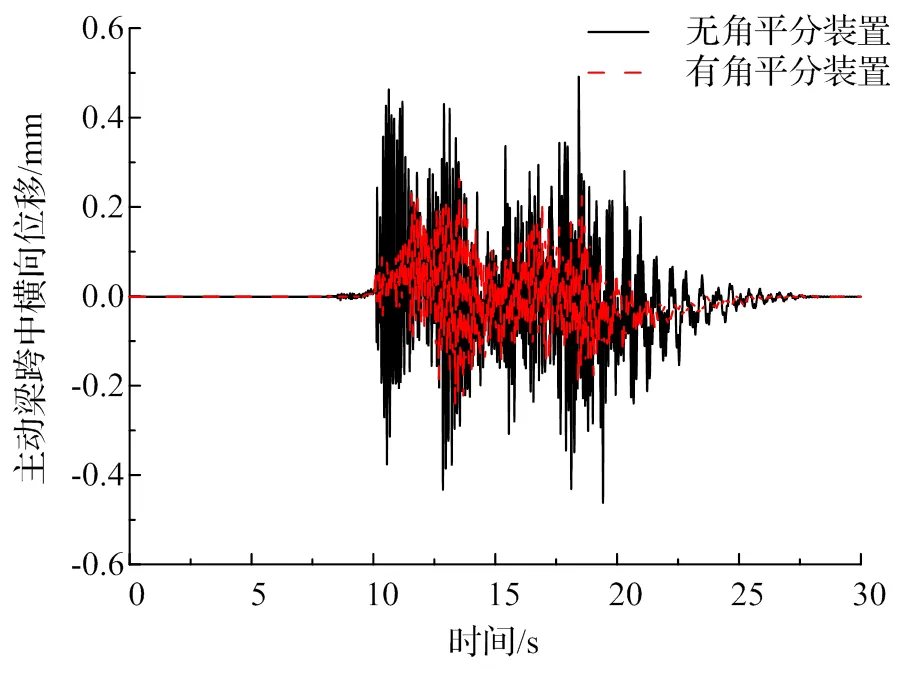
图9 主动梁跨中处横向位移

4 滑台行程对车岔系统响应的影响

中低速磁浮列车车厢下设的滑动支承台可以使悬浮架相对车体进行横向移动，在车辆转向时可减少车体对悬浮架的约束，使悬浮架贴近轨道中心线运动，有利于车辆运行的平稳性与安全性。通常在滑台移动84.3 mm时会接触止挡停止滑动，此时悬浮架与车体的相对运动关系不再存在。本节通过增大滑台行程研究其对系统动力学响应的影响，首先给出滑台行程扩大20 mm后系统响应对比，随后给出了行程扩大10～30 mm时对系统响应的影响规律。

4.1 车－岔系统响应分析

图10为将滑台行程扩大20 mm后车体前端横向加速度响应对比图，在车辆运行时间约9.2 s，滑台行程达到了84.3 mm。9.2 s后滑台行程扩大导致响应出现变化（如图中蓝色线框中所示）。从图中可得，扩大滑台行程后车体前端横向加速度幅值为0.71 m/s2，小于原行程时的幅值1.50 m/s2，车体侧向过岔时更加平稳。

滑台行程扩大后1位悬浮架横向加速度对比如图11所示，车辆运行时间9.2 s后，悬浮架横向加速度明显减小，振动幅值由原滑台行程的4.54 m/s2减小至仅有1.41 m/s2，加速度波形不再显示出原行程时的冲击态，说明随着滑台行程的增大，悬浮架与车体间横向移动更加自由从而在运行过程中可以更加贴近轨道，减小了悬浮模块上滑橇与F轨之间的接触。

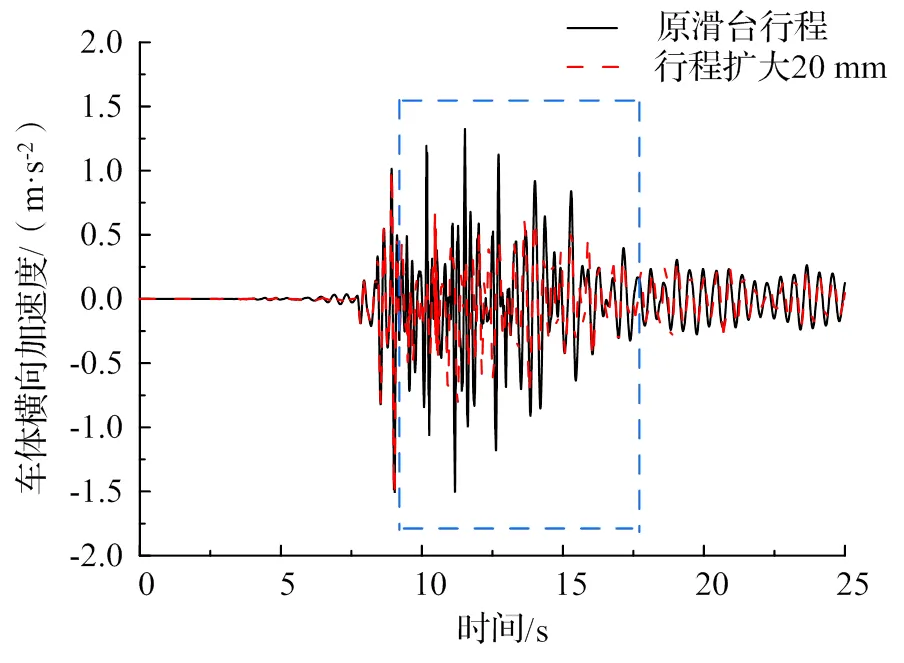
图10 车体前端横向加速度

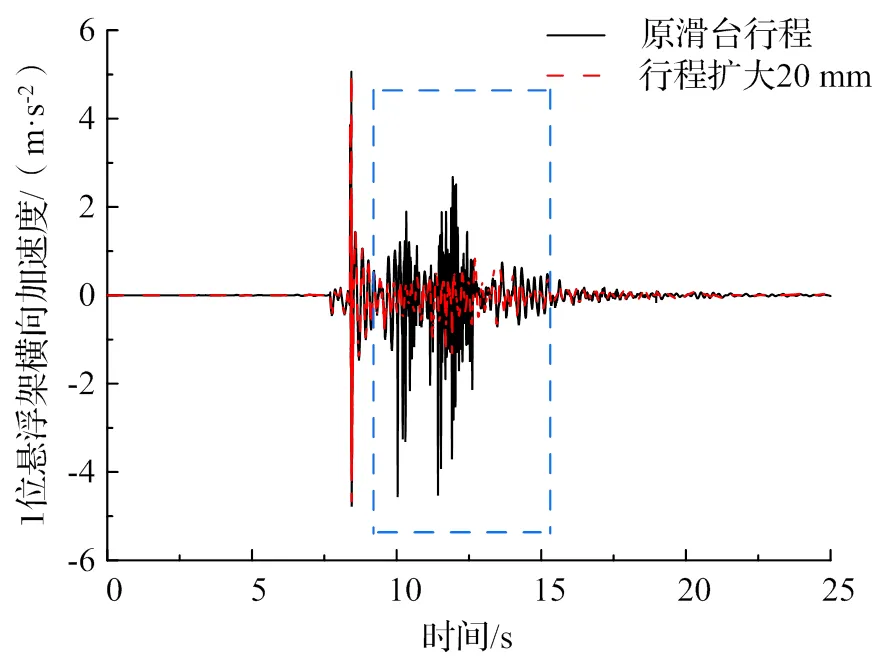
图11 悬浮架横向加速度

扩大滑台行程后悬浮架在运行中可以更贴近轨道，悬浮架的磁铁横移量会根据行程扩大量的不同而减少。图12为1位悬浮架电磁铁前端横移量的对比图，9.2 s后，横移量幅值由27.28 mm减小至21.03 mm，磁轨间机械接触的可能性变小，同时更少的横移量也更有利于悬浮控制系统的稳定，有利于提高行车安全性。

图13为滑台行程增加20 mm后主动梁跨中横向加速度与原行程时的对比曲线，滑台行程增加后，跨中处横向加速度幅值由4.10 m/s2减小至1.92 m/s2，道岔梁体受到来自悬浮架力的作用减小，同时冲击造成的加速度波形明显减少，说明扩大滑台行程可以有效减少道岔梁体受到的横向外力。考虑到原滑台行程与行程扩大后梁体横向位移很小，在此不再赘述。

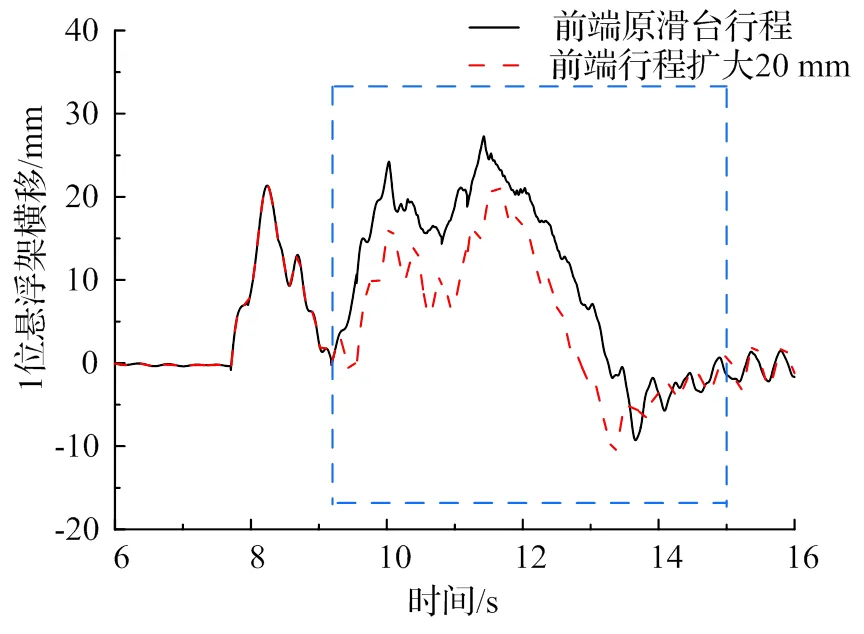
图12 磁铁最前端横移量变化对比

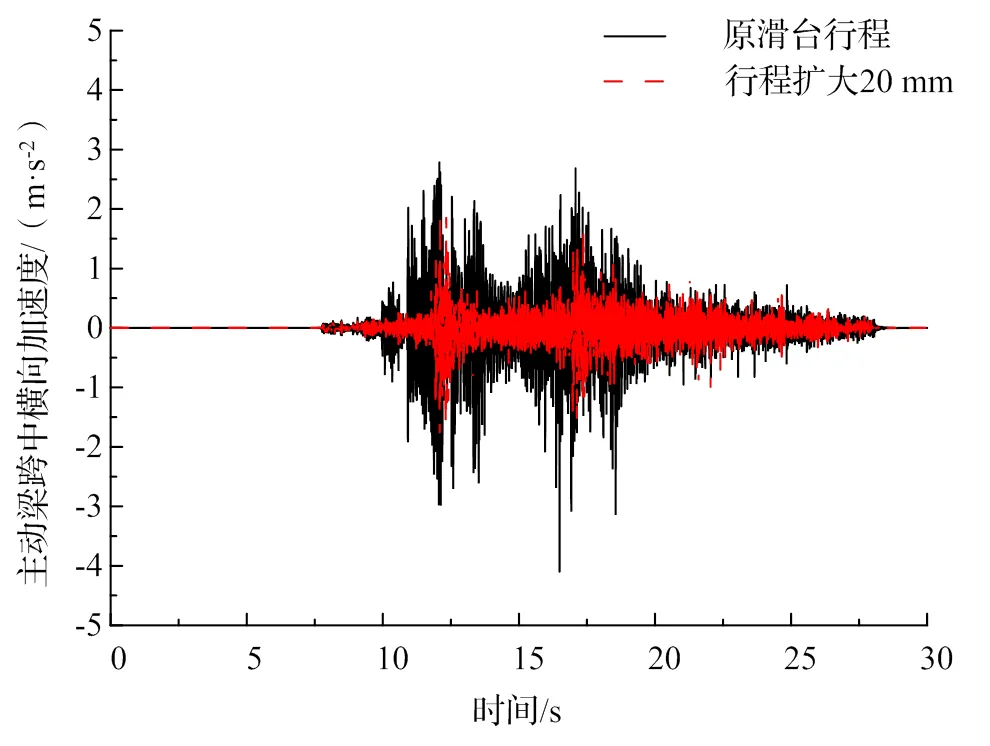
图13 主动梁跨中处横向加速度对比

4.2 滑台行程对系统动力学响应的影响规律

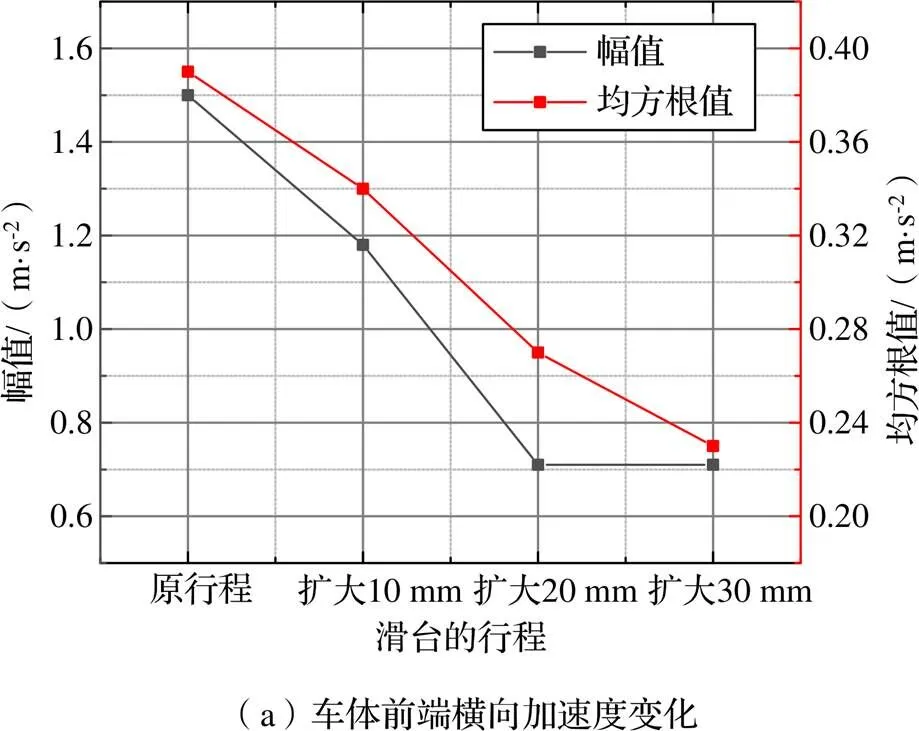
为了探究滑台行程对系统响应的影响规律，本小节给出了将滑台行程扩大10～30 mm时各动力学响应的变化趋势图。图14给出了随着滑台行程不断增大，车辆运行时间9.2 s后车体前端以及1位悬浮架横向加速度的幅值与均方根值统计。从图中可看出，二者均随滑台行程扩大明显减小，车体前端横向加速度幅值由1.50 m/s2减小至0.71 m/s2，均方根值由0.39 m/s2减小至0.23 m/s2；悬浮架横向加速度幅值与均方根值分别由4.54 m/s2、0.87 m/s2减小至 0.88 m/s2、0.31 m/s2，磁轨间机械接触概率减小。说明适当增加滑台行程可以有效减少车辆系统的横向振动。

随滑台行程的不断扩大，1位悬浮架最前端电磁铁横移量幅值变化如图15所示。当滑台行程扩大30 mm后，磁铁横移量幅值减小至16.58 mm，明显小于原滑台行程时的27.28 mm。由图可得，随着滑台行程的增加，磁轨间机械接触概率逐渐降低，悬浮控制系统由于磁铁横移量的减小而更加稳定。

图16给出了道岔主动梁跨中处横向加速度幅值随滑台行程不断扩大的变化规律，从图中可得，当滑台行程扩大30 mm时主动梁跨中处的横向加速度幅值由4.10 m/s2减小至1.77 m/s2，道岔梁横向响应明显减小。综上所述，从耦合动力学的角度出发，扩大滑台行程可以有效减少车－岔系统的横向响应，在工程实际中如果车下空间允许，可以适当增加滑台行程。

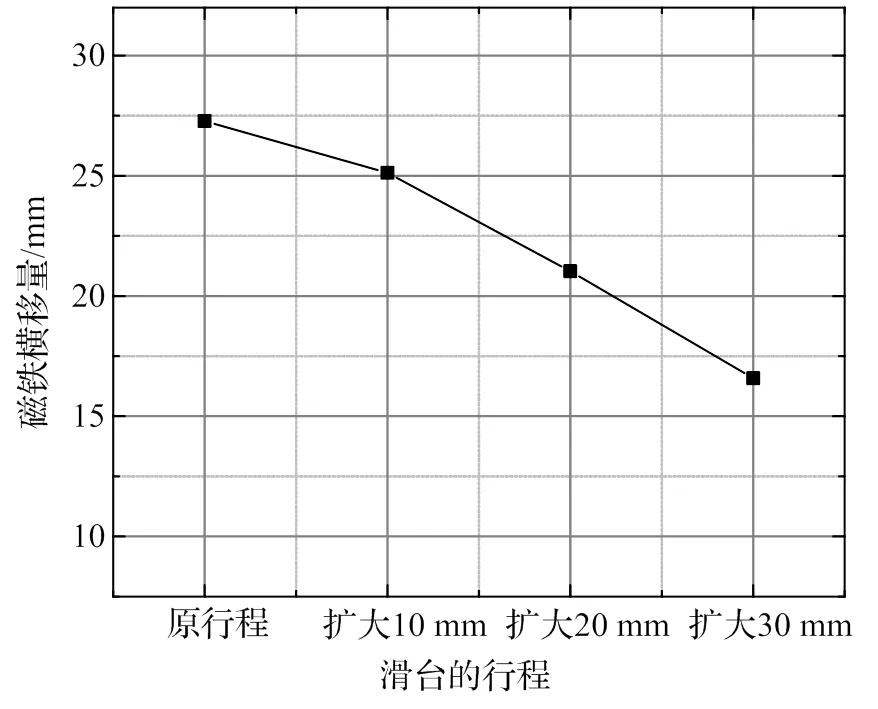
图15 滑台行程对磁铁横移量的影响规律

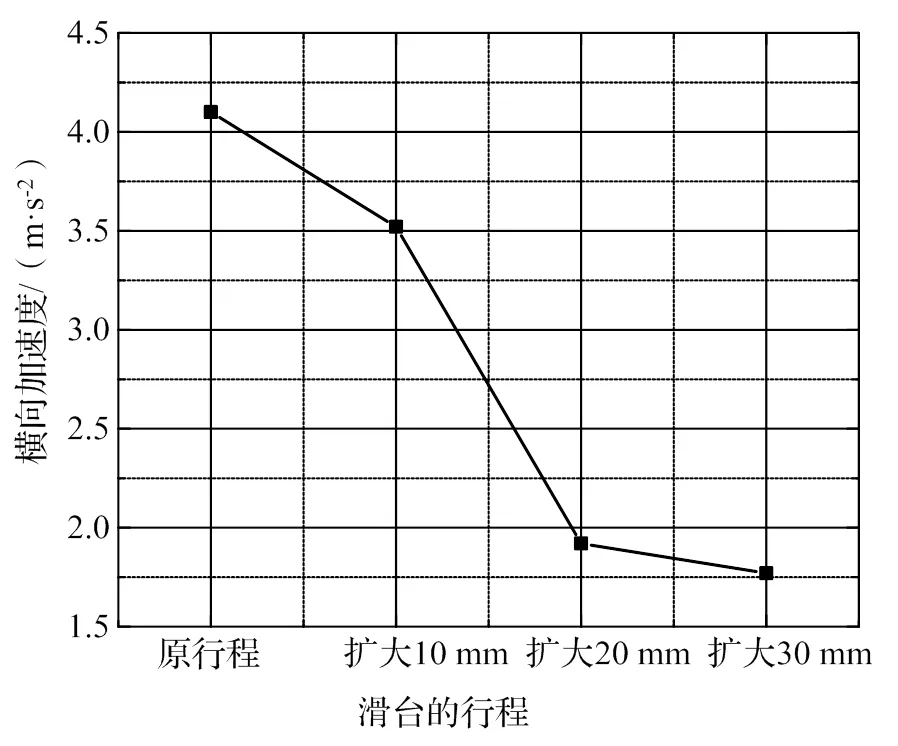
图16 滑台行程对主动梁横向加速度的影响规律

5 结论

本文建立了细致的侧向位道岔梁有限元模型及包含PID主动控制的中低速磁浮车辆动力学模型，采用长沙测试结果进行模型验证后，仿真分析了角平分装置以及滑动支承台行程对磁浮车辆通过侧向位道岔时系统动力学响应的影响，得到以下主要研究结论：

（1）角平分装置改变了道岔相接处F轨的相对转角，有效减小了磁浮车辆侧向过岔时的车—岔系统响应。取消角平分装置设置，车体前端横向加速度由1.50 m/s2增加至2.11 m/s2，接近GB/T 5599－2019[23]中对车体振动加速度限值2.5 m/s2的规定。同时悬浮架及道岔梁体的横向响应明显增大，可能会减少二者使用寿命并增加维护成本，严重时甚至会影响行车安全。

（2）滑台行程增加后减少了车体对于悬浮架的约束，滑台行程增大至30 mm时，车－岔系统的横向加速度明显减小，加速度波形中冲击作用逐渐减弱，电磁铁横移量由27.28 mm减小至16.58 mm，降低了发生磁轨间机械接触以及悬浮失稳的风险。

（3）从耦合动力学角度出发，综合考虑中低速磁浮车辆侧向通过道岔的动力学性能，实际工程应用中在道岔连接处设置角平分装置可以有效提高过岔时的平稳性与安全性，同时在车下空间等情况允许的条件下，可以适当增大滑台行程提高磁浮车辆侧向过岔性能。

[1]翟婉明，赵春发. 磁浮车辆/轨道系统动力学（Ⅰ）——磁/轨相互作用及稳定性[J]. 机械工程学报，2005，41（7）：1-10.

[2]翟婉明，赵春发. 现代轨道交通工程科技前沿与挑战[J]. 西南交通大学学报，2016，51（2）：209-226.

[3]徐飞，罗世辉，邓自刚. 磁悬浮轨道交通关键技术及全速度域应用研究[J]. 铁道学报，2019，41（3）：40-49.

[4]马卫华，罗世辉，张敏，等. 中低速磁浮车辆研究综述[J]. 交通运输工程学报，2021，21（1）：199-216.

[5]曾国锋，袁亦竑，吉文，等. 长沙中低速磁浮工程的道岔设计与调试[J]. 城市轨道交通研究，2016，19（5）：44-48.

[6]周文. 中低速磁浮道岔安装调试技术[J]. 铁道建筑技术，2020（5）：151-154+164.

[7]王红霞. 中低速磁浮道岔关键零件寿命及工艺研究[J]. 铁道标准设计，2017，61（10）：20-23.

[8]袁青平，王俊杰，王财华，等. 中低速磁浮交通道岔系统工程设计[J]. 都市快轨交通，2009，22（1）：67-70.

[9]LEE J M，HAN H S，KIM C H，et al. Status of development of the segmented 3 way Maglev switch and running tests[C]. Daejeon：Proceedings of the 21th International Conference on Magnetically Levitated Systems and Linear Drives （MAGLEV’2011），2011.

[10]SHIN H J，LEE J M，HAN H S，et al. Vibration test between Maglev vehicle and switching system[C]. Daejeon：Proceedings of the 21th International Conference on Magnetically Levitated Systems and Linear Drives （MAGLEV’2011），2011.

[11]杨奇科，程雄. 磁浮车辆－道岔振动特征分析[J]. 电力机车与城轨车辆，2016，39（5）：63-66.

[12]刘大玲. 中低速磁浮道岔动载试验方法研究[J]. 城市轨道交通研究，2017，20（5）：89-92.

[13]柴小鹏，汪正兴，王波，等. 磁浮工程道岔梁的TLMD减振技术研究[J]. 世界桥梁，2017，45（2）：60-65.

[14]靖仕元. 多重调谐质量调谐阻尼器的磁浮道岔减振方案[J]. 铁道工程学报，2019，36（4）：80-83，89.

[15]张宇生，赵春发，周文，等. 不同约束条件下中低速磁浮道岔主动梁自振特性[J]. 铁道标准设计，2020，64（4）：22-27.

[16]李苗. 中低速磁浮车辆－轻型道岔钢梁耦合振动研究[D]. 成都：西南交通大学，2018.

[17]夏书龙. 中低速磁浮车辆－道岔梁耦合振动仿真分析[D]. 成都：西南交通大学，2020

[18]刘东生. 悬浮控制算法及参数对中低速磁浮车辆－钢道岔梁耦合振动的影响分析[D]. 成都：西南交通大学，2021.

[19]杨志南，冯洋，刘东生，等. 悬浮控制参数对磁浮车辆与道岔梁耦合振动的影响分析[J]. 机械，2022，49（2）：38-46.

[20]谢海林. 中低速磁浮交通系统工程化应用—长沙磁浮快线[M]. 北京：中国铁道出版社，2018：23-35.

[21]BRrzezina W，Langerholc J. Lift and side forces on rectangular pole pieces in two dimensions[J]. Journal of Applied Physics，1974，45（4）：1869-1872.

[22]ZHAO Chunfa，ZHAI Wanming. Maglev vehicle/guideway vertical random response and ride quality[J]. Vehicle System Dynamics，2002，38（3）：185-210.

[23]国家市场监督管理总局，国家标准化管理委员会. 机车车辆动力学性能评定及试验鉴定规范. GB/T 5599－2019[S]. 北京：中国标准出版社，2019.

Analysis of Factors Affecting Dynamic Performance of Medium-Low Speed Maglev Vehicles When Passing Through the Switch of Branch Route

ZHAO Yifan，ZHAO Chunfa，PENG Yeye，FENG Yang

(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)

In order to investigate the influencing factors of dynamic performance of medium-low speed maglev vehicles when passing through the switch of branch route, the coupling dynamics model of medium-low speed maglev vehicle on the switch of branch route is established by using the UM software. In the vehicle dynamics model, the support platform, forced steering mechanism, lateral skid of the electromagnet and the PID suspension control system of active control are considered in detail. At the same time, the finite element model of the switch including the long-span girder, two short-span girders, angle bisector and F-rail is established. After the vehicle dynamics model is verified by the field measured data of Changsha maglev express, the effect of the angle bisector and the travel of the sliding support platform on the system dynamics response when the maglev vehicle is passing through the switch are compared and analyzed under the speed condition of 10km/h. The simulation results show that if the angle bisector is not set, the system response will increase and the amplitude of lateral acceleration at the front end of the vehicle body will increase by about 40%. After expanding the travel of the sliding support platform by 30mm, the lateral response of the system is significantly reduced, and the lateral displacement of electromagnet is reduced by 10.70mm, which can effectively avoid the mechanical contact of F-rail and suspension instability. Setting the angle bisector based on the comprehensive consideration of the dynamic performance of maglev vehicle when crossing the switch can effectively improve the stability and safety of vehicle operation. At the same time, if the actual situation allows, the travel of sliding support platform can be increased to further optimize the system response.

maglev train；joint switch；branch route；angle bisector；sliding support platform

U237；U213.6

A

10.3969/j.issn.1006-0316.2022.08.006

1006-0316 (2022) 08-0030-09

2022-03-04

国家重点研发计划项目子课题（2016YFB1200601）；湖南创新型省份建设专项（2020GK2084，2020GK2072）

赵逸凡（1997－），男，山东日照人，硕士研究生，主要研究方向为磁浮车辆—桥梁耦合动力学，E-mail：2487797822@qq.com。*通讯作者：赵春发（1973－），男，湖北仙桃人，博士，研究员，主要研究方向为轨道交通工程动力学，E-mail：fyswjtu@outlook.com。