基于改进智能驾驶员模型的车队纵横向协同控制

覃频频，张顺锋，吴锋民，谭鸿运，黄俊明

(1. 广西制造系统与先进制造技术重点实验室, 广西 南宁 530004； 2. 广西大学 机械工程学院, 广西 南宁 530004)

0 引言

智能网联汽车作为智能交通领域的重要组成部分，近年来已成为国内外各大研究院和车企的研究热点[1]。其中纵横向协同控制是智能网联汽车实现自动驾驶的关键技术之一[2]，由于车辆是高度非线性、强耦合的时变系统，独立进行纵向或横向控制将可能导致整车性能冲突，降低控制系统精度和安全性[3]。因此在保证行驶安全性、舒适性和平顺性等前提下，如何有效利用车辆纵横向关联特性，实现对智能网联汽车组成的车队的纵横向协调控制，还需要进一步研究。

Bayuwindra等[4]针对智能网联车队纵横向协同控制设计了基于协同自适应巡航的纵横向非线性控制器，该控制器通过雷达和Vehicle to Vehicle (V2V)获取引导车辆速度和航向信息，实现车队基于纵向安全距离的跟驰行驶，且能够补偿车队中的急转向行为。Chen等[5]提出了一种分层混合控制系统，该系统高层根据周围车辆状态做出安全的驾驶行为决策，低层采用模型预测控制方法整合车辆纵向和横向控制。Tork等[6]提出了一种基于改进的自适应神经控制器的模型独立控制方法，通过转向角和扭矩的输入实现了纵横向运动的协同控制。梁艺潇等[7]采用神经网络逆系统与内模控制器结合的解耦控制策略实现了汽车纵横向运动之间的解耦，并通过反馈调节进一步提升控制系统性能，使其在各种输入条件下都能良好跟踪期望速度和横摆角速度。谢辉等[3]提出了一种基于模型预测控制的纵横向协同控制方法，该方法将当前车辆系统状态与纵向速度预测序列输入横向控制器，实现车辆速度与路径的有效控制。李军等[8]考虑路面地形因素提出了一种基于Proportion Integral Differential (PID)和模型预测控制的纵横向协同控制方法，该方法有效减少了路径跟踪误差，且改善了车辆的行驶稳定性。

以上研究虽然考虑了车辆纵横向运动耦合特性，但未考虑弯道、超高和坡度等道路几何设计参数对协同控制的影响。为此，设计基于改进智能驾驶员模型与单点预瞄模型相结合的纵横向协同控制系统，并在Carsim/Simulink联合仿真平台中设置加减速、双移线和匝道工况验证该系统的协同控制性能。

1 纵向跟驰控制系统

对智能网联环境下的车队跟驰车辆，基于车联网技术获取道路参数和车辆相关行驶信息[9]，并传递给纵向跟驰控制系统的上层加速度模型求解期望加速度，随后下层逆纵向动力学模型根据接受的上层加速度信息，协调控制发动机节气门开度与制动压力，最终实现对引导车辆的纵向跟驰行驶。

1.1 上层加速度控制模型

IDM模型是2002年Helbing[10]在大量试验基础上，结合以往经典交通流跟驰模型而提出的广义力模型。该模型中参数较少，且均有明确意义[11]，是目前最完整、最简单、无事故的跟驰理论模型，故可应用于车辆纵向跟驰控制。道路设计是为车辆提供高效、舒适和安全的行车环境[12]，因此针对实际道路工况，考虑弯道、超高及坡度等道路几何设计参数对跟驰行为的影响，得到IIDM模型[13]：

(1)

(2)

式中，ades为IIDM模型产生的期望加速度；aACC为由IDM模型产生的Adaptive Cruise Control(ACC)加速度；R0为弯道上车辆最小转弯半径；η为与R0相关的常数；R为道路曲率半径；g为重力加速度；ih为道路坡度值；Vd为弯道设计时速；μ为横向力系数；ie为道路超高值。

1.2 下层逆纵向动力学模型

下层逆纵向动力学模型包括逆发动机与逆制动系统模型。据图1逆发动机特性曲面建立逆发动机模型。

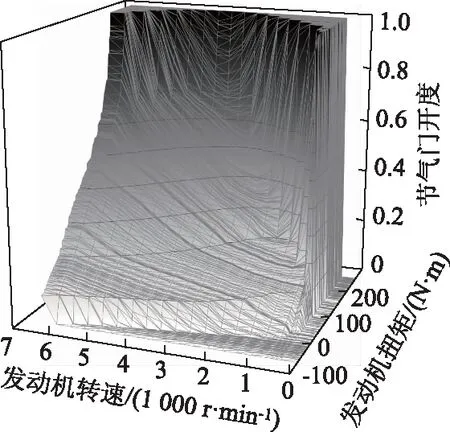
图1 逆发动机特性曲面Fig.1 Curved surface of inverse engine characteristics

当车辆处于驱动工况时，由期望加速度计算发动机输出扭矩和转速，并通过逆向查表获得期望节气门开度[14]：

αdes=MAP-1(ωe,Te)，

(3)

式中，αdes为期望节气门开度；ωc为发动机转速；Te为发动机转矩。

当车辆处于制动工况时，发动机驱动力为0，车辆受力由汽车行驶平衡方程式简化为：

mades=-Fxb-(Ff+Fω)，

(4)

式中，m为车辆质量；Fxb为车辆制动力；Ff和Fω为滚动阻力与空气阻力。

车辆在制动力限值范围内，其制动力与制动压力可视为线性正相关[15]。由逆制动系统模型计算期望制动压力：

(5)

式中，Pdes为期望制动压力；Kb为比例系数。

2 横向轨迹控制系统

2.1 单点预瞄模型

假设驾驶员具有一定的轨迹预测能力，且在1个预瞄时间内车辆保持恒定的纵向车速与横摆角速度[16]。基于上述假设，如图2所示，车辆作以M为圆心、Ra为半径的匀速圆周运动，其中θ为圆弧轨迹所对应的圆心角。

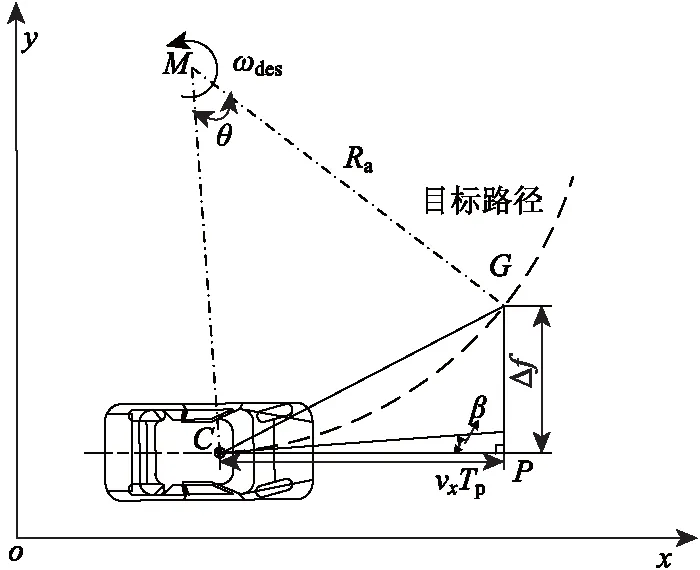
图2 单点预瞄模型Fig.2 Simple-point preview model

由车辆动力学理论分析，可知横摆角速度对转向角的稳态响应Gω为：

(6)

(7)

式中，vx为车辆质心处纵向速度；isw为转向系传动比；L为轴距；Lf和Lr为质心到前、后轴的距离；K为车辆稳定性系数；K1和K2分别为前、后轮侧偏刚度。

单点预瞄模型先根据横向预瞄偏差决策出期望转向角，再由车辆行驶过程中所感知的车辆状态对转向角进行反馈控制[17]：

(8)

(9)

式中，δf为滑模控制率；ωdes为期望横摆角速度；Δf为横向预瞄偏差；Tp为预瞄时间；β为质心侧偏角；δdes为期望转向角；Δδ为反馈控制转向角；ω为实际横摆角速度；Kω为反馈系数。考虑车辆处于稳态，取名义值为Gω。

2.2 滑模控制器

为提高轨迹跟踪精度，在原模型基础上设计滑模控制器代替反馈控制。选取实际与理想横摆角速度之差为控制量：

e=ω-ωdes。

(10)

定义切换函数为:

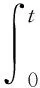
(11)

式中λ为正的加权系数。

δf=δeq-φ·sgn(s)，

(12)

(13)

式中，δeq为等效控制输入；φ为系统的运动点趋近滑模切换面的速率，且需要满足式(14)；Iz为整车绕z轴的转动惯量；sgn(·)为符号函数。

(14)

式中σ为正实数。

为进一步消除滑模控制输入的高频振动，改善控制性能，采用饱和函数替换符号函数[19]：

(15)

综上，最终滑模控制率为：

δf=δeq-φ·sat(s/ε)，

(16)

式中ε为边界层厚度。

3 仿真验证

3.1 纵横向协同控制系统参数选取

以纵向跟驰控制系统的输出速度为耦合变量，输入横向轨迹控制系统中，以此建立如图3所示的纵横向协同控制系统。

图3 纵横向协同控制系统Fig.3 Longitudinal and lateral coordinated control system

搭建Carsim/Simulink联合仿真平台，采用加减速、双移线和匝道工况验证该系统控制性能。其主要参数如表1所示。

表1 协同控制系统主要参数Tab.1 Main parameters of coordinated control system

3.2 加减速工况

设置道路摩擦系数0.85，各车初始行车间距5 m。引导车辆以10 km/h初速度在80 s内完成一段匀加速、匀速和匀减速行驶。仿真结果如图4所示。从图4 (a)～(b)可看出，跟驰车辆皆对引导车辆速度和加速度保持较高的跟随精度，且消除了引导车辆加速度的剧烈变化，提高了乘坐舒适性。从图4 (c)可看出，行车间距在跟驰过程中与速度呈正相关，且当速度稳定为100 km/h时其趋向于31.42 m并保持稳定。综上说明该协同控制系统具有良好的纵向跟驰性能。

图4 加减速工况Fig.4 Acceleration-deceleration conditions

3.3 双移线工况

设置道路摩擦系数0.85，总长250 m的双移线工况，分别采用Carsim内置的预瞄最优模型，和本研究基于反馈控制与滑膜控制的2种单点预瞄模型组成的协同控制系统，进行车速为40 km/h的仿真试验，仿真结果如图5所示。从图5(a)可看出，2种控制系统转向角与Carsim模型皆有较好的一致性且转向平滑，其中滑膜控制的转向角一致性更高。从图 5 (b)～(c)可看出，2种控制系统皆具有较高的横向轨迹跟踪精度，侧向偏移量皆小于0.2 m，其中滑膜控制的轨迹更接近理想轨迹。综上说明,该协同控制系统具有较高的横向轨迹跟踪精度，且滑膜控制的跟踪精度比反馈控制更高。

图5 双移线工况Fig.5 Double shifting line conditions

3.4 匝道工况

设置道路摩擦系数0.85，弯道半径180 m，超高和坡度皆为2%的匝道，各车初始行车间距为19 m，车辆初速度60 km/h，匝道设计时速40 km/h。其中跟驰车辆分别采用基于IDM与IIDM模型搭建的纵横向协同控制系统。仿真结果如图6所示。可以看出，由2种控制系统所组成的智能网联车队整体都表现出了良好的纵向跟驰性能和较高的横向轨迹跟踪精度。从图6 (b)～(c)可看出，驶入匝道时IIDM跟驰车辆比IDM跟驰车辆具有更大减速行为，且在匝道行驶过程中具有更大行车间距，其中IIDM跟驰车辆行车间距为14.16 m，比IDM跟驰车辆增加了0.55 m。从图6 (d)可看出，2种系统的转向角与引导车辆基本保持一致，但由于匝道出入口处超高存在突变，使车辆侧倾状态变化，导致车队整体转向角出现略微波动，同时由于车辆纵向速度变化存在耦合性，导致IIDM跟驰车辆转向角略小于IDM跟驰车辆。

图6 匝道工况Fig.6 Ramp conditions

从图6(e)可看出，转向角变化使得IIDM跟驰车辆平均侧向偏移比IDM跟驰车辆小2.51×10-6m，同时转向角波动导致侧向偏移量出现略微波动，但最大值皆小于0.03 m，属于安全范围。综上说明,基于IIDM模型所设计的协同控制系统在纵横向运动控制上的表现皆优于IDM模型。

4 结论

考虑车辆纵横向运动耦合特性，以纵向速度为耦合变量搭建了基于改进智能驾驶员模型与单点预瞄模型的纵横向协同控制系统，研究道路几何设计参数对智能网联车队纵横向协同控制的影响，有效实现了智能网联车队的纵横向协同控制。加减速、双移线和匝道工况下的仿真试验表明，建立的协同控制系统有良好的纵横向及其协同控制性能，能够较好地实现对引导车辆纵向跟驰行驶和横向轨迹跟踪。采用IIDM的协同控制系统对弯道、超高和坡度等道路几何设计参数的纵横向运动响应比IDM的控制系统更显著，且控制性能更优异，更有利于车队整体行驶安全性。

在研究纵向跟驰行为时采用了改进智能驾驶员模型，仅考虑了引导车辆的行驶信息，未考虑实际交通环境中多前车对跟驰行为的影响。同时在研究横向轨迹跟踪时采用单点预瞄模型，仅考虑了车辆前方单点的预瞄信息，未考虑实际决策过程中驾驶员往往会结合远近2点的道路预瞄信息。故未来可进一步考虑多前车的行驶信息和远近2点的预瞄信息对纵横向协同控制系统进行改进，从而更全面地反映驾驶员操纵车辆的真实行驶情况。