早强低收缩混凝土早期收缩性能及预测模型
2022-09-28王吉坤占玉林贾银钧荆国强
沈 东,王吉坤,占玉林,贾银钧,荆国强
(1. 温州市七都大桥北汊桥建设有限公司,浙江 温州 325099;2. 西南交通大学 土木工程学院,四川 成都 610031;3. 中铁大桥科学研究院有限公司,湖北 武汉 430034;4. 桥梁结构健康与安全国家重点实验室,湖北 武汉 430034)
0 引言
普通混凝土材料具有抗拉强度低、收缩大的特点。为减小混凝土的自收缩,从而改善混凝土的收缩开裂问题,越来越多的桥梁在用料上开始向混凝土中掺入钢纤维或玄武岩纤维,用来改善其抗拉性能[1]及收缩性能[2]。
在钢-混凝土组合结构中,混凝土板内部均会密布钢筋、钢板以及栓钉等约束,这类钢材类骨架均会导致混凝土在收缩过程中受到严重的限制,使混凝土结构产生约束收缩应力,导致混凝土早期存在较大的开裂风险。钢-混组合结构中,混凝土自收缩在受到钢筋、栓钉等内约束时,会产生较大的拉应力[3]。上述由于自收缩受到约束而导致混凝土构件的开裂荷载和拉伸刚度[4]的降低均可能对结构的实际使用造成不利影响,为了解决这些问题,需要对混凝土早期收缩进行研究。
为了防止混凝土在早期因收缩而开裂,一方面要研究混凝土自身的力学性能以及收缩行为,另一方面还要研究约束条件对混凝土收缩的影响。周胜波等[5]通过改变用水量和水泥用量研究了水灰比对混凝土自收缩的影响,研究发现水灰比下降会使收缩增加,且小于100 nm的毛细孔对自收缩起关键作用。Lura等[6]针对养护条件和水泥种类两个因素进行混凝土早期自由收缩试验,结果显示,养护温度的提升不会导致混凝土收缩值变大,但往往会加快其收缩发展速度;在其余条件一致的情况下,使用矿渣水泥的混凝土收缩明显比使用波特兰水泥的大。同样的发现也被Zhang等[7]证明。杨进等[8]探究了不同类型减缩剂对混凝土早期收缩的影响,试验表明,在密封养护条件下吸水树脂SAP和膨胀剂能有效减小混凝土收缩,而干燥养护条件下有机减缩剂能较好地减小混凝土收缩。Branston等[9]研究了玄武岩纤维对自由和约束塑性收缩的影响,发现玄武岩纤维能有效降低自由收缩的幅度,以及通过限制裂纹生长(如果裂纹确实发生的话)有效地防止了裂纹发展。华建民等[10]研究了栓钉对高强混凝土约束收缩的影响,结果显示,混凝土约束收缩因约束度的增加而减小,并发现了栓钉约束最优组合。
目前研究主要集中在各类结构中混凝土的约束收缩效应上,且均以试验为主,旨在得出各因素对约束收缩效应的影响。但从实际结构的约束收缩预测角度出发,相关研究则较少,要合理地预测结构的约束收缩行为,则需建立混凝土的自由收缩模型,并在此基础上提出合理的约束收缩分析模型。
本研究通过试验测得一种早强低收缩玄武岩纤维混凝土的力学性能与早期自由收缩。首先对其早期性能进行分析,再利用现有国内外常用的收缩预测模型进行估算并与实测值对比分析;然后,在详细研究已有预测模型的基础上,考虑玄武岩纤维掺量对预测模型进行修正,得到早强低收缩玄武岩纤维混凝土的自由收缩预测模型;最后,提出了钢-混组合结构的约束收缩计算模型,并设计了早强低收缩玄武岩纤维混凝土约束收缩试验,验证了所提出的自由收缩模型以及约束收缩分析模型的正确性。
1 收缩预测模型
混凝土的收缩性能是影响混凝土开裂的重要因素之一,随着其被发现,国内外学者开展了大量的试验研究。由于收缩作用受到的影响因素众多,对每一种配比的混凝土以及在不同条件下的收缩进行试验极其不现实,因此选取合适的收缩预测模型对混凝土在各类因素影响下的收缩进行合理估算显得尤为重要。目前国内外常见的收缩估算公式都是建立在试验和扩散理论的半经验公式基础上,通常都为收缩随龄期的发展函数乘以若干个修正系数,各类模型之间的差异往往是发展函数的不同,以及包含的影响因素取值和种类的不同,其中较具有代表性的有以下几种:ACI模型[11]、CEB-FIP模型[12]、GL2000模型[13]以及王铁梦模型[14]等。
(1)ACI209模型
由美国混凝土协会(ACI)提出,采用101.6 mm×101.6 mm×285.75 mm的混凝土棱柱体试件,测量存放于相对湿度40%、温度20 ℃环境中棱柱体的收缩,其表达式如下:

(1)
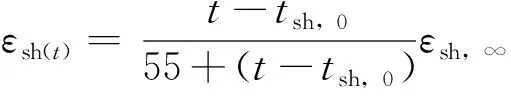
(2)
εsh,∞=780γsh·10-6,
(3)
式中,εsh(t)为混凝土的收缩应变;t为混凝土龄期;tsh,0为混凝土开始干燥的龄期;εsh,∞为混凝土最终的收缩应变;γsh为修正系数(包括干燥前养护时间、湿度、试件的体积、比表面积、砂率、单位水泥量、含气量影响等)。
(2)CEB-FIP模型
该模型由欧洲混凝土协会与国际预应力混凝土协会提出。如今我国桥梁规范的收缩预测便是采用该模型,其表达式如下:
εcs(t,ts)=εcs0βs(t,ts),
(4)
(5)
εcs0=βRH[160+10βsc(9-0.1fc28)]·10-6,
(6)
(7)
式中,εcs(t,ts)为素混凝土构件在未加载情况下的平均收缩应变;ts为开始收缩时的混凝土龄期;εcs0为混凝土收缩应变修正系数;βs(t,ts)为收缩应变随时间变化的系数;Ac为构件的横截面面积;u为与大气接触的截面周界长度;βRH为相对湿度修正系数,取决于环境的相对湿度RH;βsc为水泥种类修正系数,取决于水泥品种;fc28为混凝土的圆柱体抗压强度。
(3)GL2000模型
1999年美国混凝土协会提出了混凝土收缩预测模型的建立准则,2000年Gardner N.J和Lockman M.J在该准则的基础上对GZ模型进行修正,提出了GL2000模型,其表达式如下:
εsh=εshuβ(h)β(t),
(8)
(9)
β(h)=1-1.18h4,
(10)
(11)
式中,εsh为混凝土收缩应变;εshu为混凝土的收缩终值;β(h)为相对湿度发展函数;β(t)为龄期发展函数;K为与水泥类型有关的系数;fcm28为混凝土龄期为28 d时的圆柱体抗压强度平均值;V/S为混凝土构件的体表比;h为环境相对湿度;tc为混凝土开始干燥时的龄期。
(4)王铁梦模型
我国著名工程结构裂缝控制专家王铁梦在1 220次收缩试验数据的基础上,结合国内实际,归纳出适合国内工程的混凝土自由收缩模型。其基本思想与ACI规范一致,均以标准状态下混凝土的最终收缩值为基础,通过各种影响系数进行修正,再乘以时间发展函数,其表达式如下:
ε(t)=3.24·10-4·(1-e-0.01t)M1M2…Mn,
(12)
式中,ε(t)为混凝土收缩应变;M1,M2,Mn为各种非标准条件的修正系数(如水泥品种、水灰比、养护条件等情况)。
2 预测模型与自由收缩试验对比
2.1 自由收缩试验
早强低收缩玄武岩纤维混凝土设计强度为C60级混凝土,其配合比如表1所示。其中外加剂采用聚羧酸减水剂,减水率为16.2%;玄武岩纤维掺量采用工程中常见的0.3%。

表1 混凝土配比Tab.1 Proportion of concrete
自由收缩试验采用非接触式收缩变形测定仪进行试验,共制作3个试件,试验的模具尺寸为100 mm×100 mm×515 mm,在浇注并振捣密实后放置于实验室环境中(温度(20±2) ℃,相对湿度(60±5)%)进行养护,如图1所示。养护1 d后,安装测试设备,测量混凝土的自由收缩。在测试的28 d内,每天读取一次试验数据,并记录该时刻的温度与湿度。

图1 自由收缩试验Fig.1 Free shrinkage test
早强低收缩玄武岩纤维混凝土的力学性能试验严格按照规范进行,分别在第3,7,28 d龄期时,进行立方体抗压强度试验、立方体劈裂抗拉强度试验和棱柱体受压弹性模量试验,测定其各项基本力学性能。早强低收缩玄武岩纤维混凝土各项基本力学性能随龄期的发展如表2所示。
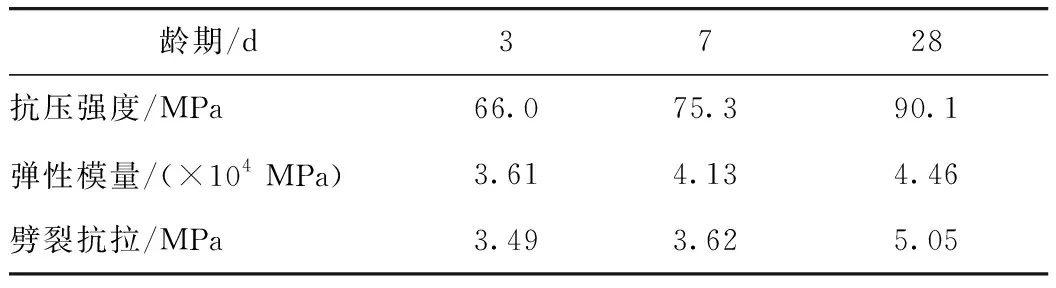
表2 混凝土力学性能Tab.2 Mechanical properties of concrete
早龄期自由收缩测试结果如图2所示。从图中可以看出,早期混凝土的收缩基本趋势为前期发展较快,中期速度放缓,后期发展趋于平稳,这是由于早期混凝土还处在发展阶段,水化反应以及水分蒸发均较为剧烈,同时自身弹性模量还未发展完全,使得早期变形速率较快;随着龄期不断增加,水化反应逐渐减弱,混凝土逐渐发育成熟,收缩速率自然逐渐稳定,这与目前已有的混凝土早期收缩特性研究结果一致。同时,根据相关文献[15-17],普通C60混凝土的早期自由收缩28 d的收缩率普遍在450以上,大于本试验中的342.8×10-6,说明本试验中的早强低收缩玄武岩纤维混凝土具有较好的早期收缩性能,可以有效降低混凝土结构早期收缩开裂的风险。

图2 早期自由收缩率Fig.2 Early free shrinkage rate
2.2 收缩预测模型对比
利用第1节中所述4类预测模型对早强低收缩玄武岩纤维混凝土的收缩进行估算,基于此来评估既有混凝土收缩模型对于早强低收缩玄武岩纤维混凝土的适用性,计算结果如图3所示。

图3 收缩预测模型估算曲线与实测数据的对比Fig.3 Comparison between estimation curve of shrinkage prediction model and measured data
由图3可知,上述4种模型对早强低收缩玄武岩纤维混凝土的收缩预测均有不同程度的误差。其中ACI209模型与王铁梦模型的估算效果最差,两种模型的基本思想一致,均是规定了标准条件下混凝土收缩的最终值,通过一系列相关因素的修正系数对不同条件下的收缩进行修正,每个时刻的收缩值通过乘以发展函数来得到。根据结果,上述两种模型的发展函数不适用于早强低收缩玄武岩纤维混凝土,因其低估了早期收缩发展速率。其余两种模型整体趋势与实测结果较为接近,均体现为早期收缩速率快,且早期收缩量在28 d收缩中占比较大。随着龄期增加,两种模型的收缩速率明显下降,28 d收缩值比实测值小19%左右。
综上所述,对于早强低收缩玄武岩纤维混凝土,4种国内外常用模型表现不一且均低估了其收缩值,其中ACI209模型与王铁梦模型不适用于预测早强低收缩玄武岩纤维混凝土,CEB-FIP模型与GL2000模型虽然也低估了早期自由收缩,但整体趋势与实测结果较为接近。
2.3 基于GL2000收缩模型的修正
针对早强低收缩玄武岩纤维混凝土的早期收缩性能,虽然CEB-FIP模型在整体趋势上与之相似,但早期收缩发展趋势过快,故以上述预测结果表现较好的GL2000模型为基础进行一定的修正,使得修正后的模型对早强低收缩玄武岩纤维混凝土的早期收缩有较好的适用性和准确性。从估算结果可以看出,GL2000模型在收缩初期和实测值有较好的吻合度,随着龄期发展,逐渐低估,因此保证环境相对湿度函数及收缩终值函数不变,通过对龄期发展函数设置修正系数来对收缩模型进行修正。修正后的龄期发展函数如式(13)所示:
(13)
式中,a,b均为待确定的修正系数。
将试件实测数据分别代入式(9)、式(10)及修正的β(t)中,通过与实测收缩值拟合即可得到修正后的参数分别为a=0.66和b=0.61,相关系数为R2=0.985,拟合后的自由收缩公式具体为:
(14)
式中,t为混凝土龄期。
收缩拟合曲线见图4,表明拟合公式与实测值有较高的吻合度。
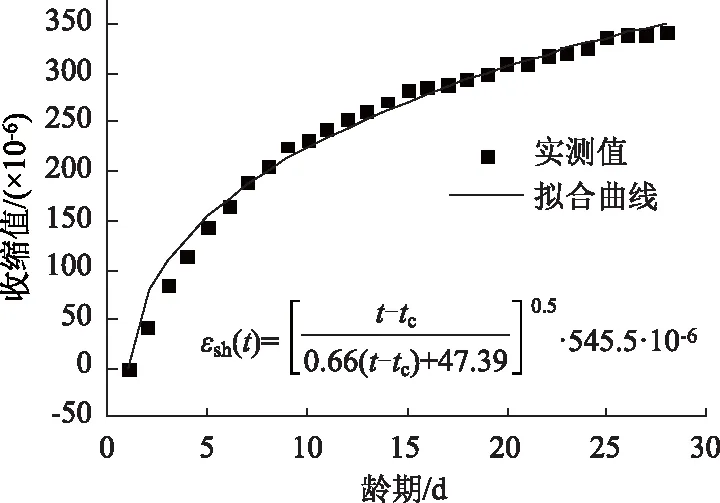
图4 收缩拟合曲线Fig.4 Shrinkage fitting curve
3 玄武岩纤维掺量影响分析
与普通混凝土相比,早强低收缩混凝土不仅在水灰比、外加剂等方面有所不同,同时还掺加了玄武岩纤维来提升其早期性能。纤维的加入能够在一定程度上缓解混凝土内部的应力集中,控制微裂缝的发展,使混凝土更具有韧性[18],并且能在一定程度上抑制混凝土早期收缩。现有的常用收缩模型均未考虑纤维掺量这个因素对于早期收缩的影响。为了探究纤维掺量对于早强低收缩混凝土早期自由收缩性能的影响,进行了不同纤维掺量的自由收缩试验,基于试验结果对上述模型进行进一步修正,为早强低收缩玄武岩纤维混凝土的自由收缩计算与分析提供一定参考。
3.1 玄武岩纤维掺量对自由收缩的影响
为研究玄武岩纤维掺量对自由收缩的影响,以0.30%体积掺量的混凝土为对照组,增设了4组试验,分别为0%,0.15%,0.45%,0.60%。不同纤维掺量混凝土28 d龄期的收缩发展曲线如图5所示。

图5 不同玄武岩纤维掺量下收缩随龄期变化曲线Fig.5 Curves of shrinkage varying with age under different basalt fiber contents
由图5可知,无论纤维掺量为多少,随着龄期增加,5组混凝土的自由收缩均呈现不断增长的趋势,并且增长速率在早期较快,中期放缓,后期趋于稳定,这说明纤维的掺入并不会改变混凝土本身的收缩规律。当早强低收缩混凝土没有掺入玄武岩纤维时,即体积掺量为0时,其28 d龄期内的收缩量均大于掺有纤维的混凝土,说明玄武岩纤维的掺入能够减小混凝土早期的自由收缩。这是由于纤维的加入会无规律地分布于混凝土内部,这种随机的、错杂的排列会有效减小内部骨料的沉降。一方面,纤维可以改变内部的孔隙结构,使得大孔径毛细孔的数量变多,能够有效减弱因水分流失而产生的毛细管压力;另一方面,纤维的加入会堵塞混凝土内部的渗水通道,同时由于玄武岩纤维具有一定的吸水性和保水性,能在一定程度上减少水分流失,降低混凝土与环境间的水分交换速率,从而达到减小早期收缩的作用[19]。
玄武岩纤维掺量对早期收缩的影响如图6所示。由图6可知,掺入玄武岩纤维能够明显减小混凝土7 d内的早期收缩,玄武岩掺量为0.15%,0.30%,0.45%,0.60%时分别比掺量为0%的混凝土收缩减小了24.2%,29.4%,35.6%,44.1%,有效地降低了混凝土早期开裂风险。对于不同龄期,纤维掺量的增多会减小早强低收缩混凝土的早期收缩,但需注意随着纤维掺量不断增多,混凝土内部界面不断增多,纤维均匀分布会逐渐困难。

图6 收缩值与玄武岩纤维掺量的相对关系Fig.6 Relationship between shrinkage value and basalt fiber content
3.2 基于纤维掺量的早强低收缩混凝土收缩预测模型
基于上述纤维掺量对早强低收缩混凝土收缩的分析,对第2章中的模型进行一定的修正,通过引入纤维相关的参数βf来实现修正。基于3.1节中,考虑到纤维掺量对混凝土收缩抑制效果的复杂性,采用二次函数的形式来考虑,修正后的公式如下:
εsh-f(t)=εsh(t)·βf,
(15)
βf=c+d(vf-0.003)+f(vf-0.003)2,
(16)
式中,εsh-f(t)为考虑纤维修正后混凝土的收缩应变;εsh(t)见式(14);βf为纤维影响系数;c,d,f均为待定常数;vf为纤维掺量。
通过收缩试验数据对上述公式进行拟合,得到待定的常数为c=0.99,d=-59.71,f=5 938,各组数据的相关系数均在0.93以上。修正后的早强低收缩玄武岩纤维混凝土收缩预测模型为:
βf·10-6,
(17)
βf=0.99-59.71(vf-0.003)+5 938(vf-
0.003)2。
(18)
基于玄武岩掺量的早强低收缩混凝土自由收缩值及拟合值对比如图7所示。由图7可知,基于GL2000收缩预测模型的修正模型能够较好地预测早强低收缩玄武岩纤维混凝土的早期收缩。
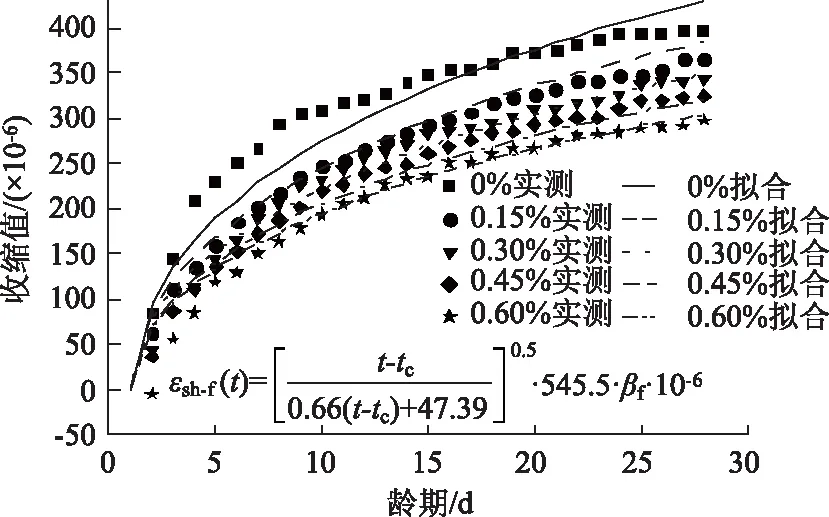
图7 收缩实测值及拟合值的对比Fig.7 Comparison of measured values with fitted values of shrinkage
4 自由收缩预测模型在钢-混组合结构中的适用性
为验证早强低收缩玄武岩纤维混凝土自由收缩预测模型的正确性,建立了约束收缩计算模型,并结合所提出的自由收缩预测模型预测了钢-混组合结构的约束收缩,最后与试验结果进行了对比。
设计使用早强低收缩玄武岩纤维混凝土进行栓钉的轴向约束试验,如图8所示。整体试件尺寸为160 mm×150 mm×400 mm的长方体,其中,混凝土部分采用150 mm×150 mm×400 mm的长方体,下设10 mm×150 mm×400 mm的钢板,两者通过栓钉有效连接。其中混凝土配合比同表1,钢板采用Q235型钢板,栓钉采用ML15AL材质的圆柱头焊钉。采用正交试验的方法设计了9组试验,综合考虑了栓钉的直径、高度和间距对早强低收缩玄武岩纤维混凝土约束收缩的影响,如表3所示。
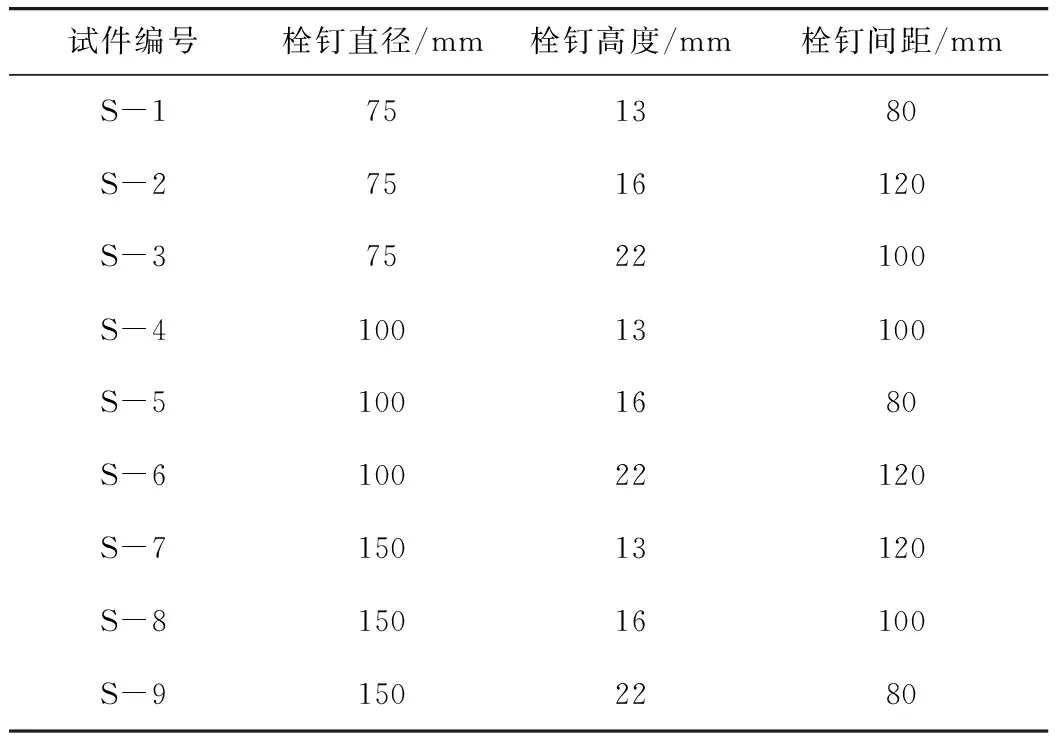
表3 试验方案Tab.3 Test scheme

图8 栓钉轴向约束收缩试验Fig.8 Axial restraint shrinkage test on stud
在上述试验基础上,对混凝土的约束收缩采用有限元分析软件ABAQUS建立了有限元模型,模型尺寸与试验尺寸一致,如图9所示。混凝土、栓钉及钢板采用弹塑性双折线模型。混凝土、栓钉和钢板均采用8节点的三维实体线性减缩积分单元(C3D8R)。钢板和混凝土之间、栓钉的上、下表面与混凝土之间的接触采用切向无摩擦、法向擦硬接触,不考虑钢板和混凝土接触面的粘结作用。栓钉侧面与混凝土的接触采用切线方向的罚函数列式和法线方向的硬接触。

图9 有限元分析模型Fig.9 Finite element analysis model
对于混凝土收缩的模拟,通过“当量温差法”实现,将混凝土每天的自由收缩应变值ε(t)通过热膨胀系数αc换算为当天的温度,并将温度荷载施加在模型上。
对比28 d的实测和模拟的约束收缩应变,可见误差都在10%以内,如表4所示,说明早强低收缩玄武岩纤维混凝土约束收缩有限元模型与现场实测约束收缩吻合度很高,该模型能够准确模拟有栓钉的混凝土约束收缩。

表4 28 d的约束收缩应变实测值与模拟值的对比Tab.4 Comparison of measured values and simulated values of constrained shrinkage strain in 28 d
基于布置单排栓钉的轴向约束收缩试验测得的结果(实测值),与基于实测混凝土自由收缩得到的有限元约束模拟结果(数值模拟)和基于自由收缩预测模型得到的有限元模拟结果(预测模型),建立两组对比,技术路线如图10所示。

图10 约束收缩对比技术路线图Fig.10 Constrained shrinkage comparison technology roadmap
图11为基于28 d龄期内S-1~S-9试验实测值和预测模型绘制的最大误差-最小误差包络曲线,及第S-5组试验和预测模型约束收缩应变曲线。
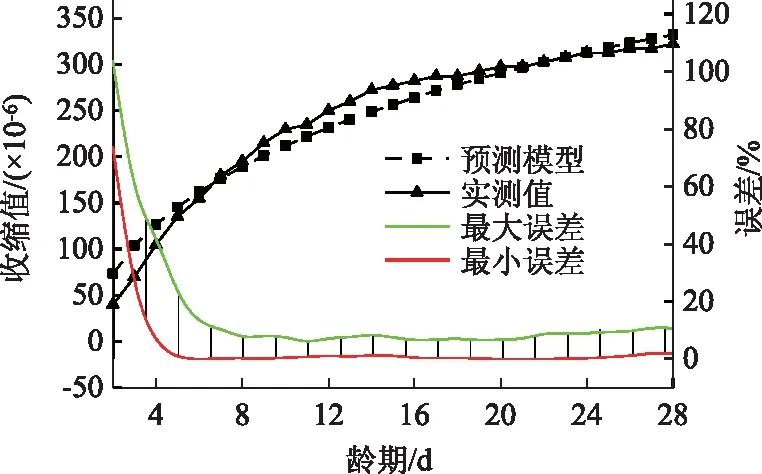
图11 收缩实测值与预测模型结果对比及误差分析Fig.11 Comparison of measured values with prediction model result of shrinkage and error analysis
在混凝土养护初期,混凝土收缩较小,产生较大的误差,随龄期增加误差快速减小,7 d后误差稳定在10%范围内。最大、最小误差差值也呈下降趋势,由于前期收缩值很小,差值最高可达38.40%,7 d后混凝土发展逐渐成熟,差值控制在10%以内。对照S-5组试验实测值和预测模型结果,可以发现两者的约束收缩应变发展趋势相同且有较好的吻合度。自由收缩预测模型能够准确预测混凝土养护7 d后的约束收缩情况,可以指导混凝土约束收缩的设计计算。
为研究上述研究中的误差来源,将本研究所提出的自由收缩模型与混凝土实测的自由收缩量,分别代入约束收缩模型中进行计算,并对计算结果进行分析。
图12为基于28 d龄期内S-1~S-9数值模拟和预测模型绘制的最大误差-最小误差包络曲线及第S-4组数值模拟和预测模型约束收缩应变曲线。
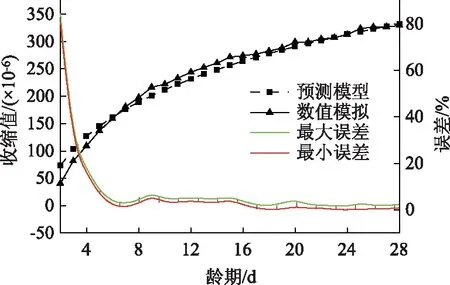
图12 收缩数值模拟结果与预测模型结果对比及误差分析Fig.12 Comparison of numerical simulated result with prediction model result of shrinkage and error analysis
分析可知,误差曲线呈下降趋势,7 d前误差快速减小,7 d后误差稳定在5%范围内。最大、最小误差差值均小于5%。S-4组两条约束收缩应变曲线具有相同的发展趋势且吻合度很高,这验证了收缩预测模型预测自由收缩的准确性。可以看出,本研究提出的预测模型的主要误差来自于两个方面:一个是自由收缩模型的误差,根据本节模型的计算结果可知,此项误差在5%以内;另一个是约束收缩计算模型的误差,包括接触处理、数值误差等方面,占5%以内。总体上看,本研究所提出的早强低收缩玄武岩纤维混凝土自由收缩预测模型以及约束收缩的预测模型可满足实际结构约束收缩的预测。
5 结论
(1)该早强低收缩玄武岩纤维混凝土具有较好的早期基本力学性能以及较小的早期收缩,与普通混凝土相比,其早期收缩至小减小24%,开裂风险较低。
(2)收缩预测模型收缩估算结果对比显示,4种模型均低估了早强低收缩玄武岩纤维混凝土的收缩值。其中CEB-FIP模型与GL2000模型的收缩趋势与实测值基本保持一致,而ACI209模型与王铁梦模型估算结果与实测结果相差较大,不适用于该混凝土的收缩预测。
(3)玄武岩纤维的掺入不会改变混凝土原本的收缩规律,但能有效抑制混凝土的早期收缩,并且掺入量越多,抑制效果越好。基于GL2000模型的早强低收缩玄武岩纤维混凝土收缩预测修正模型能够较好地预测早强低收缩玄武岩纤维混凝土的早期收缩。
(4)修正的GL2000模型基于有限元得到的约束收缩与实测约束收缩和基于实测自由收缩得到的约束收缩数值模拟结果都有良好的拟合度,曲线发展趋势相同且中后期误差较小,预测模型和约束收缩计算模型所带来的误差仅占5%,对预测带栓钉混凝土的约束收缩有指导意义。
