液压夯补强路基动力响应现场试验研究
2022-09-28李天宇崔新壮
李 晋,姜 鹏,李天宇,常 德,崔新壮,
(1. 山东交通学院, 山东 济南 250357;2. 山东大学 土建与水利学院, 山东 济南 250061;3. 济南金曰公路工程有限公司,山东 济南 250101)
0 引言
路基弱碾区或碾压盲区等填筑位置狭窄,小型夯实设备压实功较小且施工效率低下,大型压实机械又不能进场或运行不便,因此这些位置压实效果普遍较差,极易诱发施工质量问题[1-2]。液压夯可以实现高强度、高频率反复施压,且机动灵活施工作业盲区小,用于上述位置可取得良好压实效果[3-5],弥补了路基弱碾区及碾压盲区作业施工质量控制问题的技术空缺,因此采用液压夯进行路基弱碾区及碾压盲区的压实补强施工得到广泛应用。
明确液压夯夯实作用下路基动力响应特征有助于优化液压夯施工工艺、提高路基服役动力稳定性[6],诸多学者们也开展了路基动力响应相关研究。刘本学等[7],冯忠绪等[8]建立了液压夯-土体相互作用力学模型,并通过室内模型试验探究了液压夯用于桥头台背的施工效果;马宗源等[9]借助于离散元数值仿真探讨了影响碎石土地基孔隙率的因素,进而用于评价液压夯动力夯实效果。实际上,在液压夯冲击载荷作用下,介质微元体的惯性不应该被忽略,因为惯性力在动力学中同样能使物体产生变形[10]。研究表明,高应变率、高加载率的动力作用会显著提高被加载介质的屈服强度与瞬时应力。液压夯动力夯实作用下,路基土体应力应变关系与静力下的应力应变关系有很大差异[11-12]。谢永利等[13]探究了液压夯夯实作用在路桥过渡段填料中的动载传递特性,分析了不同路径中动载竖向传递规律。姬猛等[14]通过室内模型试验分析了液压夯实法补强桥台背路基时夯击能随着距夯点距离变化的衰减规律,由此可见原位动力响应测试相比于其他研究手段能够较为真实地反映实际状况。
针对山东省内一般性粉质黏土路基,本研究采用不同量级的液压夯开展现场试验对比研究,分析特定土质下机械-土体相互作用强化机理,探究不同夯击能作用下粉质黏土填料动应力时空响应与加速度响应峰值的变化规律,以期为液压夯相关动力压实研究提供借鉴与参考。
1 动力响应现场试验
1.1 工程概况
本次试验路段选择山东省某改建工程路桥过渡段,施工现场地基分布有可塑、硬塑状态的湿陷性黄土,对试验段现场路基填筑所用的素土及灰土(6%)随机取样后,依据《公路土工试验规程》(JTG 3430—2020)进行土工试验测定并鉴定土质。判定场地内黄土湿陷系数为I级(轻微湿陷),湿陷等级为轻微、中等的一般性粉质黏土,具体土工试验参数如表1所示。试验段路基高度为5 m,采用分层填筑施工,松铺系数为1.3,松铺厚度为26 cm。

表1 土工试验结果Tab.1 Geotechnical test result
为了减少道路占地,右侧设有支挡结构扶壁式挡墙,其厚度为0.5 m,高6.1 m,扶壁厚度0.5 m。挡墙扶壁间隙属于路基弱碾区,拟决定采用液压夯进行压实补强施工。采用某有限公司生产的3种不同型号的高速液压夯实机进行挡墙扶壁间隙处压实补强施工,其具体参数可见表2。

表2 机械技术参数Tab.2 Technical parameters of machinery
1.2 试验方案
现场试验拟采用电阻应变式土压力盒(量程:1.0 MPa,型号:JMYJ-1410,精度:2%F.S)与压电加速度计(量程:100 g,型号:JMCZ-2091,频率:1~1 400 Hz)进行一般性粉质黏土路基动态土压力值与动态加速度监测。采用某技术股份有限公司生产的动态信号测试分析系统及DH5922D采集仪进行动力响应信号的采集与分析。路基分层填筑到规定高度作业面时,采用立方体实心木块放置于压实面上采用压路机压实直至满足规定压实度要求。然后将木块抠出形成立方体坑洞空间,在坑底满铺细砂,水平布设好传感器后再将细砂灌满坑洞,将传感器4壁包围,然后布置好传感器导线继续进行下一层填土压实。整个施工期间注意导线及传感器的防损防潮工作。
现场选取两个挡墙扶壁间隙断面(A断面和B断面),根据传感器布设方案(如图1所示)在路基分层填筑施工期间进行传感器埋设。分层填筑路基顶面施工完毕后,经检测压实度为98%,挡墙扶壁间隙处压实度为96%,含水率为12.0%,可见与正常作业区相比,路基弱碾区压实质量较差。填筑压实完毕后,为防止路基土含水率变化,立即分别采用不同型号液压夯机开展路基弱碾区压实补强:在两个断面规定夯点处采用3.5 t液压夯各进行6次满夯击实,在此基础上在A断面夯点处采用7.0 t液压夯进行6次满夯击实,在B断面夯点处采用5.0 t液压夯进行6次满夯击实,夯实作业的同时数据采集工作同步进行。试验完毕后,切断导线,永久滞留传感器于路基内部。
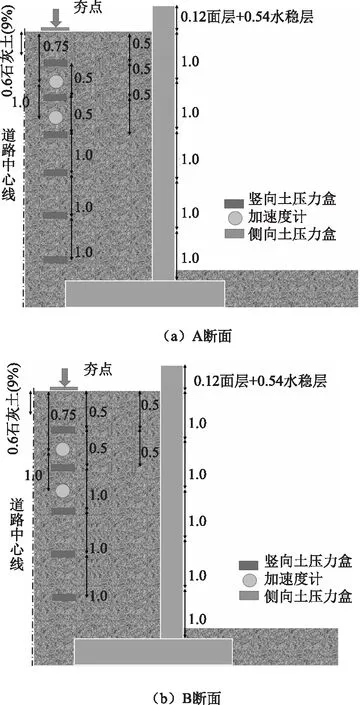
图1 道路横断面传感器布设示意图Fig.1 Schematic diagram of layout of sensors in road cross-section
2 动态响应分析与讨论
2.1 土体动应力空间响应规律
由试验数据可知,随着夯击次数的增加,土体内任意处应力峰值均是先增大后趋于平稳。这是由于土体受到夯实作用,整体刚度逐渐变大后趋于稳定。取夯点竖直方向上不同深度位置处的平均应力峰值,作出应力响应随深度变化如图2所示。

图2 不同夯实作用下应力响应纵向变化曲线Fig.2 Longitudinal variation curves of stress response under different compaction actions
如图2可知,在3.5 t液压夯、5.0 t液压夯与7.0 t液压夯夯实作用下,从夯点以下0.5 m到1.0 m 深度处所测得应力峰值分别损失了62.75%,54.56%和50.59%。3.5 t液压夯在夯点以下1.8 m深度处应力衰减到0.25 MPa以下,而衰减至同样应力值以下,5.0 t液压夯的作用深度可达夯点以下2.4 m,而7.0 t液压夯的作用深度可达夯点以下4.0 m。可见夯击能越大,应力波影响深度越广。同时可以注意到与5.0 t液压夯、7.0 t液压夯夯实效果相比,3.5 t液压夯夯实作用下路基土体不仅应力响应相对较小,且在土壤黏性阻尼和几何阻尼影响下,路基土体应力耗散较快;而在5.0 t液压夯、7.0 t液压夯夯实作用下,由克服土体阻尼而造成的夯击能衰减量相比于3.5 t液压夯的较少[15]。
由试验方案可知,除了竖直方向布设了动态土压力盒,还在路基上部位置,承压面朝向夯点的水平方向上竖直埋设了动态土压力盒以监测动态侧向土压力。由竖直土压力σv可计算得侧向土压力σh,如式(1)所示,不同深度处实测水平向的应力响应如图4~图5所示。
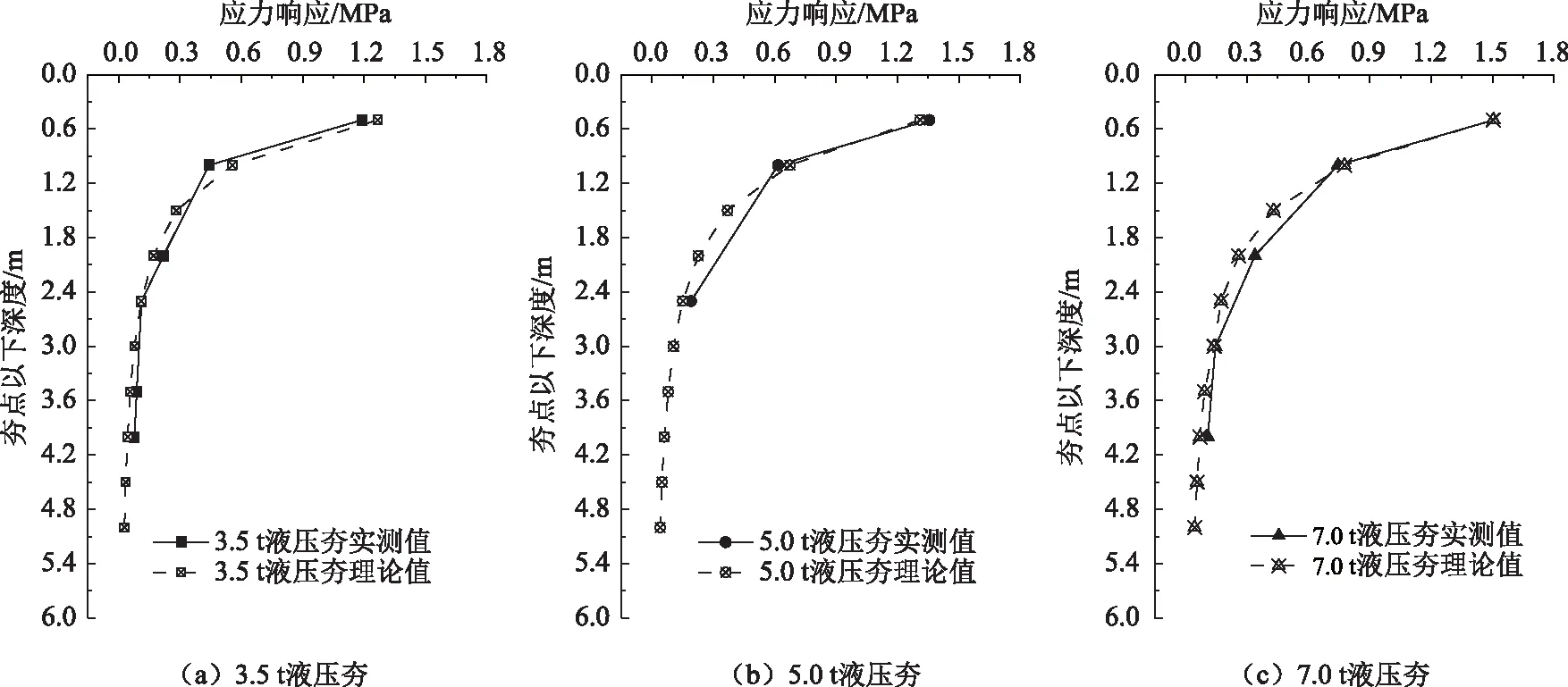
图5 不同夯实作用下的应力响应曲线Fig.5 Stress response curves under different compaction actions
σh=K0σv=λσv/(1-λ),
(1)
式中,K0为侧向土压力系数;λ为土的泊松比。
图3(a)所示的是夯点以下0.5 m深度处水平方向上土体应力情况,应力在0.5 m范围内衰减较慢,超过0.5 m范围外应力迅速衰减。3.5 t液压夯、5.0 t液压夯与7.0 t液压夯夯实作用下,水平向0.5 m 处应力峰值分别损失了18.28%,12.21%和1.93%,水平向1.0 m处,应力峰值分别损失了82.58%,77.37%和72.16%。图3(b)所示的是夯点以下1.0 m深度处水平方向上土体应力情况,3.5 t 液压夯与7.0 t液压夯夯实作用下,水平向0.5 m 处应力分别损失了8.84%,32.39%,在水平向1.0 m处,应力分别损失了23.97%和53.62%。综合图3可知水平方向上,夯击能越大,应力衰减幅度越大。
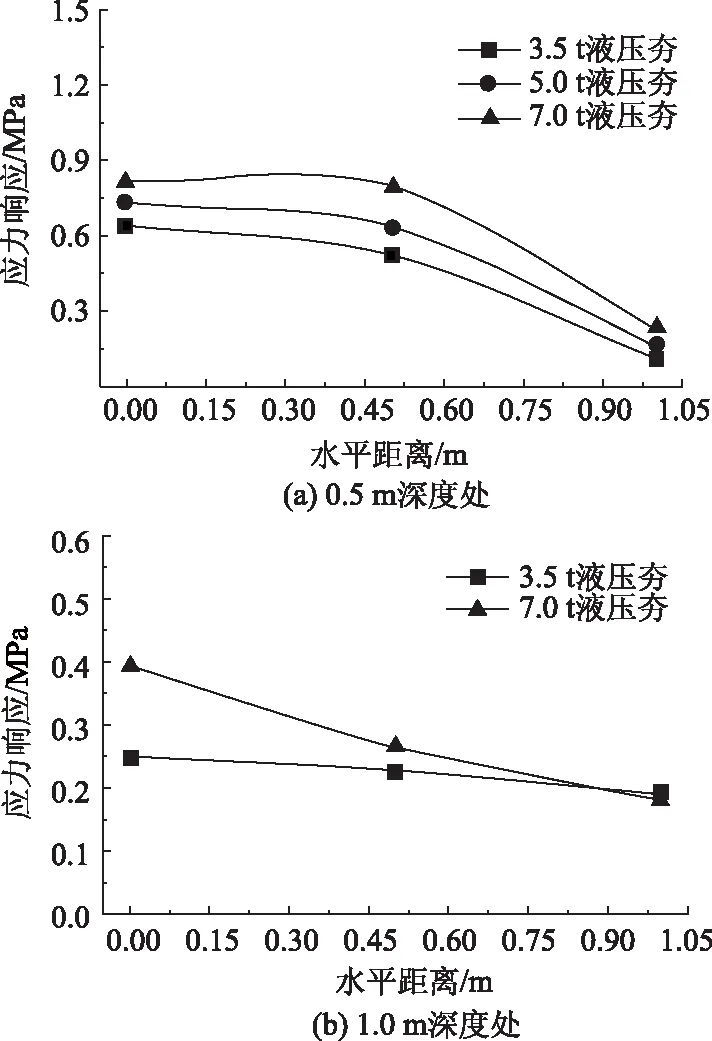
图3 不同深度处应力响应横向变化曲线Fig.3 Lateral variation curves of stress response at different depths
2.2 竖向土体动应力解析
基于热力学领域来看,液压夯动力冲击加载的过程属于绝热过程,夯实作用使路基表层土体产生了一部分塑性变形,即液压系统将夯锤抬高产生的重力势能,在夯锤-土体相关作用中转化成了路基土体的冲击压缩能和塑性变形能[16]。因此学者们多将夯锤-土体相互作用过程看作是动力学中的非完全弹性碰撞[17],但考虑实际工况中不同的参振土体性质与不同的夯锤技术参数,因此,基于本试验工况,拟提出一种作用于一般粉质黏土的液压夯动力补强应力解析模型。
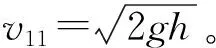
m1v11+m2v21=m1v12+m2v22,
(2)
式中,m1为夯锤质量;m2为参振土体质量。
定义一个恢复系数k=(v22-v12)/(v21-v11),可体现土体-夯锤相互作用过程中的能量消耗。土体-夯锤相互作用过程视为完全非弹性碰撞时k=0;土体-夯锤相互作用过程视为完全弹性碰撞时k=1;而当0 (3) 恢复系数k与参振土体性质有很大关联,假设参振土体均质且为素土,此时由前文土工试验检测可知此时土体含水率为12.0%,为最佳含水率。由现场夯点处所测的压实度为96%可知此时土体密度为2.075 g/cm。本试验中夯击6次后土体已经趋向于密实状态,在此基础上取k=0.80,取锤体行程的1.72倍的圆柱求得体积后计算参振土体的质量m2。土体-夯锤相互作用瞬间完成后,锤体给土体产生一个速度v22,进而实现对土体的夯实。考虑将地基简化成图4所示的阻尼弹簧体系,建立运动方程如式(4)所示。 图4 非完全弹性碰撞半空间夯实模型Fig.4 Incomplete elastic collision half-space compaction model (4) (5) 相应于最大加速度的时tα: (6) 将夯锤底面压力视为均匀分布,则此时应力峰值σdmax为: (7) 不同量级液压夯作用于土体表面产生的应力峰值σdmax通过前文相关机械技术参数与土体参数可计算而得,然后借助于竖直集中荷载作用下的附加应力解析解(Boussinesq解),可计算圆形均布荷载作用下土体内竖直方向上任一点z深度处的附加应力为: (8) 由此可得如图5所示的夯点正下方应力响应理论值变化情况。 通过图5可见不同深度处解析模型所得的计算值与实测值基本一致,表明将机械-土体相互作用视为非完全弹性碰撞的基础上,取恢复系数k为0.8,参振土体为最佳含水率下的一般粉质黏土土质,参振土体体积取底面与锤体底面积一致,高为锤体行程的1.72倍的圆柱体,所得计算值与现场实测值相符程度较高,该参数取值有助于为一般粉质黏土路基液压夯补强应力计算提供参考。 固体静力学中往往忽略物体介质惯性导致的可变形性,单纯基于静力平衡状态计算物体的受力与变形。而介质微元体的惯性在动力学中不应该被忽略,若动力加载时间远远小于被加载介质中应力波传递时间,此时应力波传播与相互作用效应不应该被忽略。作出如图6所示,3.5 t液压夯作用下夯点竖直方向上土体应力时程曲线。 图6 不同深度处应力时程曲线Fig.6 Time history curves of stress at different depths 图6描述了夯点以下不同深度处应力时程曲线。可以看到路基表层土体中应力波呈现出较为剧烈的冲击特征,由于土体本身的惯性使得应力波又出现了一个较小的波峰,随即受到应力波的传播与相互作用效应,土体应力值震荡波动直至消散。而在路基深层土体中,应力波呈现为弹性振动特征,弹性波动一下,动应力立即恢复归0状态。路基表层(0.5 m深度处)在3.5 t液压夯作用下应力波的加载周期为5 ms,而路基深层(4.0 m深度处)的应力波的加载周期为9 ms。 计算3种液压夯夯击作用下应力值波动到恢复归0状态(应力波作用周期)的时长。通过对比时间差均值可知,夯点以下0.5 m深度处,3.5 t,5.0 t 和7.0 t这3种液压夯的应力波作用周期分别为1.466 s,2.223 s和2.902 s。由此可见冲击能越大,应力波作用周期越长。 液压夯夯实作用会使土体介质微元体瞬间产生明显加速度,土体的运动和变形也会受到加速度所引起的惯性力影响,短时间内的动力加载过程中会产生幅值变化较大的动应力集中,进而产生特殊的局部破坏效应[18]。由于路基分层填筑施工过程中损坏了部分加速度计,仅以3.5 t和5.0 t液压夯为例,作出加速度峰值随着土体深度的变化情况如图7所示。 图7 加速度响应随着深度的变化Fig.7 Acceleration response varying with depth 由图7可以看到,在3.5 t液压夯作用下,夯点以下0.75 m深度处加速度峰值为2.238 m/s2,夯点以下1.25 m深度处仅为0.464 m/s2,土体加速度响应衰减了79.27%。而在5.0 t液压夯作用下,夯点以下0.75 m深度处加速度峰值为2.786 m/s2,夯点以下1.25 m深度处为0.899 m/s2,土体加速度响应整体衰减了67.73%。由此可见竖向方向上加速度与应力衰减情况相同,冲击能越大,同一深度处土体加速度响应衰减幅度越小。 进一步地,图8所示为5.0 t液压夯夯实作用下土体加速度响应时程曲线。夯击加载土体产生正向加速度,锤体重力势能转化为土体动能。由加速度时程曲线形态可知,锤体-土体相互作用瞬间,夯点以下0.75 m深处土体振动速度先急速增加对应锤体夯击作用时段,随后速度缓慢增加至最大值对应夯击作用完成之后,此深度处的土体表现出较多的塑性状态,直接产生不可恢复的塑性形变。而由1.25 m 深处加速度值变化情况可知,土体振动速度衰减为0之后又反向加速,说明夯击作用完成之后,相较于0.75 m深处,1.25 m深处土体表现较多的弹性状态,大部分土体形变可恢复。 图8 加速度时程曲线Fig.8 Acceleration time history curves 通过开展本次液压夯夯实粉质黏土动力响应现场试验研究,得到以下结论: (1)夯击能越大,路基土体中应力竖直方向上传播时损耗越小,应力波影响深度越广。夯点正下方0.5 m深度处,水平方向上应力衰减幅度先慢后快,夯点正下方1.0 m深度处的水平方向上,随距离增大衰减幅度增大。总体水平方向上夯击能越大,应力衰减幅度越大。 (2)将机械-土体相互作用视为非完全弹性碰撞的基础上,取恢复系数k为0.8,参振土体为最佳含水率下的一般粉质黏土土质,参振土体质量取底面与锤体底面积一致、高为锤体行程的1.72倍的圆柱体,所得计算值与现场实测值相符程度较高。 (3)路基表层土体惯性会使应力波产生第2个波峰,随后应力值在应力波的传播与相互作用效应下发生震荡直至应力消散归0,而在路基深层土体处,动力夯实作用下表现为弹性振动特征。冲击能越大,同一深度处应力波作用周期越长。 (4)冲击能越大,应力波传递到夯点以下同一深度处土体加速度响应衰减幅度越小。由加速度时程曲线形态可知,夯点以下0.75 m深处土体表现出较多的塑性状态,1.25 m深处土体表现较多的弹性状态。
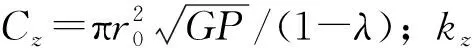
2.3 竖向土体应力时程响应规律
2.4 土体加速度响应规律


3 结论
