高低屋盖表面风荷载特性的数值模拟研究
2022-09-28孙建波
孙建波
(哈尔滨工业大学建筑设计研究院有限公司,哈尔滨 150090)
0 引言
高低屋盖是比较常见的结构形式,由于受高屋盖的干扰导致低屋盖表面以及高低屋盖交接位置风场特性较为复杂,高低屋盖的高度差以及屋盖跨度都是影响低屋面流场特性的主要原因。在此类结构设计过程中要详细考察风压分布特性和风荷载取值,确定极值风压的位置以及周围流场湍流发展全过程,从而确保结构抗风设计的安全性。
在国内外研究中,王云杰、李秋胜等[1,2]通过现场实测获得强热带风暴登陆前后的风速和风压数据,分析了强风环境下的近地风场特性。但实测受场地区位等限制,后续罗颖、Chen、高阳等[3-5]通过建立缩尺模型在风洞中进行试验并设立监测点研究屋盖的风荷载分布情况。随着计算机的发展,相较于风洞试验和现场实测,数值模拟分析成本低,参数变换简便同时具有不错的准确度。刘博雅、KHIN等[6-8]利用CFD数值模拟方法对高低屋盖在风雪流作用下积雪堆砌情况及流场变化进行总结。朱亚洲[9]通过对比分析选择最优的湍流模型,研究了风向角、房屋开洞、山墙等因素对风压分布的影响。夏少军[10]采用二次开发手段导入指数型风剖面的数值模拟方法总结出不同山体布置形式对低矮房屋表面风压分布的规律。
根据朱亚洲对比Standard k-ε、SST、RNG k-ε和Realizable k-ε湍流模型模拟结果,文中选择Realizable k-ε湍流模型在雷诺数为20000的均匀流场中对高低屋盖二维模型进行风荷载数值模拟,分析高低屋盖高度差和屋面跨度等参数影响下平均风压系数的变化规律以及其流场漩涡形成与脱落的位置,从而确定屋面风压最不利分布区域,为实际工程的设计提供理论参考。
1 计算方法与结果验证
1.1 控制方程
文献[11]提出,当时均应变率很大时,Standard k-ε湍流模型会产生负的正应力。为了使流体符合湍流运动的物理定律,必须给正应力施加某种约束。文献[12]表示要实现这种约束,湍动粘度计算式中的系数Cμ应该与应变率相关联,而不能认定为常数。于是,便提出了Realizable k-ε湍流模型。模型中k和ε的输运方程如下:
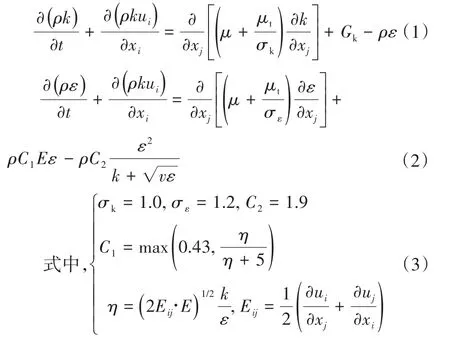
1.2 计算模型与网格
文中验证模型如图1所示,取一平屋盖,屋盖高度h=15,长度D=30,其计算域取一长方形,其在模型前流场、后流场和高度的尺寸分别为5D、15D和8h。计算域的网格采用结构化网格,为了更精确地监测模型表面的参数,对模型边缘区域进行了局部加密,最小网格高度为0.05,对应y+<30。

图1 计算模型、边界条件及计算域整体网格
计算域入口边界采用速度入口,入流采用速度沿高度不变的均匀流,上边界采用对称边界条件(Symmetry),下表面及模型表面采用无滑移壁面(Wall),出口边界采用压力出口。压力速度耦合方法采用SIMPLEC算法,残差收敛值设为1×10-6。
1.3 计算结果分析与讨论
为了验证模拟方法的准确性,首先,提取平屋面平均风压系数模拟结果并与风洞试验结果[13]及三维模拟结果[14]进行对比分析,如图2所示,文中模拟结果在前流场屋檐处大于三维模拟以及风洞试验结果,这是因为二维模型屋面实际为三维模型的一条中线,其直接受入流风场作用,而相比与三维模型所受两侧屋面干扰、分流后的结果来说,其风压要略大。但屋面整体数值与试验结果比较吻合,由此可见,采用二维模拟方法可以有效反映屋面中线风压分布情况,从而说明文中模拟方法及参数设置的合理性。

图2 屋面平均风压系数比较
2 高低屋盖屋面风压分析
通过上述验证后的模拟方法对高低屋盖表面风压分布特性进行研究。下文主要通过改变屋盖高度差H及跨度L分析高低屋盖风压的变化规律,模型参数如图3所示。试验分别进行高度差为0.5H、H、1.5H、2H和屋面跨度为0.5L、L、1.5L、2L共8个工况的数值模拟试验,分别在高、低屋面均分设置9个测点,监测屋面风压的时均变化量。
图3 参数分析模型
2.1 高度差对平均风压系数的影响
图4为不同屋面高度差的屋面平均风压系数分布情况,以测点10为界限,左侧为低屋面,右侧为高屋面。首先,在屋面跨度保持不变的情况下,低屋面在高度差小于H时的风压从左向右呈递减趋势,而随着高度差的增加,低屋面风压由负压向正压转变,屋面整体的风压数值呈现先减小后增大的趋势,并从低屋面左侧向右侧逐渐增大。高屋面的平均风压系数最大值出现在离最左边缘1/4L处,其值为12.3。高屋面平均风压系数皆为负值,且从左向右逐渐减小,随着高度差的增大,高屋面整体平均风压系数越来越大。
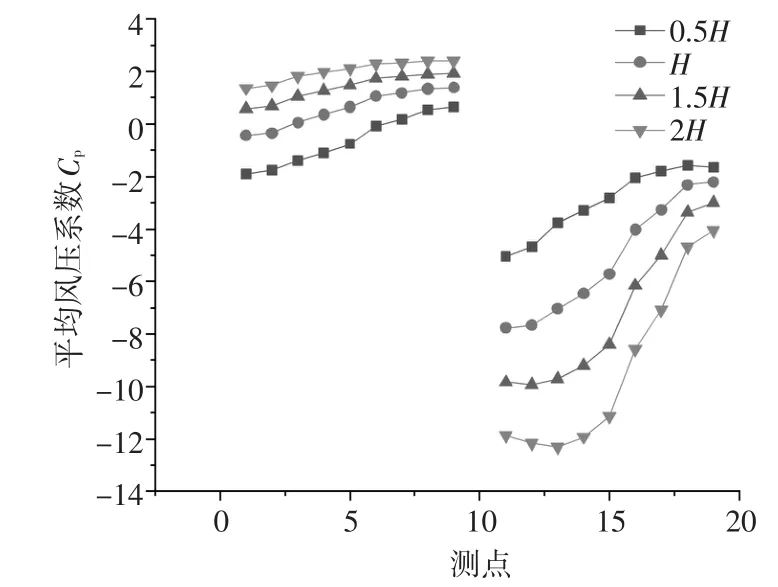
图4 不同高低跨高差下平均风压系数
2.2 屋面跨度对平均风压系数的影响
不同屋面跨度下高低屋面平均分压系数如图5所示,从低跨屋面来看,由于屋面跨度过小,0.5L跨度屋面风压皆为正值,随着跨度增加,低跨屋面迎风端风压转为负压,并在最长跨度2L时又转为正压,这是由于低跨度屋面流场发展有限,受高跨屋面阻碍较强,所以0.5L跨度屋面整体受正压作用,而随着跨度增大在迎风端产生回流漩涡,使得其产生局部负压,但随着跨度的继续增大,固定高低跨高差对低跨流场的阻碍逐渐减小,则回流作用便不至于产生负压,即低跨屋盖受来流风作用加大,导致整体屋盖风压为正值。对于高跨屋盖而言,同样由于屋面跨度过小的原因,0.5L跨度的屋面平均风压系数峰值达到了-10,但随着跨度增大,流场发展充分,屋盖风压则逐渐减小,但屋面跨度与高度差比值到达2:1时,迎风端产生巨大的负压,屋面整体受风吸的影响也变得更大,并在距迎风端0.5L处达到最大值。

图5 不同屋面跨度下平均风压系数
2.3 流场分析
针对上述结果,文中将从流场发展的角度进行分析,图6为不同高低跨高差下流场的速度等值线图,可以发现低跨屋面在0.5h高度差时基本被湍流漩涡所覆盖,而随着高度差的增大,速度逐渐由负值向正值转变,上方的高速漩涡也逐渐消失,这也说明受高跨屋面的阻碍,回流导致风速增加并逐渐转为正值。结合图7流线图来看,高跨屋面的漩涡很小,随着高度差的增加,其漩涡尺寸慢慢增大并向背风端转移,后流场漩涡也是从下方逐渐向屋面背风端转移。图8和图9分别为不同屋面跨度下的速度等值线图和流线图,对比后可知/0.5L跨度的高低屋面风速皆是负值,但只有低跨屋面产生了漩涡,高跨屋面漩涡还未从后流场漩涡中分离,当屋面跨度增大到L时,高跨屋面漩涡产生,低跨屋面漩涡增大,随着屋面跨度继续增大,两屋面漩涡皆向左侧迎风端转移,这也验证了上述平均风压系数在迎风端达到最大值的结论。
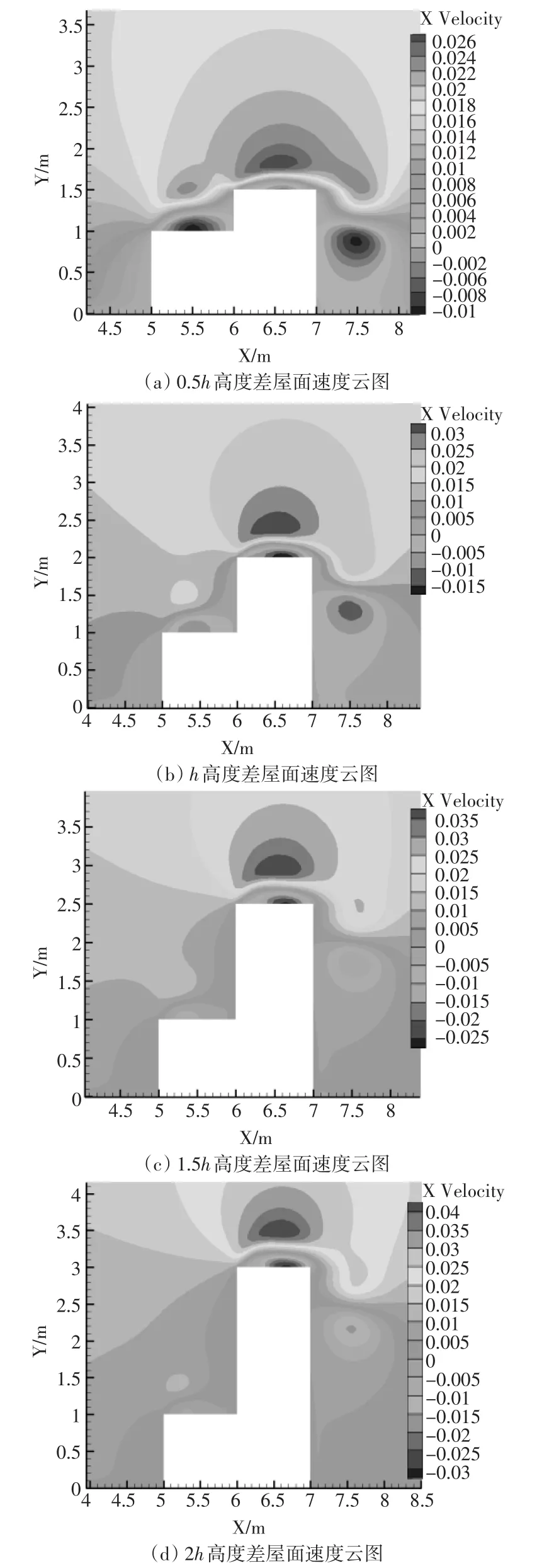
图6 不同高度差屋面速度云图

图7 不同高度差屋面流线图

图8 不同跨度屋面速度云图

图9 不同跨度屋面流线图
3 结语
(1)当屋面跨度不变时,随着高度差的增大,低屋面的平均风压系数呈现先减小后增大的趋势,高屋面的平均风压系数则越来越大,且最大值出现在高屋面上离迎风端1/4L处,其值为-12.3。
(2)当屋面跨度变化时,随着跨度的增加,低屋面平均风压系数变化不大,而高屋面平均风压系数呈先减小后增大的趋势,且当跨度与高度差比值达到2:1时,高屋面的迎风端的平均风压系数达到最大值-12.1。
(3)低跨屋面在0.5h高度差时基本被湍流漩涡所覆盖,而随着高度差的增大,屋面风速逐渐由负值向正值转变。高跨屋面的漩涡较小,随着高度差的增加,其漩涡尺寸逐渐增大并向背风端转移,后流场漩涡也是从下方逐渐向屋面背风端转移。
(4)0.5L跨度的高低屋面的风速皆是负值,流场旋涡仅出现在低屋面,当屋面跨度增大到L时,高跨屋面漩涡产生,高低屋面旋涡随跨度增大而增大,并逐渐向迎风端转移。
