新型钢板组合剪力墙力学性能研究
2022-09-28张国发沈勇周观根杨海平吴旖文
张国发, 沈勇, 周观根, 杨海平, 吴旖文
(1.浙江同济科技职业学院建筑工程学院,杭州 311200;2.浙江大学建筑工程学院,杭州 310058;3.浙江东南网架集团有限公司,杭州 311200;4.浙江潮远建设有限公司,杭州 311200)
0 引言
钢结构作为现代绿色建筑,具有良好的机械加工性能,易拼装,轻质高强,最适合建筑的模块化、标准化、工厂化、装配化和现代化,而混凝土材料作为传统的建筑材料,有很好的抗压性能。由钢结构和混凝土材料组合而成的钢板组合剪力墙能很好的满足小高层、高层住宅项目的需求。
目前国内外学者对钢板组合剪力墙进行一定的研究,Sohel等[1,2]提出了带有J型抗剪连接件的双钢板-混凝土组合结构并通过汽车撞击试验和数值模拟证明了含有连接件的墙体具有良好的整体性能以及优越的抗冲击性能;彭晓彤、顾强等[3-6]对半刚性连接钢框架(强、弱轴)-内填钢筋混凝土剪力墙结构开展一系列试验和理论研究;吴函恒[7]提出了一种新型钢框架-预制混凝土抗侧力墙装配式结构体系(SPW体系),对该体系的受力性能与计算理论进行专题研究;曹晨[8]对钢框架-预制RC剪力墙抗侧力体系进行了理论分析及试验研究;陈敖宜等[9]对国内主要的高层装配式住宅受力体系进行了总结,包括远大可建钢结构公司的钢框架-支撑结构体系、杭萧钢构开发的“钢框架-支撑结构体系”和“钢管束组合结构体系”。但目前新型钢板组合剪力墙的开发研究仍相对较少,不能满足建筑行业对钢板组合剪力墙多样化的需求[10-12]。
因此,文中根据钢板组合剪力墙的构成原则,考虑适应建筑布置的灵活性、制作工厂化、模数化、标准化、装配化等需求,提出新的钢板组合剪力墙形式,为实际工程提供更丰富的选择;对新的钢板组合剪力墙建立相应有限元模型并进行分析计算,验证新型钢板组合剪力墙可行性及规程相应计算公式的适用性,为实际工程提供可行性参考。
1 新型钢板组合剪力墙
新型钢板组合剪力墙由外侧双钢板与矩形钢管、内部空间钢筋桁架焊接而成的具有多个竖向连通腔体的结构单元,如图1所示。新型钢板组合剪力墙内部浇筑混凝土,形成一种以一字型、L型、T型、Z字型为主要构造形式的组合构件。
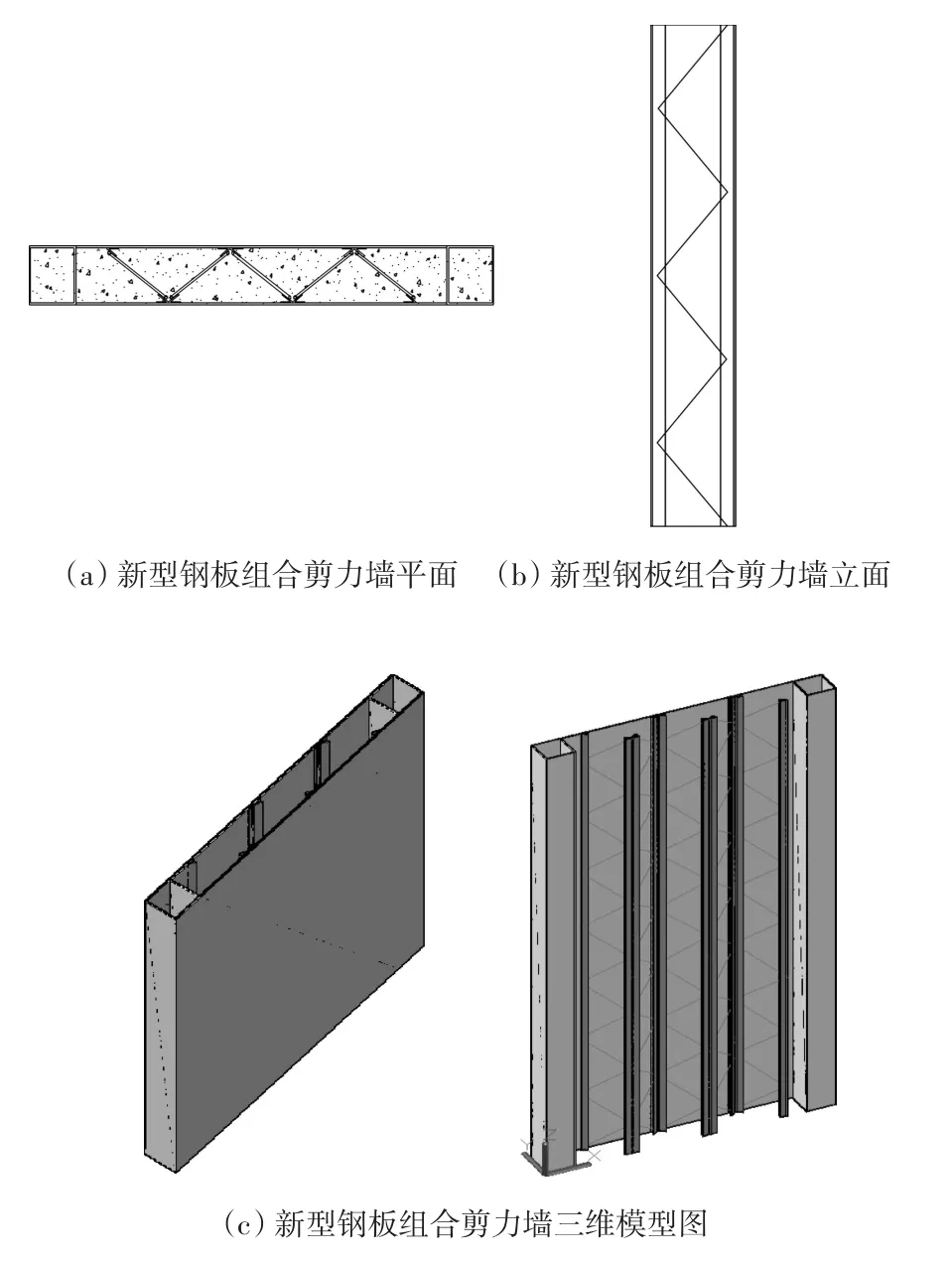
图1 新型钢板组合剪力墙
2 有限元模型
2.1 试件设计
共设计11个新型钢板组合剪力墙模型,试件尺寸如表1所示。

表1 钢板组合剪力墙试件尺寸mm
其中试件一(SCW-1)为基准构件,截面类型为一字型,剪力墙宽1500mm,墙高3000mm,墙厚150mm。剪力墙两端有端柱,端柱尺寸为150mm×150mm,钢板强度等级为Q345,钢板厚度均为4mm,钢筋桁架水平间距及竖向间距均为200mm,钢筋强度等级为HRB400,直径为8mm,钢板组合剪力墙内部空腔灌注混凝土,混凝土强度等级为C35。试件如图2所示。
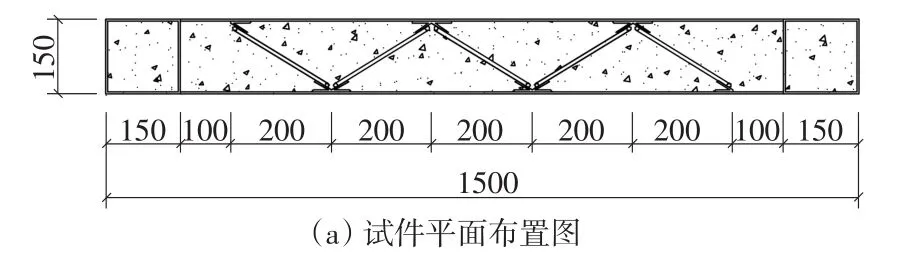

图2 试件布置(单位:mm)
2.2 试件模型
采用有限元软件Abaqus建立新型钢板组合剪力墙有限元分析模型,其中钢板墙体和端柱、角钢、混凝土墙体以及混凝土端柱均采用三维实体单元C3D8R模拟,钢筋桁架采用三维桁架单元T3D2模拟,混凝土组件和钢组件之间的作用设置接触单元模拟。
2.3 参数设置
模型混凝土应力-应变本构关系输入参数见表2。Abaqus中混凝土有5个材料参数,分别为膨胀角、偏心率、双轴与单轴初始屈服强度比σb0/σc0、拉压子午面第二应力不变量的比值K和粘性参数。参考Abaqus软件材料定义中默认的取值,结合文中的多次分析比较,综合考虑收敛性及分析精确性和计算效率,这5个参数的取值见表3。
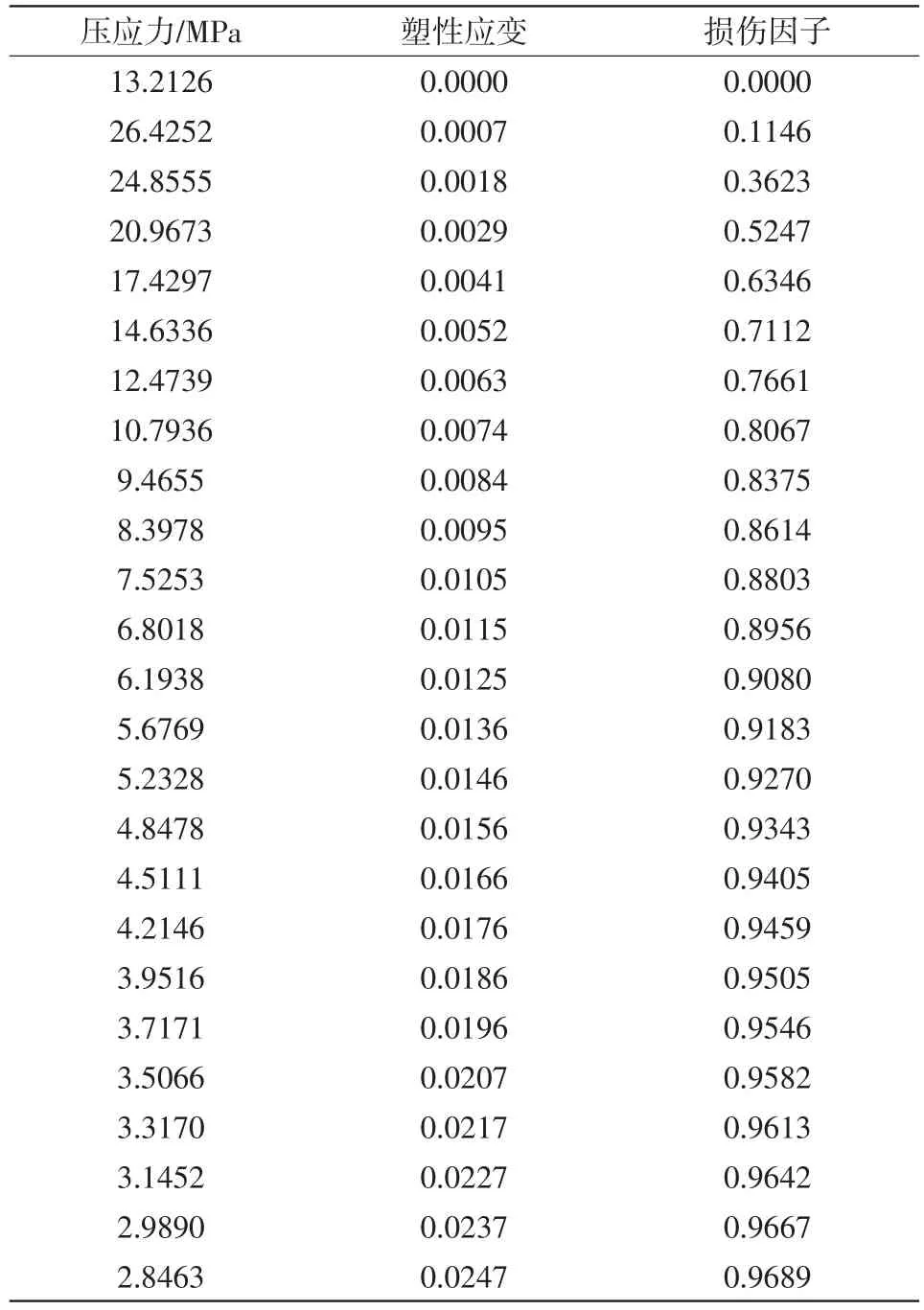
表2 混凝土单轴受压应力-应变本构关系参数

表3 混凝土损伤塑性模型参数取值情况
2.4 非线性类型与接触
文中研究的问题包括几何非线性、材料非线性。塑性理论是解决材料非线性问题的方法,几何非线性问题通常采用增量分析方法。
在用Abaqus建模时考虑到内部混凝土和外部钢板更好的接触,钢板与混凝土接触面法向采用“硬”接触设置,切向采用库伦摩擦模型设置,摩擦系数按照钢板与混凝土之间的常用参数取为0.5。
2.5 各部件间连接关系
建模时角钢与钢板间有共同节点,可实现角钢与钢板的共节点变形;钢筋桁架与角钢间有共同节点,可实现钢筋桁架与角钢间的共节点变形;为简化计算,通过内置操作,实现钢筋桁架与混凝土间的共节点协调变形。
2.6 网格划分
端柱内及钢板墙体内混凝土沿高度方向分为30层,网格尺寸100mm,沿截面边长方向分为3层,网格尺寸50mm。端柱及钢板墙体的钢板沿高度方向网格尺寸为80mm,沿厚度方向分为2层。
3 竖向加载数值模拟
剪力墙在实际工程中被设计为同时承受竖向荷载和水平荷载。竖向荷载作用下可能出现的整体失稳和局部失稳,有可能会显著降低其结构性能,故需要对轴压作用下的钢板组合剪力墙的力学性能进行研究。采用Abaqus对构件进行竖向加载数值模拟。
3.1 荷载及边界条件
对试件SCW-1墙体底部施加轴x、y、z三向位移约束及绕x、绕y、绕z轴转角约束,实现墙体底部固定约束;对墙体顶部施加轴x、y向位移约束及绕x、绕z轴转角约束,释放竖向变形及绕y轴转动。在加载顶端设置参考点,设置试件顶面与参考点之间的变形耦合约束,通过对参考点施加竖向位移(20mm)模拟轴压工况。
3.2 破坏形式
以基准构件SCW-1为例,介绍钢板组合剪力墙在竖向加载下的破坏形式。加载初期,墙体应力随着荷载的增加而均匀增加,墙体中部首先进入屈服阶段,随着荷载的进一步增加,墙体在平面内向一侧发生较大变形而破坏。墙体发生破坏时,组合墙体的钢板、角钢和钢筋桁架、混凝土各部分应力分布以及混凝土与钢板间的接触应力分布如图3所示。

图3 试件应力分布图
加载过程中,荷载与组合墙体竖向变形关系曲线如图4所示;荷载与组合墙体平面外变形关系曲线如图5所示;荷载与组合墙体平面内变形关系曲线如图6所示。从图6中可以发现,随着荷载的增加,组合墙体先是向平面内一个方向发生变形,当荷载达到墙体极限承载力后,墙体在平面内向相反方向发生较大变形而破坏。
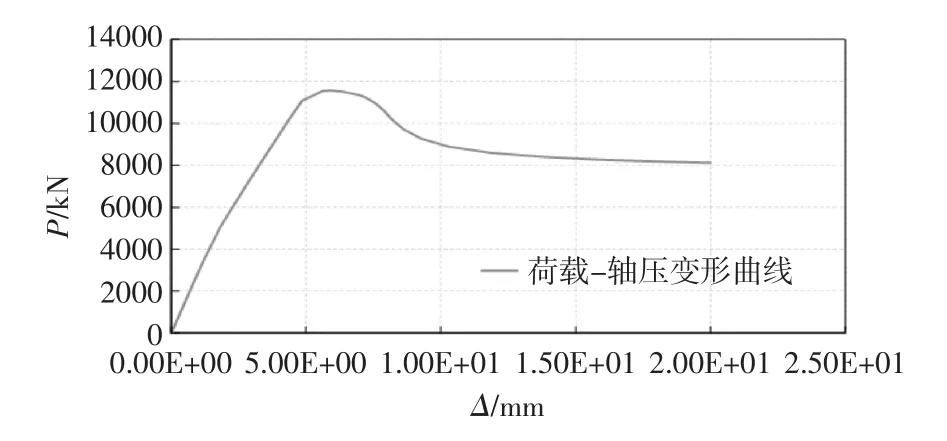
图4 荷载与组合墙体竖向变形曲线
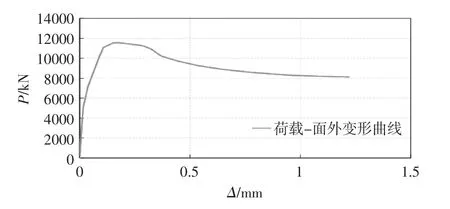
图5 荷载与组合墙体平面外变形曲线
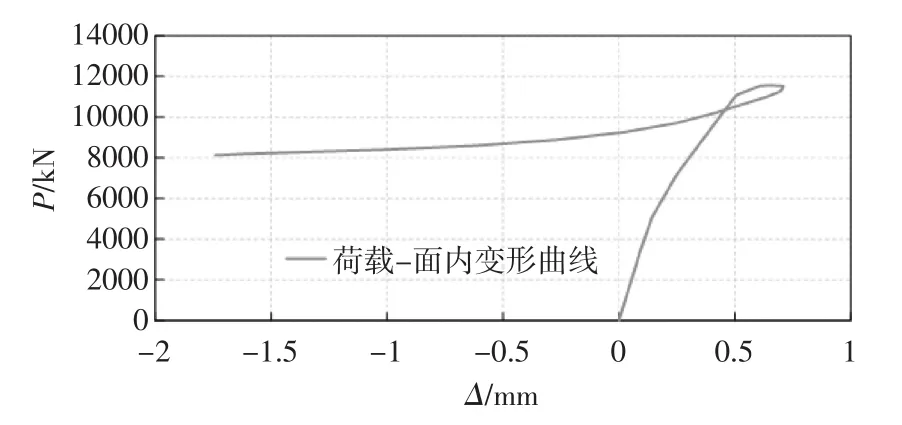
图6 荷载与组合墙体平面内变形曲线
3.3 参数化分析
对SCW-1~SCW-11等11个试件进行竖向加载数值模拟,其极限承载力统计如表4所示。
比较试件SCW-1~SCW-3可以发现,高宽比是影响组合墙体受力的一个重要因素,墙高保持3000mm不变,当墙宽从1200mm减小到600mm时,墙体的极限承载力从11565kN降低到8576kN。比较试件SCW-1、SCW-4~SCW-7可以发现,钢筋桁架竖向间距或水平间距从200增加到400mm时,墙体的极限承载力几乎没有变化,分析认为,钢筋桁架刚度与组合墙的钢板、混凝土部分刚度相比较小,对组合墙体的承载力几乎没有影响,钢筋桁架布置属于组合墙的构造部分。比较试件SCW-1、SCW-8、SCW-9可以发现,组合墙体的钢板厚度从4mm增加到6、8mm时,组合墙的极限承载力从11565kN分别增加到13827kN和16053kN,由此可见,增加钢板厚度可以大幅提高组合墙体的承载力,但考虑到建造成本需要控制用钢量,4mm厚钢板已能满足结构受力要求。比较试件SCW-1、SCW-10、SCW-11可以发现,组合墙体的厚度从150mm增加到180、200mm时,组合墙的极限承载力从11565kN分别增加到12961kN和13855kN,由此可见,增加墙体厚度可明显提高组合墙的承载力,但考虑到建筑功能及构造要求,墙体厚度不宜过大,一般墙厚取为150~200mm较为合适。
4 拟静力推覆分析
剪力墙作为高层、超高层建筑的主要抗侧力构件,其抗震性能和抗震设计方法的研究对保证结构安全,减小地震灾害具有重要意义。剪力墙的抗震性能一般从强度、刚度、延性、耗能能力、刚度退化等方面来衡量,剪力墙的抗震设计则包括承载力计算方法、延性控制、构造措施等方面。通过有限元拟静力推覆模拟分析研究组合剪力墙地震作用下的受力性能。
4.1 荷载及边界条件
对标准试件SCW-1墙体底部施加轴x、y、z三向位移约束及绕x、绕y、绕z轴转角约束,实现墙体底部固定约束;对墙体顶部施加轴y向位移约束及绕x、绕z轴转角约束,释放竖向变形及绕y轴转动。在加载顶端设置参考点,设置试件顶面与参考点之间的变形耦合约束,对参考点施加竖向荷载,荷载按墙体轴压比0.4取值,通过对参考点施加水平位移(50mm)模拟水平拟静力推覆工况。
4.2 破坏形式
对试件SCW-1进行水平位移加载时,组合剪力墙左侧底部为受拉区,右侧底部为受拉区。随着荷载的增加,钢板受拉区和受压区分别达到屈服强度而进入塑性,如图7(a)所示;角钢及钢筋桁架应力变化与钢板相同,如图7(b)所示;混凝土墙体受拉区和受压区也分别达到屈服强度而进入塑性阶段,如图7(c)、图(d)所示,从图中可以看出,仅在组合墙体受拉区和受压区处存在混凝土与钢板间的接触应力。

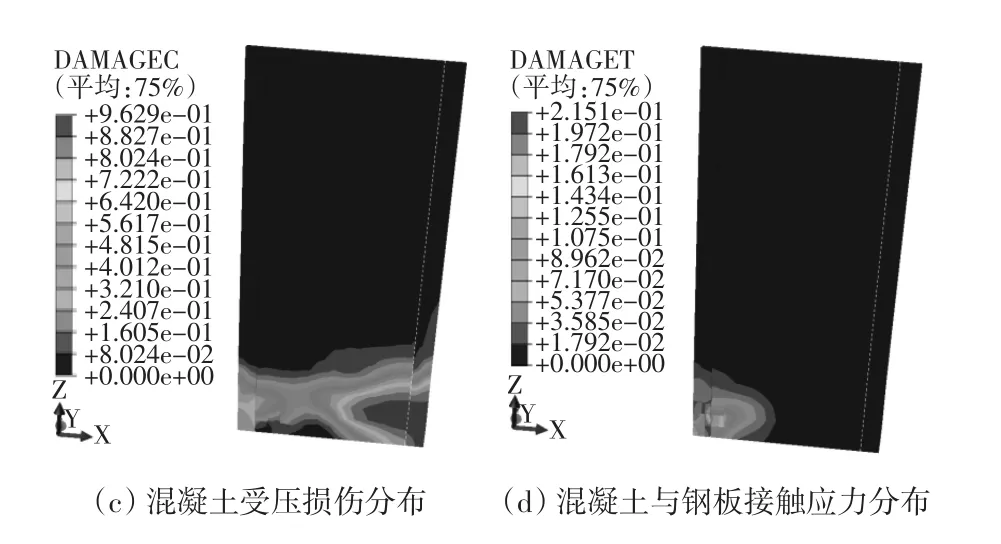
图7 试件应力分布图
加载过程中,荷载与组合墙体水平变形关系曲线如图8所示。从图8中可以发现,随着荷载的增加,组合墙体荷载与水平位移近似呈线性增加,此时墙体各部分处于弹性受力阶段;当荷载达到墙体极限承载力后,组合墙体进入塑性阶段,水平位移快速增加而最终破坏。
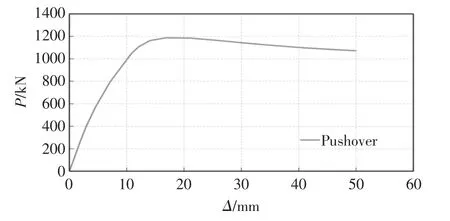
图8 荷载与组合墙体水平变形关系曲线
5 水平循环加载模拟分析
5.1 荷载及边界条件
对标准试件SCW-1墙体底部施加轴x、y、z三向位移约束及绕x、绕y、绕z轴转角约束,实现墙体底部固定约束;对墙体顶部施加轴y向位移约束及绕x、绕z轴转角约束,释放竖向变形及绕y轴转动。在加载顶端设置参考点,设置试件顶面与参考点之间的变形耦合约束,对参考点施加竖向荷载,荷载按墙体轴压比0.4取值,通过对参考点施加水平位移模拟水平往复加载,加载制度如图9所示,共28个荷载步,先正向加载,再反向加载,位移幅值最大值为50mm,每次循环增幅为5mm。
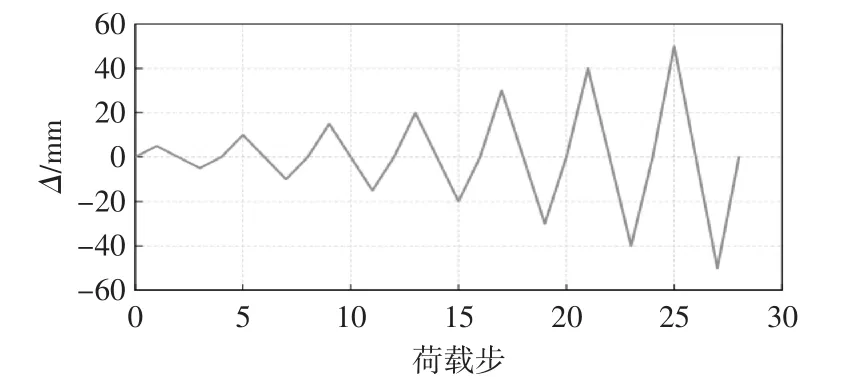
图9 水平荷载加载制度
5.2 破坏形式
标准试件SCW-1在水平往复加载下受力至破坏的发展过程可分为3个阶段:
(1)弹性阶段。此阶段试件未发生明显的鼓曲和钢板撕裂,混凝土未发生明显的压碎现象,钢板和混凝土之间的粘结未发生破坏,试件的顶点水平位移荷载曲线基本呈线性发展。
(2)塑性强化阶段。随着荷载的增加,在试件的两侧开始出现鼓曲和钢板撕裂现象,钢板和混凝土之间的粘结也逐渐破坏,随着水平位移的增大,鼓曲从墙体两侧逐渐向中部发展,钢板撕裂也逐渐扩展,混凝土逐渐被压碎,试件刚度不断降低,直至水平荷载达到峰值。
(3)破坏退化阶段。水平荷载达到峰值后,钢板屈服和混凝土压碎的范围基本达到极限,承载力开始下降,混凝土逐渐退出工作,持续增大的水平位移使得钢板撕裂迅速开展,直至贯通。
试件SCW-1水平荷载-位移骨架曲线如图10所示,试件SCW-1破坏时各部分受力情况如图11所示。

图10 荷载-位移骨架曲线
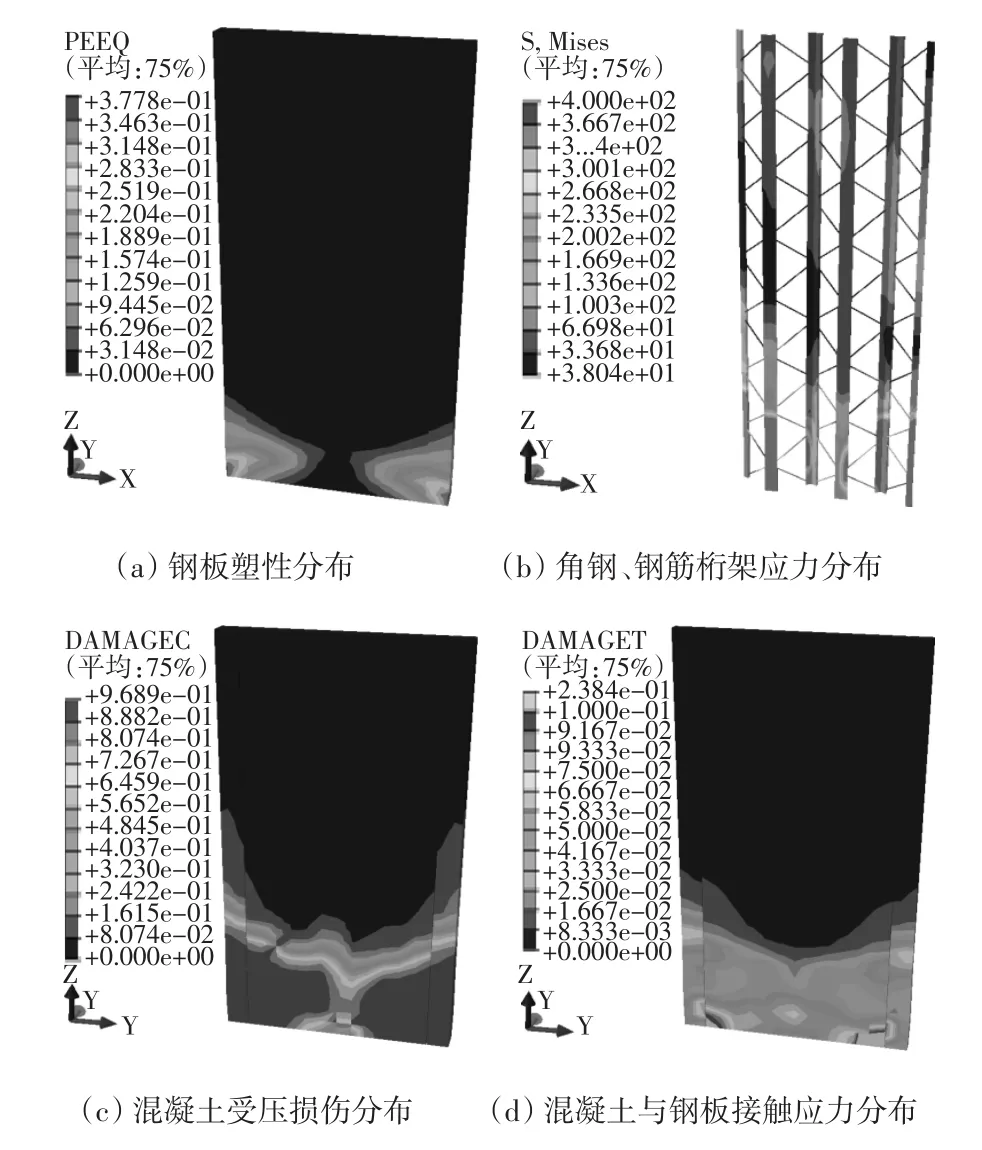
图11 试件应力分布
5.3 滞回曲线
试件SCW-1顶点水平荷载-位移(p-Δ)滞回曲线如图12所示。由图12可知,当加载位移较小时,滞回环面积相对较小,荷载和位移大致呈线性关系;当荷载达到峰值承载力后,每一圈滞回曲线的承载力开始下降。数值模拟滞回曲线比较饱满,没有出现明显的捏拢效果,分析原因是建模时把钢筋骨架整体嵌入至整个模型中,未考虑钢筋与混凝土之间的粘结滑移。
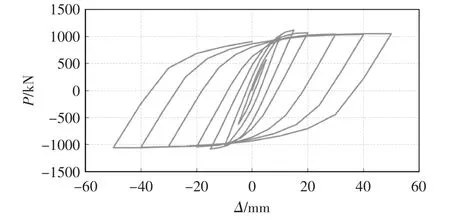
图12 荷载-位移滞回曲线
6 墙体轴压承载力设计方法
表5列出有限元计算承载力和规范公式计算轴压承载力的对比关系,其中材料强度取值分别为钢材屈服强度和混凝土轴心抗压强度标准值。有限元计算构件轴压极限承载力和规范公式计算的构件轴压极限承载力较为接近,验证了规范公式计算新型钢板组合剪力墙轴压极限承载力的适用性。

表5 构件轴压极限承载力 kN
7 墙体压弯承载力计算公式验证
按抗弯承载力计算公式计算部分试件的极限荷载,并考虑效应,材料强度取值分别为钢材屈服强度和混凝土轴心强度标准值,计算值与试验结果对比如表6所示。有限元计算构件抗弯承载力和规范公式计算的构件压弯承载力较为接近,验证了规范公式计算新型钢板组合剪力墙压弯承载力的适用性。
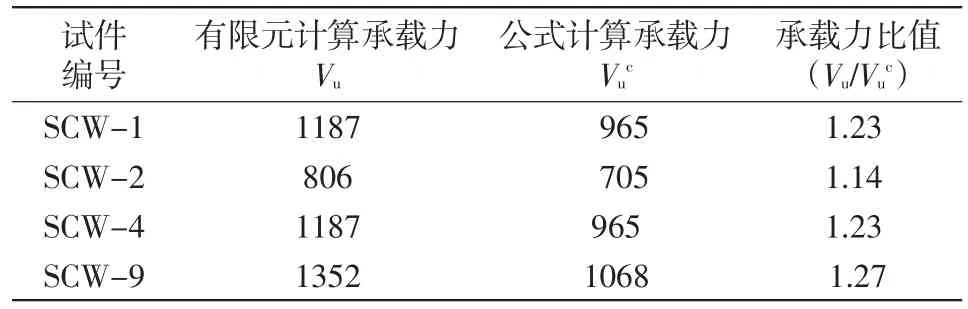
表6 抗弯承载力对比kN
8 结语
(1)钢板组合剪力墙在竖向加载、水平拟静力推覆及水平循环加载下均表现出较好的承载能力,受力及变形趋势与现有常用钢板剪力墙相一致,符合理论预期。
(2)通过参数化分析发现,随着高宽比的增大,墙体的竖向极限承载力有较大幅度的降低;钢筋桁架竖向间距或水平间距变化,墙体的竖向极限承载力几乎没有变化,钢筋桁架布置属于组合墙的构造部分;增加钢板厚度可以大幅提高组合墙体的竖向承载力,但考虑到建造成本需要控制用钢量,4mm厚钢板已能满足结构受力要求;增加墙体厚度可明显提高组合墙的竖向承载力,但考虑到建筑功能及构造要求,墙体厚度不宜过大,一般墙厚取为150~200mm较为合适。
(3)通过有限元计算承载力与规范公式计算承载力比较,验证了轴压承载力、压弯承载力作用下规范公式的适用性,通过规范公式计算的承载力可以为新型钢板剪力墙应用于实际工程提供参考。
