基于改进人工势场法的自动驾驶路径规划方法
2022-09-28马庆禄黄光浩
马庆禄,黄光浩
(重庆交通大学交通运输学院,重庆400074)
1 引言
近年来,自动驾驶技术的成熟使得无人车逐渐走入大众的视野。想要保证其安全平稳的运行,精确的路径规划是必要的。移动机器人的路径规划是其重要的分支之一,而自动驾驶车辆是移动机器人的一种实体形式,因此许多学者将移动机器人路径规划的方法应用于自动驾驶车辆的规划之中。
应用较多的算法主要有基于搜索的方法:A*算法[1]、基于采样的方法:PRM概率图算法和RRT快速搜索随机树[2-3]、基于离散优化的方法:贝塞尔曲线和三次样条插值曲线[4-5]、还有人工势场法[6]、智能优化算法如遗传算法[7]等。其中人工势场法是路径规划研究中比较成熟和实时性较好的规划方法,其原理简单、计算量不大、对于未知环境的应对能力较好,规划中实时考虑周围障碍物的情况且便于控制。但也存在目标不可达问题和容易陷入局部极小值的情况,这会导致复杂环境下路径规划失败。
针对人工势场法可能存在的问题,众多学者对其进行了改进。Sato提出利用拉普拉斯方程求解势能,改进的势场方程有效地消除了极小值点[8]。韩永等在原有的基于相对位置的势场函数基础上,通过构造相对速度引力势场和相对速度斥力势场使机器人能适应未知动态的环境[9]。Saeid Fazli等人采用“沿墙走”方法来解决障碍物附近目标不可达问题以及复杂环境下路径规划问题[10]。李东方等通过调整引力增益系数、斥力增益系数、障碍物的影响范围以及机器人的运动频率等参数以获得最优路径[11]。任彦等提出当机器人陷入局部极小值时对机器人施加附加虚拟控制力以跳出局部极小点[12]。石为人等提出通过建立基于声呐传感器的机器人模型,分别计算不同方向所受的斥力大小,当机器人遇到极小值点时将该区域障碍物连接为整体快速远离该区域[13]。罗乾又等提出设置虚拟目标点的方法,对机器人所受合力为0时通过实际目标点与虚拟目标点的共同作用下摆脱局部极小值[14]。修彩靖等在考虑道路边界的引力约束以及车辆约束后,利用高斯组合隶属函数来优化引力函数,证明势场法适用于在结构化环境下运行的无人车[15]。程志等通过引入机器人实时前进向量来跳出局部极小值点,引入虚拟目标点以逃离障碍物陷阱[16]。温素芳等对于目标点周围存在障碍物提出缩小其影响范围来减小斥力抵达目标点,将障碍物的影响范围分层讨论以逃离局部极小值点[17]。翟红生等利用量子粒子群算法优化势场函数中的增益系数,有效解决了复杂动态环境下随机障碍物的避障问题[18]。梁献霞等通过扇区划分的方法构造虚拟障碍物,使得局部极小值点的机器人在虚拟障碍物和目标点以及真实障碍物三者力的作用下摆脱该区域[19]。魏立新等通过将模糊控制算法和改进的人工势场法结合,解决了U型陷阱和动态障碍物问题[20]。罗强等提出了做机器人对于障碍物势场范围的切线来确定虚拟的逃逸力,通过搜索法来判断障碍物之间的可行区域来逃离极小值点[21]。王洪斌等将改进的二次A*搜索算法与人工势场法相结合,实现了机器人动态规划路径的长度与平稳度较优[22]。
本文介绍了传统人工势场法原理,分析在传统人工势场法进行路径规划时出现目标不可达和局部极小点情况的问题。在改进的引力势场函数上通过设定距离阈值来避免引力过大的导致不能避障问题,在改进的斥力势场函数上,通过引入斥力调节因子并将车辆与障碍物的距离分段讨论,使得自动驾驶车辆能够顺利逃离局部极小点抵达目标。
2 传统人工势场法原理
Khatib[6]于1986年提出人工势场法,基本原理是将自动驾驶车辆运行区域设置为由一个引力势场和若干个斥力势场组成的虚拟的力场环境。预抵达的目标点周围的引力势场对车辆产生吸引力从而“拉动”车辆驶向目标点,吸引力的大小与车辆至目标点的距离成正比,即距离越远吸引力越大距离越近吸引力逐渐减小。行驶过程中遇到的人、其车辆等障碍物会对车辆产生排斥力从而“推动”车辆远离障碍物达到避障的效果,排斥力的大小与车辆至障碍物的距离成反比,即距离越远排斥力越小距离越近排斥力逐渐增大。自动驾驶车辆在目标点与障碍物所产生引力场与斥力场的合力场下能够有效地避开障碍物抵达目标位置。自动驾驶车辆行驶过程中的受力示意图如图1所示。
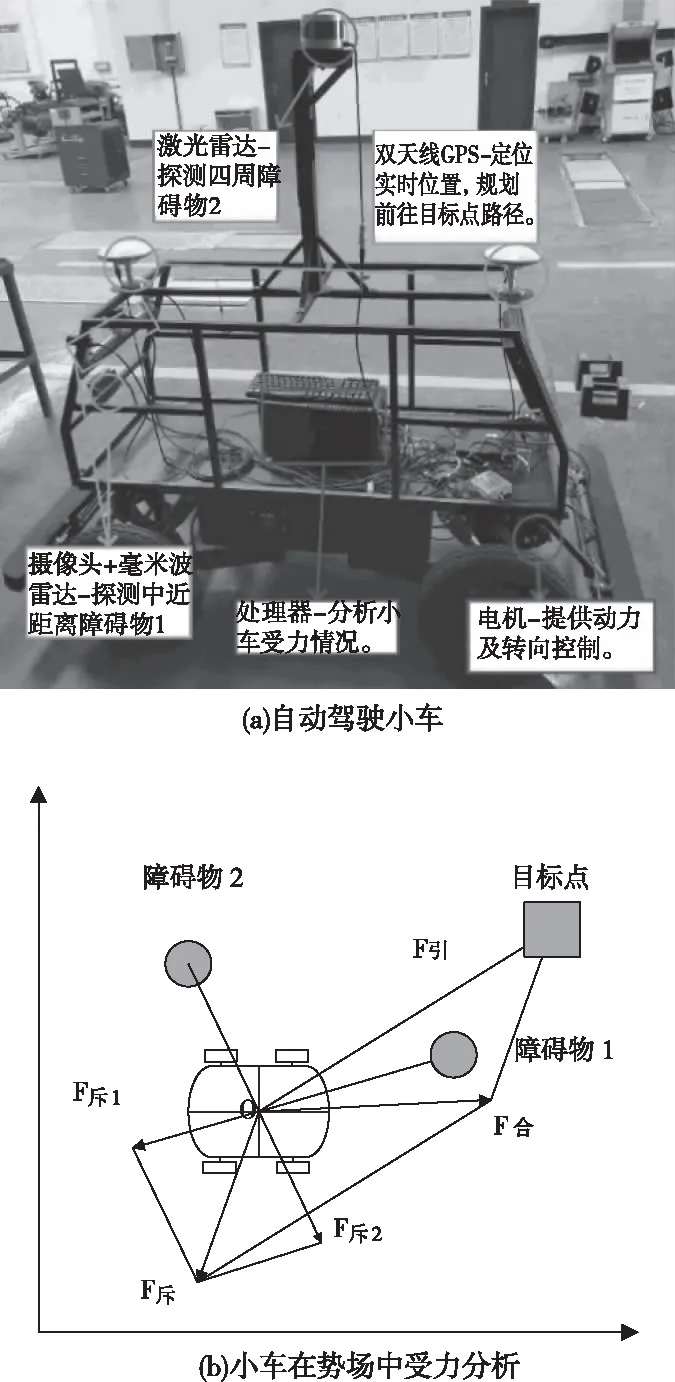
图1 自动驾驶车辆在势场中的受力示意图
2.1 引力场与斥力场函数

(1)
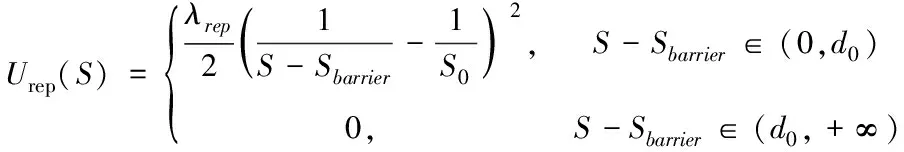
(2)
式中,S为自动驾驶车辆现在的位置(x,y),Starget为预设目标点的位置(xt,yt),λatt为引力势场的常数。λrep为斥力势场常数,Sbarrier为区域内障碍物位置(xb,yb),障碍物对自动驾驶车辆影响的最大距离为d0。对引力势场函数和斥力势场函数分别求解负梯度,即引力与斥力对距离求导可得引力场函数和斥力场函数公式见式(3)和(4)
Fatt(S)=-∇Uatt(S)=-λatt|S-Starg et|
(3)
Frep(S)
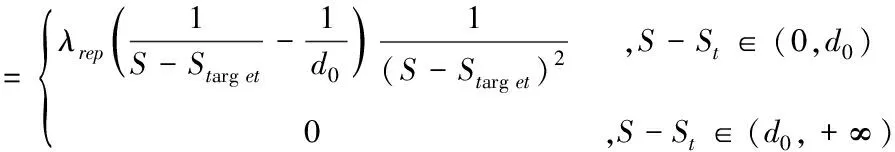
(4)
2.2 合力场函数
自动驾驶车辆在接近目标点的过程中,目标点只有一个但障碍物不止一个,若存在n个障碍物则车辆会受到n个斥力势场叠加起来的作用。可见引力只有单个目标点产生,斥力则会由n个障碍物产生。整个行驶区域内的总势能为引力势能与斥力势能之和,车辆受到的合力为所受的引力和斥力之和,根据上述公式可求得总势能函数与车辆所受合力为
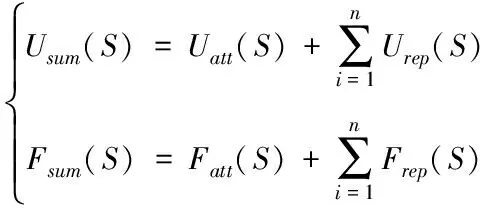
(5)
2.3 人工势场法存在的问题
1)目标不可达问题。当距目标点很近的范围内存在障碍物时,此时由式(4)可知障碍物的斥力随着距离的减小而变得很大,由式(3)可得目标点的引力随距离的减小变得很小,这就会造成自动驾驶车辆受到的势场合力一直指向目标方向的反方向,从而使得车辆停滞无法前进到达指定的目标点。
2)局部极小值问题。引力与斥力的合力决定自动驾驶车辆的移动方向,当车辆在某一点所受到的合力为零或者合力方向与引力和斥力共线时,车辆将无法确定下一步的前进方向,可能会出现停止或者徘徊的情况。下图2中展示了两种导致局部极小值问题的障碍物分布类型,分别是“U”型障碍物、“L”型障碍物与目标点共线的情况。
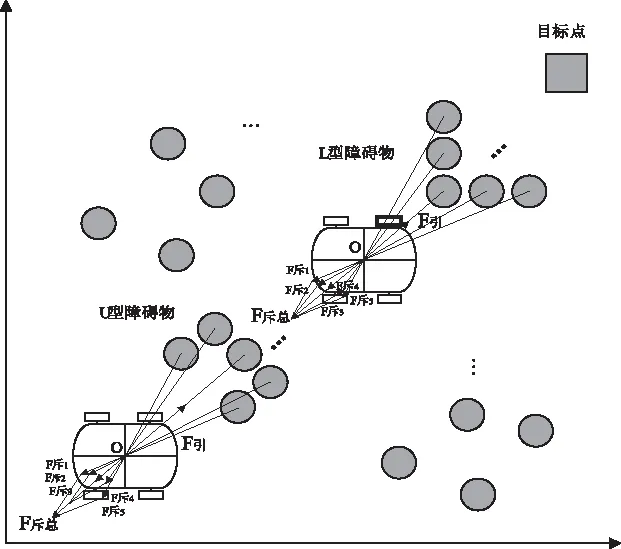
图2 自动驾驶车辆在势场中陷入局部最小值的几种情况
3 改进的势场法
3.1 引力场函数的改进
由式(3)可知目标点的引力是和车辆与目标点的距离成正比,也就是说当二者距离较远时,此时引力相当大,周围障碍物的斥力相比引力而言会较小,这可能导致车辆受到很强的引力来不及躲避障碍物与其相撞。对于引力过大的问题,对引力场和引力函数进行改进,公式为
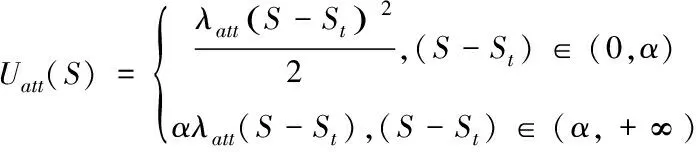
(6)
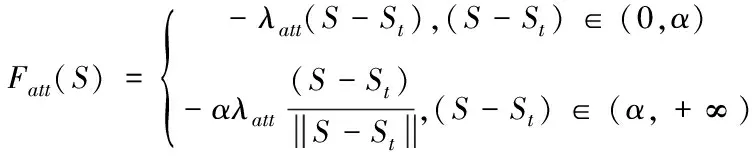
(7)
式中α为人为设定的距离阈值,也可以理解为目标点对车辆的影响距离。当车辆位置与目标点位置距离大于设定的距离阈值α时,引力则为常数。当车辆位置与目标点位置距离小于设定的距离阈值α时,可认为车辆行驶到目标点影响距离以内,此时引力同未改进前一样与二者距离成正比。
3.2 斥力场函数的改进
对于目标不可达问题和局部极小值问题,需要对传统人工势场法中的斥力势场函数进行改进,保证车辆在遇到上述几种局部极小值的情况下能够抵达并稳定在目标点,即整个势场中目标点是全局最小值。常用的方法是将车辆与目标点的相对距离的n次方引入到原有的斥力势场函数中,即(S-Starget)n为斥力函数调节因子。对于障碍物的影响距离进行分段,在不同的距离阈值采用不同的斥力,使得目标点位置的斥力为零,车辆稳定于目标点。
斥力增益系数λrep为正数,障碍物对车辆的影响距离d0,车辆与障碍物距离大于d0时不受此障碍物的影响,这里在S0与障碍物边界之间增加一个距离阈值d0/2。
当S-Sbarrier∈(d0,+∞)时,车辆处于安全区域不会与障碍物碰撞此时斥力势场和斥力都为0,S-Sbarrier∈(d0/2,d0)时,车辆处于控制区域此时障碍物产生斥力作用于车辆且线性收敛,S-Sbarrier∈(0,d0/2)时,车辆处于危险区域,当车辆进入即将发生碰撞的危险区,所受的斥力要保证其尽快远离该区域。
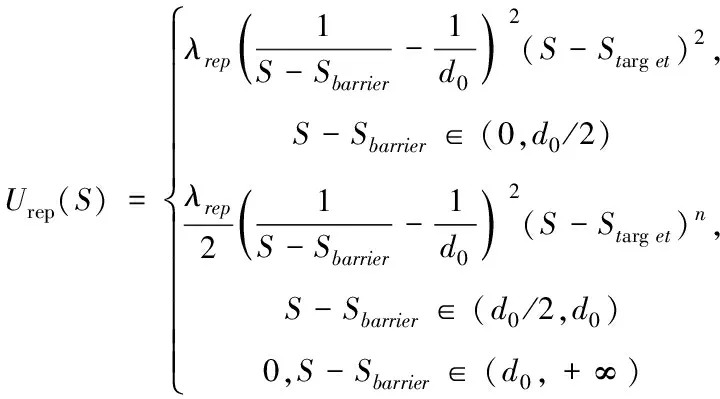
(8)
对斥力势场求负梯度,由式(8)计算得到斥力,其公式为
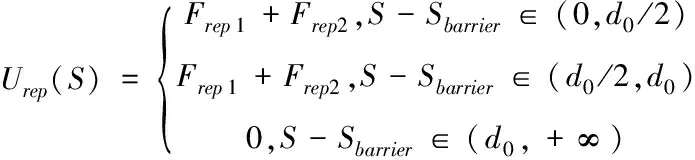
(9)

(10)
式中n可以取大于0的任意常数,Frep的两个分力为Frep1和Frep2,二者都是是障碍物对车辆的斥力分力,Frep1受力方向从障碍物指向车辆,Frep2受力方向从车辆指向目标点。斥力函数调节因子(S-Starget)n中n的取值影响到自动驾驶车辆的受力情况,故对其进行讨论以分析不同取值下Frep1和Frep2的大小。
1)n∈(0,1]
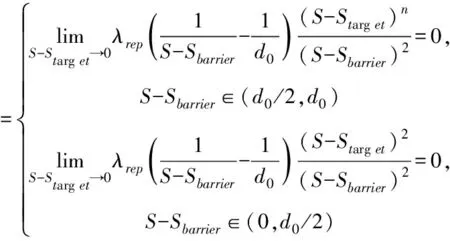
(11)
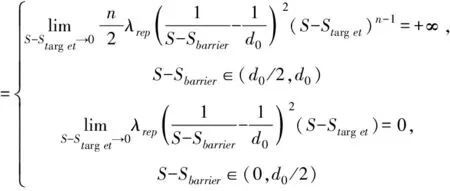
(12)
当自动驾驶车辆靠近目标位置时,无论是S-Sbarrier∈(d0/2,d0)的控制区还是S-Sbarrier∈(0,d0/2)的危险区,此时障碍物对车辆的斥力Frep1都趋于0。目标点对车辆的引力Frep2在S-Sbarrier∈(d0/2,d0)的控制区内趋于无穷大,在S-Sbarrier∈(0,d0/2)的危险区内趋于0。当n在(0,1]内,车辆处于控制区时在Frep2和Fatt的共同作用下靠近目标位置,处于危险区时只在Fatt作用下靠近目标位置。
2)n∈(1,+∞]
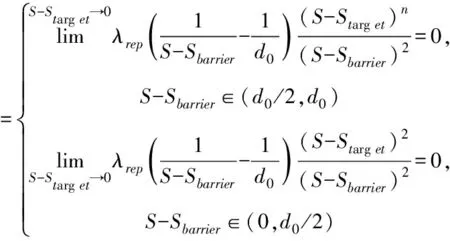
(13)
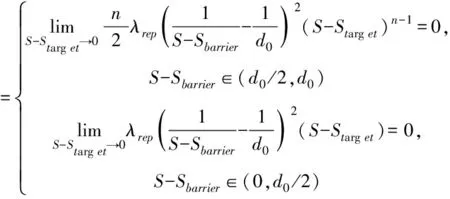
(14)
当自动驾驶车辆靠近目标位置时,无论是S-Sbarrier∈(d0/2,d0)的控制区还是S-Sbarrier∈(0,d0/2)的危险区,此时障碍物对车辆的斥力Frep1、Frep2都趋于0。此时车辆只在Fatt作用下靠近目标位置。
4 Matlab仿真分析
本文选取重庆交通大学南岸校区内障碍物环境为研究区域,起点为重庆交通大学1号门,目标点为菁园小区,黑色方框内为路径规划区域,将区域内建筑物障碍物全部抽象为圆形障碍物,计算势场力,试图规划出一条无碰撞的自动驾驶车辆路径,研究区域如图3。
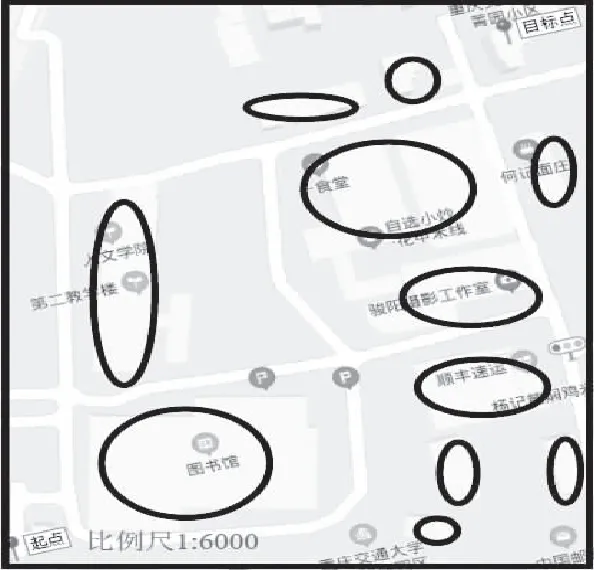
图3 重庆交通大学南岸校区1号门-菁园小区
利用 Matlab 2016a软件针对传统的人工势场法的存在的问题进行仿真,以下仿真结果是在障碍物均为静态的前提下进行的,步骤如下:
1)仿真环境设置为x轴为8、y轴为9的二维区域,起始位置设为(0,0),目标位置为(7.2,8)。引力势场增益常数λatt=1000斥力势场增益常数λrep=15。自动驾驶车辆的步长l=0.1,障碍物的影响距离p0=1。
2)计算的车辆和各个建筑物障碍,和目标点之间的与X轴之间的夹角(统一规定角度为逆时针方向)
3)根据车辆当前位置与目标和障碍物的角度,分别计算引力和斥力在x和y轴方向的分力。
4)根据引力与斥力在x轴方向的分力的合力,在y轴方向的分力的合力,确定车辆下一步的x坐标和y坐标,更新位置坐标、与障碍物和目标点的角度,记录车辆走过的点。
5)判断是否车辆达到目标点,若抵达则步骤结束,否则将重新转入步骤3)。
传统势场法下路径规划在不遇到复杂障碍物的前提下可以顺利达到目标点,本文实验则遇到了局部极小值致车辆无法抵达目标点的情况,见图4(a),对势场函数进行改进后见图4(b)。
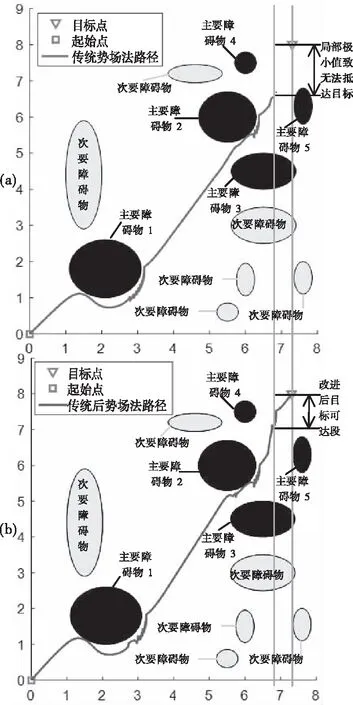
图4 传统势场法与改进势场法下自动驾驶车辆路径规划图
图4中黑色实心圆代表影响路径规划的主要障碍物,淡蓝色实心圆代表对路径规划无影响的次要障碍物。红色方形代表起始点,蓝色三角形代表目标点,红色实线代表传统势场下车辆的运动轨迹,蓝色实线代表改进后车辆的运动轨迹,传统人工势场法下,自动驾驶车辆没有成功绕开障碍物,陷入了局部极小值最终没能抵达目标点处。改进的人工势场下,车辆成功绕过障碍物避免了陷入局部极小值到达目标点位置。
对传统势场函数与改进后势场函数分别求路径过程中总势场值见图5。
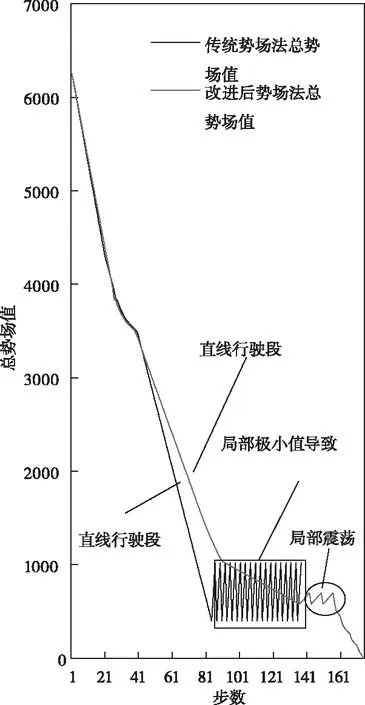
图5 传统势场法与改进势场法势场曲线图
图5为与两种方法所对应的势场曲线图,图5(a)对应传统势场法,可以看到,当车辆运行到第81步的时候,总势场陷入了局部极小值,因此车辆在此处停滞不前;图6(b)对应改进人工势场法,可以看到运行到第141步时,虽出现了局部震荡但总势场没有出现局部极小点,因此最终可以到达目标点。
自动驾驶车辆路径规划目的是为了规划出安全无碰撞且相对平滑的路径,因此这里引入路径规划的评价模型对传统势场法与改进后势场法所规划出的路径进行量化评价[23]。
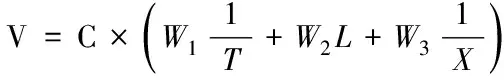
(15)
式中,V为评价值,V越大,表明规划路径的质量越高;W1、W2、W3为权重系数,且三者和为1;C、T、L、X分别为碰撞系数、转点数量、直线行驶长度以及寻路时间,这些参数的含义如下。
对于车辆规划而言,基本的要求就是不与障碍物发生碰撞,因此规定C=1为无碰撞,C=0时视为撞到障碍物路径规划失败。路径平滑度通常需要参考转折点数,转点数量越多说明路径规划的平滑度越差,反之则平滑度越好。路径的长度可以确保的情况下,直线行驶长度越长,则说明规划出的路径无需车辆保持较高的灵敏性,反之则要求车辆保持较好的转向性。路径规划时间的大小可以一定程度反映资源的消耗,路径时间越短规划的结果一般越优。
应用规划路径评价模型来评价传统势场法与改进后势场法规划出的路径,结果见表1。
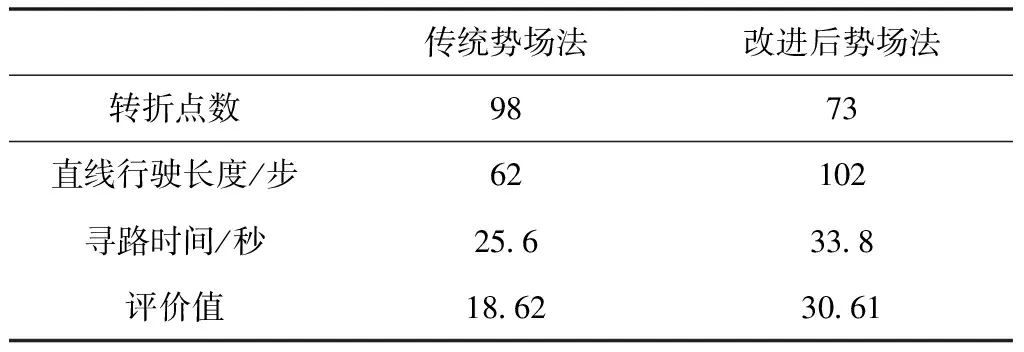
表1 两种势场法评价对比
由表1,可以明显的看出传统与改进后两条规划的路径都是无碰撞的,改进后直线行驶长度L明显变长,说明规划路径中更多是直线规划,降低了对车辆自身机动性的要求,转折点数量进一步减小说明路径的平滑度提升,寻路时间相较于传统势场法较长是由于改进后的路径抵达了目标点。最终路径评价值V 显示,改进势场函数的路径较传统势场在评价值方面提高了64%,说明基于势场函数的改进模型大大提高了路径规划的质量。
5 结论
针对传统人工势场法中当车辆距离目标点较远时引力过大斥力过小而无法避开障碍物的情况下,通过引入车辆与目标位置之间的距离阈值α,大于阈值α时引力为常数,小于阈值α时引力与距离成正比以解决避障问题。对于传统势场法中的目标不可达和局部极小值问题,本文对于斥力函数进行了改进,在改进的斥力函数中加入斥力调节因子,并对障碍物的影响范围分进行段讨论,通过设定障碍物分段影响距离点计算不同的斥力。最后以重庆交通大学南岸校区1号门为起点菁园小区为目标点,所在区域进行实地路径规划,利用Matlab2016a对自动驾驶车辆仿真的结果表明改进后的势场法有效,画出了车辆规划的路径,并对传统势场法与改进后势场法进行量化评价,结果表明改进后势场函数在评价值上提高了64%,明显提高了路径规划的质量。
