自耦变压器投入导致距离保护误动分析及改进

林国松，张 硕，权 伟，李 原

（西南交通大学电气工程学院，成都 610031）

距离保护是判别短路故障点到保护安装处的距离（或阻抗）的一种保护元件，检测被保护线路的电压、电流、相位3个特征参数的变化，是电气化铁路牵引变电所牵引网的主保护[1]。为了防止机车投入机车主变压器和AT所投入自耦变压器产生的励磁涌流对牵引变电所馈线距离保护的影响，配置了2 次谐波闭锁元件[2]。利用小波变换方法来区分线路故障及励磁涌流[3-4]。早期我国采用的韶山型电力机车为交直型电力机车，其功率因数低，负荷电流种含有大量的低次谐波，尤其是3、5、7 次谐波。而牵引网发生故障时谐波含量很小，可以通过计算综合谐波含量大小来区分远端故障和负载[2]。随着我国电气化铁路，特别是高速铁路的快速发展，交直型机车逐渐退出历史舞台，而当前的和谐号、复兴号机车或动车组均为交直交型电力机车，其功率因数高，便于调速，负荷电流基本不存在低次谐波，其中的高次谐波含量也大大减少[5]，因此当前的距离保护将综合谐波抑制功能取消。

AT供电方式牵引网的一个优点是可以直接退出AT 所进行内部设备的检修，短时间内不影响机车的运行。AT所设备检修完毕，需要投入自耦变压器，通常会出现牵引网带负荷投入自耦变压器的情况。任何变压器端电压的突然上升都有可能导致变压器铁芯保护并产生励磁涌流。励磁涌流中的非周期分量流过系统电阻会导致公共节点上的电压非周期波动，进而引起相邻变压器产生和应涌流[2]。

国内外主要对励磁涌流及和应涌流产生的机理做了大量理论研究。文献[6]指出了在励磁涌流中含有大量的2 次谐波，并分析了直流偏磁对2 次谐波制动的影响，提出对2次谐波制动判据的改进方法。文献[7-9]对电力系统中变压器和应涌流的产生进行了详细分析，和应涌流有并联和级联两种类型[9]。文献[10]对机车励磁涌流产生原因进行推导，分析了影响机车励磁涌流的因素。文献[11]对同一线路上两辆电力机车过分相产生涌流的影响进行了分析，并推导了理论公式，但并未研究机车产生的涌流对馈线距离保护的影响。文献[12-13]分析了和应涌流对电力继电保护产生的影响，以及导致差动保护误动作的原因，提出采用2、3次综合谐波闭锁避免保护误动。

本文以1 次单线AT 供电方式下的馈线距离保护误动为例，分析距离保护误动作原因，提出距离保护辅助元件的改进方案，避免该类运行检修情况下的保护误动作。

1 变电所距离保护误动作

某电气化铁路采用单线AT供电方式线路共有3个AT段，其供电示意如图1所示，其中，为T线对地电压，V；为F 线对地电压，V；为T 线电流，A；为F线电流，A。

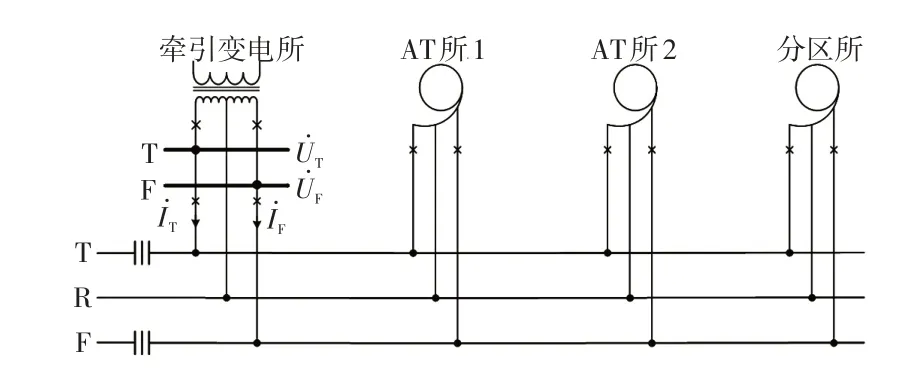
图1 单线AT 牵引网Fig.1 Single-line AT traction network

牵引供电系统的馈线保护采用距离保护，其采用如图2 所示的多边形动作特性[14]，其中，φ1为躲涌流偏移角度，取85°；φ2为容性偏移角，取-15°；φline为线路阻抗角；Rset、Xset分别为电阻整定值和电抗整定值。

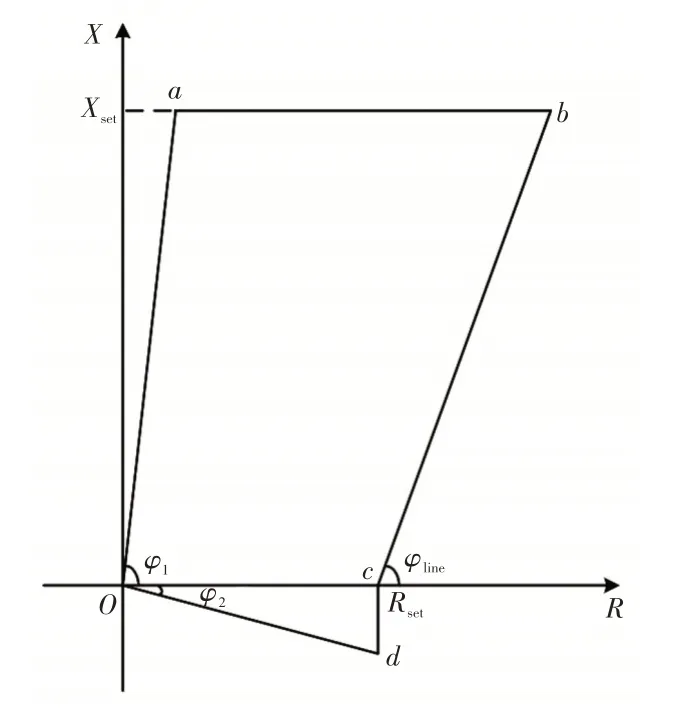
图2 多边形阻抗动作特性Fig.2 Polygon impedance action characteristics

在2×27.5 kV的AT供电方式下，距离保护的阻抗计算公式为

电抗整定值Xset按保护正常供电线路全长整定，可表示为

式中：Kk为可靠系数，取1.2；l0为供电线长度，km；l1为接触网长度，km；x0.F为F 供电线单位电抗，Ω/km；x1.F为F线单位电抗，Ω/km。

电阻整定值Rset按躲过最小负荷阻抗整定，可表示为

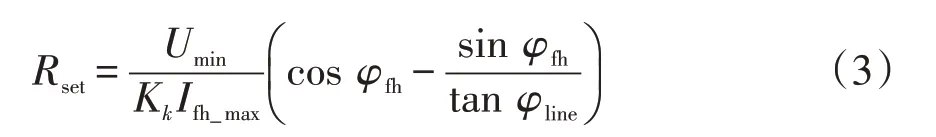
式中：Umin为正常供电时变电所T母线的最低运行电压，V；Ifh_max为正常供电时馈线的最大负荷电流，A；φfh为负荷阻抗角；φline为线路阻抗角。

在某新建运行的AT 供电方式线路上，当检修人员检修完分区所并重新将分区所的AT投入运行时，牵引变电所馈线距离保护发生误动。故障报告如图3所示。

图3 距离保护误动作报告Fig.3 Distance protection maloperation report

由图3 可知，牵引变电所距离保护配置2 次谐波闭锁功能，根据保护与实际定值对比，测量阻抗进入距离保护动作区，属于正常的保护动作。

牵引变电所馈线保护装置接收到的故障前后的电压、电流波形如图4所示。从图4可以看出，分区所自耦变压器大致在t=0.025 s 时投入，投入前电压、电流波形保持正常，投入后电流产生非周期分量和谐波，导致波形发生畸变。

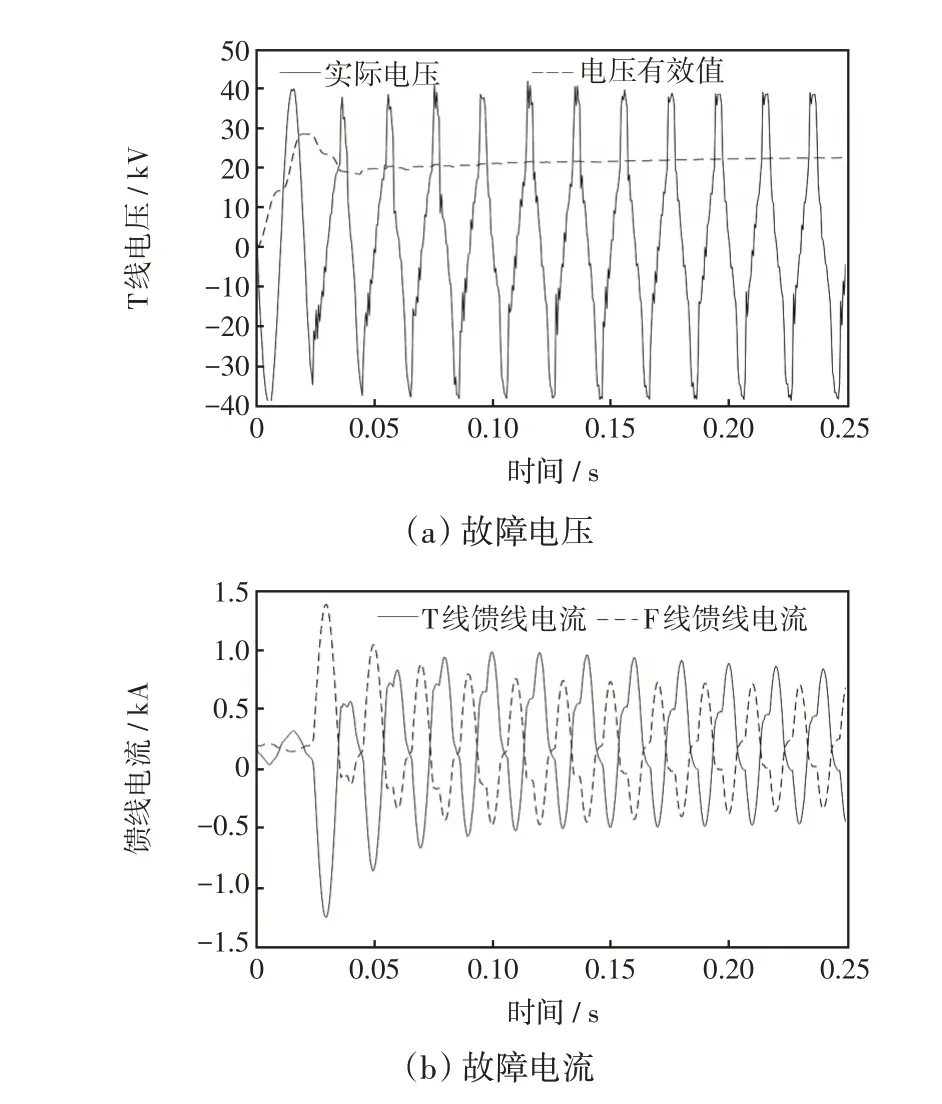
图4 馈线保护故障波形Fig.4 Fault waveforms of feeder protection

2 距离保护误动作分析

由于分区所自耦变压器空载投入时，会产生励磁涌流，励磁涌流中含有大量的以2次谐波为主的谐波电流和非周期分量电流。为了避免因自耦变压器投入导致距离保护误动，采用2次谐波闭锁辅助功能闭锁距离保护。由图3的跳闸报告可知，在距离保护启动至动作过程中，2 次谐波闭锁并未动作，导致距离保护误动作发生。

图5 为由图4（b）所示的故障电流波形采用傅里叶递推算法计算得到的2 次谐波含量曲线。可以看出，从投入自耦变压器到t=0.1 s 的时段内，2次谐波含量大于15%（见图5 中虚线），之后2 次谐波含量减小并小于15%。图6为由图4所示的故障电压及故障电流计算得到的测量电阻和测量电抗，其中虚线分别为距离保护的最小整定电阻和最小整定电抗。从图6可以看出，电阻和电抗进入了距离保护动作区。图5 中，在t=0.1 s 后，2 次谐波含量低于15%，从而闭锁功能解除，最终导致牵引变电所距离保护达到保护时限而误动。

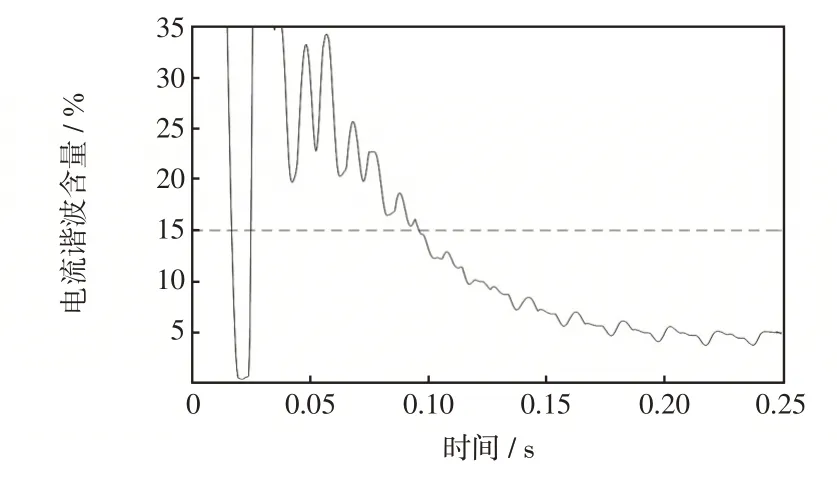
图5 故障电流2 次谐波含量Fig.5 Second harmonic content in fault current

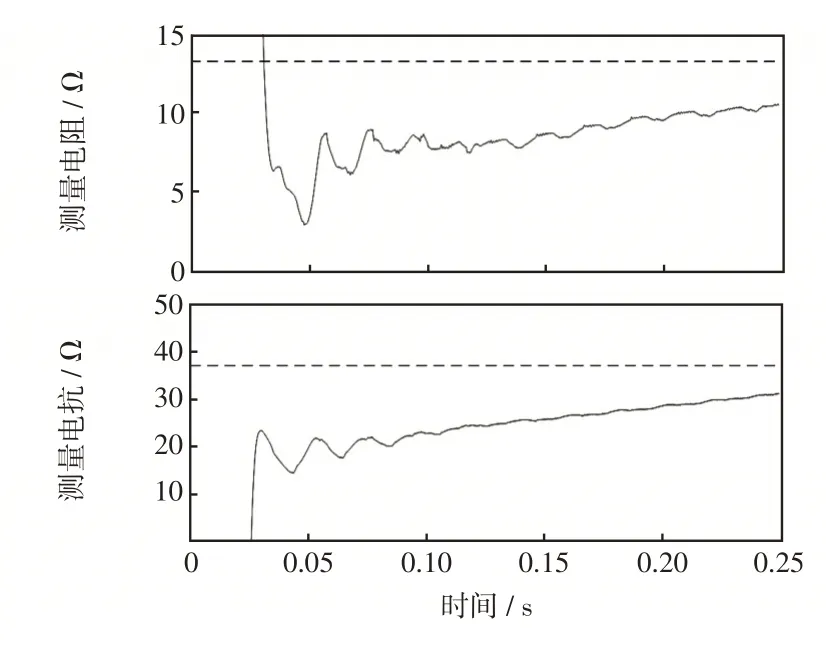
图6 测量电阻、电抗与定值关系Fig.6 Relationship among measured resistance,reactance and fixed value

从图4（b）可以看出，电流波形的第1周波为正常运行电流，表明在分区所自耦变压器投入前，牵引网中有机车取流，存在负荷电流；之后分区所自耦变压器投入，由于磁通饱和使励磁阻抗急剧减小[15]，自耦变压器产生励磁涌流，此时馈线电流应为负荷电流与励磁涌流、和应涌流的叠加。

文献[16]有详细介绍单相变压器空投产生励磁的过程。变压器空投后的磁通φ的表达式为

式中：φ0为变压器合闸初相角；φm为磁通稳态交流分量幅值；φr为铁心剩磁；R为系统电阻与变压器电阻之和；L为系统电抗与变压器漏电抗之和；ω为角频率。

在变压器空载合闸时，由于暂态磁通(φmcosφ0±φr)的存在，变压器的磁通可能在某些时间内超过饱和磁通，励磁阻抗急剧减小，造成变压器铁芯饱和从而产生励磁涌流[17]。

本次故障的和应涌流为并联和应涌流。令图2中的AT所1、AT所2和分区所的自耦变压器分别为AT1、AT2、AT3，自耦变压器AT1、AT2空载运行，分区所自耦变压器空载投入。和应涌流分析模型如图7 所示，其中US、iS分别为系统电压与电流；RS、LS分别为系统内阻抗；L1、RL1分别为第1 个AT段线路的电阻和电感；RL2、L2分别为第2个AT段线路的电阻和电感；RL3、L3分别为第3 个AT 段线路的电阻和电感；i1、i2、i3分别为流过自耦变压器1 次侧电流；R1σ、L1σ分别为AT1所自耦变压器漏阻抗；R2σ、L2σ分别为AT2所自耦变压器漏阻抗；R3σ、L3σ分别为AT3所自耦变压器漏阻抗；R1m、L1m分别为AT1所自耦变压器励磁阻抗；R2m、L2m分别为AT2所自耦变压器励磁阻抗；R3m、L3m分别为AT3所自耦变压器励磁阻抗。

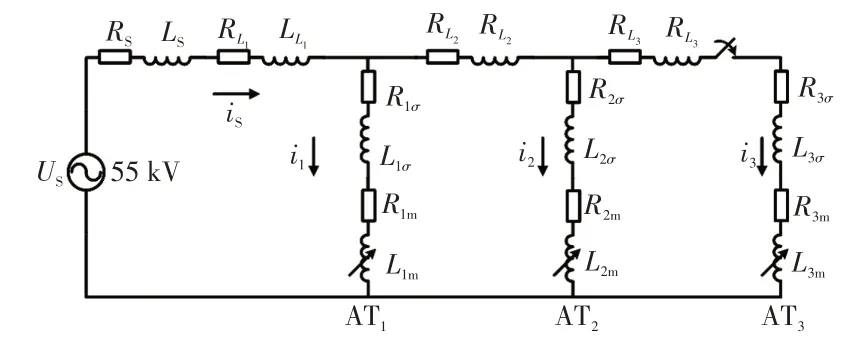
图7 和应涌流分析模型Fig.7 Analysis model of sympathetic inrush current

应用基尔霍夫电压定律和基尔霍夫电流定律可得

式中：Ψ1、Ψ2、Ψ3为自耦变压器AT1、AT2、AT3的磁链；R1、R2、R3为自耦变压器AT1、AT2、AT3的漏电阻与励磁电阻的叠加。

对式（5）进行积分，得到各个自耦变压器在1个周期T内的磁链增量为

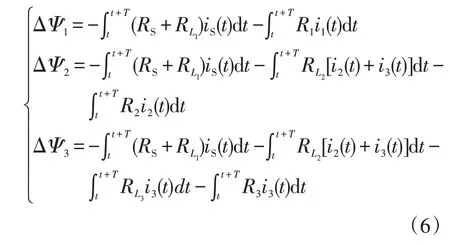
式中，ΔΨ1、ΔΨ2、ΔΨ3分别为自耦变压器AT1、AT2、AT3的磁链增量。

为了便于分析，假设自耦变压器AT3的初始磁通正偏，此时AT3自耦变压器的励磁涌流偏向时间轴的上方，而剩余AT 所的自耦变压器正常运行，AT3空投后产生的励磁涌流i3中含有大量的非周期直流分量且为正值。

由式（6）可知，ΔΨ1、ΔΨ2和ΔΨ3均为负值，即每个周期磁链都向负方向偏移。这样会使得AT3磁链逐渐减少，逐渐退出饱和，从而i3幅值逐渐减小；AT1和AT2磁链反向增加，逐渐进入饱和，从而产生涌流（即和应涌流）。

由于AT1与AT2负方向进入饱和，所以产生的和应涌流与AT3中的励磁涌流方向相反。AT1和AT2的磁链是逐渐增大的，导致和应涌流i1和i2也逐渐增大。由于和应涌流与励磁涌流方向相反，所以i1与i2中的非周期直流分量与i3相反。在某个周期ΔΨ1与ΔΨ2的积分分别为0，此时和应涌流达到最大。同样可以看出，ΔΨ2＞ΔΨ1，AT2饱和程度大于AT1，所以距牵引变电所越远的AT 所产生的和应涌流幅值越大。

由于i1、i2增大及i3减小，系统电流iS中非周期直流分量几乎为0，系统阻抗对磁链的衰减作用消失，变压器磁通增量按照下式衰减：

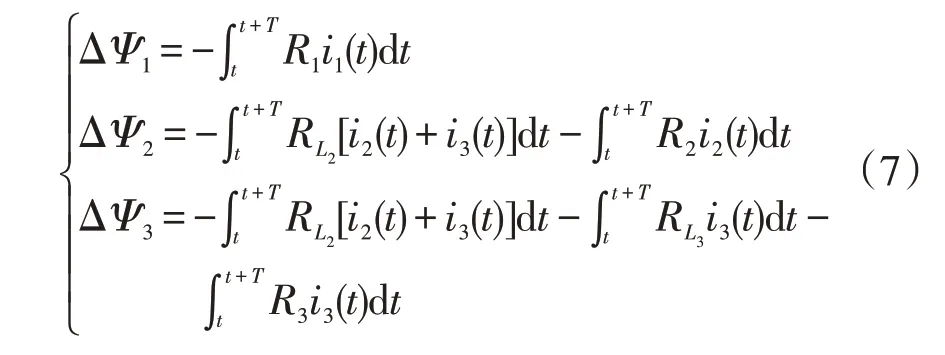
对比式（4）中的衰减时间常数，由于少了系统内阻，多台变压器导致涌流的衰减时间比单台变压器短。

从本次跳闸事件的故障电流波形可以看出，线路同时存在负荷电流、分区所自耦变压器空投产生的励磁涌流，以及励磁涌流导致其他AT 所自耦变压器产生的和应涌流。在分区所自耦变压器空投前，牵引变电所处的测量阻抗主要为线路阻抗和负荷阻抗，此时的测量阻抗主要呈现阻性，落在距离保护动作范围外，距离保护未动作。在分区所自耦变压器空投后，产生的涌流的基波电流滞后电压约为90°，呈现感性。若馈线电流为励磁涌流与负荷电流的叠加，则测量电抗会逐渐增大，测量电阻会逐渐减小，使测量阻抗进入动作区，导致距离保护误动作。

3 距离保护改进方案

为了防止距离保护在负荷电流下误动，利用综合谐波谐波含量，自动调节距离保护四边形动作特性的边界，从而提高距离保护的自适应能力。

综合谐波抑制是根据电流中谐波含量的大小自动调节距离保护的动作特性。定义综合谐波含量KΣ为

式中，I1、I2、I3、I5、I7分别为基波电流、2次谐波、3 次谐波、5 次谐波、7 次谐波。自适应保护电阻整定值与电抗整定值可以按下式整定[1-2]：

当KΣ＞0 时，自动收缩距离保护四边形阻抗特性的动作边界；只有当KΣ＞KΣ,set（KΣ,set为综合谐波含量整定值）时，才按式（9）调整距离保护的电阻、电抗整定值，以减少谐波对其造成的影响。

图8 为由图4（b）所示故障电流波形计算得到的谐波含量，可以看出，虽然2 次谐波含量随着时间推移逐渐减少，但是3次谐波和综合谐波含量仍然较高，采用综合谐波抑制可以有效避免距离保护进入动作区。

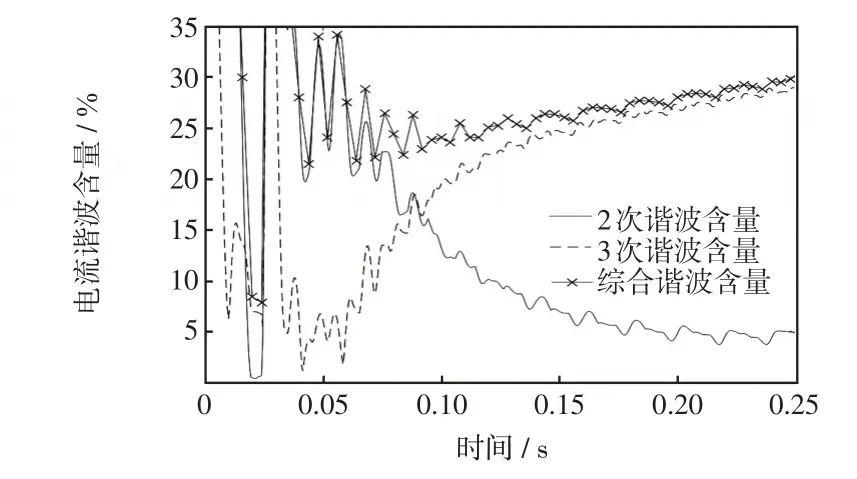
图8 故障电流中的谐波含量Fig.8 Harmonic content in fault current

一般情况下，在自耦变压器投入时，线路上负荷电流不大，2 次谐波闭锁距离保护功能可以满足绝大部分运行情况。

在牵引网故障中故障电流波形谐波含量极低的情况下，本文考虑在现有距离保护基础上，增设3次谐波闭锁功能，闭锁距离保护。3次谐波闭锁判据为

式中，Hset为3次谐波闭锁整定值，根据该线路的现场情况，以3次谐波含量等于15%作为推荐值。

4 仿真验证

通过Matlab/Simulink 搭建本次误动的仿真模型，线路采用单线AT 供电方式，共有3 个AT 段，长度分别为16 km、13 km 和13 km。仿真模型参数如表1所示。AT牵引网阻抗矩阵Z可表示为

表1 仿真模型参数Tab.1 Parameters of simulation model

（1）假设线路初始带有负荷，分区所自耦变压器剩磁为0.9 p.u.，负荷电流约为350 A。当t=0.1 s时合闸初相角为0°，此时分区所自耦变压器投入。变电所馈线电流和谐波含量仿真结果如图9所示。

对比图4、图8、图9可以看出，仿真结果与实际录波分析结果相似，验证了馈线电流近似为负荷电流与励磁涌流、和应涌流的叠加。

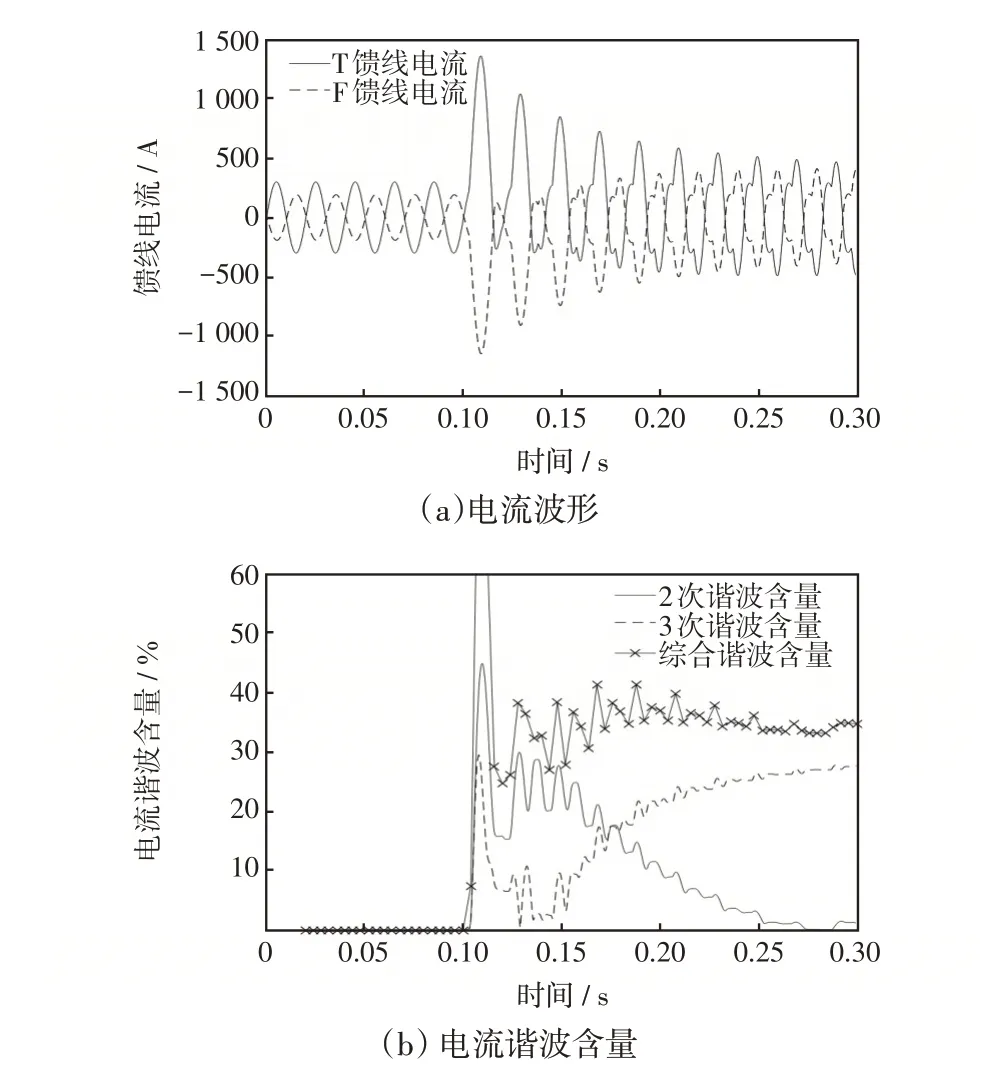
图9 带负荷时馈线电流中谐波含量Fig.9 Harmonic content in feeder current under load

（2）假设线路初始不带负荷，2 个AT 所的自耦变压器未投入（不会产生和应涌流），此时空载投入分区所自耦变压器。在牵引变电所馈线测量得到的励磁涌流谐波含量如图10所示。

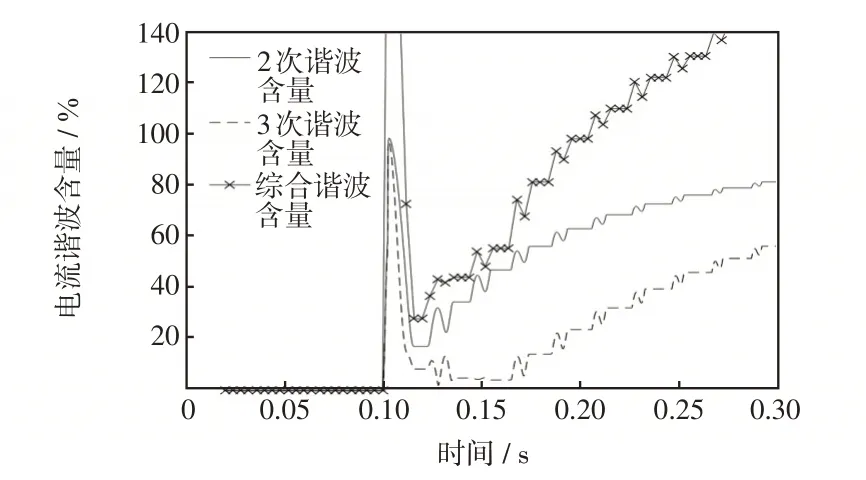
图10 励磁涌流谐波含量Fig.10 Harmonic content in excitation inrush current

从图10可以看出，励磁涌流中2、3次谐波的含量都远高于整定值，传统的2次谐波闭锁功能可以闭锁距离保护，避免误动作。

（3）假设线路初始不带负荷时，2 个AT 所的自耦变压器已经投入，此时空载投入分区所自耦变压器。在牵引变电所馈线测量得到的和应涌流谐波含量如图11所示。

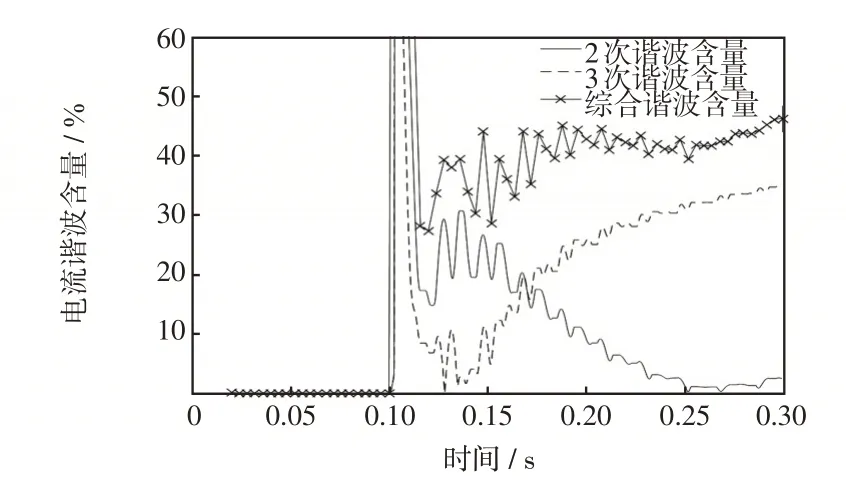
图11 和应涌流与励磁涌流的谐波含量Fig.11 Harmonic content in sympathetic inrush current and excitation inrush current

从图11 可以看出，由于分区所自耦变压器的投入产生和应涌流，使得其他AT 所自耦变压器也产生和应涌流，励磁涌流中2、3 次谐波含量丰富。在馈线电流叠加和应涌流后，波形趋近对称，2次谐波含量随着时间急剧减少，并降低到整定值以下，但3次谐波含量仍很高。在线路带负荷后，此时馈线电流近似为负荷电流与励磁涌流、和应涌流的叠加，进一步导致2次谐波含量减少，但3次谐波含量减少较小且高于整定值。这样，采用3次谐波闭锁功能可以闭锁距离保护，避免误动作。

在变压器合闸瞬间，由于铁芯内的磁通不可突变，此时会产生1个非周期磁通以使铁芯磁通维持不变。当变压器合闸相角不同时，变压器所产生的励磁涌流大小不同，进而会影响和应涌流的大小。在带负荷情况下，随着负荷视在功率增大、功率因数减小，和应涌流幅值变小，出现时间延后[18]。

在不同合闸角度及负荷电流情况下，对比改进前后距离保护的动作情况。假定线路负荷电流分别为350 A、500 A，分区所自耦变压器剩磁为0.9 p.u.，仿真时间为0.5 s，t=0.1 s时以合闸相角分别为0°、30°、60°、90°进行合闸。对2、3 次谐波闭锁时间进行分析，用来对比改进前后距离保护的动作情况。距离保护动作情况如表2 和表3 所示，其中，φ0为分区所自耦变压器合闸初始相角；T2为2次谐波闭锁时间；T3为3次谐波闭锁时间；TZ为测量阻抗进入保护动作区时间。

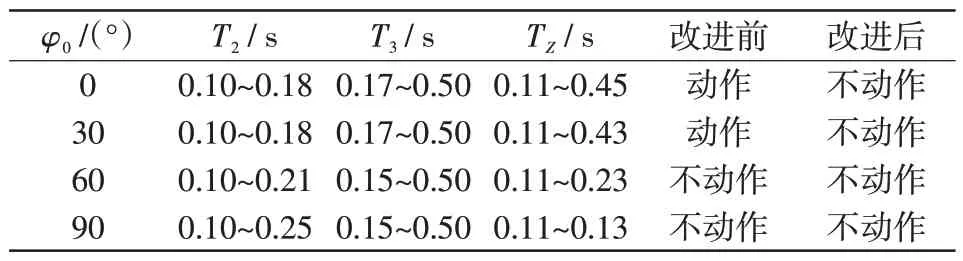
表2 在负荷电流为350 A 下的距离保护动作对比Tab.2 Comparison of distance protection actions under load current of 350 A

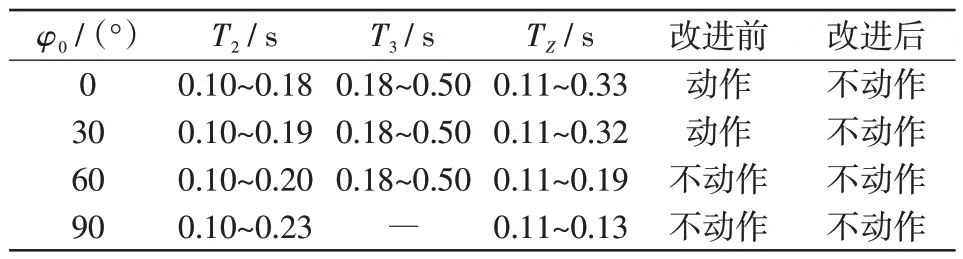
表3 在负荷电流为500 A 下的距离保护动作对比Tab.3 Comparison of distance protection actions under load current of 500 A

从表2 和表3 可以看出，当负荷一定且合闸角度较小时，2 次谐波闭锁时长不能完全避免距离保护误动，但3 次谐波闭锁时间始终较长，可对距离保护进行闭锁从而避免误动。当负荷一定且合闸角度较大时，2次谐波闭锁时间增加，测量阻抗进入动作区时间减少，改进前后均可避免误动。可见，在较大合闸角度和较大负荷时，即使3次谐波闭锁未动作，但是2次谐波闭锁时间增加可完全避免距离保护误动。对比表2 和表3 可知，在同一合闸角度下，由于负荷电流增大、和应涌流幅值减小，出现时间延后，使得2、3 次谐波含量与闭锁时间均减少，但是因为测量阻抗进入动作区时间也减小，甚至小于距离保护动作时限，这样改进后的距离保护仍可避免误动。

5 结语

本文根据AT 供电方式下距离保护误动作情况，分析了故障跳闸时变电所馈线电压、电流的特征。牵引网存在负荷电流、励磁涌流与和应涌流三者电流的叠加。馈线电流中2次谐波含量小于整定值，从而2次谐波闭锁时长不能完全躲避掉涌流与负荷的叠加，导致距离保护误动。现场故障波形分析和理论分析表明，在牵引网存在负荷的情况下，投入自耦变压器时，3次谐波的含量较高的原因，从而提出了基于3 次谐波闭锁距离保护改进方案。基于Matlab/Simulink仿真验证了改进方案的可行性。

需要指出的是，当前距离保护装置均没有配备本文所提3次谐波闭锁功能，有些距离保护装置还取消了综合谐波抑制功能。在此情况下，建议运营单位在牵引网无负荷时投入AT所或分区所的自耦变压器，避免因涌流电流与负荷电流的叠加落入距离保护动作区，造成距离保护误动。