多元统计分析思想在地球物理与地球化学勘查中的应用

徐龙生，路 瀚，黄天统，苑东洋

(1. 核工业二三〇研究所，湖南 长沙 410000； 2. 中国地质大学(武汉)地球物理与空间信息学院，湖北 武汉 430074； 3. 中国冶金地质总局西北地质勘查院，陕西 西安 710119)

0 前 言

多元统计分析是从经典统计学中发展起来的一个分支，是一种综合分析方法，它能够在多个对象和多个指标互相关联的情况下分析统计规律，很适合地球科学研究的特点。在地质科学中应用比较多的有相关分析、回归分析、聚类分析、多元方差分析、主成分分析、因子分析、判别分析与聚类分析等。

统计分析是系统论述统计理论和方法的科学，因其具有较好的实用性，可应用到地球物理、地球化学研究中。许多学者[1-6]将多元统计分析应用到地球物理、地球化学、水文地质、煤炭地质、石油地质等地球科学领域中，并取得了非常好的效果。通过统计方法在地球物理与地球勘查中的应用，展现出统计方法在相关地球物理与地球化学研究中取得的成果，同时验证多元统计方法的优越性和应用广泛性。

1 多元统计分析概述

目前的多元统计分析作为一类应用广泛、新兴的数据处理方法，在各个学科中均得到较好应用，其并没有展现出复杂系统中结构形成和演化的动力学特性，亦没有探索出复杂系统中的地球物理学与地球化学原理[7]。

应用多元统计分析方法(回归分析、相关分析、聚类分析、因子分析、判别分析)基本思想是将研究区所有局部异常(样品)进行分类，根据分类后某些异常对应于某些已知矿(已知样品)，则同类中其他异常(未知样品)也是该已知矿母体的反映,从而作出成矿预测[8]。

2 多元统计分析方法原理

2.1 回归分析方法

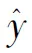
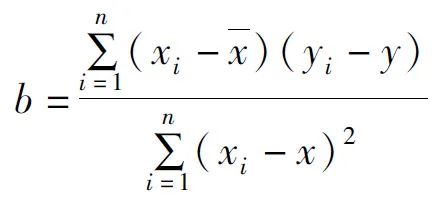
(1)

式(1)中：n为样本量，xi、yi、x、y分别为两个变量的观测值和均值。若b→0，表明两变量是正相关；若b<0，表明两变量是负相关。另外，b的大小还表明若变量x发生一个单位变化时，变量y的变化量对于总体回归系数为0的原假设，也可以用t统计量进行检验。当t检验显著时，拒绝原假设，即总体回归系数不为0，两个变量呈线性关系；当t检验不显著时，不能拒绝原假设，两个变量不是线性相关。

在研究重力异常和高程的关系时，常常用回归分析来研究高程对重力布格异常的影响。在高海拔地区，尤其是青藏高原地区这种影响特别明显，故而一元线性回归分析就有很重要的意义。

2.2 相关分析方法

相关分析是研究两个或两个以上处于同等地位的随机变量间相关关系统计分析的方法。相关分析与回归分析之间的区别：回归分析侧重于研究随机变量间的依赖关系，以便用一个变量去预测另一个变量；相关分析侧重于发现随机变量间的相关特性[9]。相关分析在地质矿产勘查中，尤其在地球物理、地球化学等方面都有广泛应用。

相关系数是按积差方法计算，是以两个变量与各自平均值的离差为基础，通过两个离差相乘来反映两个变量之间的相关程度。重点研究线性的单相关系数，确定相关关系的数学表达式，确定因变量估计值误差的程度[10]。

相关分析现象之间的相互联系，经常表现为一定关系，其中一个或若干个起着影响作用的变量用x表示，与之相关的另一现象变量用y表示。通常用相关系数r表征这两个量的相互关联程度，计算公式[11]:

(2)

相关系数r的取值范围：-1≤r≤1。r的绝对值愈大，变量间的等级相关程度愈大[1]；r>0为正相关，r<0为负相关；|r|=0表示不存在相关关系；|r|=1表示完全线性相关；0<|r|<1表示存在不同程度线性相关。

在地球科学研究应用中，|r|≤0.3为不存在线性相关；0.3<|r|≤0.5为低度线性相关；0.5<|r|≤0.8为显著线性相关；|r|→0.8为高度线性相关。

2.3 统计分析方法

统计分析方法就是运用数学思维方法，构建一定的数学模型，分析通过各种途径获取的不同数据及资料进行数理统计研究，形成定量解释成果。统计分析方法是广泛使用的现代科学方法，是一种较科学、精确和客观的测评方法。

成秋明院士提出多重分形与地质统计学方法用于勘查地球化学异常空间结构和奇异性分析。勘查地球化学和地球物理场的局部空间结构变化性包括空间自相关性以及奇异性，前者可通过地质统计学中常用的变异函数来实现；后者可用多重分形模型进行刻画，具有自相似性或统计自相似性的多重分形分布的奇异性可以反映地球化学元素在岩石等介质中的局部富集和贫化规律[2]。而多重分形插值和估计方法可以同时度量以上两种局部结构性质(空间自相关性以及奇异性)，不仅能够进行空间数据插值，同时还能保持和增强数据的局部结构信息，对于地球化学和地球物理异常分析和识别具有巨大的引用价值[12]。

因此，地统计学近年来成为空间分析的重要工具,其应用领域广泛分布在自然科学的众多领域[13]。

3 地球物理勘查中的应用实例

3.1 相关分析法在山西平顺重力地形改正中的应用

物探工作中地形对重力异常的影响不容忽视。地形的隆起或是凹陷，将导致重力异常图在形态上的直接变化，影响对异常的客观解释。

将布格重力异常和地形两个物理量进行相关分析，可用来反映研究区内地形起伏对重力异常的影响情况，地形改正是否完全以及改算方法是否完善[14]。这里所需要的重力异常数据文件和高程数据文件必须是以相同的网格间距网格化的、具有相同横纵坐标的“*grd”网格化文件。

山西平顺县龙溪镇新天岭矿业铁矿勘查区地处太行山断隆南部，太行山复式背斜西翼，最高海拔1 782 m，最低海拔1 393 m，在研究区约8 km2的范围，地形高程变化范围约389 m，地形较为复杂(见图1a)，地形改正是研究区较为重要的工作。本次地形改正使用收集的1∶10 000的DEM高程数据进行中区地改，远区地改使用1∶50 000的DEM高程数据，最大限度地减小地形变化对重力场的影响，增强地改效果。研究区南北部是重力异常富集区，因而在研究区南北部是各截取一个剖面(见图1b)分别进行了5 km和20 km的地形改正，用于探讨本次地改效果(见图2)。

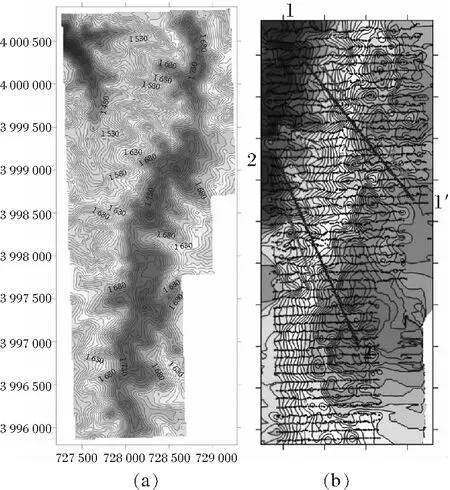
图1 研究区海拔高程地形(a)、研究区地改剖面位置(b)

图2 1-1′剖面地改综合异常(a)、2-2′剖面地改综合异常(b)

经过地形相关分析可知，1号和2号剖面地形线(黑色线)均显示单边上行的形态，不同半径(5 km和20 km)的地形改正曲线均反映出地形改正的削高填低的作用，而且小半径地改的这种作用更明显，因此20 km地改半径后的布格重力异常包含了更多区域重力场，其剩余异常特别是重力高的范围相对较大，反映了更多的深部地质体的作用。由前述地质成矿的描述可知，研究区矿体和岩体范围和埋深有限，矿体小、多为豆荚状或透镜体，结合两个剖面的地改计算对比结果来看，选取5 km的地改半径比较合适。从研究区来看，研究区地形图(见图1a)出现东西两侧地势低、中部明显隆起的形态，经过地形改正及其他各项改正后的布格异常图显示了自西向东逐渐升高的重力场特点，地形和布格重力场没有出现明显的相关性，本次地改较为有效地消除了地形对重力场的影响，而且经过半径为5 km地形改正后的布格重力异常，更多地显示出浅部地质体的重力场，压制了深部因素引起的重力场。

根据布格异常与地形的相关分析，远区地改做5 km的改正半径较为合理。背景重力场整体是东高西低，平均场值为-1.8×10-5m/s2，变化范围为-2.8×10-5～0.8×10-5m/s2。研究区布格重力场等值线见图3。

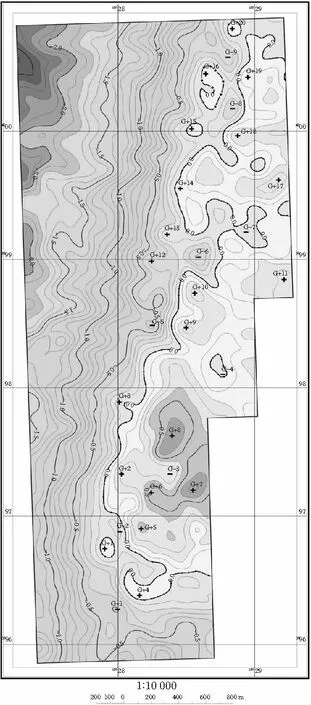
图3 布格重力异常

相关分析得到重力场具有显著特点，中部重力场以梯级带形式将研究区重力场一分为二，西低东高，单向递增，重力异常梯级带走向基本是北北东走向。由前述可知研究区发育轴向为北北东走向的背斜，背斜轴部大致位于重力梯级带的东部。这种重力场特点显然反映出了研究区的背斜地质构造形态。西部重力低是倾向为西的背斜西翼的反映，体现出夹持在第一和第二岩浆岩带之间的向斜构造形态；东部重力高则反映出倾向东的背斜东翼，但东部整个重力高值区很明显具有南北两种形态的重力场，南部异常形态较为规整，赋值也高，可以看作一个较为完整的异常；北部异常较为凌乱赋值也相对低，基本属于低缓异常，突出了背斜东翼南北的地质构造包括矿产地质等差别较大。重力场最低处位于研究区西北角，最低值为-2.8×10-5m/s2，反映出向斜构造向西延伸，其核部位于研究区外围的西侧；位于研究区东南部的重力场最高值为0.8×10-5m/s2，重力值最高处周围的重力场为环形异常，多个局部异常等值线圈闭范围较大，是研究区异常值变化最为剧烈的部位，位于铁矿05、06井口处及其以北地区，很明显是研究区已知矿体的体现。

3.2 统计分析法在青海某铅锌矿勘查中岩石物性研究应用

重力勘探是基于密度差异而进行的，掌握研究区内各地层及岩石的密度特征是重力解释与推断工作的基础。研究区岩石种类较多，主要以矽卡岩为主，其次为大理岩、二长花岗岩等。工作期间未对岩性开展密度样采集工作，主要对矿化的矽卡岩进行了系统的密度样采集工作，对不同岩矿石的不同地球物理参数进行统计分析。

应用多元统计分析方法，主要用统计分析、正态分布等方法，综合统计表中的统计数据分析，绘制了物性参数统计曲线图(见图4)，铁多金属矿矽卡岩和磁铁矿矽卡岩磁性强高于其他岩石，矽卡岩性矿体存在高磁特性。研究区基本以古生界地层为主要目标地层，最老的志留奥陶系滩间山群(OT3)至最新的二叠系打柴沟组(P1-2d)，老地层的花岗岩基本具有无磁性、低极化率、高电阻率、低密度的特性，只有电性参数与矽卡岩矿石头一致，其他均不一样。而重点地层上石炭统缔敖苏组(C2d)是矽卡岩矿化的重点层位。整个底层从老至新，磁性从无到强，电阻率从高到低，密度由低至高，综合来看，整体体现了青藏高原岩石圈板块具有轻壳重幔,软壳硬幔,热壳冷幔的地球物理特征。

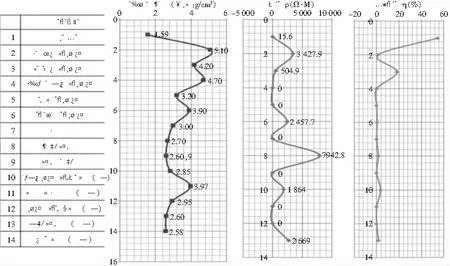
图4 研究区电阻率、密度、极化率的平均值

综上所述，牛苦头地区的矽卡岩型矿床具有“三高一低”的物性特征，即强磁特征、高密度、高电阻率、低极化率，为找矿提供了岩矿石物性基础。

3.3 线性回归分析与相关分析在西藏大比例尺重力勘查中的应用

3.3.1 重力异常与测点高程的相关性分析

采用一元线性相关分析法，对研究区布格重力异常与测点高程进行了相关分析。重力异常与高程之间的关系一般用线性回归方程表示为:

G=k×H+b

(3)

式(3)中：G为重力异常值；H为海拔高程，m；k为回归方程的斜率。它反映重力值(G)对高程(H)的敏感程度。k为正，说明高度改正值大于布格改正值，或密度改正值小于中间层实际的平均密度改正值2.67 g/cm3；k为负，则高度改正值小于布格改正值，或密度改正值大于中间层实际的平均密度改正值2.67 g/cm3。b为方程的截矩，反映整个地壳内物质平均密度的相对(相对于其他块体)大小。回归方程的可靠性用相关系数R表示。

3.3.2 重力场与高程的相关性分析及地质意义

布格重力异常与高程的统计分析(见图5)，从一个方面反映了地壳内的结构特征，为推断解释提供统计信息。图5为中间层密度2.67 g/cm3，高度起算面不同布格重力异常值与高程相关性散点图，图5a为改正到大地水准面的布格重力异常值与高程回归分析散点图，二者为正相关，斜率0.20，相关系数为0.64，截距为-506.513；图5b以罗布莎重力基点为改算点(4 219 m)的布格重力异常值与高程回归分析散点图，二者为负相关，斜率-0.003，相关系数为-0.14，截距为-505.630；图5c是以研究区内乃东县重力基点为改算点(3 522 m)的布格重力异常值与高程相关分析散点图，斜率-0.001，相关系数为-0.03，截距为-558.055，说明高程与重力场值不相关，布格重力异常值不受地形起伏的影响，说明重力场值与近地表地层岩石密度不均匀性关系密切。

通过以上线性回归分析及相关分析，结合研究区内地层、岩体的出露情况及研究区内采测的地层岩(矿)石、钻孔岩芯密度统计结果，结合地形地貌特征，形成以下结论：①布格重力异常与高程相关性分析，其相关系数、斜率、截距的大小，与进行统计现象变量的数量的多少及现象变量选取区段有关。只改变现象变量的数量和现象变量中H的高度段，得到的结果相差很大，布格重力异常与高程为呈显著线性相关，进行比较，可以看出异常范围、形态大体一致，说明布格重力异常是近地表地层岩石密度的不均匀性引起的[16-17]。②从宏观考虑，依据重力场特征，重力场分区、断裂构造划分、岩体圈定等使用的布格重力异常数据，为《区域重力调查规范》(DZ/T 0082—2021)中的计算公式计算的布格重力异常值，中间层改正密度采用2.67 g/cm3，绘制重力基础图件，及重力位场转换图件；③针对异常区重力剖面查证和小范围内的高精度重力调查，结合研究区内地层、岩矿石密度资料，采用《大比例尺重力勘查规范》(DZ/T 0171—1997)中的计算公式计算布格重力异常值，中间层改正密度采用2.80 g/cm3，以罗布莎重力基点(4 219 m)为改算点(见图6)，绘制相应的基础图件和位场转换图件。

多元统计分析在高海拔地区、大区域、大比例尺地球物理异常解释中具有必不可少的关键作用。

3.4 相关分析在祁连山小比例尺重力解释中的应用

布格重力异常在高原山区和平原区通常为负值，海洋区为正值，即布格重力异常和地形高程呈负相关。本研究区南北横跨祁连山区，地形起伏大，因此以构造特征为主，结合平均海拔高程及地形起伏程度，将研究区分为四个区域分别进行布格重力异常与高程关系的统计分析(见图7)。

图7 布格重力异常与高程相关分析

通过相关性分析统计研究，得出以下3个结论：①布格重力异常与高程为负相关，由北向南，布格重力异常与高程负相关系数分别为-0.655、-0.690、-0.534、-0.481，其绝对值不断减小，说明布格重力异常与高程相关程度在研究区北部较南部紧密，南部布格重力异常可能与应力或岩石圈异常密度分布之间的关系更加密切；②自空重力异常与高程为正相关，各区域相关系数都大于0.5，为紧密相关；③各区域曲线斜率不同，反映各区块地壳内部结构不同，物质密度分布不均匀[18]。

4 吉林省汪清县后河西阳地球化学勘查中的应用

地球化学找矿现已发展成为寻找残坡积层下隐伏矿床的一种有效的勘查地球化学方法。在地球化学测量实际工作中，因测试元素较多造成测试数据繁杂庞大，对土壤地球化学异常特征总结及解释评价带来诸多不便，从而影响找矿效果。因此，利用数学地质中的数理统计基本原理，对土壤样品测试的数据进行多元统计分析，对相关元素组合分类，探索影响地球化学异常特征的主要因素，可有效排除地球化学异常中的干扰因素，得到成矿指示元素组合特征，再结合研究区地质特征进行筛选，最终提取最佳元素组合异常[19]。

元素组合特征是地球化学特征中特别重要的一个方面。将勘查区土壤地球化学测量因子分析结果经过方差极大旋转获得正交旋转因子矩阵，正交旋转因子载荷矩阵可以使各元素在某因子上有较高载荷，而在其他因子上只有较小的载荷，使每个因子的元素组合更加明显，地质意义更加清楚。同时进行R型聚类分析，反映元素的共生组合关系。本次报告使用SPSS软件对土壤样品各元素进行因子分析与聚类分析。

4.1 因子分析

利用SPSS软件对地球化学元素数据进行统计分析，采用主成分提取，使用有Kaiser标准化的正交旋转法，旋转在4次迭代后收敛，采用3个因子正交旋转因子矩阵,根据研究区域的元素分布特征与地质综合因素，确定元素组合因子得分低限值绝对值>0.5。元素相关矩阵见表1，正交旋转因子矩阵见表2。

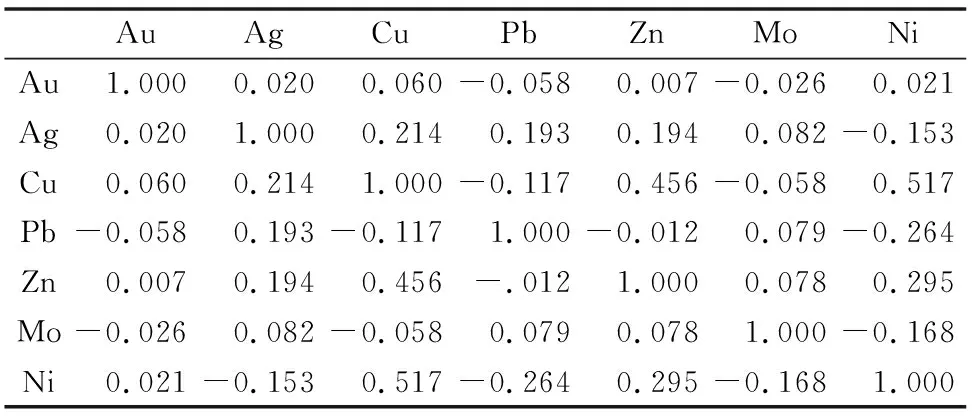
表1 元素相关矩阵值向量间的相关性

表2 正交旋转因子矩阵

由表2可以看出，3个因子基本反映了研究区元素组合特征及成矿作用特点。因子1：Cu-Ni高温成矿元素组合和Cu-Zn中温成矿元素组合，推断与勘查区南部出露的玄武岩体有关。因子2：Ag-Pb中温成矿元素组合，可能与花岗斑岩脉体侵入有关。因子3：Au单独元素组合，应与浅成低温热液矿化作用有关，且成矿期单一，可能只受到一次主要成矿热液活动影响。

4.2 R型聚类分析

利用SPSS软件进行R型聚类分析(系统聚类分析)，方法采用组间连接，度量标准采用距离的平方。

从勘查区元素的R型聚类分析结果(见图8)可以看出，当X轴(距离平方)选取16时，可分为3簇。第1簇：Pb-Mo-Ag组合，这3种元素共生可能与脉岩侵入有关；第2簇：Cu-Zn-Ni为一组中高温组合，其富集主要与玄武岩有关，在有利区块具有富集成矿的可能；第3簇：Au与其他元素组相关性表现较弱。

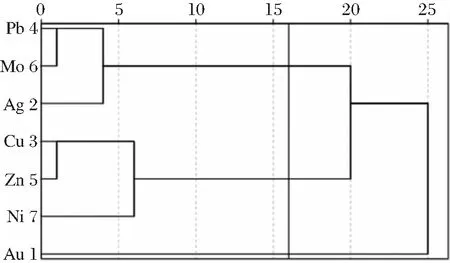
图8 R型聚类分析

综合研究区土壤测量因子分析和聚类分析结果，将研究区7个元素划分为3个元素组合。①中高温成矿元素组合：Cu-Zn-Ni；②中温元素组合：Pb-Mo-Ag；③Au与其他元素亲和性较差，呈独立因子组合。对研究区所有地球化学元素的含量进行统计分析，计算出平均值、变化系数、标准离差及富集系数等各项地球化学指标，了解区内各元素的分布与变化规律。平均值是一个集中性参数，反应勘查区各元素含量的总体水平；标准离差与变化系数均为离散型参数，反应样品含量的离散程度，但变化系数为相对参数，可用于不同元素之间对比；富集系数为平均值与地壳元素丰度的比值，能反应元素在区域上的分散、富集规律。

5 结 论

多元统计分析方法有很多，在各个学科都得以广泛应用，尤其在地球科学中也有着重要的应用价值。通过前面的研究主要形成以下几个方面的结论。

1)地球物理勘探工作中研究区及外围地形对布格重力异常的影响不容忽视，地形的隆起或者凹陷，都将引起布格重力异常曲线图在形态上、走向上、异常圈闭直接变化，影响到研究者对异常从客观上的解释，线性相关分析方法有着不可取代的积极作用。

2)岩石地球物理数据统计分析过程中，统计分析、相关分析与正态分布有很不错的效果，若结合专业分析处理软件，将能够对岩矿石地球物参数在横向上、纵向上都有很明显效果，分析结果对地球物理异常解释至关重要。

3)重力资料数据处理中，相关分析、回归分析在布格重力异常与高程的关系分析、中间层改正的密度选取都是一个必经过程，分析结果对重力异常最终数据改正值的选取，异常结果是否合理，都具很重要的作用，尤其在青藏高原的大比例尺，其余地区的小比例尺重力工作中，应用相关分析、回归分析选取中间层密度，以及高程改正起点的选取都将决定解释的精度和准确性。

4)在地球化学勘查中运用因子分析、聚类分析、统计分析、相关元素分析等统计方法，辅助SPSS统计软件，结合勘查异常区地质及构造特征，可以获取矿化特征的元素共生组合因子，依据异常特征及组合因子研究成矿特征和预测成矿规律。

5)实际工作中依据研究区地球化学数据相关分析、聚类分析和因子分析成果，揭示研究区地质异常中元素共生组合规律，这将是判断矿体剥蚀程度及成矿重要指示元素。利用这些组合异常特征，进而预测成矿特征和规律。