基于门控循环神经网络的 客运站客流预测
2022-09-27张亚伟陈瑞凤刘小燕
张亚伟,陈瑞凤,刘小燕
(中国铁道科学研究院集团有限公司 电子计算技术研究所,北京 100081)
0 引言
客流是铁路运输组织的基础和关键因素,掌握客流的现状和变化趋势对分析铁路运营计划、营销策略和售票情况具有重要意义[1]。特大型客运站如北京南站、郑州东站、西安北站在高峰时期的日发送客流量超过20万,如果没有做好正确的客流应对措施,会造成车站客流拥塞,阻碍进站检票通道,甚至会造成车站运行瘫痪。因此,提前预知客运站客流量可帮助客运人员掌握车站客流动态规律,从而及早制定客流疏散策略,如调整进站检票通道个数、候车厅客流转移等。提前预知进站客流也可以帮助旅客提前掌握客站的拥挤程度,进而合理安排出行方式和出行时间。
铁路客流量的数据集为时间序列集合。时间序列的特点包括:①趋势性。即某个变量随着时间进展或自变量变化,呈现一种比较缓慢而长期的持续上升、下降、停留的同性质变动趋向,但变动幅度可能存在差异。②周期性。某因素由于外部影响随着自然季节的交替出现高峰与低谷的规律。③随机性。个别为随机变动,整体呈统计规律。传统的时间序列预测法包括移动平均法、自回归模型、自回归滑动平均模型、指数平滑法等,该类方法对平稳、非白噪声特点的数据预测有较好的效果,然而在处理铁路客流量这种有突发性波动的数据时往往预测效果欠佳。近年来,基于深度学习网络的方法被提出和实践,比传统方法速度更快、预测更准确。循环神经网络(RNN)是一种对序列数据进行建模和预测的神经网络,并且是深度学习领域中非常重要的模型。它克服了传统机器学习方法对建模数据的诸多限制,广泛应用于多种任务中,如语音识别、机器翻译、文本分类、时序数据预测等存在序列依赖关系的场景。循环神经网络可以将神经元某时刻的输出再次作为神经元的输入,由于网络结构中的参数是共享的,这也大大提高了训练性能,同时使模型可以应用到不同长度的数据中[2]。由于RNN存在梯度消失和梯度爆炸的问题,改进的循环神经网络长短期记忆网络(LSTM)被提出,它能够让信息长期保存,成功解决了RNN的缺陷问题,成为当前最流行的RNN改进方法。研究使用LSTM的一种变体门控循环神经网络(GRU),较LSTM网络的结构更加简单,同时也可以解决RNN网络的长程依赖问题。
1 门控循环神经网络模型
1.1 RNN模型
RNN网络结构的特殊性在于对于输入RNN结构的信息具有记忆性。对于输入的序列,它的前一刻和后一刻是有关系的,从而使RNN结构具有记忆功能。RNN层级结构如图1所示[3]。与传统全连接神经网络模式一样,由输入层、隐藏层、输出层组成。不同之处在于隐藏层节点有一个自我循环输入,循环节点数与隐藏层节点数相同,该节点实现记忆功能。
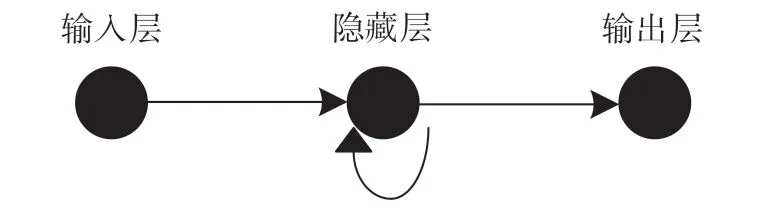
图 1 RNN层级结构Fig.1 RNN layer structure
隐藏层节点结构如图2所示。xt-1,xt,xt+1代表前一刻、当前时间、下一刻的输入值,W为权重值,U为当前输入的权重值,V为输出样本权重值,St为样本值在t处所存储的记忆值。St表达式如公式 ⑴ 所示。
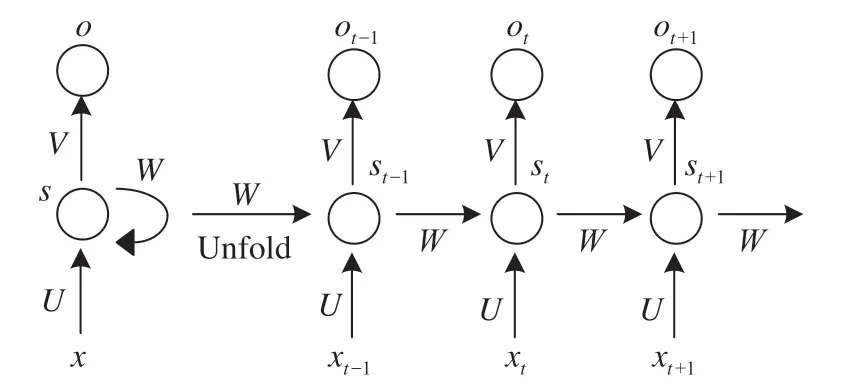
图 2 隐藏层节点结构Fig.2 Node structure of hidden layer
在t= 1时刻,一般初始化输入S0= 0,随机初始化W,U,V。计算公式如公式 ⑵ 至公式 ⑷ 所示。其中,f,g为激活函数。f一般为sigmoid,tanh,relu函数,g一般为softmax函数[4]。

以此类推,得到最终的输出如公式 ⑸ 至公式⑺ 所示。

1.2 LSTM模型
LSTM是一种变种的RNN,其精髓在于引入了细胞状态概念,不同于RNN只考虑最近的状态,LSTM为了能记住长期的状态,在RNN的基础上增加了一路输入和一路输出,增加的这一路就是细胞状态,LSTM的细胞状态会决定哪些状态应该被留下来,哪些状态应该被遗忘[5]。LSTM算法结构如图3所示。
算法如公式 ⑻ 至公式 ⑿ 所示。
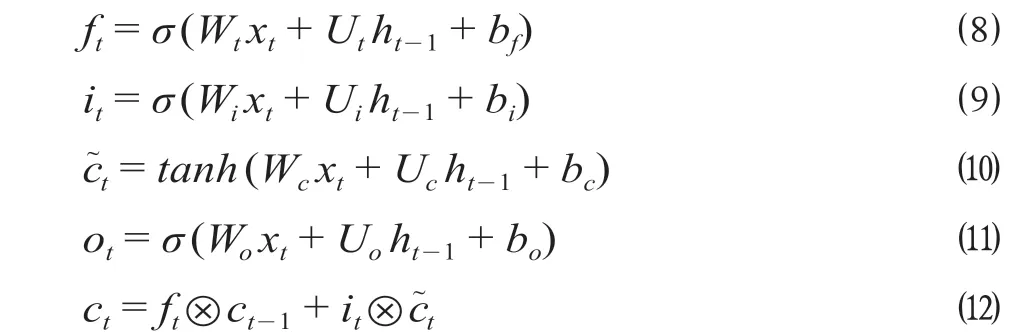
公式 ⑻ 中,ft是遗忘门,即一个遗忘值从0到1之间的数的向量,当遗忘值越接近于1时,与其相乘后的原先的细胞的信息会被更多的保留下来。相反,当遗忘值越接近于0时,与其相乘后的原先细胞的信息也会越接近于0,不被保留。公式⑿中,ft⊗ct-1代表上一时刻(t- 1)的细胞经过遗忘门后,被保留下来的信息量。
对于公式 ⑼ 中输入门it,同理也是一个元素值从0到1之间的数的向量。公式 ⑽代表当前时刻(t)需要更新到当前细胞状态的候选信息,之所以选择用tanh作为激活函数,是为了生成[-1,1]的值,迎合大多数场景下分布是0中心的需求。因此,公式 ⑿ 中代表当前时刻t真实加入到细胞状态里的当前细胞状态的候选信息量。
经过遗忘门的遗忘和输入门的输入后,最后当前细胞状态如公式 ⒀ 所示。

最后的输出门控制输出当前细胞状态的信息量的多少,即最后的输出信息量如公式 ⒁ 所示。

当输入的序列中,没有重要信息时,LSTM的遗忘门的值就接近于1,输入门的值接近于0,即过去的细胞记忆会被保存,从而实现长期记忆[6]。
1.3 GRU模型
GRU输入输出的结构与普通的RNN相似,其内部思想与LSTM相似。与LSTM相比,GRU内部少了一个“门控”,参数比LSTM少,但是却能够达到与LSTM相当的功能[7]。GRU模型结构如图4所示。
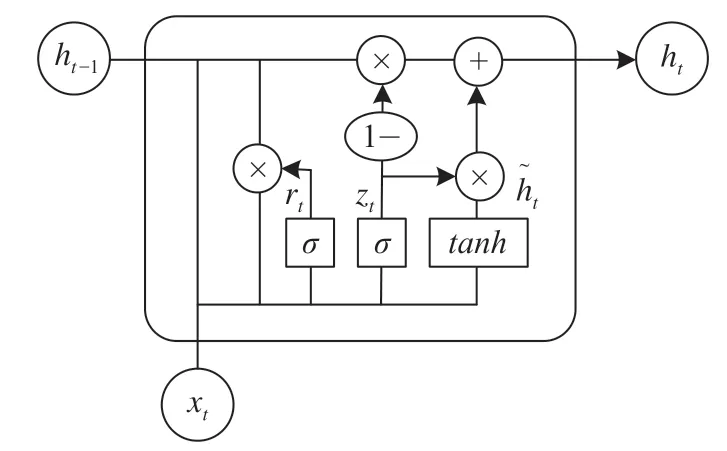
图 4 GRU模型结构Fig.4 GRU model structure
与LSTM相比,GRU把遗忘门和输入门结合为一个更新门zt,模型算法如公式 ⒂ 至公式 ⒅ 所示。细胞状态和隐藏单元都为ht,使得模型结构比LSTM更为简单。公式 ⒅ 中zt⊗代表当前时刻输入细胞状态的候选信息量,(1 -zt)⊗ht-1代表上一时刻被保留下来的信息量。若没有重要信息出现时,zt会接近于0,即细胞状态不会更新,ht会约等于ht-1,还是上一时刻的细胞状态[8]。
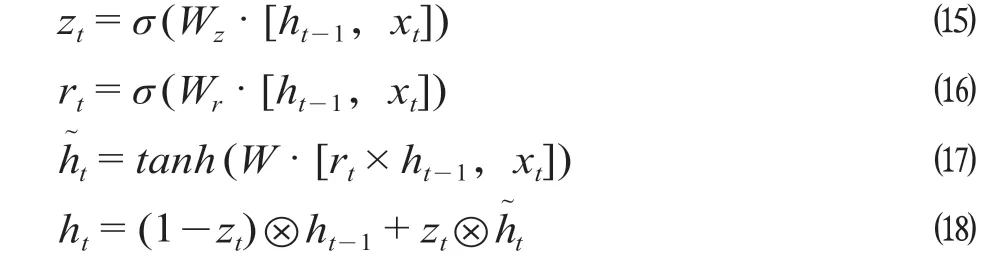
2 基于GRU模型的预测算法
基于GRU模型对客流预测的算法流程图如图5 所示,将原始客流数据进行预处理得到标准化数据,输入构造好的GRU模型进行训练,得到训练好的GRU模型,利用该模型得到最终的预测结果。
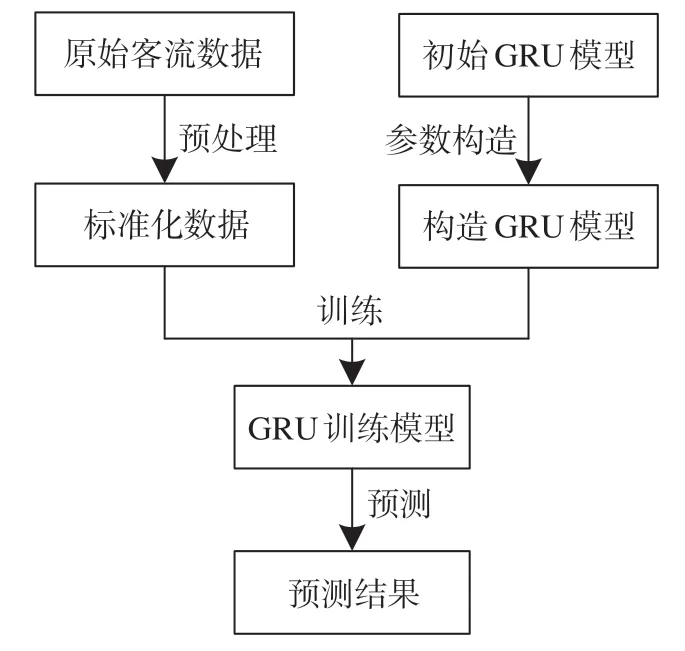
图 5 算法流程图Fig.5 Algorithm flow chart
2.1 数据预处理
数据来源为北京北站1年的进站客流数据,每30 min采集一次进站客流数,进站客流图如图6所示,展示了包含节假日在内的9月25日至10月4日 10天的数据,其中横坐标为时间,纵坐标为进站客流数。从波形可以看出其具有明显的周期特点,在早晨和傍晚呈高峰趋势,且在节假日时客流有明显提升。夜间车站关闭,客流量为0。
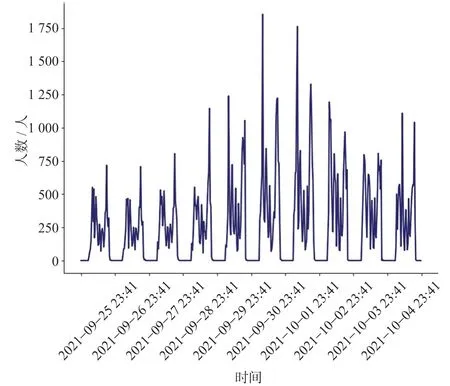
图 6 进站客流图Fig.6 Station passenger flow
以2021年9月30日当天的48个数据样本为例,1天内的客流数如表1所示。
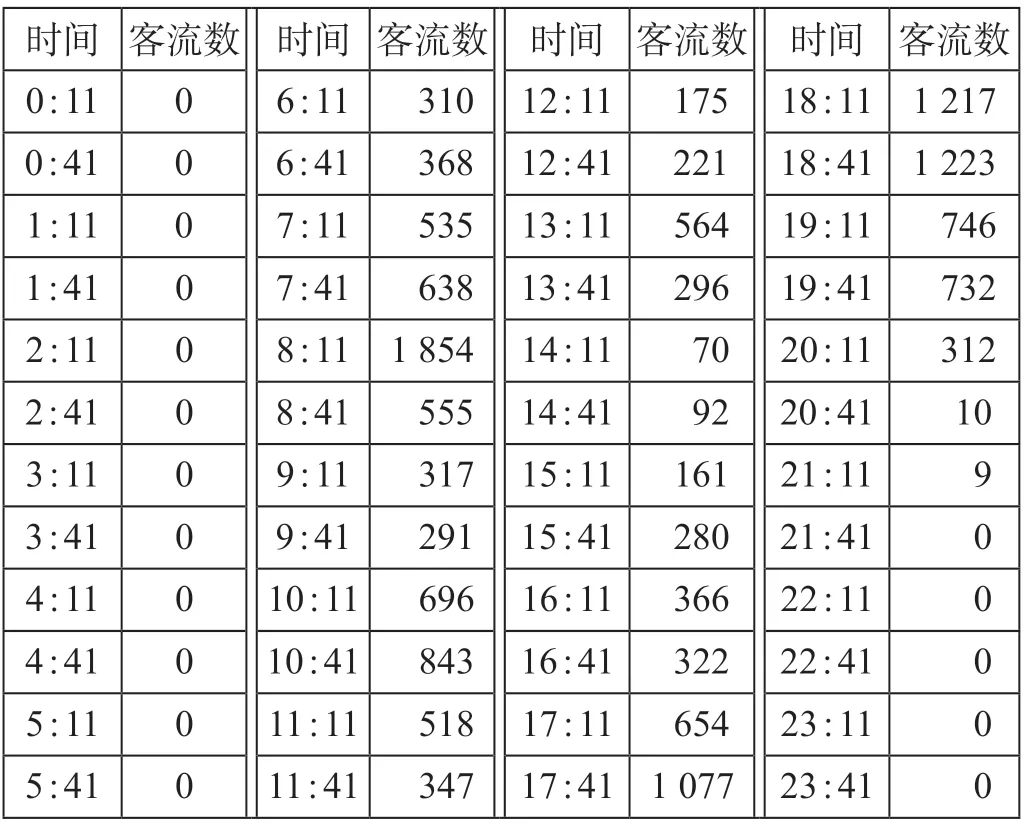
表 1 1天内的客流数 人Tab.1 Passenger flow within one day
对数据先做标准化处理,以减小所得结果误差。该数据值波峰波谷值差异较大,因此采用Z-Score标准化方法[9]进行处理。Z-Score能够将不同量级的数据转化为统一量度的Z-Score分值进行比较。首先计算总体数据均值、总体数据标准差,之后将观测值标准化,如公式 ⒆ 所示。

其中,x*为标准化后的样本值,x为个体观测值,μ为样本数据的均值,σ为样本数据的标准差。对每一天的数据单独做标准化处理,标准化样本如表2所示,保留2位小数。
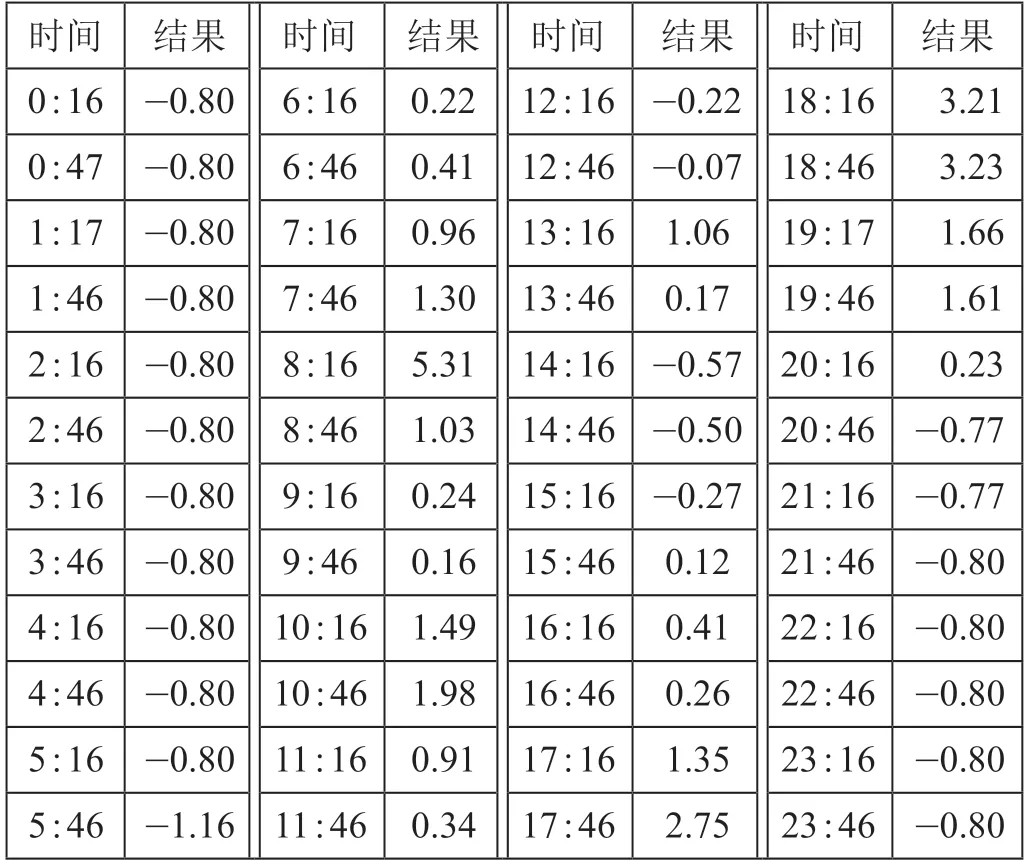
表 2 标准化样本Tab.2 Standardized sample
2.2 构造模型及训练
(1)构造GRU训练模型。首先将1年的原始数据导入,并按8 : 2的比例划分训练集X_train和测试集X_test,采用Z-Score标准化方法将数据进行标准化处理。
(2)构造GRU网络模型。GRU模型需要输入2个参数,一个是unit,一个是input_shape。形 式 为GRU (unit,input_shape = (TIME_STEPS,INPUT_SIZE))。unit指神经元的数量,input_shape指输入集的特征。TIME_STEPS代表序列本身的长度,INPUT_SIZE代表输入集的大小。根据数据集预测任务,unit取值为10,TIME_STEPS为48,INPUT_SIZE为1。另外,需指定GRU模型输出维度,格式为Dense (OUTPUT_SIZE),以及所采用的激活函数Activation,格式为Activation。由于输出维度为1,因此OUTPUT_SIZE取值为1,Activation采用softmax函数。
(3)GRU模型训练。将训练集输入构造好的GRU模型进行训练,迭代次数10 000次,批处理样本数为16[10]。
(4)预测。对最后1天(48条数据)的测试集进行预测,并与原测试集对比,计算出RMSE。
2.3 实验评价标准
评价标准采用均方根误差(RMSE)方法,该方法可以很好地反映算法的精度。RMSE是观测值与真实值偏差的平方和与观测次数比值的平方根。计算过程如公式 ⒇ 所示,yi为数据样本的真实值,为所计算的预测值,m为观测样本数[11]。
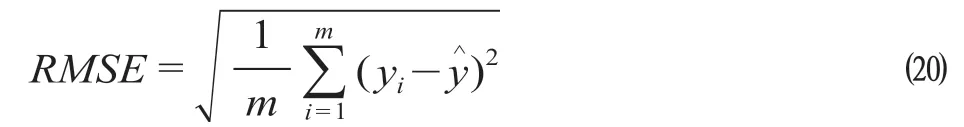
3 结果分析
用RNN,LSTM,GRU模型进行训练比对,迭代次数都为10 000次。RNN损失函数曲线如图7 所示,LSTM损失函数曲线如图8所示,GRU损失函数曲线如图9所示。3种循环神经网络的损失函数曲线在迭代8 000次左右趋于平稳趋势,收敛时间相当。最终的损失函数值RNN模型为0.82,LSTM模型为0.45,GRU模型为0.32。
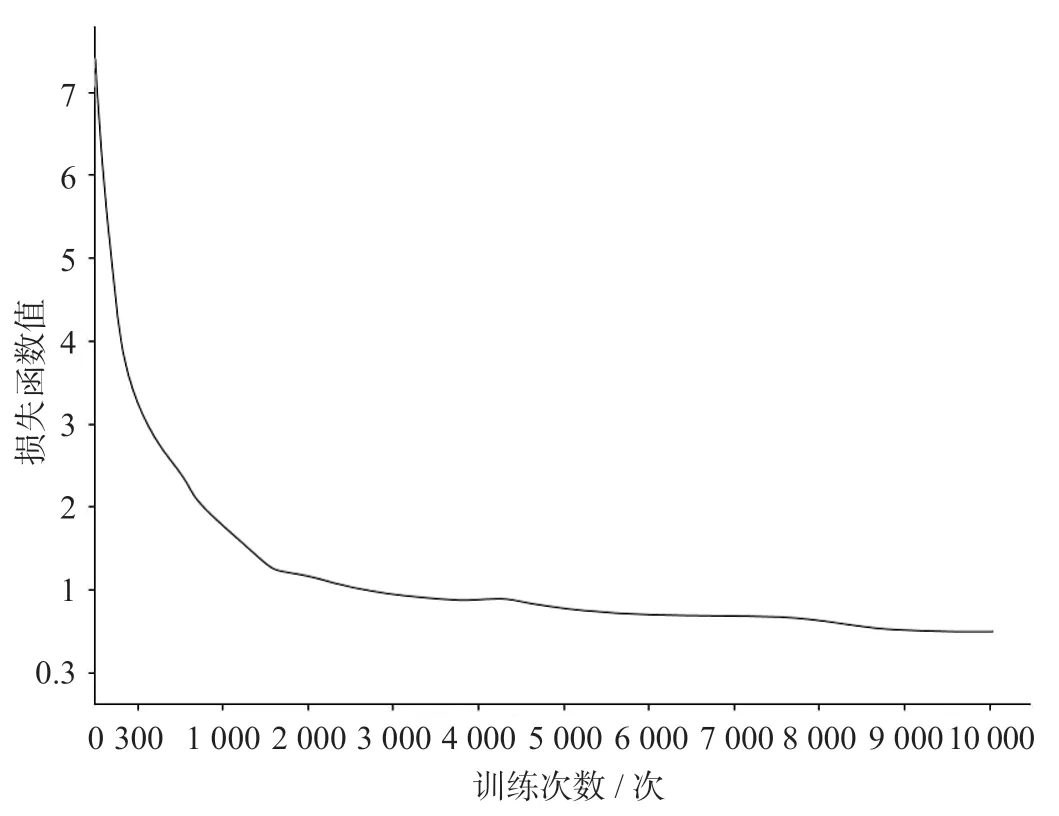
图 7 RNN损失函数曲线Fig.7 Loss function curve of RNN
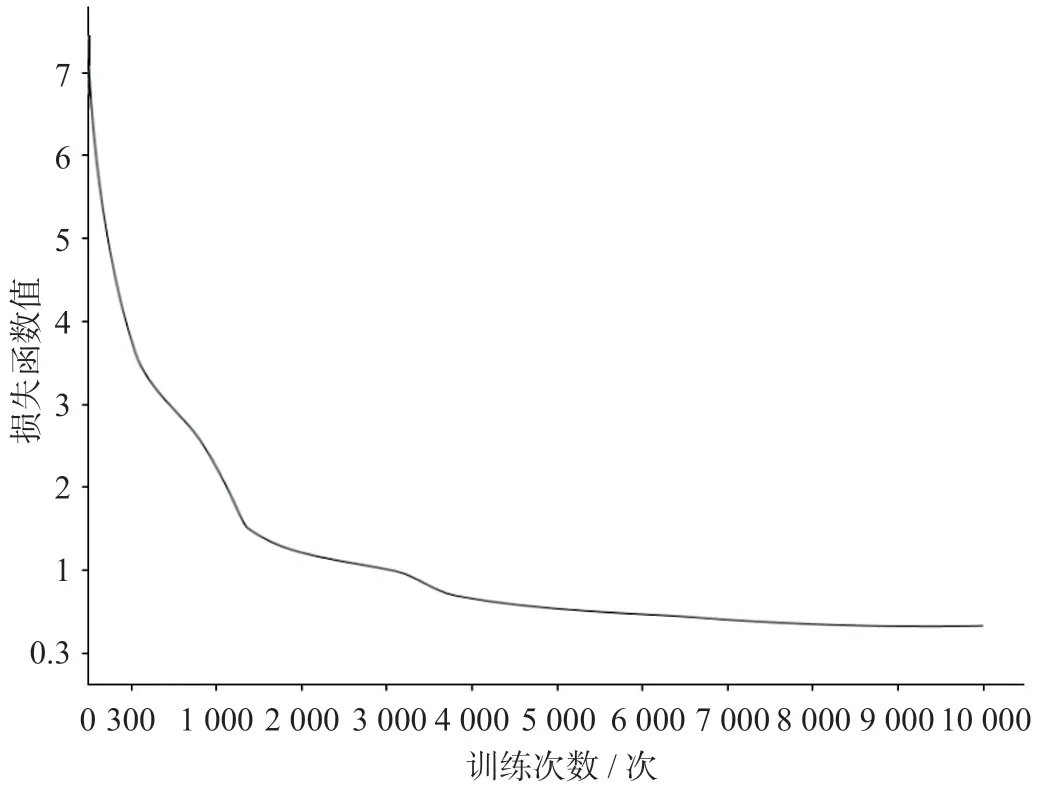
图 8 LSTM损失函数曲线Fig.8 Loss function curve of LSTM
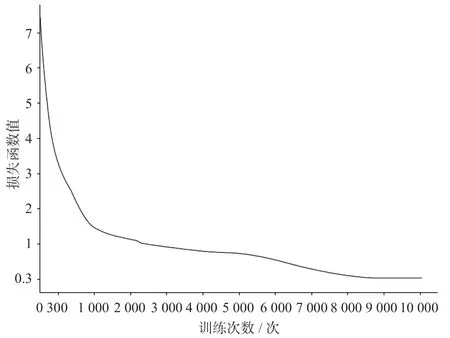
图 9 GRU损失函数曲线Fig.9 Loss function curve of GRU
采用GRU模型对客流量进行1天(48个时间点)的预测,GRU预测结果如图10所示。深蓝色波形代表原始样本观测值,红色虚线波形为GRU模型预测值。
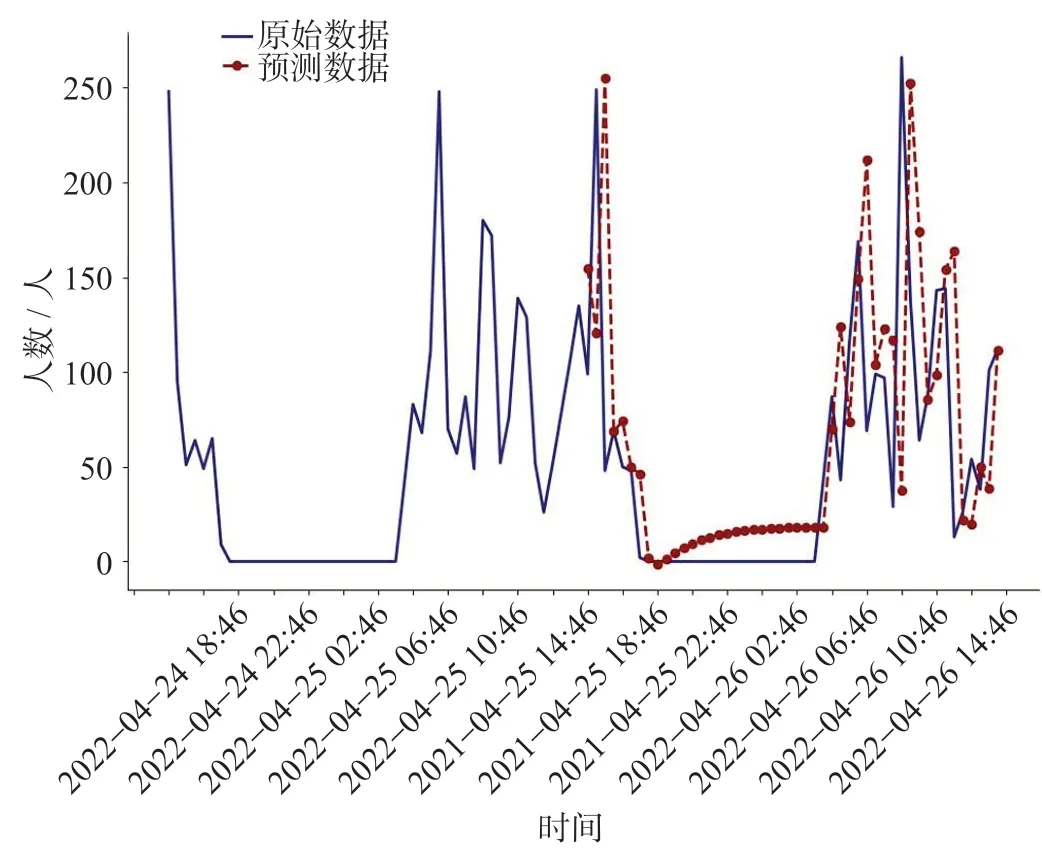
图10 GRU预测结果Fig.10 Predicted results of GRU
采用RNN,LSTM对客流量进行预测对比,RNN预测结果如图11所示,LSTM预测结果如图12 所示。与图10对比可以看出,采用GRU模型的预测结果对凸起的波峰有更高的灵敏度,也更接近原始波形。
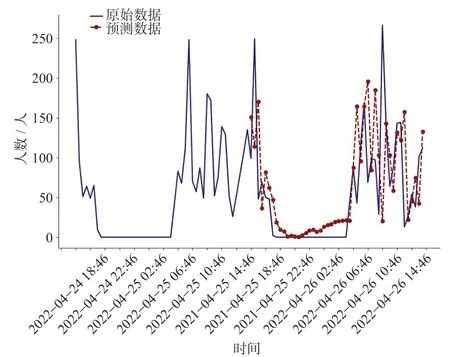
图 11 RNN预测结果Fig.11 Predicted results of RNN
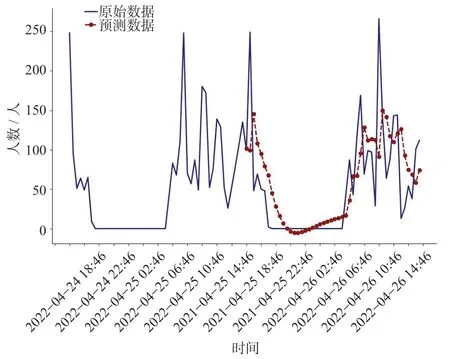
图 12 LSTM预测结果Fig.12 Predicted results of LSTM
3种模型的RMSE结果比对如表3所示。GRU的RMSE最低,误差最小。

表 3 RMSE结果比对Tab.3 RMSE result comparison
4 结束语
通过分析客运站往年实际发送客流量,提出了使用GRU模型对客流量进行预测的方法。以北京北站1年的客运发送量为样本,分析其客流特征后采用Z-Score方法进行标准化处理。利用GRU模型按照划分的训练集和测试集进行训练,构造GRU模型。按照该模型对北京北站客流量1天的客流进行预测,并且与RNN模型、LSTM模型进行了对比测试。通过RMSE比对与波形分析,GRU的RMSE更低,且更接近原始波形。利用GRU模型算法对客运站发送量进行预测,可使客运人员提前预知下一时刻的进站客流数据,对车站及时疏散旅客、防范风险具有重要意义。
