基于参考点相依效用的区间Orthopair多属性决策方法
2022-09-26周礼刚林志超
许 颖,徐 鑫,周礼刚,3,林志超
(1.安徽大学 文典学院,安徽 合肥 230601;2.安徽大学 数学科学学院,安徽 合肥 230601;3.安徽大学 应用数学中心,安徽 合肥 230601)
多属性决策问题是决策科学的重要组成部分,其理论和方法在经济、管理等很多领域有着非常广泛的应用。由于研究对象的不确定性,很多情况下无法对研究对象的属性用一个精确的值加以描述,美国加州大学ZADEH教授于1965年创立的模糊集理论[1]应运而生。学者们进行了深入的研究,ATANASSOV[2]同时考虑了隶属度,非隶属度,犹豫度3个方面,提出直觉模糊集,在处理不确定性时更具灵活性和实用性。YAGER等[3-4]提出毕达哥拉斯模糊集,其隶属度与非隶属度的平方和不能大于1。在毕达哥拉斯模糊集的基础上,又提出了q-rung Orthopair模糊集,满足隶属度与非隶属度的q次方和不能大于1[5]。考虑到在实际决策过程中,客观信息的不足使得属性值很难用一个精确的数进行表示,WANG等[6]定义了区间值Orthopair模糊集,其中隶属度和非隶属度都是[0,1]的区间数,以便更加细致地度量模糊信息。q阶区间Orthopair模糊集是将q-rung Orthopair模糊集的隶属度与非隶属拓展到区间范围,已经有众多学者对此开展研究。黄荣等[7]研究了基于区间q-rung Orthopair模糊相似测度的模糊识别方法。汪烨等[8]提出基于区间q-rung Orthopair模糊Minkowski距离测度的TOPSIS决策方法。陈艳如等[9]研究了基于区间Orthopair模糊Heronian测度的多属性群决策方法。
根据前景理论可知,决策者在进行风险投资时,具有主观的风险偏好[10-11]。考虑该因素,更能反映决策者的实际选择过程。目前基于前景理论的决策问题已经被广泛运用于诸多方面,但仍未有与q阶区间Orthopair模糊集相结合的研究或多属性决策方法。因此提出一种运用前景理论中参考点相依效用函数在q阶区间Orthopair模糊集中进行多属性决策的方法。首先,在新的记分函数环境下,疫苗方案各属性的q阶区间Orthopair模糊数更容易计算和比较。其次,根据参考点相依效用函数,得到疫苗各方案的参考点相依效用矩阵。最后,建立疫苗属性的权重优化模型,求出权重并得到各疫苗方案的综合评分值,以供决策者进行选择和投资。
1 预备知识
定义1设X为一论域,称I={
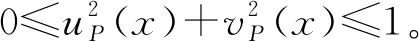
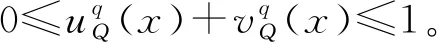
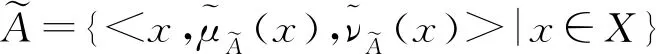
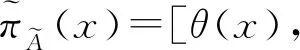
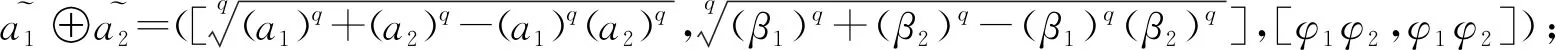
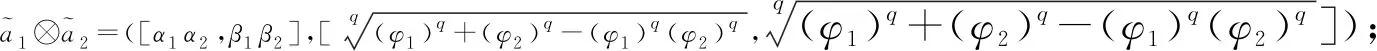
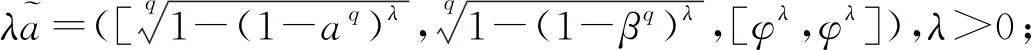
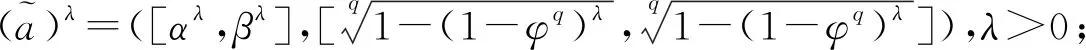
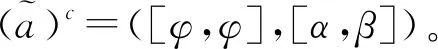
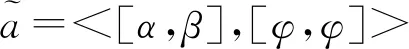
(1)
(2)
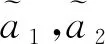

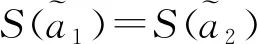
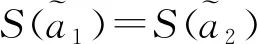
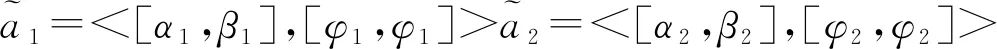
(3)
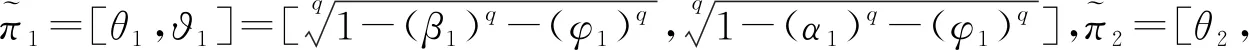
前景理论指出,决策者在收益面前具有风险规避态度,在损失面前具有风险偏好态度的“有限理性”行为[10-11]。前景价值由价值函数和概率权重函数决定,其中前景价值函数是决策者根据实际收益或损失产生的主观感受价值。TVERSKY等[11]提出前景价值函数为典型的参考点相依效用函数,如式(4)所示。
(4)
式中:u(x)为前景价值函数;b为参考点,当x大于b时,视为收益,当x小于b时,视为损失;θ为损失规避系数,决策者对于损失的敏感程度与θ成正比,θ越大,决策者的敏感程度越大,若θ>1,则说明决策者对损失的敏感程度比对收益的敏感程度大;Α,Β为风险态度系数(0<Α,Β<1),反应决策者对收益和损失的敏感程度。经验数据认为Α=Β=0.88,θ=2.55。
根据前景价值函数和幂函数的凸凹性,收益时u(x)为凹函数,说明决策者面对收益表现出风险规避态度;损失时u(x)为凸函数,此时决策者面对损失表现出风险偏好态度。 S型参考点相依效用函数的一般形式如式(5)所示。
(5)
式中:b为参考点。决策者面对收益时,价值函数为凹函数;面对损失时,价值函数为凸函数。价值函数为单调递增函数。
非S型参考点效用函数的一般形式如式(6)所示[14]。
(6)
式中:θ为损失厌恶系数。若v1(x)=x,θ=0,则说明决策者是风险中立的。
2 一种新的q阶区间Orthopair模糊集记分函数
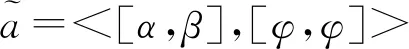
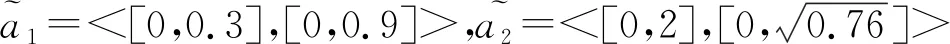
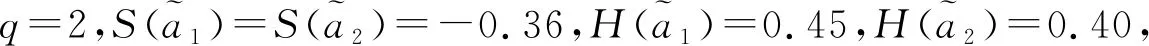
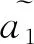
可见当隶属度只有0.001的变化时,用得分函数和精度函数比较大小,得到的却是完全相反的排序结果。说明在比较的过程中,仅仅考虑隶属度和非隶属度而忽略犹豫度,会丢掉一些有用的信息,使得结果存在偏差。同时,该运算没有考虑不同q-RIVOFN隶属度和非隶属度之间存在的关联和相互影响。因此,需要在q阶区间Orthopair模糊集中引入新的记分函数,同时考虑隶属度、非隶属度和犹豫度,并且考虑隶属度和非隶属度之间存在着的关联和相互影响,使之具有较强的选择能力和较高的精确度。基于上述研究,提出q-RIVOFN的隶属度区间中值、非隶属度区间中值和犹豫度区间中值等概念。
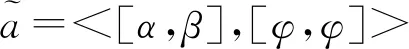
(7)
(8)
(9)
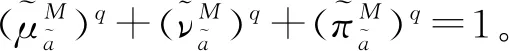
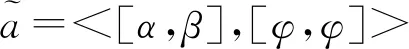
(10)
(11)
(12)
决策者在进行决策时,总是认为更优方案具有高隶属度、低非隶属度和犹豫度。将决策者的从众心理推广到q-RIVOFN中,则可以用q-RIVOFN的交叉熵将犹豫度细化为倾向支持、反对和中立。基于上述原理,提出改进的记分函数。
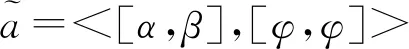
(13)
(14)
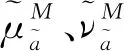
新记分函数避免了在得分函数、精度函数下大小比较存在偏差的情况。同时,考虑了隶属度、非隶属度和犹豫度以隶属度与非隶属度的关系,使得包含的信息量更全面,有利于比较大小。
3 基于参考点相依效用函数的q阶区间Orthopair模糊多属性决策方法
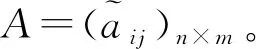
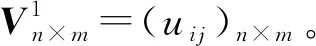
(15)
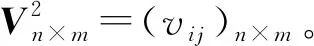
(16)
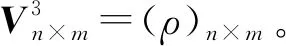
ρ(sij)=sij
(17)
(18)
(7)建立参考点相依效用函数的q阶区间Orthopair模糊多属性决策问题的权重优化模型。以各个方案的各个属性对于其重要性一致为原则,取使各个属性的属性值差异最小的权系数。此外,针对属性值的分布情况,认为在同一属性下,各方案属性值差异越大,则认为该属性是有利于方案的排序和选择的,并赋予它较大的权系数;反之,属性值差异越小,则赋予该属性较小的权系数。设wki为第k种投资者态度下属性Pi的权重;O为权重取值范围;r1,r2分别为属性权重公平性和属性值分布情况对于权重取值的相对重要性。权重的优化模型如式(19)所示。
(19)
借助Python软件进行求解,可以得到最优属性权重wk*={wk1,wk2,…,wkn}T,k=1,2,3。
4 实例分析
4.1 实例
疫苗企业具有周期长,风险大,收益高的特点[15-18],故投资疫苗企业也风险和收益并存。疫苗的研发时间较长,具有研发和接种的双重风险,高收益就成为疫苗企业的风险补偿。目前共有5个疫苗方案供投资者考虑,记作M1,M2,M3,M4,M5。考虑如下6个属性:疫苗对应疾病的危险性P1、疫苗的安全性P2、疫苗的有效性P3、疫苗可能的不良反应P4、疫苗的研发价格P5、疫苗的研发时间P6。现有3个专家对此进行评估,专家对于相对收益或损失的态度各不相同:①第一位专家对相对收益持有风险规避态度,对相对亏损持有风险偏好态度;②第二位专家对相对收益和相对亏损均持有风险规避态度;③第三位专家对相对收益和相对亏损持有风险中立态度。经过专家评价商议,对5个候选方案的6个属性进行评估,进行统计处理后,可得专家评议决策表格,如表1所示。
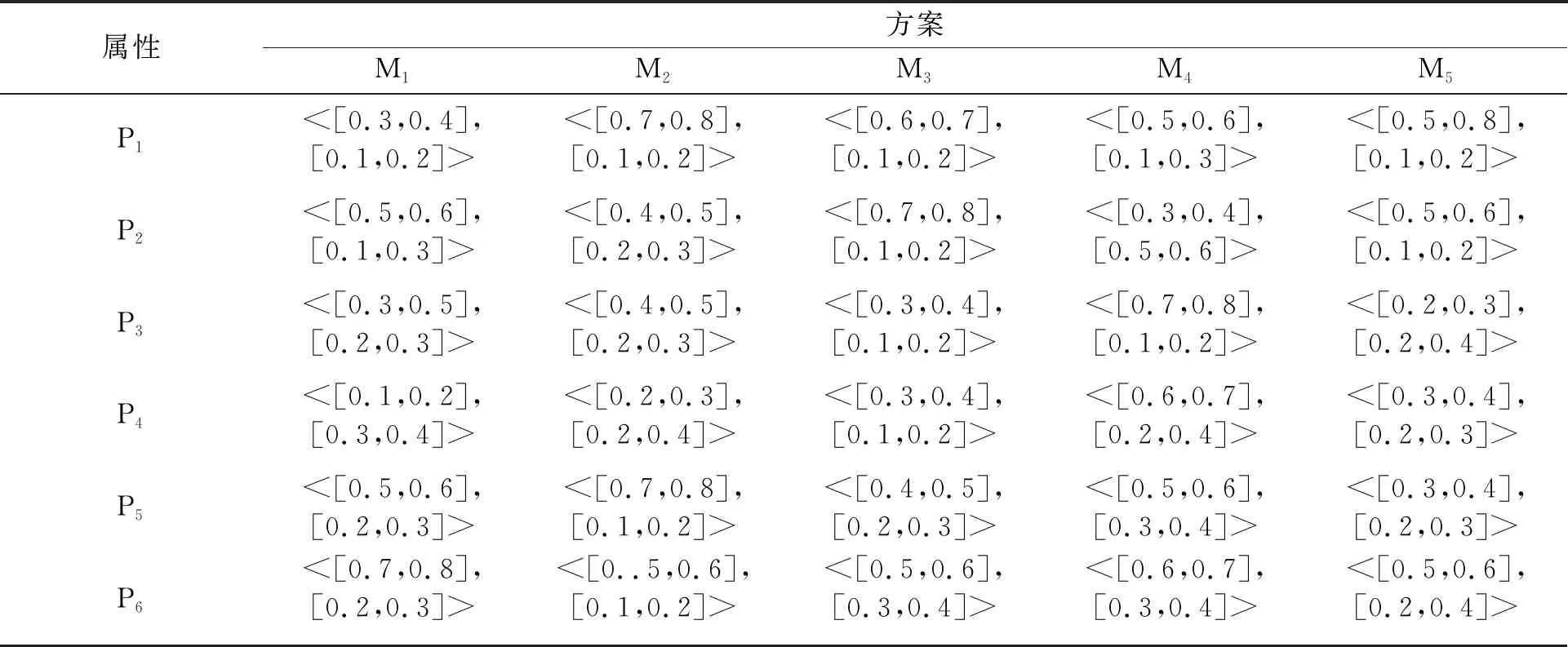
表1 专家评议决策表
取q=1,由式(13),可得记分函数值矩阵:
S6×5=
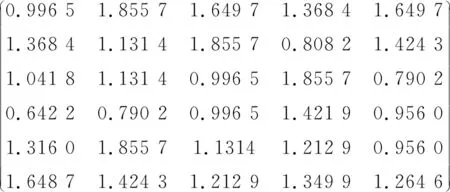
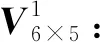
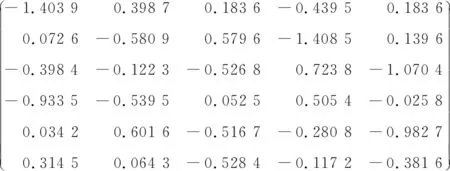
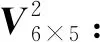
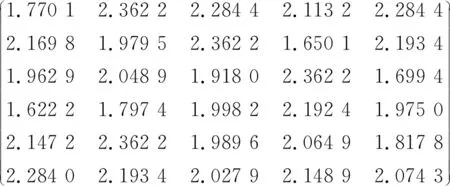
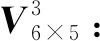
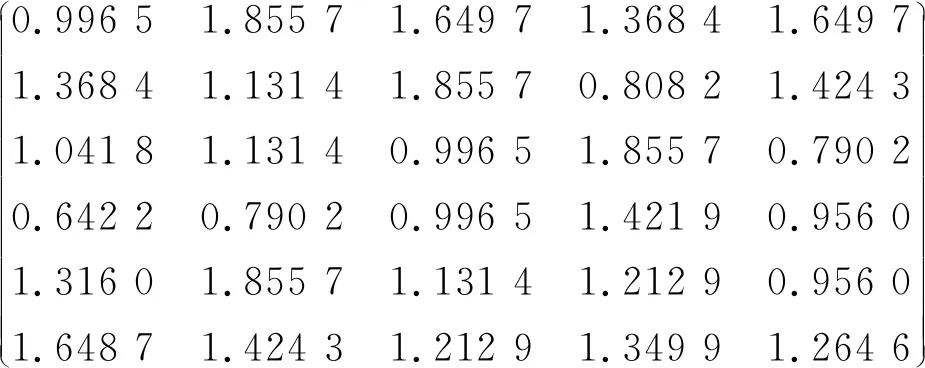
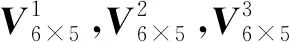
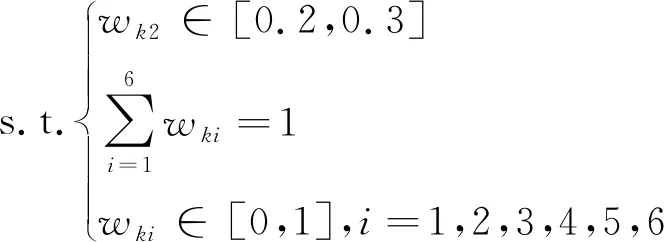
可得3种决策者态度下的各属性值的权重系数,分别为w1*={0.70,0.20,0,0,0,0.10}T,w2*={0.79,0.20,0,0,0,0.01}T,w3*={0.34,0.20,0,0.01,0.02,0.43}T。
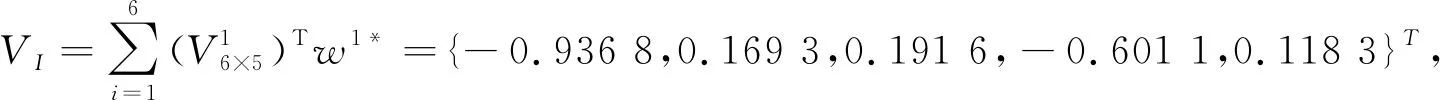
4.2 灵敏度分析
为考察不同q值对决策结果的影响,进行灵敏度分析。取q=2,…,8,依次重复上述决策过程,结果如图1所示。由图1(a)可知,当决策者对相对收益持有风险规避态度,对相对亏损持有风险偏好态度时,q=2,…,7时,最优方案均为M1,但M1的综合效用值始终呈下降趋势;当q=8时,M1不再是最优方案。由图1(b)可知,当决策者对相对收益和相对亏损均持有风险规避态度时,q=2,…,6时,最优方案均为M1,但各方案的综合效用值均呈下降趋势;当q=7时,M1不再是最优方案,M4变为最优方案。由图1(c)可知,当决策者对相对收益和相对亏损持有风险中立态度时,各方案的综合效用值均呈下降趋势,从q=3时,M4一直为最优方案。
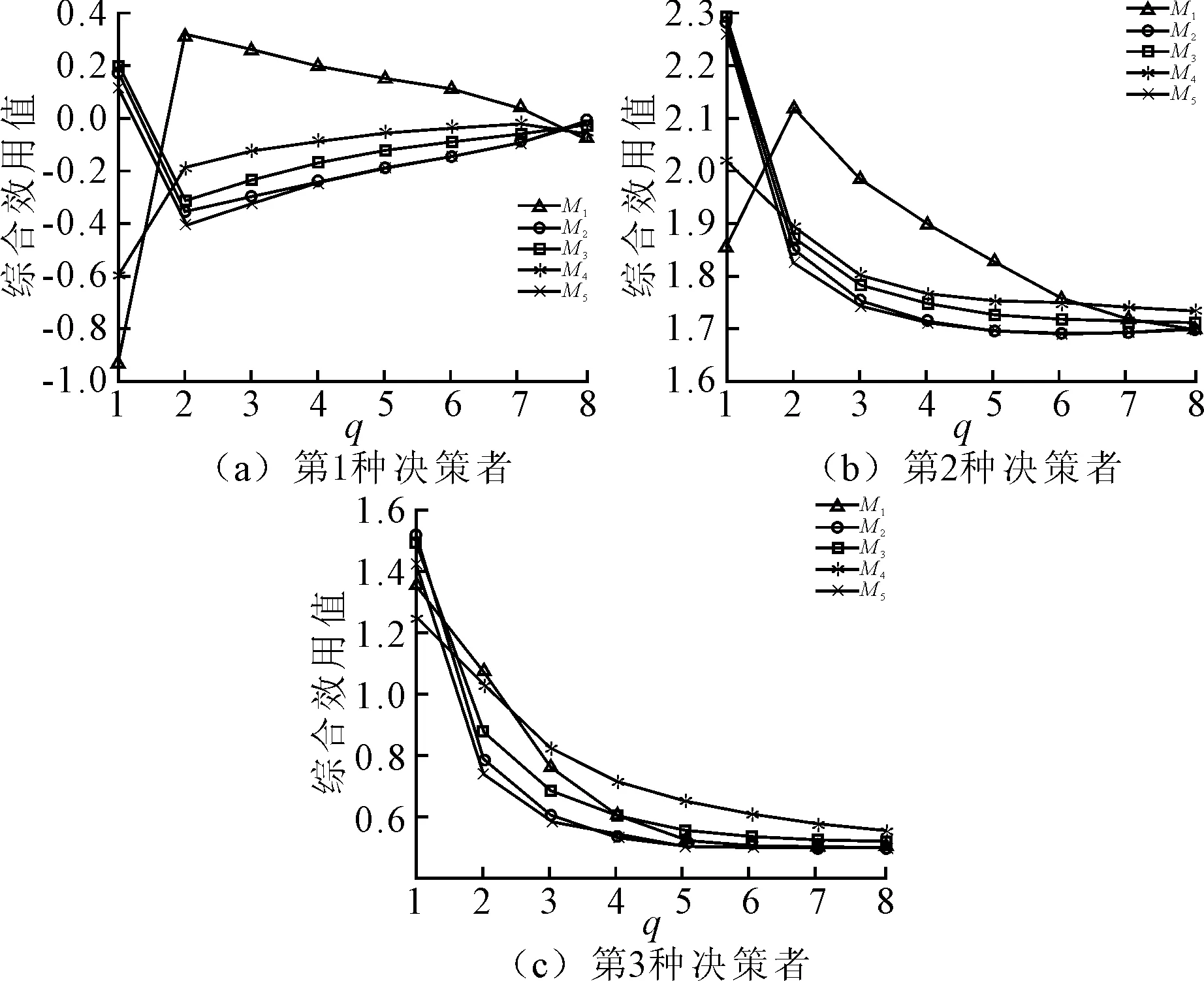
图1 3种决策者态度下不同q值方案的综合效用值变化
为考察不同的r1,r2(1+r2=1)对决策结果的影响,分别取q=1时,r1=0.3,r1=0.4,r1=0.5,r1=0.6,r1=0.7,重复上述决策步骤,结果如图2所示。由图2(a)可知,当决策者对相对收益持有风险规避态度,对相对亏损持有风险偏好态度时,最优方案均为M3。由图2(b)可知,当决策者对相对收益和相对亏损均持有风险规避态度时,随r1变化,最优方案始终为M3。由图2(c)可知,当决策者对相对收益和相对亏损持有风险中立态度时,从r1=0.35时,M2始终为最优方案。
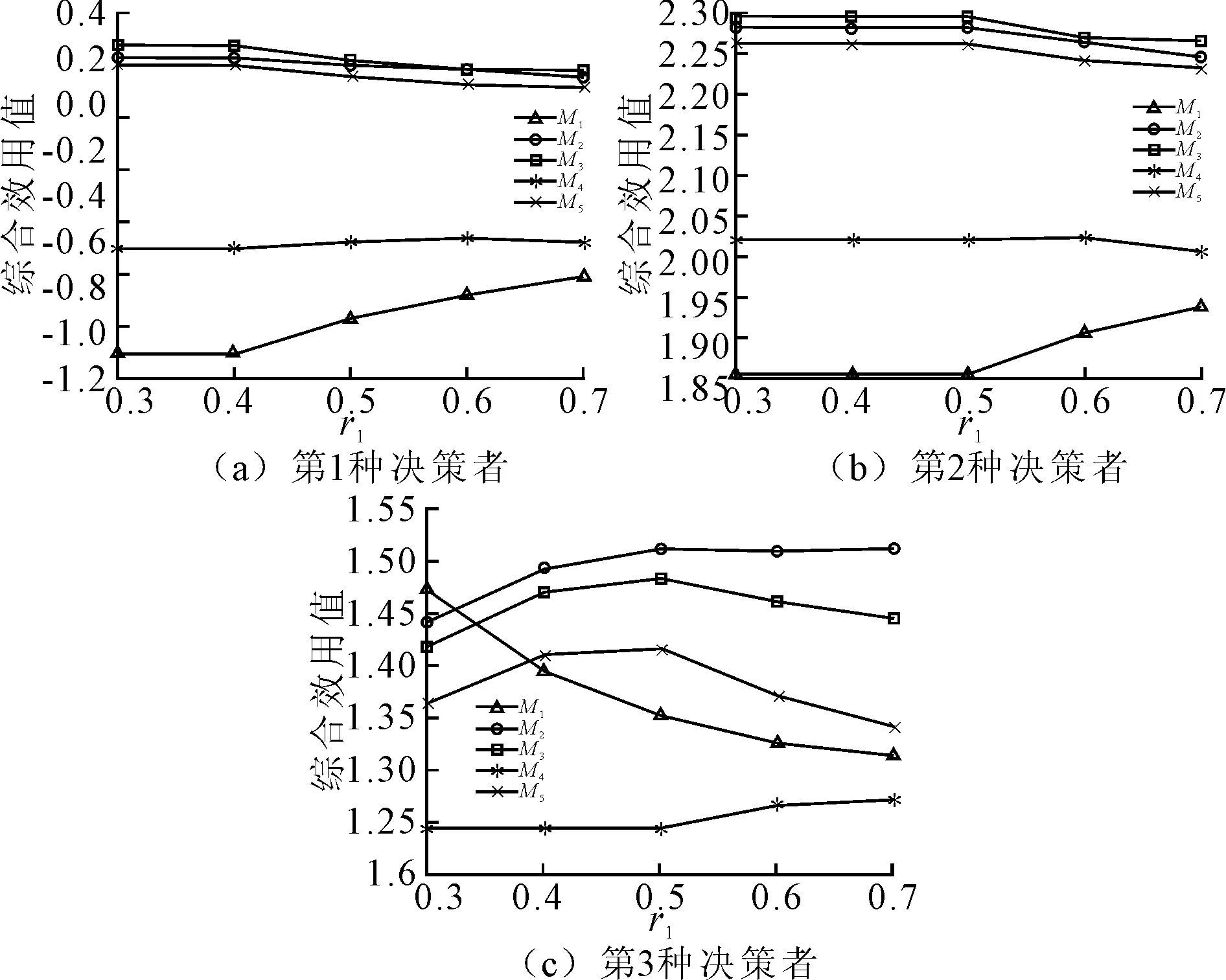
图2 3种决策者态度下不同r1方案的综合效用值变化
4.3 对比分析
在实际的决策中,相较于q阶Orthopair模糊集属性值的数值表示方式,q阶区间Orthopair模糊集的属性值可以用区间数进行表示,能更加细致地度量模糊信息,在客观信息不足时,具有更强的实用性和准确度。
与q阶区间Orthopair模糊集的其他记分函数进行对比,提出的新的记分函数具有明显优势。下面用文献[12]中的得分函数在q=3,决策者对相对收益持有风险规避态度,对相对亏损持有风险偏好态度下为例,可得各方案的综合效用值为{-0.061 6,-0.065 7,-0.070 6,-0.229 9,-0.099 4}T,方案排序为M1≻M2≻M3≻M5≻M4,最优方案为M1,与新记分函数结果一致,说明提出的新记分函数是可行的。同时,提出的新记分函数能将隶属度、非隶属度和犹豫度以及隶属度与非隶属度关系考虑进去,包含的信息更为全面,更有利于进行大小的比较。而文献[12]中的记分函数并未考虑犹豫度以及隶属度与非隶属度之间的关系,在一些情况下会出现无法进行比较、或者比较结果不稳定性的现象。故提出的新记分函数可以增加决策结果的准确性。
与q阶区间Orthopair模糊集的其他多属性决策方法进行对比,如文献[8]和文献[9],创新之处在于算子的改变,不同的算子采用了不同的集结方法,而并未对决策者的现实心理进行考虑。综合考虑决策者主观的风险偏好,引入参考点相依效用函数,提出的基于参考点相依效用函数的多属性决策方法更符合决策的现实情况,具有现实意义。
提出的运用前景理论中参考点相依效用函数在q阶区间Orthopair模糊集中进行多属性决策的方法相较于文献[19],是对已有区间直觉模糊运用参考点相依效用函数进行多属性决策的一种推广。决策者可以根据具体的情况选定合适的参数q,因此具有更好的普适性。
5 结论
在区间Orthopair模糊环境下,提出一种运用前景理论中参考点相依效用函数在q阶区间Orthopair模糊集中进行多属性决策的方法。该方法不仅综合考虑了隶属度,非隶属度和犹豫度以及隶属度与非隶属度的关系,还更有利于计算;根据前景效应中参考点相依效用函数,将决策者的“有限理性”考虑进去,更符合实际情况;结合参考点相依效用矩阵,利用权重优化模型计算权重,得到各方案的综合评分值进行排序,以供决策者进行选择和投资。
该方法是对q阶区间Orthopair模糊决策理论的有益扩展,可用于药物疗效评估、投资选择、模式识别、重大工程选址等诸多不确定环境决策领域。
