基于自适应S曲线算法的巡检机器人速度规划
2022-09-26傅国辉丛峰武李熙然刘皓月
傅国辉 丛峰武 李熙然 刘皓月
1.鞍山钢铁集团有限公司齐大山选矿厂;2.大连交通大学
针对巡检机器人在运行过程中速度变化过快会导致运动控制系统稳定性差的问题,采用S形加减速曲线算法对机器人进行速度规划,减小其在起步和制动阶段的震荡,使其能够在轨道上的平稳运行。本文在传统S曲线基础上提出了自适应S曲线算法,在算法中加入约束公式,根据是否满足等式关系来判断S曲线加减速曲线状态,可以自动调整数值,仿真结果表明,改善后的S曲线算法在速度控制中有较好的效果。
随着智慧矿山的兴起,越来越多的现代化设备在煤矿上投入使用,在煤矿运输的多个环节都有着带式输送机的身影,带式输送机具有布线灵活、可连续输送、能耗低等特点,但是在运输过程中,机头振动发热、传送带磨损卡带、托辊发热等部件出现故障,给生产带来严重的安全隐患。此时就急需无人值守的智能巡检机器人来进行智能巡检[1]。
在巡检机器人智能巡检的过程中,如果没有合适的控制算法,在机器人运行的过程中会产生一定程度的噪声或者抖动,并且定位误差也比较大。平滑、稳定的运动能够降低对机械部件的磨损,使运动过程更加连贯。因此选择合适加减速控制算法,保证机器人运行平稳。目前比较常用的机器人加减速控制算法主要有梯形、指数形和S形。本文在传统7段式S曲线算法的基础上,提出了一种自适应S曲线算法,实时调整S曲线的状态。
1 加减速控制算法
加减速控制算法是实现巡检机器人运动控制系统高实时性的重要组成部分,一个好的加减速控制算法可以保证巡检机器人在巡检过程中运行平稳,减少机器人在启动时速度突变对电机的冲击和机械磨损,并能够优化巡检机器人的运行轨迹和实时响应速度,提高系统的工作效率和精度。常用的加减速算法包括:梯形加减速、指数形加减速和S形加减速。
1.1 梯形加减速控制算法
在速度规划算法中,梯形加减速控制算法,系统加减速时间短。梯形加减速控制可分为加速阶段、匀速阶段、减速阶段。加速阶段与减速阶段的加速度大小相等,方向相反。在起始处以恒定不变的加速度一直加速到最大速度Vmax,然后保持匀速运行,最后以恒定的加速度减速到最终速度Vend[2],其速度和加速度原理曲线原理如图1所示。
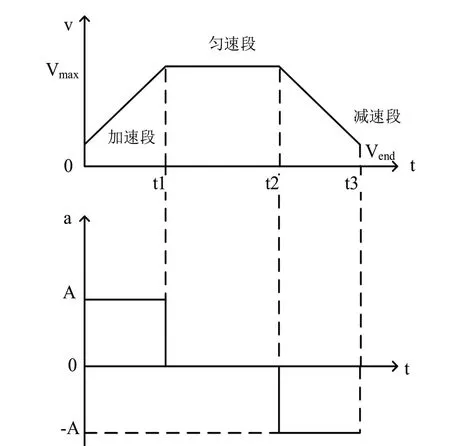
图1 梯形曲线原理图Fig.1 Principle diagram of trapezoidal curve
1.2 指数型加减速控制算法
指数曲线加减速算法具有较强的跟踪性,起点和终点存在加速度突变,高速时稳定性弱,与梯形加减速法相比,指数形平滑性好,运动精度高,但在加减速的起点仍然存在加减速突变,因此也不用于需平稳运行的轨道式巡检机器人控制系统。指数形加减速曲线的速度和加速度轨迹如图2所示。
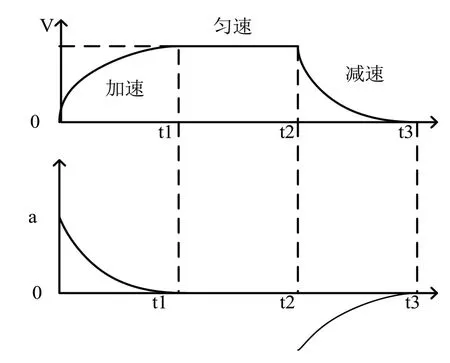
图2 指数形曲线原理图Fig.2 Schematic diagram of the exponential curves
1.3 S形加减速控制算法
S形曲线是目前较新的运动控制算法,它是由被控对象的加减速阶段的速度曲线呈S形而得来。常见的S曲线有抛物线型和三角函数型。S曲线算法的核心思想是让加速度不产生突变,从而使被控对象的速度控制具有快速、平稳的特性。本研究将以抛物线为例来对S曲线进行分析[3]。完整的S曲线包括以下几个阶段:加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段和减减速段,通常情况下S曲线需要三个基本参数:最大速度Vmax,最大加速度amax,加加速度J,如图3所示。
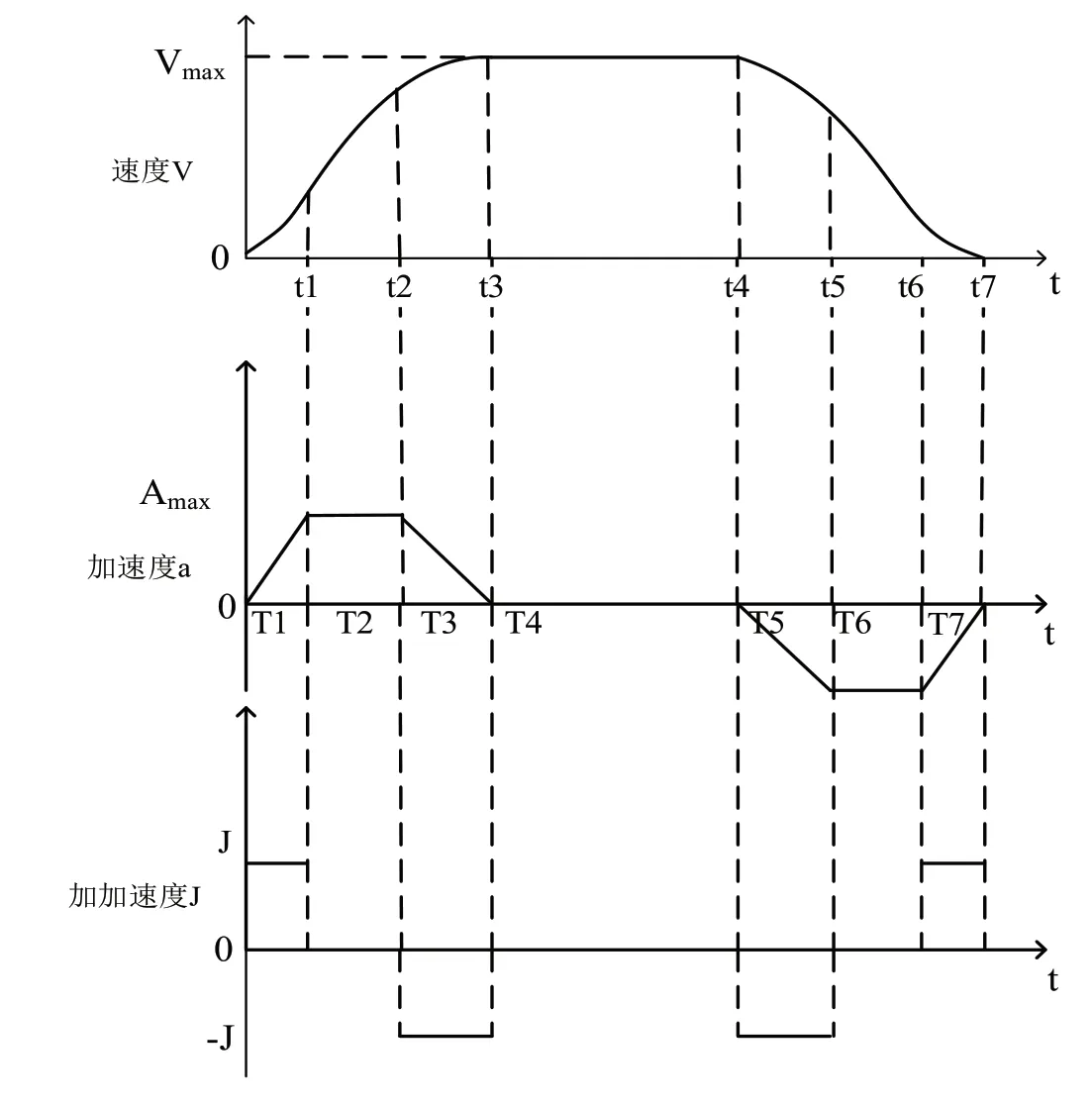
图3 S曲线原理图Fig.3 Schematic diagram of S curve
加速度时间关系方程如下所示:

速度时间关系方程:
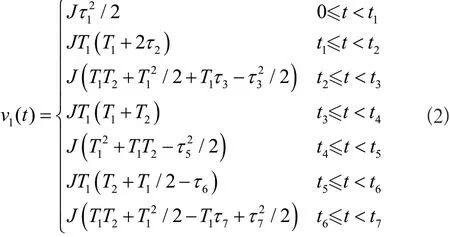
位移时间关系方程:
2 梯形、指数形和S形曲线之间的联系
梯形、指数形和S形曲线都是在被控对象的加减速阶段对其进行速度规划,从而使其能够快速、平稳地达到运动系统的动作要求。假设用t1表示被控对象变加速阶段的时间,用t2表示被控对象匀加速阶段的时间。当t1≠0,t2=0时S形曲线就变成了三角形曲线(如图4所示),此时被控对象加减速时间最长;当t1=0,t2≠0时S形曲线就变成了梯形曲线(如图5所示),此时被控对象加减速时间最短,但加速度有突变;当t1≠0,t2≠0时S形曲线算法实现也较为复杂(如图6所示),但是在快速启动、失步和平稳性上均有较好的性能。此时t1和t2的选取就需要根据被控对象的性能进行灵活选取[4]。
图4 三角形曲线Fig.4 Triangular curve
图5 梯形曲线Fig.5 Trapezoidal curve
图6 S形曲线Fig.6 S-shaped curve
在本系统中,设巡检机器人的最大速度为1m/s,最大加速度为50cm/s,最大加加速度为20cm/s,在同等条件下利用仿真软件对三种加减速控制算法进行仿真,如图7所示。
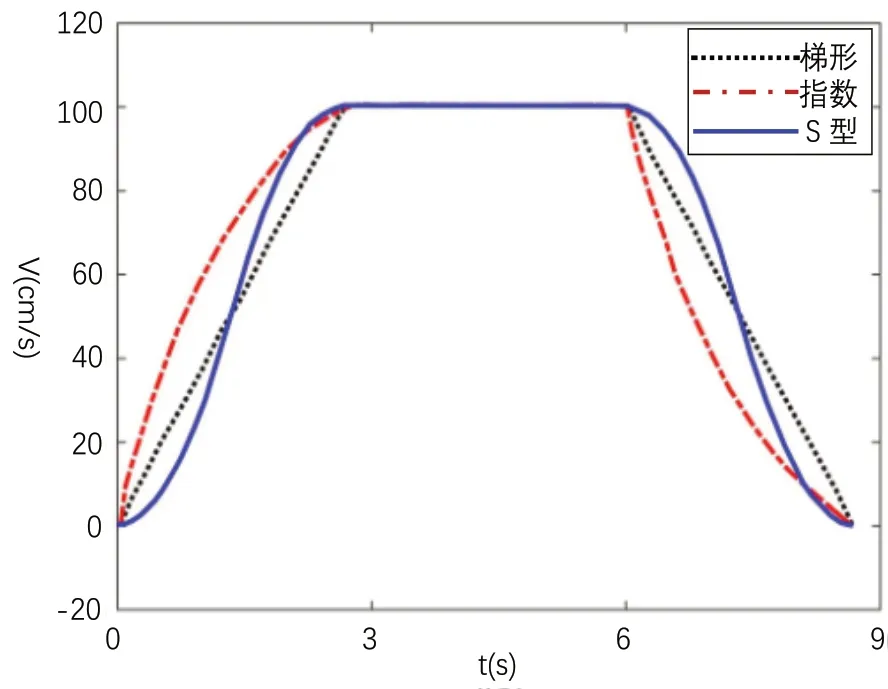
图7 三种加减速算法仿真图Fig.7 Simulation diagram of three acceleration and deceleration algorithms
由图7可知:S形加减速和指数型加减速的速度变化都较为平滑;在减速阶段,指数形加减速和直线加减速的速度都存在突变。由以上分析可得,S形加减速在整个速度调节过程中都十分平滑,不存在突变,因此巡检机器人运动控制系统可用S形加减速运动控制算法对加减速进行调节[5]。
3 改进自适应S曲线算法
S曲线规划需要确定三个最基本的系统参数:最大速度Vmax,最大加速度amax,加加速度J,在实际应用中,由于被控对象约束条件的不一样,运动的过程就会发生相应的变化,S曲线会有不同情况。在运行过程中只有达到最大速度的时候才可以形成一个完整的7段S曲线,在这个过程中还存在一些中间参数[6]:
假设存在T2和T6
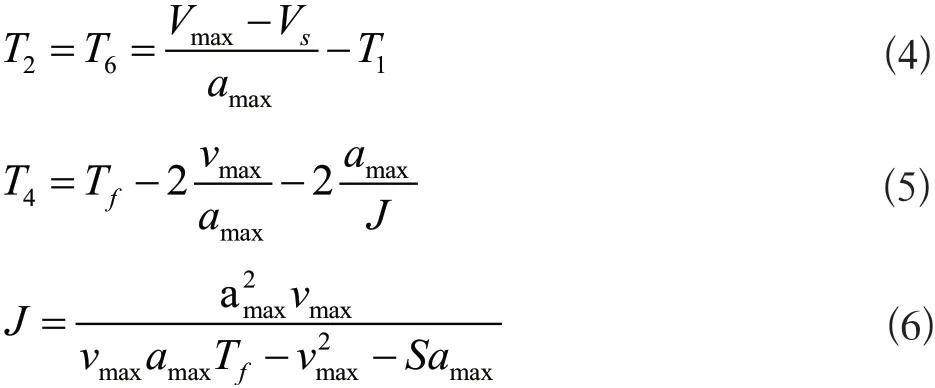
式中:Tf为运行总路程,S为总位移,J为加加速度。
在运行过程中,当T2和T6大于0时候就是完整的七段式S曲线;当T2和T6小于0时就是五段式S曲线;当T4也小于0就是4段式S曲线。
自适应约束公式如下:

在仿真软件中假设初始速度默认为0,终止速度也为0,并且假设加减速区域相互对称。设置ThetaStart=0;ThetaEnd=90;Tf=1.8。在程序中如果满足上述不等式关系,则可以继续运算;如果不满足上述不等式关系,通过算法可以自动调整数值。将程序进行离散化编写[7],仿真结果如图8、图9所示。
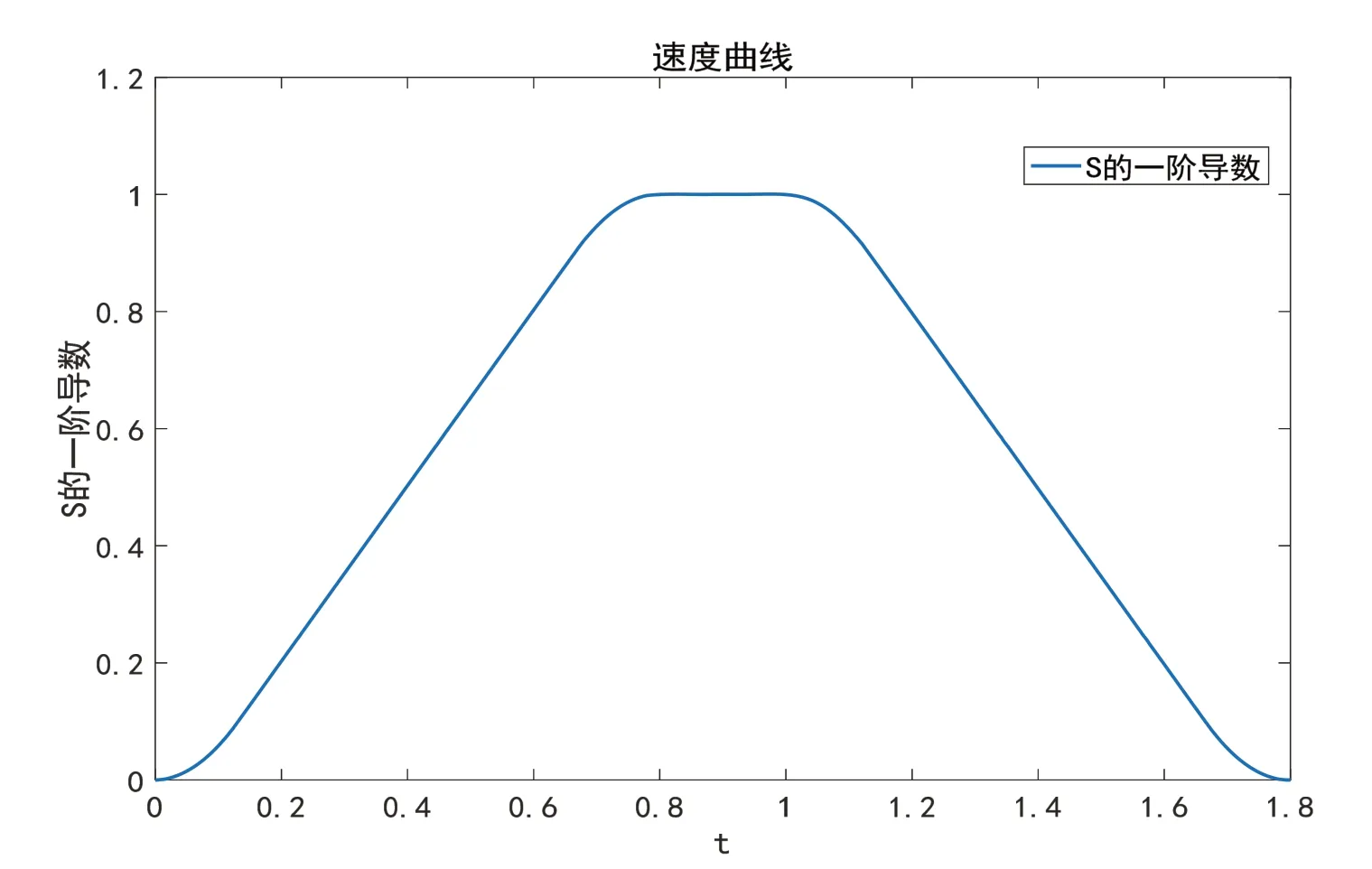
图8 速度曲线图Fig.8 Speed curve
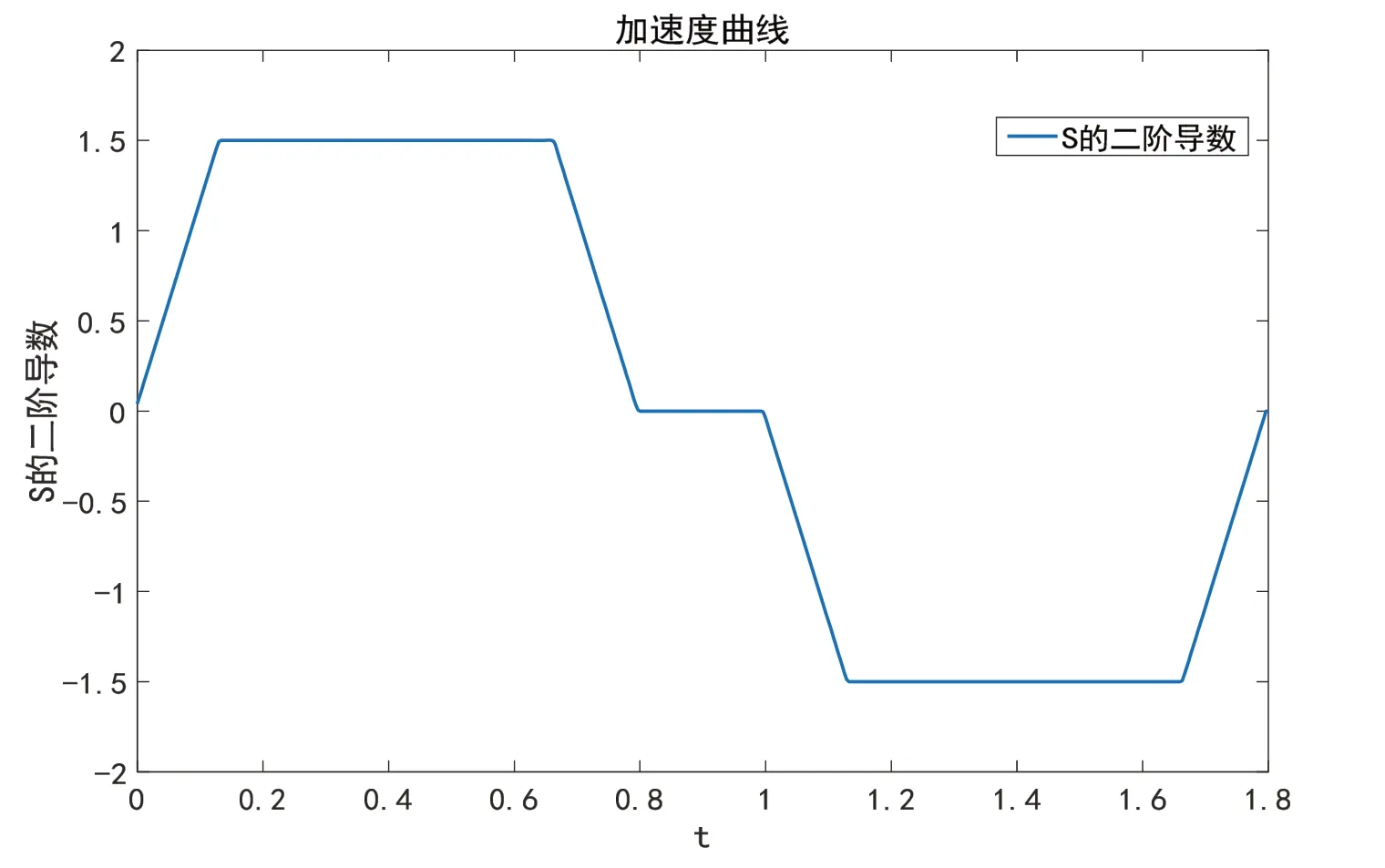
图9 加速度曲线图Fig.9 Acceleration curve
4 结论
在巡检机器人启动和停止的过程中需要采用适当的加减速曲线来对速度进行缓冲,防止瞬时速度对机械本体的冲击。本文利用仿真软件对加减速算法进行仿真分析,通过仿真结果可知S形加减速算法在整个运行过程中最为平滑,加减速阶段不存在突变,但是在实际运行中可能因为达不到最大速度,而不能形成完整的7段式加减速曲线,因此本文提出了自适应S曲线,在算法中加入约束公式,可根据是否满足等式关系来判断S曲线加减速曲线状态,可自动调整数值。该算法应用灵活,可适用于巡检机器人运动控制系统。
引用
[1] 高娟娟.选煤厂智能巡检机器人的设计与研究[J].机械研究与应用,2022,35(01):148-150.
[2] 崔洁,杨凯,肖雅静,等.步进电机加减速曲线的算法研究[J].电子工业专用设备,2013,42(08):45-49.
[3] 宋建国,韩鹏杰,卢意.步进电机S曲线精确控制的研究与验证[J].电机与控制应用,2021,48(11):27-32.
[4] 杨超,张冬泉.基于S曲线的步进电机加减速的控制[J].机电工程,2011,28(07):813-817.
[5] LIU Z,DONG J C,DING Y Y,et al.The Study of S-Shaped Acceleration and Deceleration Curve and the Trajectory Planning Strategy Analysis[J].Key Engineering Materials,2016,693:1195-1199.
[6] 王凯,郑晟.自适应S型曲线对电气布线机的速度规划[J].现代电子技术,2022,45(01):114-118.
[7] 潘海鸿,杨微,陈琳,等.全程S曲线加减速控制的自适应分段NURBS曲线插补算法[J].中国机械工程,2010,21(02):190-195.
