一类非线性四阶椭圆型方程的弱解存在性问题
2022-09-24李秀梅
王 博,李秀梅
(大连交通大学 理学院,辽宁 大连 116028)
0 引言
在广泛的数学及物理应用领域里,椭圆型方程对物理状态的描述、解析和计算提供了基本的模型基础,同时这类方程也在多种应用科学中起到了关键作用.典型的椭圆型方程在物理应用领域中,主要描述电磁场、重力场和反应扩散、能量传导等物理现象.近年来,随着数学理论的不断完善和计算机科学的发展,学者们对椭圆型方程研究出了许多新的成果.陈祖墀等[1-3]利用极小元泛函方法及其他方法对二阶椭圆型方程的弱解存在性进行了讨论.狄华斐等[4]对一类椭圆型方程弱解的正则性问题给出了存在性结论和性质;陈方敏等[5]利用适当的紧性定理和光滑逼近给出了一类椭圆型方程弱解的存在性和唯一性.
不同的方法对不同类型的方程展现了不同的适用性.本文利用构造极小元泛函的方法将陈祖墀[1]提出的低阶方程推广至高阶椭圆型方程,对一类非线性四阶椭圆型方程的弱解进行讨论.
本文讨论如下的四阶椭圆型方程的弱解问题.设Ω⊂Rn是一有界区域,其边界∂Ω充分光滑,在Ω上考虑方程:
(1)
其中:w∈C0(Ω),w>0,p>1.
1 方程弱解的存在性
这一部分中给出方程(1)的弱解形式,同时给出方程(1)弱解的存在性.这里首先给出此方程弱解的定义.
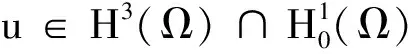
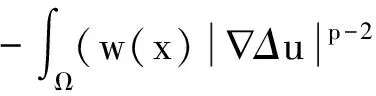
(2)
为了求解方程(1),首先构造相应的泛函,假设存在泛函J(v)满足以下形式,
令
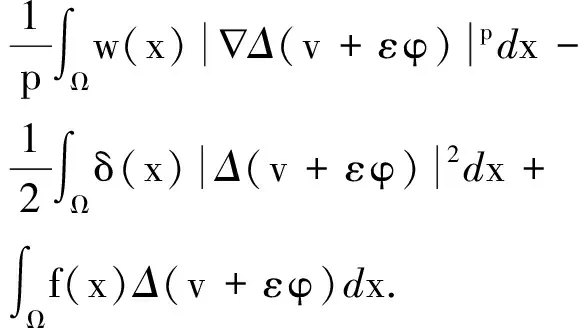

经计算,有
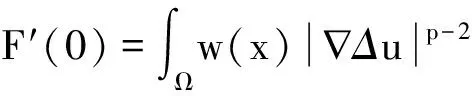
(3)



(4)

其中:k>0是庞加莱不等式中的常数;ε>0为任意常数.
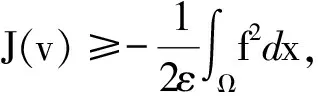
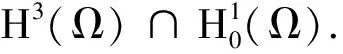


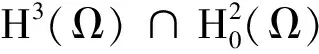
证明根据L2范数的下半连续性得
又由{vk}的弱收敛性,有
则有
(5)



(6)
故
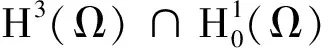
2 方程弱解的唯一性
根据方程(1)已经得到的弱解,在这一部分,给出方程(1)恒存在唯一的弱解.
定理2对任意f∈L2(Ω),方程(1)恒存在唯一弱解.
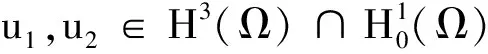
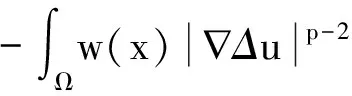
取φ=u,便得
由此可知∇Δu,Δu=0,则利用齐边值条件得u=0.与假设矛盾,故方程(1)恒存在唯一弱解.
3 结语
本文运用构造极小元泛函的方法,给出了泛函的极值元存在性.通过求解泛函的极值解出一类四阶椭圆型方程的弱解问题,并给出弱解的存在唯一性.对椭圆型方程的解法有很多种,例如函数展开法、辅助函数法、Holder估计、全局BMO估计等[6-12].但对于高阶椭圆形方程有诸多局限,极小元泛函可以有效解决高阶椭圆型方程的求解问题.以本文的思路,通过构造极小元泛函的方法可以对阶数更高,形式更复杂的椭圆型方程弱解问题进行研究.
