Controlling acoustic orbital angular momentum with artificial structures: From physics to application
2022-09-24WeiWang王未JingjingLiu刘京京BinLiang梁彬andJianchunCheng程建春
Wei Wang(王未), Jingjing Liu(刘京京), Bin Liang(梁彬), and Jianchun Cheng(程建春)
Key Laboratory of Modern Acoustics,MOE,Institute of Acoustics,Department of Physics,Collaborative Innovation Center of Advanced Microstructures,Nanjing University,Nanjing 210093,China
Keywords: acoustic orbital angular momentum,acoustic metamaterials,acoustic metasurfaces,acoustic communications
1. Introduction
Vortices carrying orbital angular momentum (OAM) are ubiquitously observed in the nature,such as water whirlpools and cyclones. Inspired by those phenomena, many efforts have been devoted to exploring the intrinsic physics of OAMcarrying waves as well as mechanisms for harnessing and making use of them.[1-10]In particular,as an important form of classical wave widely applied in our daily life,acoustic wave is recently demonstrated to also carry OAM,which opens a new degree of freedom for controlling sound and is of considerable significance for both fundamental research and practical applications. In 1974, Nye and Berry for the first time introduced phase singularities in wave physics,and found that the wavefront will twist along the propagation axis,leaving a dark core at the beam center.[11]Such a special kind of beam,known as vortex beam,has a spiral phase dislocation that can be characterized by exp(ilφ)withlbeing the topological charge whose sign indicating the handedness of the helical wavefront andφbeing the azimuthal angle in the propagation cross section respectively,and carries OAM proportional tolwhen the topological charge is non-zero. The twisted phases and amplitudes of vortices of different orders are shown in Fig. 1. Owing to the unique capability of acoustic OAM to transfer mechanical torque contactlessly and acoustic information parallely,the discovery of acoustic vortex beams has opened up possible avenues of applications in object manipulation,[10]imaging,[8,9]ultrasonic alignment,[4]underwater communications,[7]etc.Nevertheless,it remains challenging to make a smooth helical surface with as precisely and versatilely as desired for production and modulation of acoustic OAM,which usually rely on complicated and costly active phased array comprising a large number of individually-addressed bulky transducer arrays and time-consuming postprocessing process[4-7,12]and hence pose limitations on the spatial resolution,device compactness,and information decoding speed.
As a key topic in material physics, design of artificial materials with extraordinary acoustical properties not found in the nature has significantly advanced the field of wave manipulation.[13-18]Driven by the interests to deal with the problem of using bulk metamaterials to control low-frequency sound, in particular, the recent emergence and rapid development of acoustic metasurface enables using a monolayer of unit cells of artificially-engineered structures to fully control the amplitude and/or phase of a sound wave,[19-22]thanks to their unusual characteristics such as with flat profile,subwavelength thickness, low dissipation, and precise wave-steering functionality[21-25]which largely originate from the designed structures rather than the constituent materials. Besides, the development of 3D printing and other additive manufacturing techniques largely facilitates the fabrication of acoustic metasurfaces and relevant experimental demonstrations. When bridging with the discovery of acoustic vortex beams, the emerging technologies of acoustic artificial materials has provided an ingenious way to overcome the challenges in control of acoustic OAM and opened new areas of wave physics,which leads to deeper understanding of various OAM-related phenomena and enables design and innovative application of compact,easy-to-fabricate and lightweight OAM devices with real-time response.
In this review, we first introduce the general linear and angular momentum conservation laws when a paraxial acoustic vortex beam meets at a metasurface with a prescribed phase gradient.We then mainly review recent theoretical and experimental efforts in vortex generation and manipulation with various acoustic artificial structures and discuss their applications such as object manipulation and underwater communication.We conclude with an outlook for the future direction of this emerging field.

Fig.1. The twisted phases and amplitudes of vortices of different orders.
2. Acoustic vortex beams and their interaction with metasurface
The phase dislocation of acoustic vortex beam can be characterized by exp(ilφ)and due to the phase singularity,its amplitude distribution is in the shape of a doughnut. Among many special kinds of vortex beams whose radial intensity distributions can be well described, Bessel beam is a widely known one with the following radial pressure distribution[26]

This important feature allows opening up a new degree of freedom for encoding information in addition to amplitude,phase,frequency,etc.,which have already been extensively employed such as in underwater communication. Besides, the acoustic vortex beam has some unique mechanical properties. The linear and angular momenta (denoted asγandμ, respectively)of acoustic beam at a cross-section perpendicular to the propagation axis can be written as[27]
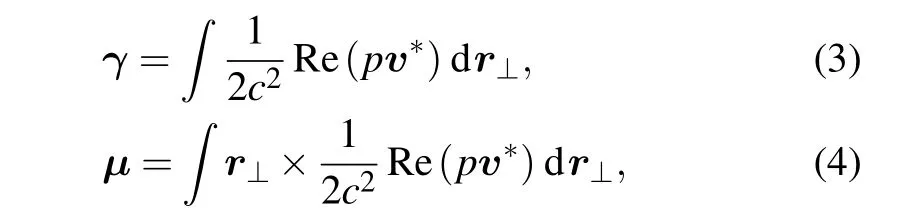
wherer⊥is the two-dimensional(2D)planar radial vector lying in the plane perpendicular to the propagation axis, andpandvare acoustic pressure and velocity respectively. By substituting Eq.(1)into Eqs. (3)and(4), it can be obtained that both linear and angular momentum of vortex beam are along the propagation axis, and if the central axis is chosen as the reference axis, the angular momentum of the vortex beam is proportional to the topological chargel.
It is well known that the refraction and reflection of acoustic plane waves impinging on a conventional planar boundary separating two media obey Snell’s law, which predicts that the angles of incidence and reflection are always equal and that the relationship between the angles of incidence and refraction depends on the difference in the refractive indices of the two media. Acoustic metasurfaces introduce abrupt phase shifts in the acoustic path by adding structures into a planar interface at subwavelength scales, which can control the transmitted and reflected acoustic waves in a manner beyond what is available by conventional interfaces between two natural media.Generalized Snell’s law is derived to describe the relationship between the angles of incident,reflected and transmitted waves at a metasurface,indicating that apart from the difference in the refractive indices,the relationship of reflected and transmitted angles is also dependent of the gradient of the modulated phase added by metasurface.[28]This greatly enriches the researches on acoustic vortices. As a simple yet representative example, a metasurface with azimuthal phase distribution is capable of changing the OAM for acoustic beams. After passing through a metasurface with phase profile ofφ=l'θ, a plane wave can be converted into al'th order vortex beam and, similarly, anlth order vortex beam into anl+l'th order vortex, which is widely used in acoustic vortex generation and demodulation.[29]The underlying physics is that the metasurface with helical phase distribution adds OAM to the acoustic beam,and the magnitude of additional OAM is proportional to the azimuthal phase gradient of metasurface but has no dependence of the OAM carried by the incident beam.
Interestingly, it is recently found that metasurface with phase gradient along one direction (e.g.,xaxis) can also add OAM to vortex beam. In contrast to the above case,the additional OAM turns out to be proportional not only to the phase gradient, but to the OAM carried by the incident beam.[27]When a vortex beam is obliquely incident on a planar interface,the center of gravity of the refractive and reflective beam shows a transverse shift. Based on Snell’s law, angular momentum conservation law can be derived to describe the underlying physics of the refraction and reflection of a paraxial vortex beam on a conventional planner interface.[30]To clearly illustrate the process,two kinds of OAM are is defined:the intrinsic OAM(denoted asj)and the extrinsic OAM(denoted asI)(i.e.,μ=j+I). The former is produced by the azimuthal phase gradient,while the latter is related to the motion of the center of gravity of the beam(notice that only in this section,the extrinsic OAM is defined, because in most cases, more attention is paid to the non-trivial property of intrinsic OAM,and the extrinsic OAM is usually trivial and thus omitted).The refraction and reflection of the vortex beam changes its wave vector,resulting in the change of intrinsic OAM,so it must be compensated by the change of extrinsic OAM,resulting in the transverse shift of the center of gravity of the beam.
When acoustic vortex meets metasurface with phase gradient dΦ/dx=η, the conventional momentum conservation laws are no longer satisfied to describe the behavior of the reflected and refracted beams. A schematic diagram of the reflection and transmission of an acoustic vortex beam on a metasurface is shown in Fig. 2. Combined with plane-wave decomposition method and generalized Snell’s law, it can be obtained that the gravity center of reflected and transmitted beam shows a transverse shift proportional to the topological charge of acoustic vortex beam,which can be divided into two parts:

wherekis the wavenumber,and the superscriptsa=i,r,andτrefer to the incident,reflected and transmitted beams,respectively.nr=n1,nτ=n2are the refractive index indices of the medium 1 and medium 2 (na=c0/cawithc0being the reference sound speed),ξa= cosθi/cosθa,νa= sinθi/sinθa,θarepresents the angle betweenzaaxis andzaxis, andQais acoustic energy reflection and transmission coefficients of plane wave. The second part is dependent of the reflection or transmission coefficient and can be understood as a reflection and transmission coefficients modulation part. Here we focus on the first part,which shows the change of extrinsic and intrinsic OAM. The linear momentum and intrinsic OAM ofath vortex beams are defined asγaandjarespectively,while the linear momentum and the angular momentum provided by metasurface are defined asγmetaandjmetarespectively, and the generalized conservation law can be described as


where subscriptsnandtrefer to the normal and tangential components. Then the tangential linear momentum and normal angular momentum provided by metasurface can be obtained

whereViis the integration of acoustic energy of the incident vortex beam over the cross-section perpendicular to the propagation axis. Equations(8)and(9)indicate that the linear momentum provided by metasurface is independent of the incident angle and the topological charge, while the angular momentum provided by metasurface depends on the incident angle and topological charge. Both linear and angular momenta are proportional to the phase gradient. When incident wave does not carry OAM(i.e.l=0),the transverse shift will disappear, and metasurface only provide linear momentum, which coincides with the case of a Gaussian beam interacting with a metasurface.

Fig.2. Schematic diagram of the reflection and transmission of an acoustic vortex wave on a metasurface generating a constant gradient of phase along x-direction.[27] (xa,y,za)denote the coordinate frames of individual beams,with za axis attached to their directions of propagation. The superscripts a=i,r,and τ refer to the incident,reflected,and transmitted beams,respectively. zi is perpendicular to the y axis. θa represents the angle between za axis and z axis.The reflected and transmitted beams have the gravity centers shifted along y axis. Reproduced with permission from Ref.[27].
3. Generation of acoustic OAM
One basic question in the study of acoustic OAM is the mechanism for simple, efficient and precise production of OAM-carrying beams. This is pivotal for their practical application given the fact that an individual transducer used in existing methods is generally able to produce an acoustic beam carrying no OAM such as a Gaussian beam. Conventional techniques usually rely on active phased array composed of numerous individually-addressed transducers to generate OAM beam,such as hexagonal arrays[31]and uniform circular transducer arrays,[32,33]yet the smooth phase of OAM beams, especially of a high order, need to be produced at the cost of expensive and complicated systems. Hence the passive artificial structures provide a simpler and less expensive alternative for modulating acoustic vortices.
3.1. Generation of acoustic OAM based on diffraction
In 2004, Gspanet al. proposed the use of photoacoustic effects to generate vortex acoustic waves by irradiating a laser on an absorber with a spiral gradient thickness so that the other side of the absorber can be excited with a spiral phase of the outgoing acoustic waves.[34]Ealoet al. proposed and experimentally demonstrated a method to generate a vortex sound field in air using cellular ferroelectrets.[35]Such materials have the advantages of highd33piezoelectric coefficient,large operating bandwidth,and low acoustic impedance,which are conducive to achieving a balance between directivity, sensitivity and cost,and can better achieve acoustic matching with air. In addition,it has high plasticity and can be used to manufacture transducer structures with various flexible surfaces.
The aforementioned mechanism of using helical thickness can only design a single-frequency effective vortex field transmitter,and the thickness needs to be modulated,meaning that it cannot have a flat profile at both the entrance and exit ends. Furthermore, the generated acoustic vortex fields are usually only able to keep the topological number stable over short distances. To generate acoustic vortices with planar and thin plane,Jianget al. designed a planar acoustic vortex emitter formed by the coupling of subwavelength helical slits by utilizing the diffraction effect of structure on acoustic waves,and generated the acoustic vortex with topological stability in a wide frequency range in theory and experiment for the first time.[36]Figure 3(a) is a schematic diagram of the principle of acoustic vortex transmitters with different numbers of spiral arms, and the phase and sound intensity diagrams of the generated vortex fields. It can be seen from Fig.3(a)that for devices with 1 to 4 spiral arms respectively, when interacting with an incident acoustic wave of a specific wavelength, the phase changes in a loop are 2π,4π,6π,and 8π,respectively,corresponding to the topological charge numbers arel=1,2,3, and 4, indicating that the design can control the order of the vortex field by adjusting the number of spiral arms. Figure 3(b)is a comparison diagram of the experimental and simulation results of the phase distribution of the vortex field at different frequencies and different propagation distances. The results of experimental measurements and theoretical calculations are in good agreement,proving that the designed vortex emitter can operate in a wide frequency band and generate a topologically stable acoustic vortex field over a long distance.A series of work of vortex generation revolves around this mechanism. Jim´enezet al. successively obtained high order Bessel beams using a multiple-arm Archimedes spiral diffraction grating(Fig.4(a))and generated strongly focused vortex beams by Fresnel-spiral zone plates, which combines the focusing properties of a Fresnel zone plate and the phase dislocation of spiral gratings(Fig.4(b)).[37,38]Jiaet al.achieved fractional acoustic vortex using artificial structure plates engraved with discrete Archimedean spiral slits(Fig.4(c)).[39]Recently,Caoet al.proposed an improved hybrid single-arm coiling slit to generate vortices. They combined equiangular spirals and Fermat spirals to increase the transmission area of the acoustic waves and enhance the transmission of the generated vortex.As a result,the generated vortex is characterized by weak focusing and a deeper potential well in the center(Fig.3(d)).[40]To increase the flexibility,Muelas-Hurtadoet al.demonstrated the simultaneous airborne generation of vortex Bessel beams with different topological charges,separated among each other along the propagation axis,using a single-arm/two-arm active spiral source(Fig.4(e)).[41]

Fig.3. Schematic and experimental results of acoustic vortex emitter:[36] (a)schematic diagram of the structure of an acoustic vortex emitter with different numbers of spiral arms and phase and intensity distribution of the vortex field generated in the plane of a specific position;(b)comparison of experimental and simulation results of vortex field phase distribution at different frequencies and different propagation distances. Reproduced with permission from Ref.[36].

Fig. 4. Schematic diagram of the designs of various diffraction-based artificial structures for OAM generation and their efficient: (a) a high order Archimedes’spiral grating;[37](b)a Fresnel spiral zone plate generating sharp-focused vortex;[38](c)the artificial structure plate engraved with discrete Archimedean spiral slits and basic unit for the fractional acoustic vortex;[39](d)hybrid single-arm coiling slit modulating acoustic waves;[40](e)phase of acoustic vortex beam in different distances generated by active diffraction gratings.[41]Panels(a)-(e)are reproduced with permission from Refs.[37-41].
3.2. Generation of acoustic OAM by metasurface

Fig.5. Schematic and experimental results of acoustic vortex generation by metasurface.[29] (a)Schematic diagram of the principle of OAM generation using metasurface to excite acoustic resonance;(b)realization of metasurface for planar resonance layers;(c)schematic plot of the internal structure of a single unit; (d)spatial acoustic pressure distribution obtained by numerical calculation and(e)phase distribution and(f)sound pressure distribution obtained by experimental measurement in two different planes in the far-field region. Reproduced with permission from Ref.[29].

Fig.6. Schematic diagram of various metasurface-based designs of OAM generators:(a)a metasurface with units composed of two resonators and three necks;[42] (b)a metasurface composed of helical-structured units;[43] (c)annulus acoustic metasurface based on composite labyrinthine structures;[44](d)a multi-bit coding acoustic metasurface with units structured as Helmholtz resonators;[45] (e)a metasurface based on coupled Helmholtzresonators for generating high-order acoustic vortex field;[46] (f) a continuously tunable metasurface;[47] (g) schematic plot of the broadband acoustic vortex beam generator;[48] (h) non-local metagrating for generating acoustic vortex;[49] (i) dual-layer phase gradient metasurface for asymmetric vortex generation.[50] Panels(a)-(i)are reproduced with permission from Refs.[42-50].
The mechanic based on the acoustic diffraction requires bulky size in both the thickness or transverse directions and the structure itself must have the geometric characteristics of a spiral distribution. In addition,the transmission efficiency of the acoustic energy is also limited,and the generated acoustic vortex fields are usually only able to keep the topological number stable over short distances. Therefore,how to use small-scale planar simple non-helical structure to efficiently generate stable acoustic OAM is a key scientific problem that needs to be solved. In order to increase the potential of OAM generators’minimization and integration,a new physical mechanism was proposed for the generation of acoustic OAM:instead of relying on the incident phase or propagation distance which varies with azimuthal angleφ, the efficient wavenumberkeffin the structure is directly manipulated to have a special dependence on the azimuthal angle.[29]It can be seen intuitively from Figs. 5(a)-5(c) that the incident plane wave is axisymmetrically distributed,and its incident phase has no dependence on the azimuthal angleφ, and in the designed non-spiral plane structure, the acoustic wave propagation distance is also a constant, with no dependence on the azimuthal angleφ. But by exciting a suitable acoustic resonance in the plane resonance layer, the effective wavenumberkeffdistributed along the angle direction can be generated, and finally an acoustic vortex field with a specific order can be formed. Based on this, an acoustic metasurface is designed and manufactured which consists of resonators supporting hybrid resonance for overcoming the impedance mismatch against surrounding air and can thereby modulates the wavenumber freely while keeping a high energy transmission. Such structure generated acoustic vortex fields of a predetermined order efficiently and accurately in both theory and experiment (Figs. 5(d)-5(f)).A series of designs have later been proposed for generating acoustic OAM based on the use of metasurfaces. Yeet al.proposed to convert plane waves into vortex beams with OAM by using a metasurface with a scale smaller than the wavelength,and verified the effect of the vortex beam on the moment of a foam acoustic disc, proving that this method can generate acoustic moment simply and efficiently (Fig. 6(a)).[42]Esfahlaniet al.further compressed the thickness of the OAM artificial device to 1/3 of the wavelength by designing a metasurface based on a helical structure(Fig.6(b)).[43]Jiaet al.designed an annulus acoustic metasurface based on composite labyrinthine structures and generated the airborne fractional acoustic vortices (Fig. 6(c)).[44]Zhanget al.generated vortex beam by multi-bit coding acoustic metasurfaces, whose coding units structured as Helmholtz resonators with different geometric parameters (Fig. 6(d)).[45]Guoet al.generalized the resonance-based method similar to Ref. [29] to generate high-order and multiplexed acoustic vortices (Fig. 6(e)).[46]Fanet al.designed a continuously tunable acoustic metasurface with changeable helical depth to generate high-order OAM and decreased thickness of the metasurface down to less than 1/4 wavelength(Fig.6(f)).[47]To increase the propagation distance of the generated vortex,a quasi-three-dimensional reflected metasurface is designed by Wanget al.,which enables the acoustic vortex to propagate longer than 9.2λin free space(Fig. 6(g)).[48]Recently, Houet al.presented a strategy to generate highly efficient vortex beams via nonlocal acoustic metagratings in cylindrical waveguides. By harnessing the nonlocality,they fully controlled the topological charge of the scattering vortex mode with a conversion efficiency of more than 99% (Fig. 6(h)).[49]Fuet al.theoretically proposed a mechanism of asymmetric generation of acoustic vortex and experimentally demonstrated through dual-layer phase gradient space-coiling metasurfaces(Fig.6(i)).[50]
3.3. Generation of acoustic OAM in 2D space
In comparison to the aforementioned OAM production in three-dimensional (3D) space, the transverse OAM carried by a 2D vortex field offers greater advantages in areas such as surface particle manipulation and on-chip communication. The vortex field in the 2D system also has a spiral phase dislocation and a donut-type sound field intensity distribution, however, unlike the 3D vortex field with OAM parallel to the propagation direction, the direction of OAM in the 2D system is perpendicular to the wave vector, and its basic generation mechanism is also different. The 2D vortex generation can be classified into out-of-plane excitation and in-plane excitation depending on the spatial dimension where the incident source is located. Compared with out-ofplane excitation,[51,52]in-plane excitation methods offer a simpler and more compact alternative for generating high-quality pure OAM modes. However, this method usually requires a large number of independently addressable transducer units to construct a toroidal array to achieve in-plane direct introduction of OAM,[5,53,54]which is costly,complicated and energy consuming. Furthermore, the bulky size of active elements usually cause spatial aliasing effect in a ring closing to the transducer, which becomes more severe when the centers of vortex and device are not perfectly aligned. To generate non-aliased 2D acoustic vortex,metasurface is introduced as a low-cost alternative by Liuet al.(Fig. 4(a)) with advantages in terms of simplicity, resolution, efficiency, compactness,and energy consumption.[55]They rigorously derived the boundary conditions for generating the desired mode of 2D acoustic vortex without aliasing,which is implemented by designing subwavelength unit cells with phase engineering capability and high transmission efficiency. Figure 7(a) shows the performance of their scheme to precisely generate a nonaliasing 2D vortex by using a compact,passive device,as evidence by the undistorted Bessel-like pattern extending to the whole inner region. Later, to eliminate the reliance on the waveguide system and geometric axisymmetry, they further proposed a mechanism for generating 2D vortex of airborne sound on an unbounded surface decorated with ultrathin structures in free space, and experimentally demonstrated a simple design of unit cell capable of exciting evanescent wave in a square area with arbitrarily modulated transmitted phase(Fig. (7(b)).[56]Later, to improve the efficiency of 2D OAM production, Liet al.demonstrated a mechanism that uses cylindrical bianisotropic metasurfaces to transform wavefront with nearly 100%efficiency(Fig.7(c)).[57]On the basis of the discovery of the important phenomenon of chirality-reversal radiation at an exceptional point, a mechanism is proposed by Chenet al. for producing a 2D vortex by using a single speaker placed within a passive ring cavity with parity-timesymmetric modulation of the refractive index[58]as schematically shown in Fig.7(d),where the coalesced eigenstate was constructed in the counterclockwise mode. Recently,they further used such a mechanism to radiate the 2D vortex in the cavity to 3D space by a slit,which enables to emit acoustic vortex beam with switchable OAM but free of system reconfiguration,providing a new scheme for 3D vortex generation.[59]
To further overcome the dependence on geometric symmetry and non-Hermicity of the system, Liuet al.proposed a mechanism for producing a 2D vortex from a single sound source. They derived a rigorous criterion for excitation of a single angular momentum mode in the cavity using the mode analysis method and the inverse solution method, and broke the dependence on the 360°omnidirectional phase boundary by introducing a passive reflective acoustic boundary, which is important for the miniaturization and integration of on-chip OAM devices. Based on an equivalence between the physical boundary and a virtual boundary with perfect azimuthal symmetry,general boundary conditions were derived for the excitation of the desired order OAM modes in arbitrarily shaped conditions(Fig.7(e)).[60]

Fig.7. Schematics of various types of mechanisms for 2D OAM production: (a)a circular metasurface for generating non-aliasing 2D OAMs;[55](b)generating a 2D acoustic vortex on an unbounded surface;[56] (c)efficient 2D OAM conversion by bianisotropic metasurface;[57] (d)schematic plot of the passive acoustic parity-time-symmetric ring cavity for generating 2D acoustic vortex;[58] (e) virtual boundary transformation and simulated normalized acoustic pressure of 2D vortex distribution inside a pentagram region.[60] Panels (a)-(e) are reproduced with permission from Refs.[55-58].
4. Manipulation of acoustic OAM
Current applications based on vortex sound field has shown promising prospects in many fields, it is therefore of particular importance to manipulate acoustic vortices as desired to meet the requirement in the application scenarios.Here we focus on two major aspects of acoustic vortex manipulation: modulation of the vortex field itself,including focusing,asymmetric transmission,etc.;identification and sorting of vortices of different topological charges of composite vortices to meet the requirements of extracting information carried in the acoustic vortex beam in communication which would be pivotal for the encoding and decoding of information carried by OAM beams in acoustic communication.
4.1. Modulation of acoustic OAM
In practical applications,acoustic OAM is often required to be modulated to meet the needs of particular scenarios.As a typical example, the convergence of OAM beam is important for enhancing the mechanical effect in object manipulation and improving the information transfer distance in high-capacity communication. In a 3D system, Jim´enez-Gamb´ınet al. used acoustic holograms to realized transcranial focusing of ultrasonic vortices, which paved the way to designing low-cost particle-trapping systems, clot manipulation,and the exertion of acoustic-radiation forces and torques in the brain for biomedical applications (Fig. 8(a)).[61]To meet the requirements of 3D trapping,Baudoinet al. demonstrated a flat holographic transducer to fold a focalized spherical acoustic vortex (Fig. 8(b)).[62]They generated spherical vortex beams materializing the intersections between the Hankel beam isophase surfaces and a plane with metallic electrodes deposited at the surface of a piezoelectric substrate.Such vortex field can be used to realize 3D particle trapping which is not possible with cylindrical acoustic vortices. To overcome the diffraction limits which hinders the precision of acoustic OAM manipulation and their applications such as in on-chip devices, Liuet al. proposed to focus 2D vortex for airborne sound beyond diffraction limit on an ultrathin open surface (Fig. 8(c)).[56]A simple design of unit cell was presented as a practical implementation, which is capable of exciting evanescent wave and modulating its propagation phase over full 0-to-2πrange. By analytically deriving the dispersion relationship and desired azimuthal distribution of effective parameters,they elucidated how to guide the propagation of excited evanescent waves in the vicinity of an unbounded surface decorated with designed structures and focus such surface vortex within a target region despite its compactness and nonaxisymmetry.
To extend application of vortex in particle manipulation,Jianget al.introduced the asymmetry to acoustic vortex beam in a homogeneous media by the superposition of symmetric Bessel modes on the source plane.[63]They achieved modulation based on the theoretical design of non-diffractive asymmetric acoustic vortex beams and implemented such modulation with acoustic metasurfaces. Recently, the proposal of acoustic OAM asymmetric transmission using metagratings with gradient phase provides new opportunities for manipulating sound vortices (Fig. 8(d)).[64]It is found that, depending on a critical topological charge,incident acoustic vortices can either transmit through metagrating with the lowest diffraction order or take higher diffraction orders with the transmission and reflection depending on the integer parity of metagratings. Based on this, asymmetric transmission preserved with the identical topological charge.

Fig. 8. Schematics of modulation of acoustic vortices: (a) transcranial focusing of ultrasonic vortices by hologram;[61] (b) focalized spherical acoustic vortex generation;[62] (c) focusing 2D vortex beyond diffraction limit;[56] (d) the effect of vortex asymmetric transmission.[64] Panels(a)-(c)are reproduced with permission from Refs.[56,61].
4.2. Recognition and sorting of acoustic OAM
Provided the important capability of acoustic OAM to serve as information carrier,recognition and sorting of acoustic OAMs in a fast and precise manner is of fundamental significance for efficient and accurate extraction of information carried by OAM beams, which would be also a key requirement for diverse practical applications such as acoustic communication. Due to the orthogonality between different OAM modes, Shiet al.used the inner product operation in the post-processing to separate the multiplexed OAM modes received by a complicated transducer array.[7]To realize realtime separation of different OAM modes, Liuet al. proposed and experimentally validated a passive system constituted of two composite helical waveguides to separate acoustic vortices with opposite OAM topological charges, providing a simple method for OAM demultiplexing (Fig. 9(a)).[65]To achieve fast, efficient, and parallel OAM state separation,Jianget al. designed reflective and refractive prisms to convert the vortex beam of the helical phase into a plane wave with different transverse phase gradients using the acoustic parabolic phase metasurface (Figs. 9(b) and 9(c)).[66,67]To effectively improve the signal-to-noise ratio, spectral/spatial selectivity and device compactness, Liuet al. designed and experimentally demonstrated an acoustic monolayer ultrathin metadecoder to achieve real-time decomposition of multiple OAMs in free space.[68]They proposed an effective mechanism for simultaneous wavefront inverse distortion and beam shaping,based on which the propagation direction and detection position of each demodulated beam can be independently and arbitrarily modulated. As shown in Fig. 10, when a synthesized OAM beams composed of multiple orders of coaxial vortices is incident normally on the metadecoder, the wavestructure interaction will automatically and parallely sort different OAM beams into the prescribed focal positions with enhanced intensity after removing their vortex patterns. Figure 10(b) illustrates the anti-helix spatial phase for OAM removal and the focusing phase for converging the energy of outgoing demodulated beam to desired foci, which collectively achieve multi-mode decomposition of OAM. In experiments,they designed a metamaterial building block which uses the coupling between a straight channel and four resonators to satisfy the required surface phase distribution. To reduce the dependence of decoding accuracy on alignment between the beam and the decoder,Wenget al.proposed an inherently different mechanism[25]by constructing an array with artificial structural units(the parameters of each unit are obtained from a machine learning training). Their designed structure mimics the function of a conventional neural network and, instead of utilizing the OAM orthogonality as in previous mechanisms,directly recognizes the order and information from the complicated spatial patterning of a synthesized vortex. More importantly, their mechanism stands regardless of whether the centers of the beam and device are perfectly overlapped. As shown in Fig.11,a four-layered artificial structure is designed to recognize a maximal combination of 8 OAM orders with their centers transversally misaligned in arbitrary directions by a maximal distance of 6λ, which reaches 1/3 of the side length of each meta-neuron layer and would be quite challenging for existing mechanisms using equal-sized devices. As a consequence,they realized realtime and passive recognition of each mutually-orthogonal OAM states by using such system that features controllable output regions and high robustness against misalignment along both the axial and transverse directions.

Fig. 9. Schematics of OAM sorting and recognition: (a) acoustic OAM splitter;[65] (b) 2D refractive prism for OAM recognition;[66] (c) 2D reflective prism for OAM recognition.[67] Panels(a)-(c)are reproduced with permission from Refs.[65-67].

Fig. 10. Schematic diagram and the sorting principle of metadecoder:[68] (a) schematic plot of the metadecoder for parallel demultiplexing of a synthesized vortex beam (with orders of -1, +1, and -2 as an example); (b) schematic diagram of derivation of phase profile in the decoding surface for the above three-channel system. Reproduced with permission from Ref.[68].

Fig.11. Schematic and recognition results of misaligned vortex by acoustic meta-neural-network.[25] (a)Schematic of the recognition of a multiplexed OAM beam (with l =+3, ±4 and a misalignment distance of 6λ as an example) by the designed artificial structure that redistributes the incident energy on the detection plane in a way such that whether or not each OAM state can be unambiguously marked; (b) the dependence of recognition accuracy on the distance and direction of misalignment. Insets: the spatial patterns of a misaligned(top)and an aligned(bottom)OAM beams with the same OAM order;(c)the simulated recognition accuracy as a function of axial distance.
5. Application of acoustic vortex
The OAM carried by the vortex field and the resulting acoustic radiation force and moment have been widely studied due to the potential applications in diverse scenarios such as object manipulation. In 2011,Zhang and Marston theoretically analyzed the magnitude of the acoustic radiation moment of a vortex field on an axisymmetric absorbing object[1]and arrived at a conclusion that the ratio of the OAM flux density and energy flux of a vortex field is equal to the ratio of its topological charge and the angular frequency. Mitriet al. focused on the acoustic scattering from spheres in ideal Bessel traveling and standing wave fields,and analyzed the acoustic radiation moments of vortex acoustic fields on spherical scatterers under different conditions.[2]Anh¨auseret al.investigated the radiation moments generated by vortex sound fields in viscous fluids and quantitatively measured the conversion of OAM to absorbers in liquids.[3]These theoretical results suggest the possibility of building novel devices that use the mechanical effects of acoustic vortex to manipulate objects. Two of the most typical examples are the“acoustic tweezers”[69]and the“acoustic wrench”.[70]The acoustic potential trap at the vortex center allows trapping and precisely manipulating tiny particles much smaller than wavelength. In addition, through the wave-matter interaction, the vortex beam carrying OAM can apply a rotational torque contactlessly, enables new acoustic devices such as acoustic motors and centrifuges. On the other hand,due to the high absorption and strong scattering of electromagnetic and optical waves underwater,acoustic wave is so far the only information carriers for underwater long-distance transmission,with diverse applications ranging from in numerous activities such as marine scientific research and military.However, the inherent low frequency and low wave speed of acoustic waves severely limit the bandwidth and transmission efficiency of underwater acoustic communication. The introduction of OAMs with innate orthogonality with each other and frequency into the acoustic system is expected to open a new degree of freedom for encoding information and have great potential for high-speed and high-capacity communication applications.
5.1. Object manipulation with acoustic OAM
Object manipulation based on acoustic vortex fields has shown promising prospects. Although most researchers in the field of object manipulation with acoustic OAM use active phased array methods, acoustic metasurface techniques still have a role to play. Yeet al.proposed to convert plane waves into vortex beams with OAM by using a metasurface and experimentally verified the effect of the vortex beam on the moment of a foam acoustic disc.[42]Later, Wanget al.experimentally demonstrated the mechanical effects of vortex acoustics carrying OAM for applications such as particle selfpatterning.[71]An Archimedean spiral grating was etched on the back side of a brass plate (Fig. 12(a)) and placed in front of a high-intensity focused ultrasound (HIFU) transducer. In the laboratory tank, polystyrene particles with radius much smaller than the wavelength were placed on the surface of the brass plate, and the particles were distributed in a circular pattern after being stabilized by the acoustic radiation force (Fig. 12(b)). When a millimeter-scale polylactic acid disk is suspended above the brass plate, the sound-absorbing disk rotates around the central axis under the action of acoustic OAM.It was found that the moment generated by the acoustic beam was proportional to the product of the acoustic energy absorbed by the polylactic acid disc and the order of the OAM carried by the acoustic beam,and inversely proportional to the frequency of uniform rotation of the disc, which could be used to estimate the magnitude of the moment effect of the vortex acoustic beam on the object. To further increase the rotation speed,Liet al.used spiral grooved plates to achieve high-speed rotational manipulation of underwater foam discs,spheres and rods.[72]By experimentally analyzing the acoustic radiation torque of the first-order and second-order acoustic vortex beams through the rotational manipulation of a standard acoustic absorption disk,they concluded that the rotation speed of the disk driven by the second-order acoustic vortex beams is almost twice of that driven by the first-order acoustic vortex beams and a linear relationship between the radiation torque and electrical power(Figs.12(c)and 12(d)).
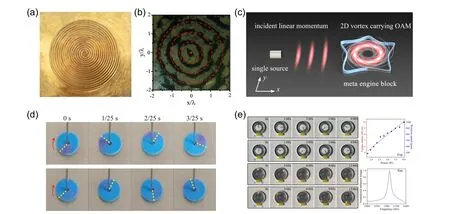
Fig.12. Sample of spiral shape structure and the results of particle manipulation and rotating objects. (a)Sample of brass plate with spiral shape structure;[71] (b) snapshots of particle manipulation;[71] and photograph of the disk rotation process driven by the first-order (c) and the secondorder(d)acoustic vortex beams at the same time interval;[72] (e)schematic plot of compact ultrasonic motor;[60] (f)clockwise and anticlockwise rotation of a foam disk and a small ball using 4th-order and -4th-order 2D vortex beams produced by metasurface.[60] Panels (a) and (b) are reproduced with permission from Ref.[71]. Panels(c)and(d)are reproduced with permission from Ref.[72].
Baudoinet al.demonstrated a miniaturized selective acoustical tweezer by folding a focalized acoustical vortex on a flat holographic transducer with spiral metallic electrodes (Fig. 8(b)).[62]The shape of the electrodes is an Archimedes-Fermat spiral, an intermediate situation between the Archimedes spiral and the Fermat spiral. The radial contraction of the spiral is able to generate focused spherical vortex beams without the requirement of a curved transducer or a lens. They demonstrated the high selectivity of this tweezer by measuring the acoustic field with a laser interferometer and quantifying the fast radial decrease of secondary rings and by selectively trapping and moving one particle independently of its neighbors in a standard microfluidic environment. Such methodology with no need of a 2D system,bulky device size,geometric symmetry, active elements, or complicated phased array to offer new possibilities for the miniaturization and integration of planar vortex devices. To increase the levitation force in 3D particle trapping,Liet al. demonstrated a kind of 3D acoustic tweezers with vortex streaming using a 2D PDMS lens, which combines the radiation force for trapping in two dimensions with the streaming force and expands the range of particles that can be manipulated.[73]Yet these existing mechanisms usually need to rely on produce acoustic OAM from out of plane to manipulate different objects. To reduce the dimensionality of object manipulation to 2D as well as promote the potential of miniaturization and integration of OAM-based devices,Liuet al. proposed a compact,ultra-thin and passive artificial acoustic motor for efficient conversion of unidirectional linear momentum to OAM in 2D system, as shown in Fig. 12(e).[60]The acoustic motor is made of a meta engine block based on an acoustic metamaterial, and the boundary conditions of the device are manipulated based on theoretically derived strict criteria such that the vortex beam carrying OAM can be efficiently excited in the designed motor,increasing the sound intensity of the Bessel-type field by more than 10 times compared to the incident wave radiated by a single source. Thanks to the efficiency of this mechanism,the acoustic motor can provide a significant acoustic radiation moment and drive the load rotation up to 1000 rad/min (Fig. 12(f)).More importantly,their mechanism enables arbitrary design of geometry of the boundaries as required. This artificial acoustic motor working for a single source with flexibility and efficiency opens a novel route for acoustic manipulation in 2D regime, which is important in the fields of particle manipulation and information transmission on the surface.
5.2. Underwater communication with acoustic OAM
In 2017, Shiet al.proposed an acoustic OAM communication technique based on active transducer arrays,[7]where they used a 4-loop 64-array element OAM transmitter to radiate a composite vortex acoustic field containing 8 topological orders, and used another acoustic phased array at the demodulation end to measure and post-process the acoustic field thus extracting the OAM information of the spatial acoustic field,achieving efficient and accurate coding and decoding of OAM loading information. Jianget al.carried out simultaneous research work on acoustic OAM-based signal transmission techniques for demultiplexing modulation of vortex acoustic beams with metasurfaces in the one-dimensional waveguide regime(Fig.8).[74]This passive metamaterial-based demodulation mechainsm does not require the use of a large number of transducer phased arrays or spatially scanning of acoustic fields at the receiver side, nor does it rely on any computeraided post-processing of the received signal. Instead, such a mechanism is a real-time demodulation technique that does not require any signal processing and does not have any time delay. A phased array of 8 transducer units is used at the transmitter side to transmit the synthetic OAM beam carrying the information, and OAM beams of different orders are used directly as information carriers. At the receiver side,the principle of real-time demodulation is based on passive metasurfaces. In a previous work,[29]it has been shown that OAM can be introduced to the acoustic regime using metasurfaces,then when such structures interact with the OAM acoustic beam,the OAM-carrying vortex sound field can in turn be transformed into an OAM-free plane wave (Figs. 13(a) and 13(b)). For a system that uses a total ofNorders of OAM beams for encoding, by placingNidentical de-multiplexing metasurfaces(each designed to reduce the topological charge by 1 order)at the receiving end,the OAM beams can be transformed into order-varying OAM beams or plane waves, ultimately ensuring that each order of the OAM beam is transformed into a plane wave at a specific location. In this demultiplexing mechanism, they skillfully exploit the usually considered trivial property of the null center of the OAM beam, which plays a key role in the separation mechanism of OAM beams of different orders. As shown in Figs. 13(c)and 13(d),the experimental results show that this OAM communication technique can maintain a very high transmission accuracy in the case of single-sensor measurements because it does not require the complete measurement of the entire vortex field information and subsequent signal processing. Later Sunet al. proposed underwater acoustic multiplexing communication by pentamode metasurface based on similar demultiplexing mechanism.[75]
However, the OAM multiplexing strategies mentioned above rely on multiple coaxially-overlapped twisted beams used as orthogonal communication channels. In such cases,the channel number has to be increased by including more high-order OAM modes, leading to more severe diffraction and spatial aliasing effect, which limits the maximum number of available communication channels. Recently,Wuet al.proposed a mechanism using multipath sound twisting to realize real-time high-capacity communication free of signalprocessing or sensor-scanning and experimentally validated it using metasurfaces.[76]As shown in Figs. 14(a)-14(c), they establishedNtransmission paths betweenNpairs of transmitting and receiving units.Each transmitting unit emits a synthesized acoustic beam formed by coaxially overlapping vortices with different orders, which are used as independent channels for encoding different information. After passing over the metasurface, the OAM patterns of each order in different transmission paths will be removed and further transformed into multi-focused beams with different focal positions. It is worth mentioning that the designed metasurface with strong spatial selection (i.e., any oblique incidence of vortex beam will not notably affect the acoustic intensity at the prescribed focal points) and ability of energy convergence enable guarantees low crosstalk and high signal-to-noise ratio for this decoding mechanism while dramatically expanding the channel capacity. They experimentally showcased a more practical example of real-time transmission of a complicated binary image.As shown in Figs.14(d)-14(f),the target image is divided into four parts and transmitted through four OAM channels simultaneously. By assembling four measured data streams received at four prescribed focal points together, they obtained the output image and plot the results in Fig.14(g), which exhibits the high quality of image transmission.

Fig.13. Schematic and experimental results of acoustic OAM multiplexing and de-multiplexing.[75] (a)Schematic representation for multiplexing and de-multiplexing;(b)equiphase surfaces of pressure for the 1st order OAM beam transmitting through de-multiplexing metasurface in waveguide;(c)experimentally and numerically received high-speed data flow;(d)image reconstructed from the assembled data stream both in simulation and experiment. Reproduced with permission from Ref.[75].

Fig. 14. Schematic and experimental results of free-space acoustic communication with high spatial information density by multi-path twisting of acoustic wave.[76] (a) Schematic diagram of the designed communication system; (b) the schematic plot of simultaneous demultiplexing of synthesized vortex beams;(c)simulated phase shift and transmission provided by the metamaterial unit cells with different structural parameters;(d)the original input image which is divided into four separate parts for a parallel transmission;(e)the enlarged view of square region marked by red line in panel(d);(f)the target and output data streams of four lines in panel(e);(g)the output image reconstructed from four data streams.
6. Conclusion and outlook
The introduction of OAM for acoustic waves has opened up new degrees of freedom in acoustic manipulation and has become a hot issue in physics in recent years. In contrast to conventional active and passive methods that depend on the spiral azimuthal dependence of incident phase or propagation distance, the recent development of acoustic artificial structures, particularly the advances in acoustic metasurfaces with high efficiency, flat profile and versatile functionality, has injected new energy into the study of acoustic OAM generation and manipulation. The study and utilization of acoustic OAM is not only of fundamental academic significance,but also has promising applications in various important situations. The generalized momentum conservation laws governing the interaction of an acoustic vortex beam with a metasurface reveals that the total OAM comprises the intrinsic and extrinsic OAMs and that the incident angle and topological charge only affect the angular momentum provided by metasurface while both the linear and angular momenta are proportional to the phase gradient. The two major types of artificial structures for generating acoustic OAM,based on diffraction effect and acoustic metasurfaces prescribed with helical phase based on generalized Snell’s law respectively, provides a simple, lowcost and passive alternative to generate acoustic OAM in both 3D and 2D systems with no need of complicated and expensive active arrays or bulky structures with spatially-varying thickness,and have also contributed to manipulate OAM beams to satisfy the needs of different application scenarios, including high-efficiency focusing, realtime splitting, accurate recognition, and so on. With these unprecedented properties offered by acoustic artificial structures which are unattainable in the nature and the unique capability of acoustic OAM beams to transfer torque remotely and information with high-capacity,their combination has shown great potential in many fields such as object manipulation and underwater communication,which may have far-reaching implications in industrial, military and medical science applications.
In this emerging and rapidly growing field, nevertheless,there is still ongoing interest to explore the rich physics underlying the interaction between acoustic vortices and metasurfaces. In particular, despite the discovery of the momentum conservation theory of vortices impinging on metasurfaces with a constant phase gradient, how acoustic vortices will interact with metasurfaces with more complex phase distributions still remains elusive. While acoustic metasurfaces provide a simple, low-cost and passive alternative to conventional OAM production relying on complicated and expensive active phased arrays, there are still challenges in the process of pushing this frontier concept into applications. An inherent limitation of passive artificial structures lies in the fact that the acoustic properties have to be fixed once fabricated, lacking the flexibility of modulating the topological charge,output direction and other parameters of the emitted vortex beam in real time. A feasible solution is to design programmable artificial structures with dynamical OAM-steering functionality,which would greatly promote the vortex-based object manipulation and underwater communication in practice. Yet these important applications still face the difficulties of precise production of vortices with high mode purity by using well-designed artificial structures. Acoustic metasurfaces designed based on the generalized Snell’s law is hard to suppress higher order diffraction when manipulating OAM beams, manifesting the necessity of introducing and engineering the nonlocality in artificial structures to increase the mode purity.[49,57]The underwater environment itself,on the other hand,is also a challenge for the design and implementation of artificial structures for controlling acoustic OAM.The design idea of artificial structures for airborne sound, which is relatively easy due to the innate huge impedance contrast between air and solids, cannot directly apply, and the realization of compact devices for manipulating OAM-carrying waves in water may have to depend on employment of acoustically soft boundaries instead.In addition, the inhomogeneity and instability of real ocean environment,which necessarily lead to effects of beam deformation and path shift which are undesired but virtually impossible to study theoretically, significantly increase the difficulty of vortex detection and recognition. So far these effects have not been taken into consideration in the existing studies of passive artificial structures,while active approaches based on various deep learning algorithms have to be more costly and time-consuming despite the generalization capabilities they provide. In such context, it would be natural to expect an efficient approach by combining passive artificial structures with deep learning algorithms. In particular, one may possibly get new inspirations from other fields such as electromagnetic wave. For instance, the approach of adaptive optics compensation,[77]already found extensive application in optical communication, might open up possibility for design of artificial structures with capability of deformed vortex recognition. Hopefully, the breakthrough in overcoming the above key challenges may gain deeper insight into the vortex-structure interaction and unfold new dimensions to acoustic vortex generation and manipulation by artificial structures with unprecedented merits.
Acknowledgements
Project supported by the National Key Research and Development Program of China(Grant No.2017YFA0303700),the National Natural Science Foundation of China (Grant Nos. 11634006 and 81127901), the Fund from the High-Performance Computing Center of Collaborative Innovation Center of Advanced Microstructures, and the Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Erratum to“Accurate determination of film thickness by low-angle x-ray reflection”
- Anionic redox reaction mechanism in Na-ion batteries
- X-ray phase-sensitive microscope imaging with a grating interferometer: Theory and simulation
- Regulation of the intermittent release of giant unilamellar vesicles under osmotic pressure
- Bioinspired tactile perception platform with information encryption function
- Quantum oscillations in a hexagonal boron nitride-supported single crystalline InSb nanosheet
