基于轨迹跟踪预测的反HTV2 中制导研究*
2022-09-24孙雪琪张锐
孙雪琪,张锐
(1.北京电子工程总体研究所,北京 100854;2.中国航天科工集团第二研究院 研究生院,北京 100854)
0 引言
临近空间高超声速滑翔飞行器(hypersonic technology vehicle 2)HTV2 能够在临近空间实现高速高机动无动力滑翔,实施远距离快速打击。面对这种高速、高机动性目标,拦截弹通常采用复合制导拦截策略。拦截弹需要对目标机动进行稳定跟踪预测,以便拦截弹以最佳的相对几何关系进入末制导[1]。目前国内外对于跟踪临近空间高超声速滑翔飞行器的研究有很多,主要分为基于动力学方程和运动学方程2 类。文献[2]基于目标动力学方程,引入了2 个气动力参数,并使用扩展卡尔曼滤波对该气动参数进行辨识滤波。文献[3]对临近空间高速高机动目标的跟踪算法展开了深入研究,主要针对快速准确的航迹起始和稳定的目标航迹维持来进行展开。文献[4]介绍了几种机动目标跟踪模型和滤波算法,并针对影响跟踪滤波性能的因素进行了分析,引出了自适应跟踪滤波算法研究的必要性。文献[5]提出了一种自适应网格交互多模型算法,该方法能处理自适应时变模型集合,随时调整当前时刻使用的模型数量,并通过数值仿真结果验证了所提算法有效性。
拦截弹使用目标跟踪滤波器可以提取目标机动信息[6],之后利用这些信息对目标轨迹进行预测,获取弹目交会区域,进而计算出拦截弹所要满足的中制导约束[7-8]。目前,针对高超声速滑翔飞行器轨迹预测的主要方法也分为基于动力学和运动学模型两大类。文献[6]基于目标运动学模型,使用最小二乘法对目标弹道角和速度进行多项式拟合,以此预测目标运动状态。文献[9]基于目标动力学模型提出一种多层递阶预测轨迹方法,该方法借鉴多层递阶预测理论对预测模型进行随机补偿,将轨迹预测问题分解成气动参数和模型误差的混合预测以及在此基础上对目标轨迹的预测。文献[10]则针对临近空间高超声速滑翔飞行器机动能力强、轨迹灵活多变的特点,提出了一种基于典型控制规律的高超声速滑翔飞行器轨迹预测方法。
拦截弹通过对目标进行跟踪和预测,获取了目标的运动状态,之后将其用于制导律中,可以补偿目标机动带来的误差。目前常用的制导设计方法有滑模制导律、最优制导律以及改进的比例制导律。例如,文献[6]用扩展卡尔曼滤波估计目标信息,将预测命中时刻目标运动轨迹作为虚拟目标点,采用针对虚拟目标的中制导拦截策略拦截目标。文献[11]针对临近空间防御作战问题,设计了考虑零控拦截的中制导段最优弹道修正算法。文献[12]以导弹逆轨拦截高速运动目标为背景,运用间接高斯伪谱法设计带攻击角度约束的最优中制导律。文献[13]基于导弹和目标相对运动方程,设计了视线角约束自适应滑模中制导律。
本文针对HTV2 目标,提出了一种基于轨迹跟踪预测的反HTV2 中制导算法。使用自适应网格交互多模型(adaptive grid interacting multiple model,AGIMM)滤波器对目标进行跟踪,之后对预测交班点处目标弹道角和速度进行预测,并将其作为中制导约束,通过最优中制导获取满足多约束条件的最优弹道。
1 HTV2 运动特性
要对HTV2 目标进行拦截,需要先对其运动特性进行分析,选取合适的拦截段和拦截策略。HTV2 的运动过程包括主动段、再入段、无动力滑翔段和末制导段。其飞行轨迹灵活多变,横纵向机动性能强。典型的纵向运动有平衡滑翔和跳跃滑翔,横向运动有摆动式和转弯式机动[1]。平衡滑翔是几乎没有起伏的平稳滑翔,此时飞行器在大气层内进行无动力滑翔过程中所受的升力纵平面分量、重力以及离心力达到平衡。只有当选取合适的攻角,使式(1)成立时,飞行器才会进行平衡滑翔运动[2-3]。

式中:L为飞行器所受升力;σ为飞行器的倾侧角;v为速度;m为目标质量;r为目标地心距。
当平衡滑翔条件不满足时,运动轨迹会变为跳跃滑翔。跳跃滑翔的控制量攻角α经常采用常值、分段线性或线性等简单函数来描述,其跳跃幅度呈衰减振荡形式[3]。图1 为攻角取常值时,目标的弹道图。从图中可以看出,此时纵向为跳跃滑翔机动,侧向为转弯机动。
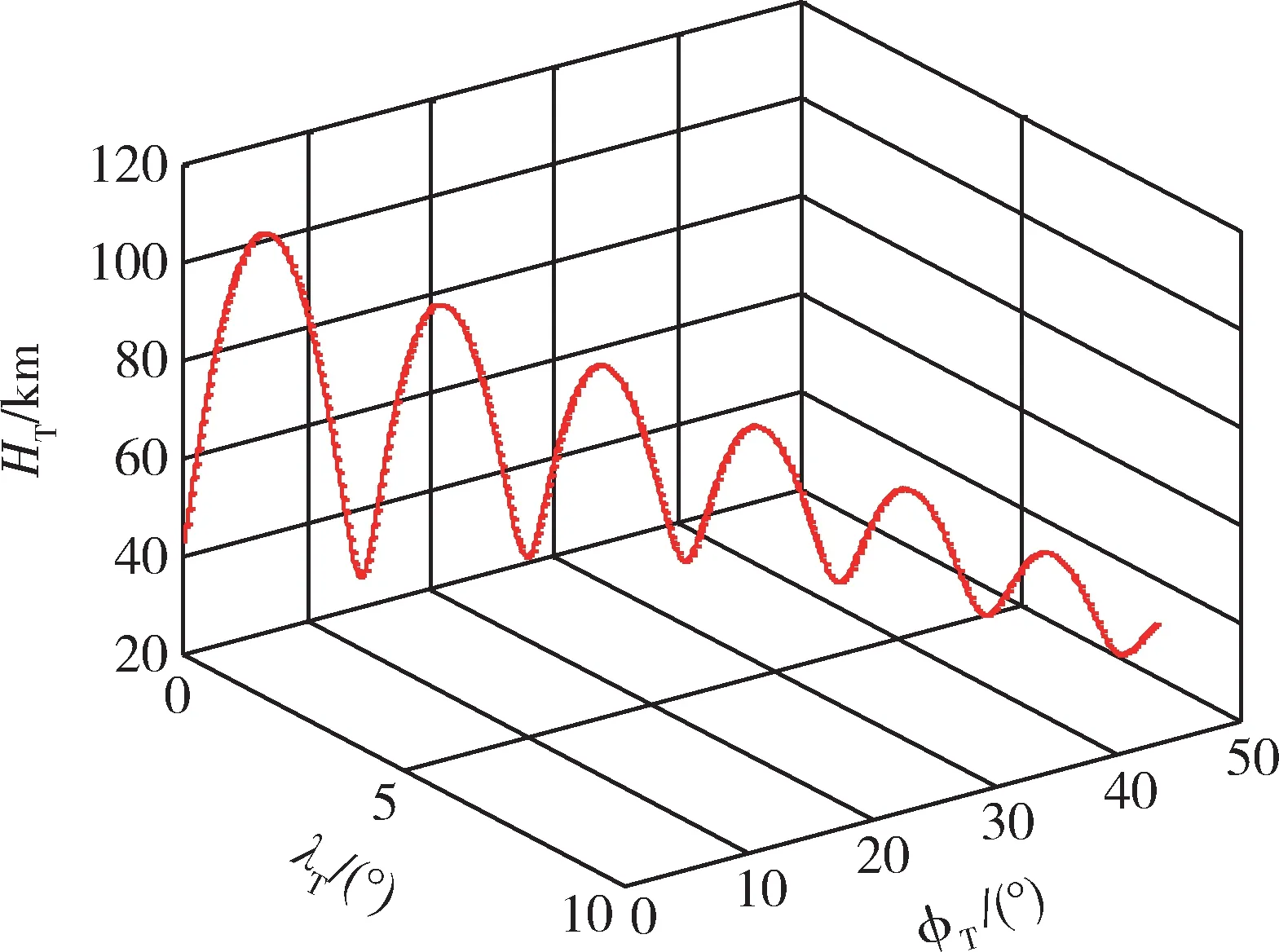
图1 HTV2 常值攻角下的跳跃滑翔弹道Fig.1 HTV2 jump glide trajectory under constant angle of attack
目标侧向机动主要靠倾侧角控制,倾侧角可以改变升力在纵向和侧向上的分量,进而改变飞行器的侧向运动姿态,实现侧向机动突防。典型的侧向机动一般为转弯机动和摆动式机动。侧向最大机动过载为2。图2 为目标进行侧向摆动式机动的弹道。

图2 HTV2 侧向摆动机动弹道图Fig.2 HTV2 lateral swing maneuver trajectory diagram
根据上述分析可知,HTV2 的机动形式多样,机动时机不定,导致目标弹道多变。因此,拦截弹要想成功拦截目标,需要对目标机动进行稳定跟踪和预测,以便根据目标机动做出及时调整。
2 目标跟踪滤波器
2.1 机动模型建立
假设目标做匀转速运动,角速率Ω和速度向量v相互垂直,即=0,因此有

式中:ω为转弯速率。

根据二阶马尔科夫过程,匀转速模型(constant turn,CT)转弯模型可建模为[4]

式中:W为高斯白噪声。

采样时间为T,其离散形式变为

当ω>0 时,运动方程描述向左转弯;当ω<0时,运动方程描述向右转弯;当ω=0 时,模型近似常值速度运动[5-6]。
建立量测方程如下:

式中:Z(k)=ym,ym为目标沿y轴方向的位置量测值;H=(1,0,0);V(k)为量测噪声,设定为零均值白噪声。
2.2 跟踪问题可观性分析
对于如下线性系统:

若满足式(11)条件,则该线性系统是完全可观测的。

故该系统满足条件(11),是完全可观测的。
2.3 AGIMM 跟踪滤波器
目前,AGIMM 滤波器是跟踪高超声速滑翔飞行器最有效的算法之一。相对于传统的模型参数固定的交互式多模型(interacting multiple model,IMM)算法,AGIMM 算法在跟踪过程中能够自适应调整转弯角速率,使得模型集能够随目标机动性的变化实时地调整动态,从而实现对目标的精确跟踪[6]。
AGIMM 滤波器由3 种匀转弯模型组成,分别为向左转弯模型、向右转弯模型和中心转弯模型。其中,中心转弯模型的转弯速率是上一帧3 种模型概率加权和[6],即

式中:ωL(k),ωC(k),ωR(k)为3 种模型的转弯角速率;μL(k),μC(k),μR(k)为3 种模型的模型概率。
模型调整,分为以下3 种情况。
(1)当μC(k)=max{μL(k),μC(k),μR(k)}成 立时,中心模型为最优模型。此时,向左转弯速率调整见式(15),向右转弯速率调整见式(16)。

式 中 :λL(k)=max {ωC(k) -ωL(k),δω};λR(k)=max {ωR(k) -ωC(k),δω},δω为最小网格间距;t1为无效模型的阈值。
(2)当μL(k)=max{μL(k),μC(k),μR(k)}成 立时,向左转弯模型为最优模型。此时,向左转弯速率调整见式(16),向右转弯速率调整见式(17)。

式中:t2为无效模型的阈值。
(3)当μR(k)=max{μL(k),μC(k),μR(k)}成 立时,向右转弯模型为最优模型。此时,向左转弯速率调整见式(18),向右转弯速率调整见式(19)。

通过上述3 种情况对模型进行调整之后,按IMM 算法对目标进行滤波跟踪。AGIMM 算法对初始模型集具有较强的依赖性,需要根据目标的运动特性设置合适的初始参数,提高滤波快速性。
3 目标轨迹预测
目前,针对高超声速滑翔飞行器轨迹预测的方法主要分为基于动力学和运动学模型两大类。基于动力学模型的方法通常先通过跟踪估计出气动参数、升阻比或控制参数的变化趋势,然后研究其变化规律或者借助函数拟合工具给出未来时刻的变化趋势,进而代入动力学模型进行轨迹预测。但是该方法需要通过前期情报搜集和飞行器反设计,对飞行器的本体参数精确已知,并且需要根据飞行器发射位置、光电特性等方面的信息对飞行器进行有效识别[7]。基于运动学模型的方法,首先通过滤波估计目标的运动参数,为预报提供准确的初值。之后,用解析法计算或数值方法迭代获取目标运动轨迹。该方法需要目标的持续跟踪信息,但不需要高超声速滑翔飞行器的先验信息[8-10]。
本文基于目标运动学模型对目标轨迹进行预测,无需获取高超声速滑翔飞行器的先验信息。通过第2 节所给AGIMM 滤波器对目标进行跟踪,可以获取目标的速度信息,之后使用式(20)进行计算,获取目标的弹道角信息。

式中:θT为目标弹道倾角;ψvT为目标弹道偏角;vT为目标速度;vTx,vTy,vTz为目标在发射惯性坐标系下的分速度。
由于目标运动在短时间内具有延展性,据此可以建立目标运动模型,根据目标跟踪结果,使用最小二乘法来计算模型系数[7]。一般情况下,可以将目标弹道角和速度使用多项式进行描述,如式(21)所示。其中,模型系数会随着量测信息的变化而不断更新。

实际上,当目标进行纵向跳跃滑翔时,弹道倾角会呈现出跳跃衰减的变化趋势;当目标进行横向摆动式机动时,弹道偏角会呈现出跳跃变化的趋势。此时,可以建立正弦衰减模型来描述目标的运动状态。如式(22)所示。
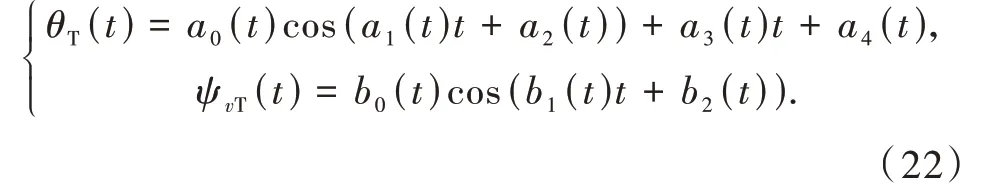
计算得到模型系数后,将预测交班时间代入式(21)或(22),即可获取交班时刻的预测弹道角。其中,交班时间的预测可通过式(23)计算得出。

4 反HTV2 中制导算法
由第1 节的分析可知,HTV2 的典型弹道在纵向平面是跳跃滑翔式的。当地面雷达探测到HTV2后,使用雷达对其进行跟踪,当判断出目标从高点下降后,发射拦截弹对目标进行拦截。初制导段结束后,拦截弹进入中制导段,中制导段包括有动力和无动力段2 个阶段,其中有动力段主要是继续增加导弹速率,并结合弹体的姿态控制,将导弹的速度快速指向需要的方向。在姿态控制阶段结束后,拦截弹进入中制导的无动力阶段。
在纵向平面内,拦截弹在中末交班时刻需要满足侧窗探测视线角约束、视线角速率约束[12],如式(24)~(26)所示。
式中:tf为中末交班时刻;qε为弹目视线倾角;qεd为交班时刻的期望视线倾角;qεmin为侧窗可探测的最小视线倾角;qεmax为侧窗可探测的最大视线倾角;为视线倾角角速率。
此外,拦截弹在中末交班时刻也需要对零控脱靶量进行约束,使其在末制导修偏能力范围之内,保证目标可以被捕获,约束形式如式(27)所示。当交班时刻零控脱靶量为0 时,认为末制导阶段不加控制也能实现对目标的直接碰撞。
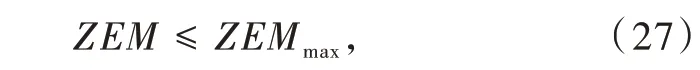
式中:ZEM为中末交班时刻的零控脱靶量;ZEMmax为末制导所能修偏的最大脱靶量。
根据文献[6]中的研究,假设目标不机动,目标和拦截弹的速度比,那么在中末交班过程中拦截弹和目标存在零控拦截条件,且该条件由式(28)唯一确定:
θ(tf)=θd=qεd+arcsin(psin(θT(tf) -qεd)),(28)式中:θ(tf)为交班点处导弹的弹道倾角;θT(tf)为交班点处的目标弹道倾角;p=为交班点处的弹目速度比,可通过第2,3 节轨迹跟踪和预测方法获取。
在侧向平面内,拦截弹同样需要满足交班时刻弹目视线角和视线角速率约束。此外,考虑到末制导阶段采用侧窗探测的方式,拦截弹在中制导段内,需要根据目标机动情况,进行弹道规划,使目标能始终在拦截弹的同一侧,以便为交班时刻导引头捕获目标创造良好的条件。侧向平面约束条件,如式(29)~(31)所示。

式中:qβ为弹目 视线偏 角;qβd为 交班时刻的期望视线偏角;qβmin为侧窗可探测的最小视线偏角;qβmax为侧窗可探测的最大视线偏角为视线偏角角速率。
在纵向平面内,使用最优中制导律可以实现上述多约束条件。首先,建立弹目纵向相对运动方程:

式中:ay为导弹纵向加速度;v为导弹速度,aTy为目标纵向加速度。
对式(32)第2 项求导,则有


设定f=Cδ,其中δ=aTy,由于目标加速度大小是有界的,可推知扰动量f有界。
拦截弹在中末交班时刻期望的状态量x(tf)=(0,0,θd)T,选取性能指标函数如下:

式中:G=,ς为一正数,tj为剩余交班时间;F,Q和G分别表示末端状态量、状态量和控制量的权重系数。
在侧向平面内,使用最优中制导律对视线角和视线角速率进行约束,即可实现中制导策略。令状态量x=(qβ-qβd,)T,x(tf)=(0,0)T。建立如下状态方程:

性能指标函数和参数选取与纵向平面相同。对于该最优控制问题,常用高斯伪谱法来求解最优制导指令[13-16]。图3 为基于轨迹跟踪预测的拦截弹中制导算法流程图。

图3 基于轨迹跟踪预测的拦截弹中制导算法Fig.3 Midcourse guidance algorithm of interceptor missile based on trajectory tracking prediction
5 仿真校验
假设HTV2 采用恒攻角控制,进行纵向跳跃滑翔。拦截弹纵向和侧向均采用上述中制导策略,末制导使用比例导引。仿真开始时刻,目标位置为xT=820 km,yT=40 km,zT=3 km,目标速率为vT=4 500 m/s,目标弹道角为θT=8.78°,ψvT=0°,目标采用恒攻角控制,αT=10°。导弹位置为x=0,y=0,z=0,速度为vx=0,vy=0,vz=0,导引头探测距离为Rj=80 km,拦截弹交班时刻期望视线角为qεd=5°,qβd=0°,侧窗探测范围为qε∈[2°,30°],qβ∈[-4°,4°],零控脱靶量约束参数为ZEMmax=1.2 km。目标在经过65 s 的飞行后,已处于高度下降飞行状态,进入地面雷达的探测范围,此时发射拦截导弹,随后,将此发射时刻记为0 时刻。
5.1 目标跟踪滤波器性能仿真校验
针对上述跳跃滑翔HTV2 目标,分别使用AGIMM 滤波器、基于CT 模型的IMM 滤波器与基于Singer 模型的卡尔曼滤波器(Kalman filter,KF)对目标进行跟踪估计。其中,IMM 滤波器选用和AGIMM滤波器相同的模型集,但是模型集的参数是固定不变的。图4为目标y向加速度估计对比图,图5为目标y向位置跟踪对比图,图6为目标y向速度估计对比图。
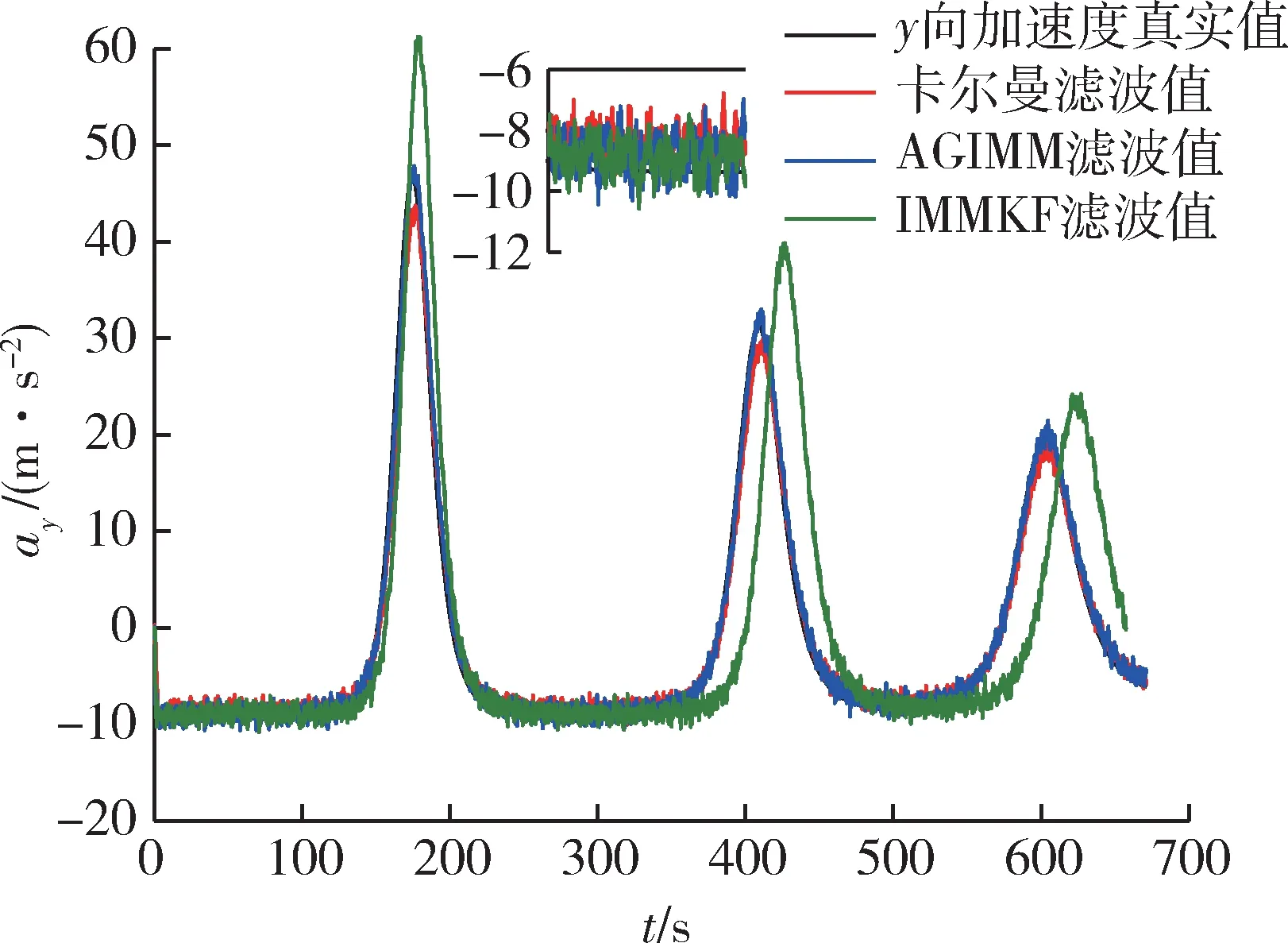
图4 y 向加速度滤波估计Fig.4 y-direction acceleration estimation by filtering
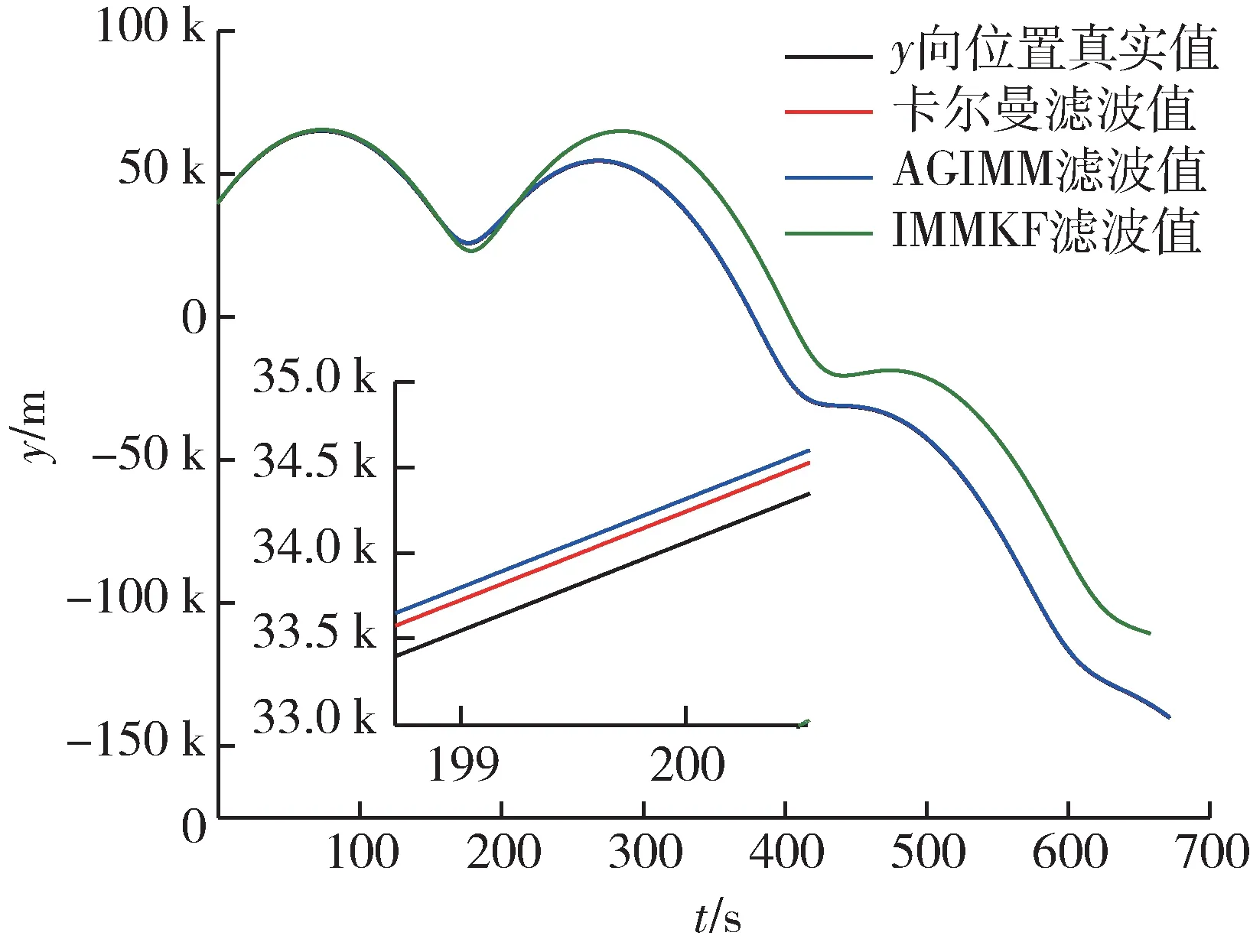
图5 y 向位置滤波跟踪Fig.5 y-direction position estimation by filtering

图6 y 向速度滤波跟踪Fig.6 y-direction velocity estimation by filtering
仿真结果采用均方根误差(root mean square error,RMSE)进行评估,其计算公式为

经过100 次蒙特卡罗仿真,计算出各滤波算法的均方根平均误差如表1 所示。

表1 各滤波算法的RMSE 比较Table 1 RMSE comparison of filtering algorithms
根据仿真图以及表1 可知,相比另外2 种滤波器而言,使用AGIMM 滤波器跟踪该HTV2 目标,所获取的目标信息更接近真实值,具有更高的滤波精度。
5.2 目标轨迹预测仿真校验
当拦截弹进入中制导主动段后,拦截弹开始对目标的弹道角进行预测,之后计算出零控拦截交班所期望的弹道角,将其应用于制导律当中。本文使用最小二乘法对目标进行预测,预测结果与目标真实运动信息的对比图如图7~9 所示。图7 为目标弹道倾角预测值和真实值的对比,图8 为目标弹道偏角预测值和真实值的对比,图9 为目标速度对比图。

图7 目标弹道倾角预测值与真实值对比图Fig.7 Comparison diagram of predicted and real target trajectory

图8 目标弹道偏角预测值与真实值对比图Fig.8 Comparison diagram of predicted and real target trajectory inclination angle

图9 目标速度预测值与真实值对比图Fig.9 Comparison diagram of predicted and real target trajectory deviation angle
从图中可以看出,弹道角和速度的预测值与真实值之间具有相同的变化走向,两者之间的误差如表2 所示。

表2 目标预测值与真实值误差平均值Table 2 Average value of the error between the predicted value and the true value
5.3 反HTV2 中制导算法仿真校验
假设拦截弹交班时刻期望视线角为qεd=5°,qβd=0°,侧窗探测范围为qε∈[2°,30°],qβ∈[-4°,4°],零控脱靶量约束参数为ZEMmax=1.2 km。选取高斯节点数为N=15,性能指标函数权重系数选取Q=15I,F=3I,ζ=20,其中I为单位矩阵。
针对该HTV2 目标,所得拦截弹弹道仿真图如图10 所示。该弹道中末交班时间为79.61 s,交班高度为32.97 km,交班时视线角速率为0.002 4(°)/s,视线角为qεd=0.56°,qβd=-1.69°,零控脱靶量为ZEM=36.20 m。可知交班时刻视线角速率较小,接近于0,视线角在侧窗约束范围内,且零控脱靶量也满足约束。拦截弹在91.28 s 成功拦截到目标,最终脱靶量为0.381 0 m,小于0.5 m,满足直接碰撞拦截的要求。

图10 拦截弹道仿真图Fig.10 Intercept trajectory simulation diagram
对上述算例做100 次蒙特卡罗仿真,结果如图11 所示,统计结果如表3 所示。

图11 蒙特卡罗仿真脱靶量Fig.11 Monte Carlo results of miss distance

表3 100 次蒙特卡罗打靶统计结果Table 3 Monte Carlo shooting statistics
当目标以不同常值攻角跳跃滑翔时,拦截弹拦截弹道簇如图12 所示。此时拦截弹在中制导阶段目标弹道倾角变化如图13 所示。弹道偏角变化如图14 所示。

图12 目标攻角变化时对应拦截弹道簇Fig.12 Intercept ballistic cluster when the target angle of attack changes

图13 目标攻角变化对应拦截弹弹道倾角变化图Fig.13 Interceptor inclination angle diagram when the target angle of attack changes

图14 目标攻角变化对应拦截弹弹道偏角变化图Fig.14 Interceptor deflection angle diagram when the target angle of attack changes
通过第1 节的分析可以得知,HTV2 的机动方式除了在纵向进行跳跃滑翔以外,在侧向也会采用摆动式机动进行突防。当目标分别从高度60 km 开始进行侧向机动,目标倾侧角初始指令正、负皆有,则拦截弹道簇如图15 所示,这些弹道的脱靶量均小于0.5 m,可实现直接碰撞毁伤目标。此时拦截弹对应的弹道倾角变化如图16 所示,弹道偏角变化如图17 所示。
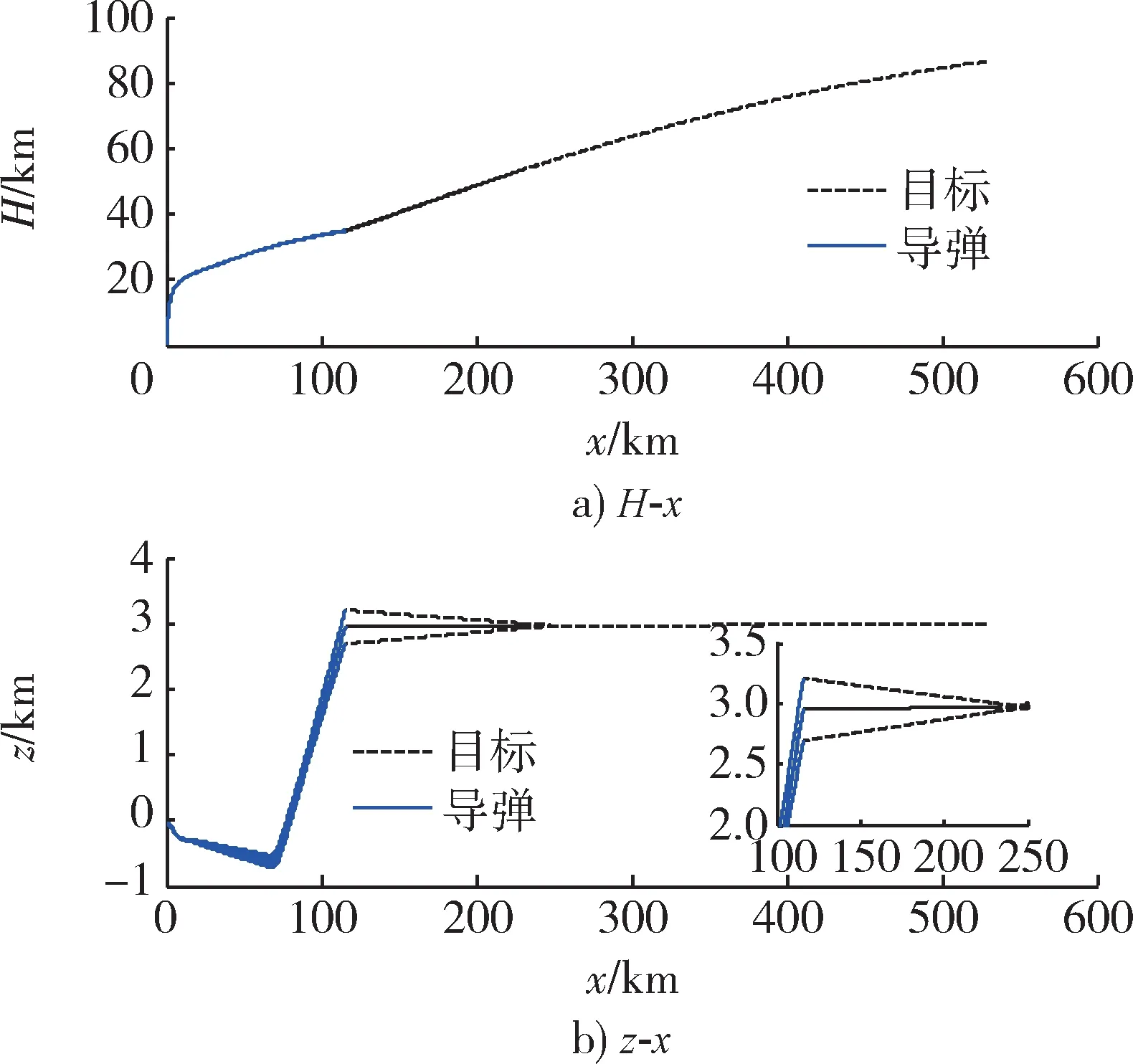
图15 不同侧向机动时机对应拦截弹道簇Fig.15 Different lateral maneuver timing lead to interceptor trajectory cluster
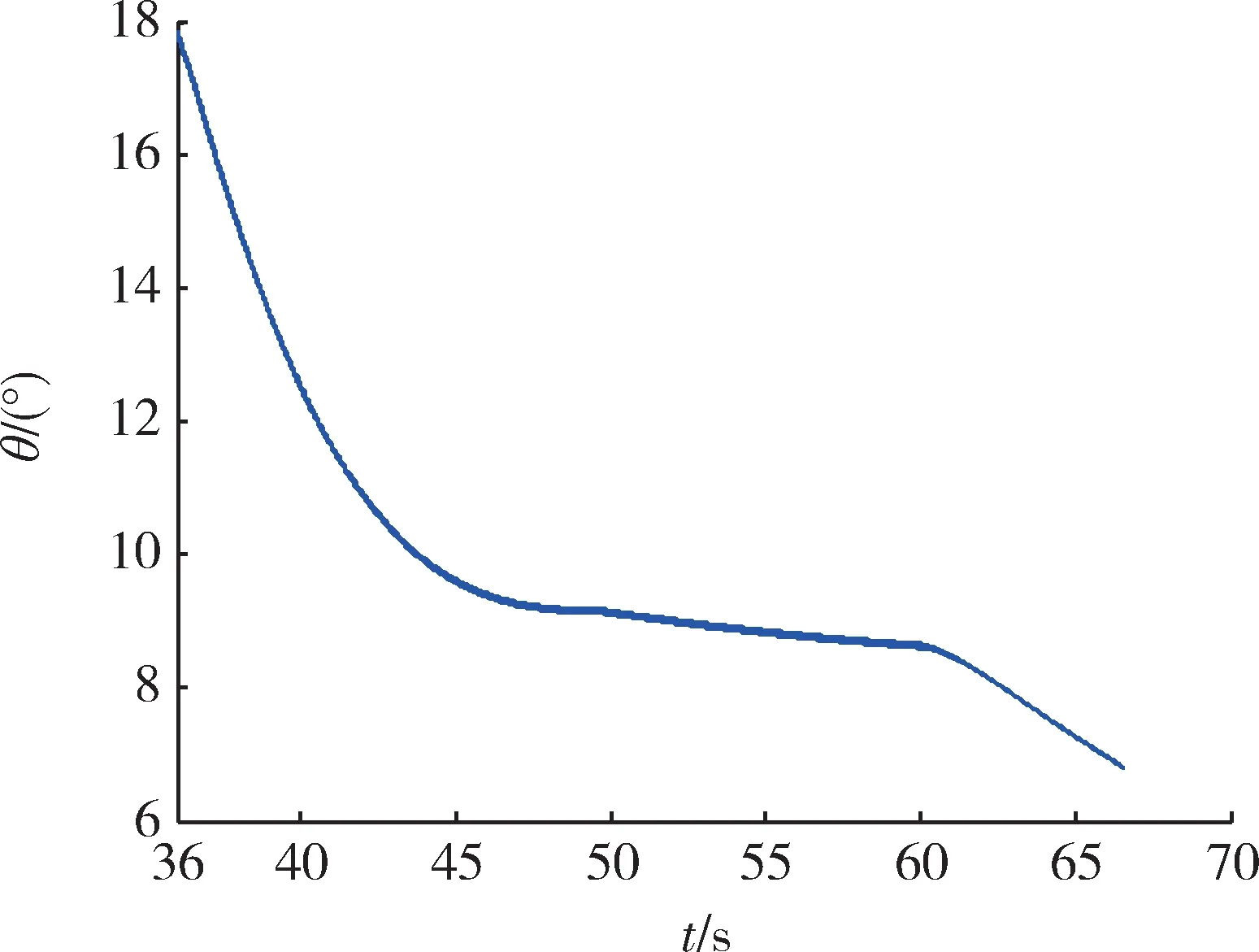
图16 侧向机动时对应拦截弹道倾角变化Fig.16 lateral maneuver lead to the change of the interceptor inclination angle
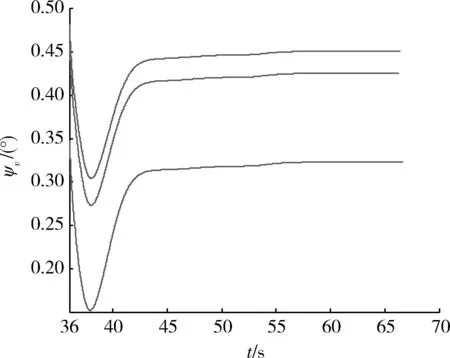
图17 侧向机动时对应拦截弹道偏角变化Fig.17 Lateral maneuver lead to the change of the interceptor deflection angle
通过上述仿真验证可知,本文提出的基于轨迹跟踪预测的反HTV2 中制导算法可以满足中末交班时的视线角、视线角速率和零控拦截弹道角约束。当目标进行机动时,该制导律可以根据目标变化调整弹道角约束,从而满足零控脱靶量要求。
6 结束语
本文针对HTV2 目标,提出了一种基于轨迹跟踪预测的反HTV2 中制导算法。该算法采用AGIMM 滤波器在中制导阶段对HTV2 目标进行跟踪。将滤波结果作为量测值用于轨迹预测中,使用基于遗忘因子的最小二乘法对目标轨迹进行预测,获取中末交班时刻的预测弹道角和速度并用于计算拦截弹中制导约束条件。本文在考虑了视线角、视线角速率、零控拦截等约束条件的基础上,使用最优制导律进行制导。为了验证上述中制导算法的性能,进行了仿真验证。针对给定的目标初始条件,首先进行了目标轨迹跟踪和目标轨迹预测的仿真,之后使用所设计的中制导算法进行拦截弹道仿真。通过仿真结果可知,本文所提基于轨迹跟踪预测的反HTV2 中制导算法可以满足中末交班的视线角、视线角速率和零控拦截弹道角约束,且能够成功拦截不同机动形式下的HTV2 目标。
