乘波体飞行器非脆弱预设性能控制*

卜祥伟，姜宝续

（空军工程大学，a.防空反导学院；b.研究生院，陕西 西安 710051）

0 引言

乘波体飞行器（waverider vehicle，WV）具有高升力、低阻力和高升阻比的突出特点，非常有助于实现其高速飞行。WV 一直以来都是世界各航空航天大国争夺空天权的优先发展方向。控制系统被认为是WV 的“神经中枢”，对于保障其安全飞行和顺利完成任务使命至关重要。WV 特殊的动力学特性给其控制系统设计带来了多重挑战，WV 的飞行控制问题也一直都是控制领域的一个前沿热点问题［1-2］。

近年来，国内外科技人员对WV 的飞行控制进行了系统研究，在模型建立、特性分析与控制仿真等方面取得了丰硕成果［3-5］。文献［5-7］考虑系统受扰、执行器故障、存在约束等情形下WV 的强鲁棒控制问题，虽能保证控制系统满意的稳态精度，但对误差收敛过程的瞬态性能无法进行定量或定性设计。鉴于WV 大机动飞行对其飞行控制系统的动态性能有着极高的要求，在保证控制系统稳态性能的基础上，还必须确保其具有出色的动态性能［8］。预设性 能 控制［9］（prescribed performance control，PPC）已被证明是一种可以有效保证控制系统满意动态性能的新方法，近年来在WV 的飞行控制中也有较多创新性研究。针对传统PPC 依赖精确误差初值的技术缺陷，文献［10］通过设计一种新型性能函数，为WV 提出了一种新颖的神经网络PPC 方法。仿真结果虽然证明了该算法的有效性，但是过大的性能函数初值有可能导致跟踪误差的超调量失控。为此，文献［11］提出了一种可以保证跟踪误差小超调（甚至零超调）收敛的PPC 新方法，并将其应用于WV 的飞行控制，保证了速度跟踪误差与高度跟踪误差零超调收敛。进一步，文献［12］针对传统PPC［9-11］收敛时间不明确的缺点，构造了一种有限时间收敛的新型性能函数，可以保证跟踪误差在任意设定的时间内收敛到稳态，进一步提高了PPC 方法的工程实用性。

尽管现有WV 的PPC 研究也取得了一定的进展，但同时应当看到，现有研究还存在明显不足。上述PPC［9-12］方法为了保证控制鲁棒性，通常采用神经网络或者模糊系统对WV 的未知模型进行在线逼近，并基于Lyapunov 理论为权值向量设计使闭环系统渐近稳定的在线学习律，这必然导致过大的在线学习量［13］，难以保证WV 机动飞行对其控制实时性的苛刻要求。此外，WV 在临近空间飞行时遭受的外部突变扰动必然会引起跟踪误差的短时间波动，如果误差波动幅度过大，就会造成误差接近甚至越过PPC 的约束包络，将直接导致控制奇异，此亦即所谓的现有PPC 的脆弱性缺陷［14］。

基于以上分析，本文为WV 提出一种无需任何在线学习参数的非脆弱PPC 新方法。通过设计一种新型性能函数，使得PPC 的约束包络能够自主“感知”误差波动情况，并有针对性地调整约束包络的形状，从而避免传统PPC 可能存在的控制奇异问题，并克服现有PPC 的脆弱性缺陷。基于Lyapunov理论证明了闭环控制系统的稳定性以及预设性能的可达性。最后，通过数值对比仿真验证了所提方法的有效性和优越性。

1 WV 运动模型

美国学者Bolender［3］等将WV 机体横向宽度单位化，建立了纵向运动的一体化解析式二维模型，为飞行控制设计提供了模型基础。Parker［4］等进一步将该模型进行合理简化，建立了如下被广泛采用的参数拟合模型：

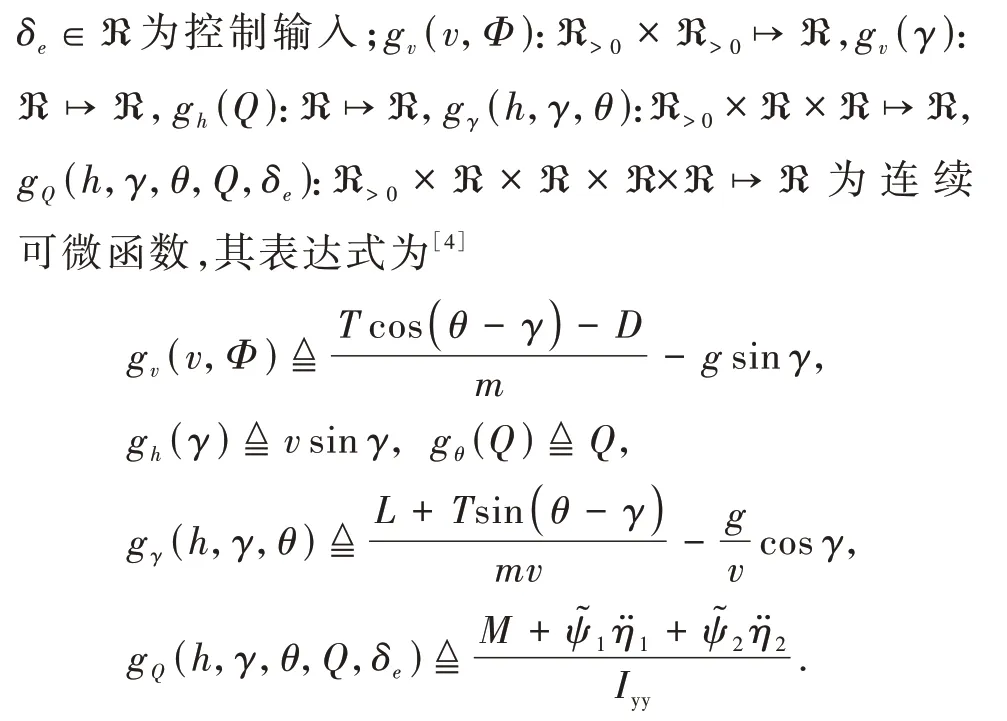
注释1：WV 的几何外形与受力情况如图1 所示。WV 的纵向运动模型包含5 个刚体状态、2 个弹性状态和2 个控制输入。参数与变量详细定义见表1。由于弹性状态η1与η2完全不可测，借鉴相关文献［6，8，15］的通常做法，将利用控制系统的鲁棒性对弹性振动进行被动抑制。

表1 参数定义Table 1 Definitions of parameters

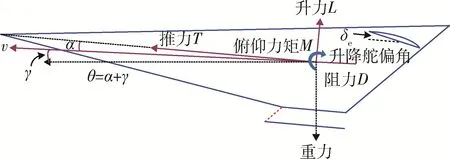
图1 WV 几何外形与受力示意图Fig.1 Geometry and force map of WVs

控制目标是：为Φ，δe设计合适的控制律，使得v→vr，h→hr，γ→γr，θ→θr，Q→Qr，并且所有跟踪误差均满足期望的非脆弱预设性能。这里，vr∈ℜ＞0，hr∈ℜ＞0为给定的参考指令，γr∈ℜ，θr∈ℜ，Qr∈ℜ 为待设计的虚拟控制律。

假设1［15］：vr∈ℜ＞0，hr∈ℜ＞0及其对时间的一阶导数∈ℜ＞0，∈ℜ＞0均有界。

2 非脆弱PPC 设计

传统PPC 在遭遇强干扰时，极易诱发控制奇异，表现出明显的脆弱性缺陷。为此，将为WV 的速度子系统（即式（1））与高度子系统（即式（2）～（5））设计一种新型非脆弱PPC 策略。

2.1 速度控制律设计

设计目标是为Φ选取合适的控制律，使得跟踪误差=v-vr满足如下非脆弱预设性能

考虑到不等式（8）不便于控制器设计，对其进行如下等价变换

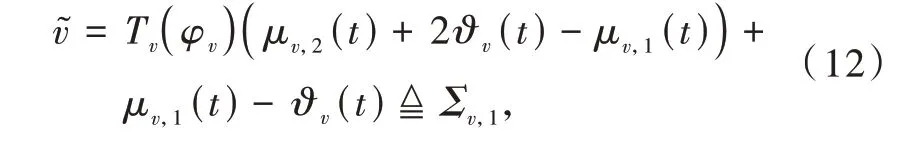
式中：Tv(φv)=exp(φv)/(1+exp(φv))为转换函数；φv∈ℜ 为转换误差。由于Tv(φv) ∈(0，1)，则易知式（12）与式（8）等价。

对式（12）求逆，得到

将速度控制律Φ设计为

式中：ιv∈ℜ＞0。

下面，对速度子系统的稳定性进行证明。

对式（13）求导并代入式（1），（12），可得

式中：κv∈(0，1)。

将式（16）代入式（15），可得

2.2 高度控制律设计

注释3：与ϑv(t)具有类似功能，ϑi(t)，i=h，γ，θ，Q能够根据误差波动情况自主调整约束包络（20），以确保跟踪误差始终位于约束包络内，并克服传统PPC 的脆弱性缺陷。

鉴于不等式（20）不便于控制器设计，对其进行如下等价变换

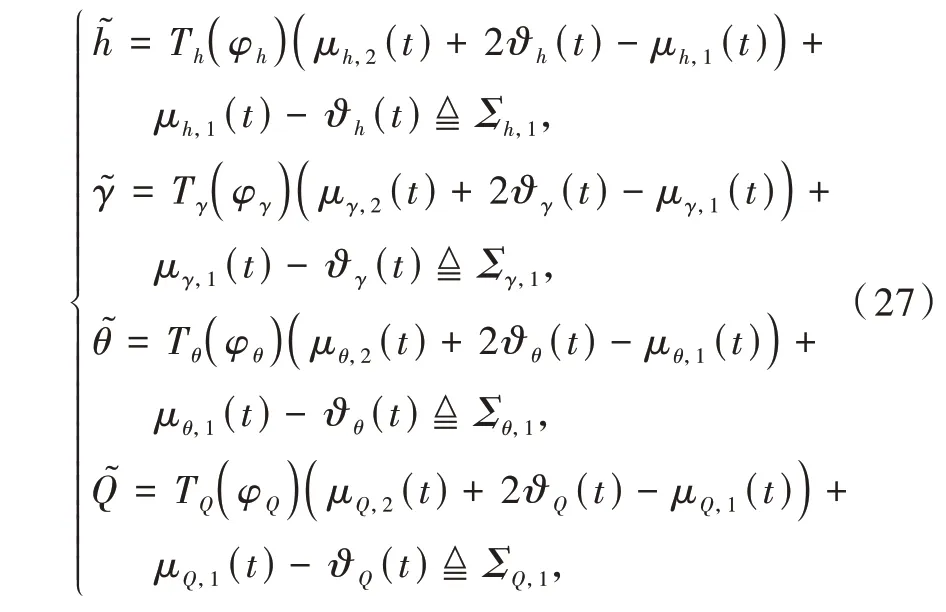
式中：Ti(φi)=exp(φi)/(1+exp(φi))为转换函数，φi∈ℜ为转换误差，i=h，γ，θ，Q。由 于Ti(φi) ∈(0，1)，i=h，γ，θ，Q，则易知式（20）与式（27）等价。

对式（27）求逆，得到

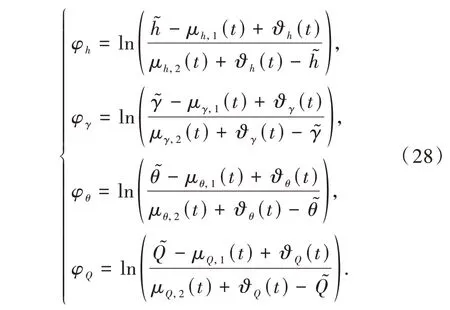
将虚拟控制律γr，θr，Qr以及高度控制律δe分别设计为

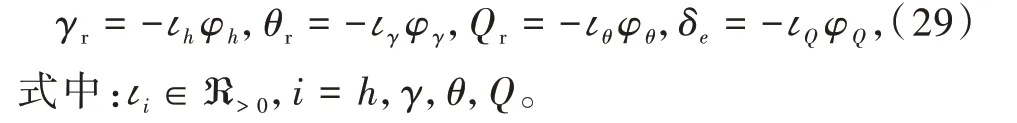
下面，对高度子系统的稳定性进行证明。

对式（28）求导并代入式（3）～（5），（27），可得

对式（36）求导并代入式（28）与式（35），可得

注释3：传统反演控制方法［15］需要精确获知虚拟控制律的一阶导数，存在所谓的“微分项膨胀”问题。本文所设计的控制律（14），（29）不仅构型简单，而且不需要虚拟控制律的导数，避免了传统反演的“微分项膨胀”难题。

注释4：传统PPC 方法［9-13］在遭受强突变干扰时极易造成控制奇异，表现出明显的脆弱性缺陷。本文所设计的新型约束包络（8），（20）饱和修正项ϑi(t)，i=v，h，γ，θ，Q，能够自主“感知”误差波动并自动调整约束包络，从而弥补了现有PPC 方法［9-13］的脆弱性缺陷。

3 数值仿真验证

为了验证本文所设计控制律（14），（29）的有效性以及相对于现有方法［9］的优越性，以式（1）～（7）作为被控对象，采用Matlab/Simulink 软件进行数值对比仿真。仿真采用四阶龙格-库塔法进行解算，仿真步长为0.01 s。控制增益参数取为：ιv=0.3，ιh=0.04，ιγ=0.05，ιθ=0.1，ιQ=0.5。速度跟踪 误差约束包络的设计参数取为：μv0=5，μvf=0.9，av=2，bv，2=15，bv，1=0.5，Tf，v=3。高度跟踪误差约束包络的设计参数取为：μh0=1.5，μhf=0.5，ah=2，bh，2=5，bh，1=2，Tf，h=3。航迹角跟踪误差约束包络的设计参数取为：μγ0=0.1，μγf=0.02，aγ=2，bγ，2=5，bγ，1=5π/180，Tf，γ=3。俯仰角跟踪误差约束包络的设计参数取为：μθ0=0.1，μθf=0.01，aθ=2，bθ，2=4，bθ，1=π/180，Tθ，h=3。航迹角速率跟踪误差约束包络的设计参数取为：μQ0=0.2，μQf=0.03，aQ=2，bQ，2=5，bQ，1=π/180，TQ，h=3。

仿真过程中，考虑系统同时存在参数摄动和外部扰动。假定系统参数随时间摄动±35%（变化规律为sin(0.1πt)）。并考虑如下外部扰动：

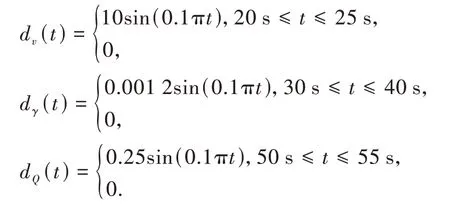
仿真1：采用本文所提出的非脆弱PPC 方法进行仿真。仿真结果如图2～10 所示。

由图2，4 可见，当系统存在参数摄动与外部扰动时，本文所提方法仍能实现速度与高度对各自参考指令的稳定跟踪。由图3，5～8 可见，所有跟踪误差均被限定在预设的约束包络内，从而满足期望的动态性能与稳态精度。尤其是图3 表明，当速度跟踪误差因为外部扰动而增加并逐渐靠近约束包络时，本文所提方法的约束包络能够自动“感知”误差的这种变换趋势，并自主调整约束包络（增大上包络，减小下包络），从而避免了传统PPC 可能存在的控制奇异问题。图9，10 表明，速度控制输入与高度控制输入能够动态地响应系统参数摄动和外部扰动，保证了控制鲁棒性。

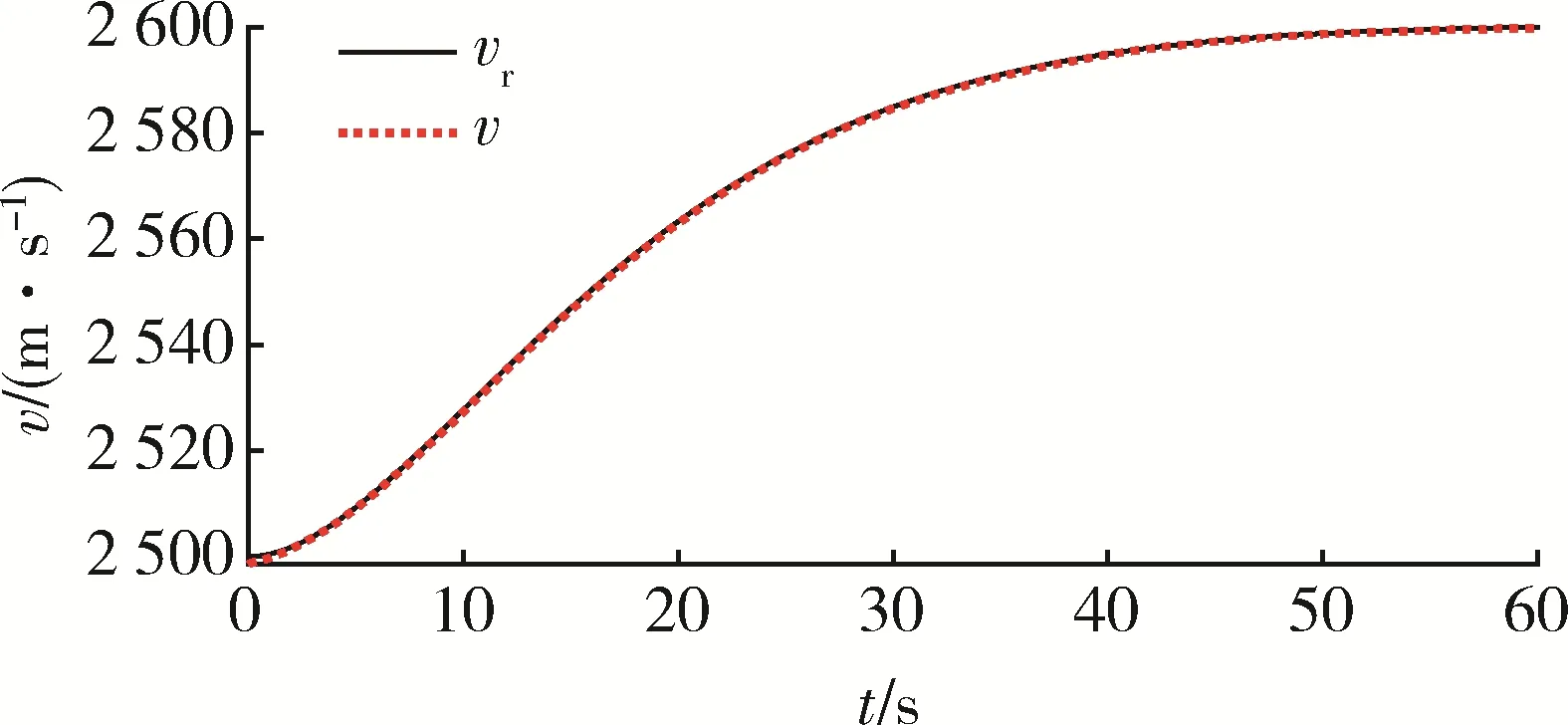
图2 所提方法的速度跟踪效果Fig.2 Velocity tracking performance of the proposed method

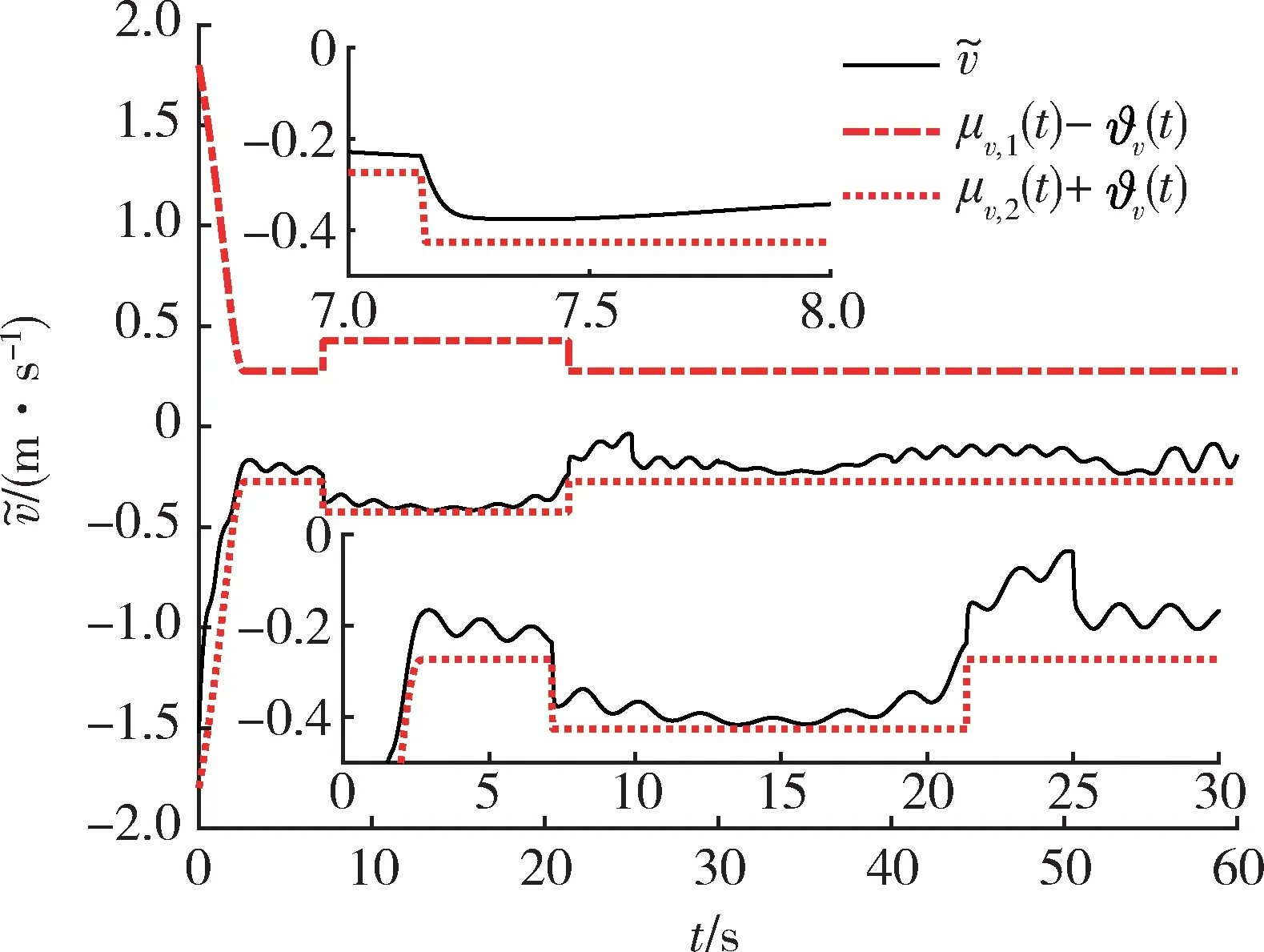
图3 所提方法的速度跟踪误差Fig.3 Velocity tracking error of the proposed method

图4 所提方法的高度跟踪效果Fig.4 Altitude tracking performance of the proposed method

图5 所提方法的高度跟踪误差Fig.5 Altitude tracking error of the proposed method

图6 所提方法的航迹角跟踪误差Fig.6 Flight-path angle tracking error of the proposed method

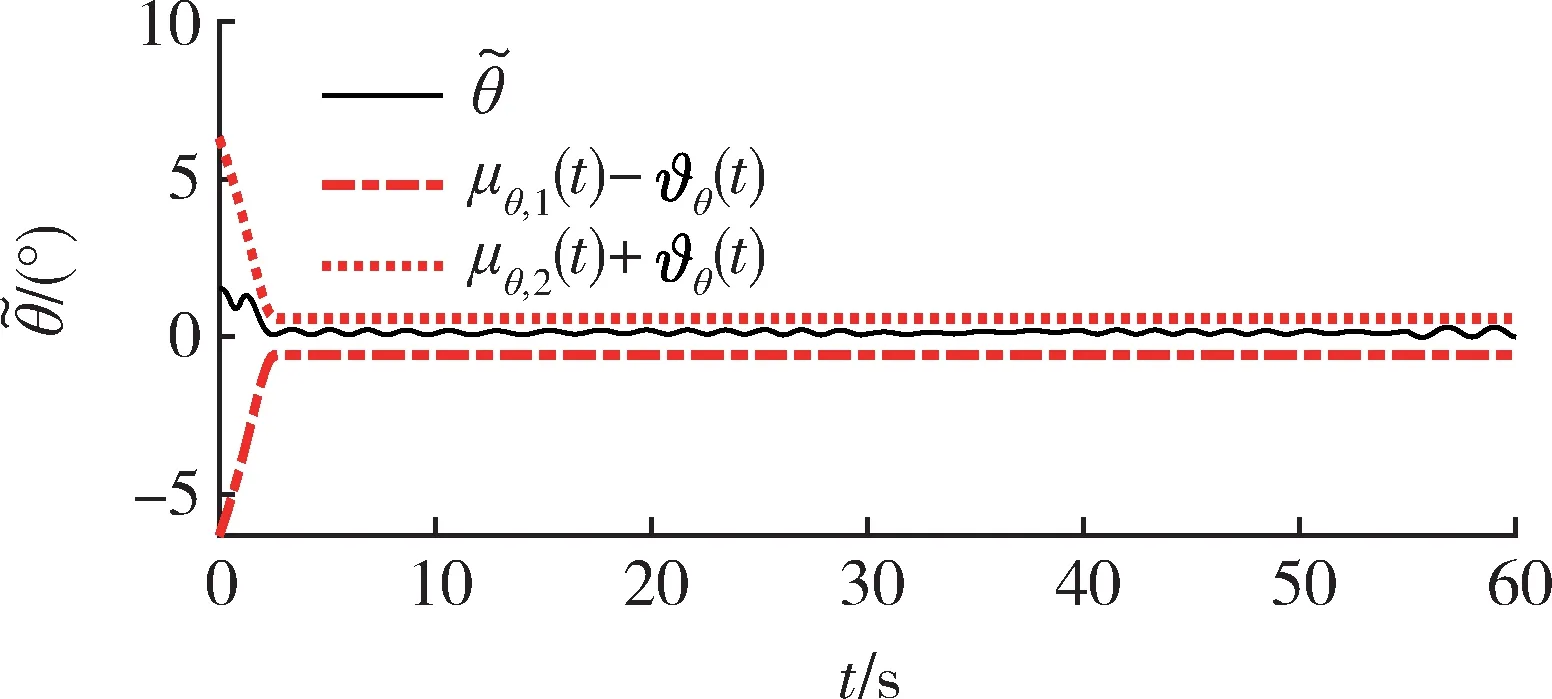
图7 所提方法的俯仰角跟踪误差Fig.7 Pitch angle tracking error of the proposed method

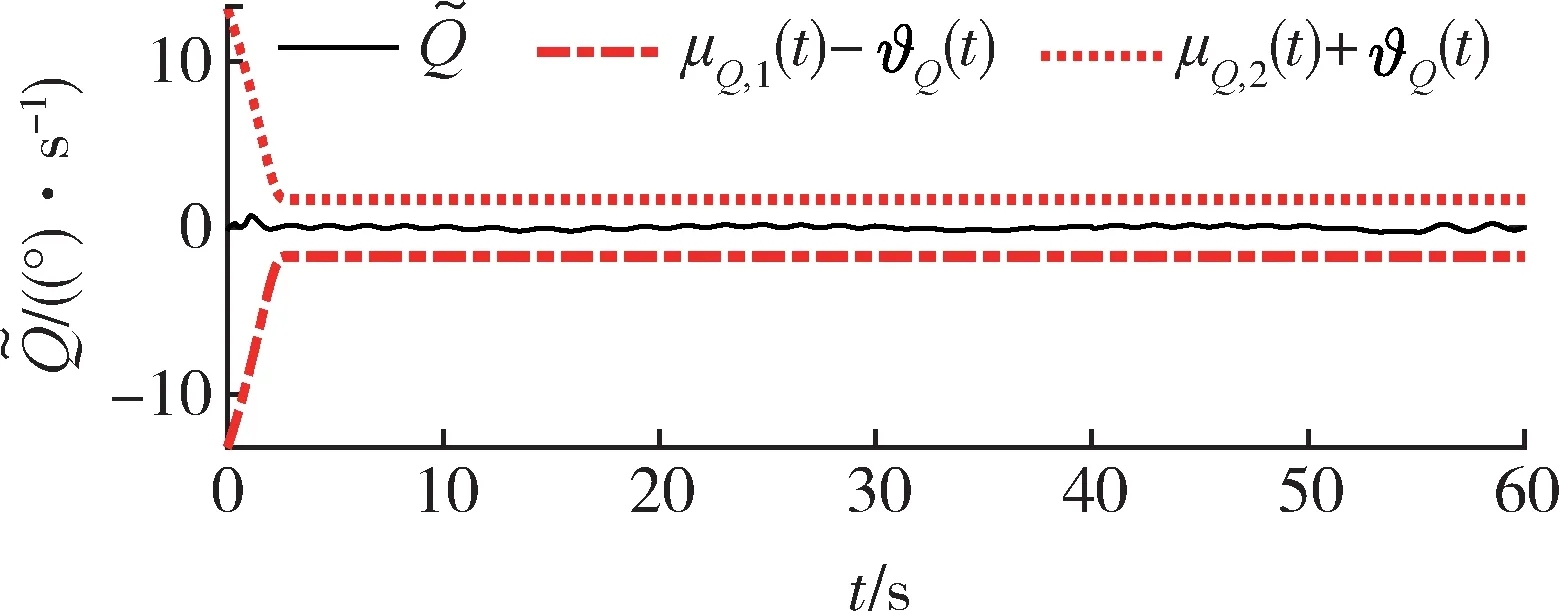
图8 所提方法的俯仰角速率跟踪误差Fig.8 Pitch rate tracking error of the proposed method

图9 所提方法的速度控制输入Fig.9 Velocity control input of the proposed method

仿真2：在与仿真1 同等条件下，采用文献［9］的传统PPC 方法。仿真结果如图11～15 所示。

图12～15 表明，当采用文献［9］的传统PPC 方法时，虽然也能将高度跟踪误差、航迹角跟踪误差、俯仰角跟踪误差以及俯仰角速率跟踪误差限定在约束包络内，但是由图11 可见，当外部扰动导致速度跟踪误差增加时，文献［9］的传统PPC 方法不具备约束包络的再调整能力，导致速度跟踪误差越过了约束包络，将直接造成控制奇异。综上所述，数值仿真结果充分验证了所提方法的有效性以及相对于现有方法的优势。

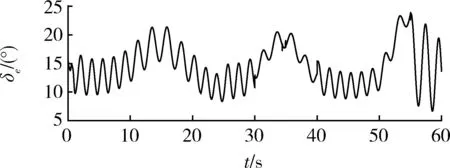
图10 所提方法的高度控制输入Fig.10 Altitude control input of the proposed method

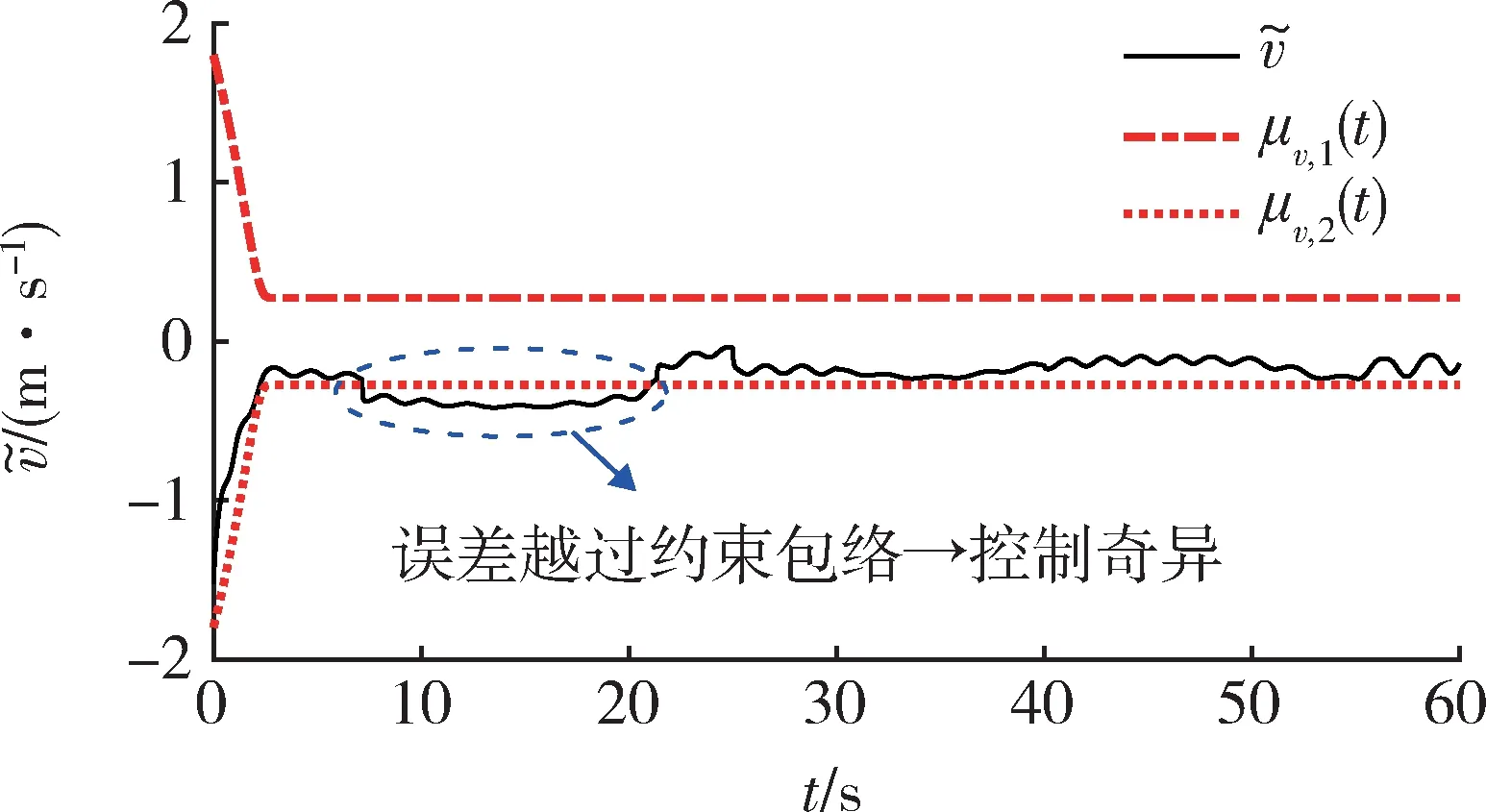
图11 文献［9］方法的速度跟踪误差Fig.11 Velocity tracking error of the method in［9］

图12 文献［9］方法的高度跟踪误差Fig.12 Altitude tracking error of the method in［9］

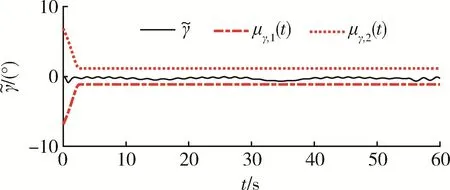
图13 文献［9］方法的航迹角跟踪误差Fig.13 Flight-path angle tracking error of the method in［9］

图14 文献［9］方法的俯仰角跟踪误差Fig.14 Pitch angle tracking error of the method in［9］

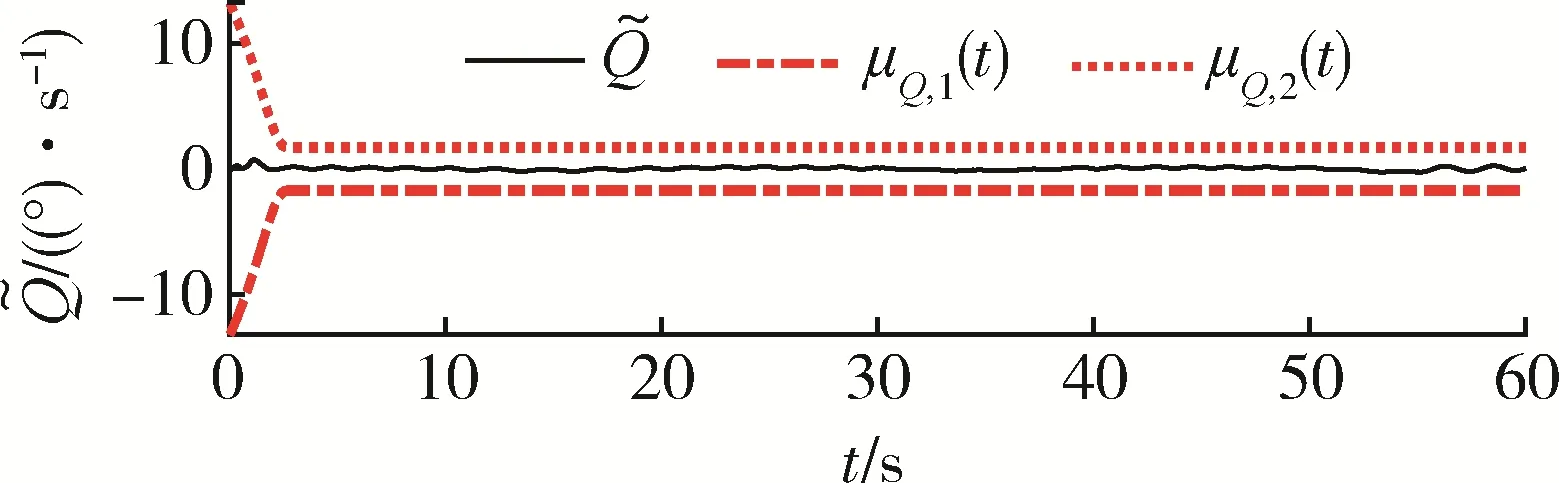
图15 文献［9］方法的俯仰角速率跟踪误差Fig.15 Pitch rate tracking error of the method in［9］

4 结束语

本文针对WV 受扰条件下的跟踪控制问题，提出了非脆弱PPC 新方法。为了克服传统PPC 的脆弱性缺陷，设计了1 种新型性能函数。所构造的约束包络能够根据由误差引起的误差波动情况，自适应地调整包络形状，从而避免了控制奇异问题。稳定性分析表明，当存在外部扰动时，仍能保证所有跟踪误差期望的预设性能。不同于传统基于神经/模糊逼近的PPC 方法，本文所提方法无需任何在线学习参数，且能避免传统PPC 的脆弱性缺点。对比仿真结果证明了所提方法相对于现有方法的优越性。