梁格法求转体曲线桥预偏心的方法研究

薛 达

（广东省铁路规划设计研究院有限公司，广东 广州 510000）

0 引言

随着我国基础设施建设和城镇化的大力发展，出现了很多桥梁上跨铁路或重要公路的情况，往往桥梁转体成为首选方案。与传统施工工艺相比，转体施工工艺具有不干扰交通、不间断通航、可跨深沟、河流、交通频繁的道路的特点，同时也具有施工快速、经济高效、对既有线运营安全威胁小等优点，被越来越广泛地采用。而由于地形、征地拆迁或既有交通设施的影响，在某些情况下不得不采用曲线桥转体跨越。对于曲线桥转体，球铰预偏心准确设置是转体成功的重要因素之一。

陈爱荣[3]阐述了大跨径小半径曲线桥梁转体结构的设计要点和设置恒载横向偏心的处理方法，但并未讲述横向偏心计算方法。田山坡[4]对小半径曲线转体桥调偏心进行研究，讲述上转盘永久配重、临时配重技术等施工方法。王博妮[5]对小曲线半径转体桥梁不平衡力矩进行研究，提出构造纠偏、桥面配载、不平衡力矩称重等方法，主要研究纠偏措施。曾明辉[6]提出用最小扭转应变能设置连续弯梁桥支座预偏心，理论抽象，工程设计普遍性不强，且研究对象不是曲线桥转体。鲍志旺等[7]采用ANSYS实体建模，对独柱小半径匝道弯桥的预偏心设置进行分析。郑超等[8]建立单梁和梁格模型，对小半径连续弯箱梁桥的支座预偏心设置进行分析对比，发现单梁法得到的支座反力与实际受力状态不符，而用梁格法得到的结果与实际情况较接近，但都是定性的分析，缺少对梁格法解与准确解的误差比较。

与预偏心计算有关的文献多以连续弯梁桥为研究对象，而与转体有关的文献均未讲述预偏心如何准确计算，相比常规曲线桥，转体曲线桥的预偏心精度要求更高。若用单梁法，工程精度得不到保证，而用实体建模时间则较久，复杂桥梁建实体有可能布尔操作失败。用梁格法是可行的方法，且市面上多数桥梁专业软件均有快速建立单梁建立梁格模型的功能模块，能够满足设计效率，但对于不同曲线半径、桥宽、桥长的转体结构，梁格法是否均适用，以及需划分几片子纵梁才能满足转体曲线桥精度要求，未有类似研究的文献。

本文以东莞塘厦镇环市南路上跨广深铁路2×68 m转体桥梁为背景，对梁格法求转体曲线桥预偏心进行研究，可对转体曲线桥的预偏心准确设置提供指导作用。

1 工程概况

环市南路上跨广深铁路工程位于东莞市塘厦镇,由于广深铁路繁忙，且工程附近存在密集房屋，受多个客观因素制约，上跨桥梁位于半径400 m的曲线上，采用2×68 m预应力混凝土T构逆时针转体70.5°跨越广深铁路四股道以及塘天中路，转体重量约15 000 t。桥宽25.5~29.55 m，采用单箱三室斜腹板箱形截面，中支点中心梁高6.5 m，端部中心梁高3.0 m，梁底线形按1.8次抛物线变化。顶板宽29.55 m，底板宽度为19.525 m。箱梁两侧悬臂板长3.5 m，悬臂板端部厚20 cm，根部厚60 cm。悬臂板与外腹板加腋处采用半径R=0.2 m圆弧过渡。主桥采用墩梁固结，桥墩高9.0 m，设上下承台，承台下设置24根1.8 m钻孔灌注桩。桥型布置图、转体墩处横断面见图1、图2。

图1 桥型布置图

图2 转体墩处横断面图

本项目的结构特点：空间关系复杂,主梁平面曲线半径小、顶板单向横坡、内外斜腹板不等高、变梁高和变腹板厚等。若建立实体模型求预偏心不仅难度很大且花费时间久，往往没有充足的设计时间，而预偏心的准确设置对桥梁的成功转体至关重要。

2 单梁法求曲线桥预偏心的弊端

单梁法是应用最广泛的有限元计算方法，其计算的内力、变形等在多数时候均能满足工程精度需求，但对于小半径曲线转体桥梁，预偏心的偏差较大，其根本原因是现行的杆系有限元软件，均是以直代曲来进行力学求解，如图3所示。由于内移区、重叠区和外空区1、2的影响，截面重心较实际重心有所内移，曲线半径越小内移越多。对于外空区1和内移区的影响可通过减小单元长度来减小，而对于重叠区和外空区2，减小单元长度只是将重叠区面积匀给其他单元，无法消除重叠区的影响。

图3 单梁模型以直代曲示意图

3 矩形等截面转体曲线桥

由于箱梁截面可近似看作外矩形减内矩形，故箱梁与矩形梁可能有类似的规律，因此先从矩形截面梁入手,进行梁格法求预偏心的方法研究，对箱梁结构有一定指导意义。研究思路为先进行预偏心理论公式推导，再进行梁格模型计算，最后对梁格结果与理论值进行对比，分析误差找出规律。

3.1 预偏心理论公式推导

假设矩形截面曲梁的外径为R，内径为r，单位梁高，建立平面极坐标系ρ-θ，如图4，微元体的面积为ρ·dρ·dθ，到A-A轴的距离为ρ·cosθ。偏心距的公式推导如下：

图4 矩形曲梁偏心距公式推导图

到A-A轴的面积矩：

曲梁平面面积:

曲梁形心到A-A轴的距离:

曲梁形心到B-B轴的距离:

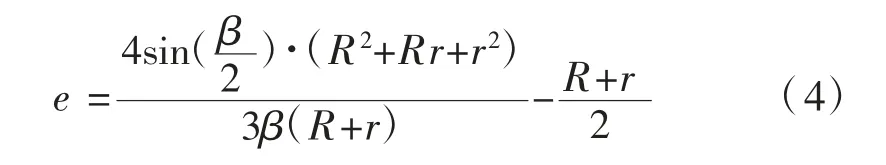
曲梁支反力F、反力矩M：

3.2 梁格模型的参数选取

为保证规律研究的通用性，梁格模型尽量包括工程上可能遇到的曲线半径、桥长、桥宽等情况。曲线半径根据《公路路线设计规范》（JTG D20—2017）表7.3.2 确定，可以看出曲线半径在15~1 000 m，详见表1。转体单侧悬臂长取30~100 m，桥宽取5~50 m，梁格划分子纵梁片数取2~50 片。梁格参数见表2，共需建立3 840 个梁格模型。

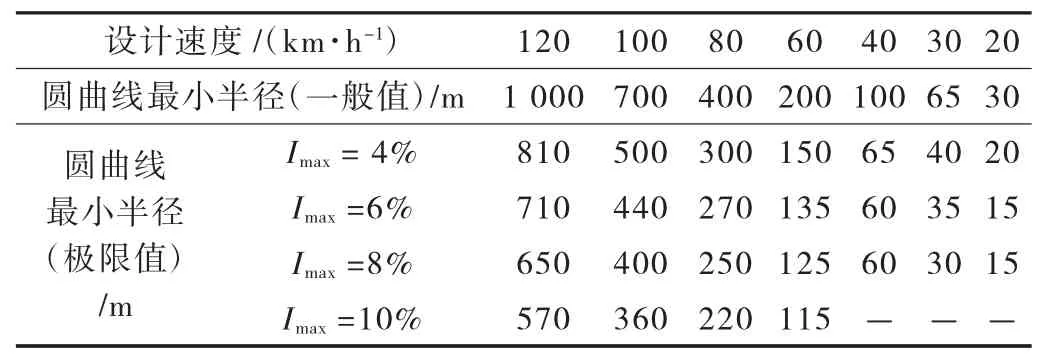
表1 《公路路线设计规范》圆曲线最小半径表

表2 各梁格模型参数表

由于模型数量庞大，故采用ANSYS 的APDL 参数化编程语言进行编程计算。具体方法如下：首先通过4 层循环嵌套将表2 的参数进行一一组合，得到3 840 行×4 列的二维数组,即每个梁格模型的参数；然后编写基于表2 中4 个参数的梁格模型宏命令；最后写循环调用语句，逐行调取二维数组的数据进行梁格计算，得到支反力结果。

表2 可以看出存在桥宽大于曲线半径的情况，显然不符合实际，故编程中添加了判断语句进行剔除，最终有效模型数为3 600 个。

由于研究的是曲梁，故梁格单元采用BEAM189单元，该单元为3D 二次有限应变梁单元，可很好地模拟曲线梁。图5 为2、10、50 片子纵梁的梁格模型。

图5 梁格模型图

3.3 梁格模型计算结果分析

将梁格模型的反力与理论值进行比较，误差对比如图6 所示，反力误差在0.000 02%，与理论反力值几乎相等，而部分模型的反力矩误差较大（最大达5 237%），且误差较大的多为2 片子纵梁的模型。可见稀疏梁格的误差较大，现对划分子纵梁片数与预偏心误差的关系进行研究，关系图示于图7。

图6 梁格模型的支反力结果与理论值的误差比较图

由图7 可以看出以下规律：

图7 预偏心误差与划分子纵梁片数的关系图

（1）当为稀疏梁格，预偏心误差值分布发散，有些模型误差最大，有些模型误差较小。

（2）子纵梁片数的增加可以极快地减小误差值，说明只要适当地划分就可得到很好的误差收敛效果。

（3）当达到致密梁格时，误差均趋于0，即等于理论值。

3.4 求预偏心的推荐方法——梁格收敛法

通过3.3 节分析，说明用梁格法求预偏心是可行的，但子纵梁的合理划分片数却不能得到确切的答案，划分太疏无法满足工程要求，划分太密则带来时间成本的开销。显然准确算出预偏心的代价太大，工程上常采用配重来调整转体桥的偏心值，因此只要得到满足工程精度要求的预偏心值即可。如图8 所示，只要能证明梁格求得的预偏心值与精确值的误差小于配重可调值δ，则该预偏心值即可满足工程要求。

图8 梁格收敛曲线分析图

由图7可以看出，梁格误差收敛曲线与指数曲线y=kax，（0＜a＜1，k＞0）相似，采用指数曲线对误差最大的梁格收敛曲线进行拟合，如图9所示，可以看出拟合较好，对应的指数方程为y=3.8×0.67x。

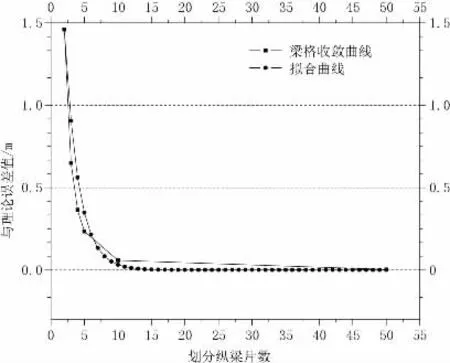
图9 指数函数拟合曲线

鉴于梁格误差曲线的收敛性，引入δ与有关的参数δ/n（δ为配重可调值，n为待求的调整系数）作为收敛标准,假设子纵梁片数为m时开始满足收敛标准δ/n，即满足公式kam-kam+j=kam（1-aj）≤δ/n，经化简，得kam≤δ/[n（1-aj）]，显然只有n（1-aj）≥1，预偏心才能满足kam≤δ，即梁格预偏心值与精确值的误差kam小于δ配重可调值。

因n、a值的准确确定是困难的，为得到普遍性规律，基于统计学思想，对图7的所有曲线（即第3.2节所述的3 600个模型）进行aj和n值计算，见图10。由于配重可调值δ一般为0.02~0.1 m，故可剔除初始值小于0.02 m的曲线，可以看出，aj值范围为0.018~0.796，n值范围为1.02~4.90，可以看出初始误差越小n值离散性越大，而初始误差大时，n值小于3，为便于设计应用，偏安全取n=5。

图10 aj值和n值散点图

综上提出梁格收敛法，具体方法如下：

（1）先按单梁法进行力学计算，并结合实际转体桥梁，计算最大平衡配重比时能调整的偏心值δ，取δ/5作为两次梁格模型的收敛标准。以背景工程为例，外侧斜腹板最大配重1 200 kN，转体自重加配重共145 296.9 kN，距球铰中心10 m，则δ/5=1 200×10/145 296.9/5≈0.017 m，则收敛标准定为0.017 m。

（2）建立子纵梁数等于腹板数的常规梁格模型进行预偏心计算，然后继续增加子纵梁片数进行梁格划分，比较前后两个预偏心值的差值是否小于δ/5，若不满足则继续划分梁格直到满足为止。注意对所有模型的反力进行前后模型的误差对比，误差往往小于0.1%，其目的是通过反力这一指标来发现梁格建模的人为失误。

（3）按最终梁格模型的计算结果作为预偏心值。特别地，当预偏心值小于0.02 m时，因偏心小，易实现配重调平，为方便设计和施工，建议可不设预偏心。

虽然收敛标准n=5是基于矩形截面推导出的，但在实际运用过程中发现，箱形截面更容易满足该收敛标准，这是由于箱梁结构的梁格往往以腹板为子纵梁，而腹板重量占总重量比重较大，因此收敛速度比矩形截面更快，也更易满足收敛标准，在第4节、第5节可以明显看出。

4 等截面斜腹板箱形转体曲线桥

工程中用得最多是箱梁桥，现以本工程0块号支点截面为原型，构建等截面曲线箱梁桥。首先建立单梁模型计算收敛标准采用两次梁格划分法求得预偏心，再建立实体模型，将单支反力和偏心距进行比较。

梁顶面可设置配重1 200 kN，转体自重加配重220 276.7 kN，则收敛标准δ/5=1 200×10/220 276.7/5≈0.011 m。采用桥博V4.3分别建立4纵梁和10纵梁的梁格模型来分别计算预偏心，用ANSYS建立实体模型进行结果校核。模型如图11到13所示，计算结果见表3。

表3 单梁、梁格、实体模型计算结果对比表

图11 划分成4片子纵梁的梁格模型图

图12 划分成10片子纵梁的梁格模型图

图13 ANS YS实体模型图

可以看出，所有模型的反力F几乎相等，且预偏心结果呈收敛趋势，与第3.3节分析的规律一样。10纵梁与4纵梁的梁格偏心距相差0.005 2 m，显著小于0.011 m，故预偏心值为1.668 m。经计算，此次案例中的aj值为0.055，n值为1.06＜5，说明基于大量模型统计得到的n=5的收敛标准是偏于安全的，能满足工程精度要求。

5 本工程的预偏心求解

经过上述的规律总结和方法应用，现计算本工程斜腹板变高曲线箱梁桥的预偏心值。梁顶面可设置配重1 200 kN，收敛标准δ/5=1 200×10/145 296.9/5≈0.017 m。4纵梁和10纵梁的梁格模型如图14所示。计算结果见表4。

图14 梁格模型图

表4 单梁、梁格模型计算结果对比表

可以看出，所有模型的反力F几乎相等，且预偏心结果呈快速收敛趋势。10纵梁与4纵梁的梁格偏心距相差0.001 8 m，显著小于0.017 m，满足工程实际应用。最终本工程的预偏心设置为偏向曲线内侧72 cm。

6 结 语

本文以环市南路上跨广深铁路2×68 m转体桥梁为背景，通过对矩形等截面曲线桥预偏心的理论公式推导，对不同曲线半径、桥宽、桥长和划分子纵梁数的3 600个梁格模型进行计算和对比，得出所有模型的反力几乎相等,子纵梁片数的增加可以极快地减小梁格预偏心误差，且呈绝对收敛趋势的规律。提出梁格收敛法求预偏心，并用该方法对等截面曲线箱梁桥进行计算，同时用实体模型进行验证，结果和规律曲线均十分吻合，最后计算出背景工程的预偏心值。本文的方法可应用于所有转体曲线桥预偏心的计算。