快速路圆曲线超高与横向力系数分配方法研究

董 猛

[上海市政工程设计研究总院（集团）有限公司，上海市 200092]

0 引言

机动车在圆曲线上行驶时，受离心力作用会产生滑移，为抵消车辆在圆曲线路段上行驶时所产生的离心力，保证车辆能安全、稳定、满足设计速度和经济、舒适地通过圆曲线，需要在圆曲线范围内设置的外侧高于内侧的单向横坡，与路面传递的横向摩阻力共同抵消车辆在曲线行驶中产生的离心力。

超高与横向力系数是确定道路线形设计圆曲线半径的重要参数。现行城市道路与公路设计规范仅明确了不设超高圆曲线最小半径和设超高圆曲线最小半径时的超高和横向力系数取值，没有明确圆曲线半径介于两者之间的超高和横向力系数关系，在具体的工程设计中容易导致超高取值标准不一致。

本文通过分析国内现行城市道路与公路路线设计规范在超高设计方面的相关要求，借鉴美国各州公路与运输工作者协会（AASHTO）2018年新版《A Policy on geometric design of highways and streets》（以下简称“AASHTO绿皮书”）中的超高分配计算方法，以城市快速路为例，提出了不同圆曲线半径建议超高值，供设计人员参考。

1 相关概念及术语

为统一概念术语，结合国内外规范和文献，对下列概念、术语及符号进行约定。

（1）横向力系数

横向力是汽车在弯道上行驶时，受离心力的作用，车辆轮胎在路面上产生的横向摩阻力。此横向力与垂直路面的竖向力之比称为横向力系数。横向力系数是设计平曲线半径和超高的最基本的参数，其极限值为横向摩阻系数，主要受路面条件、轮胎材料和气压、车速以及荷载等因素的影响（见表1）[1]。为本文中横向力系数用符号f表示。

表1 横向力系数与行车舒适度的关系

（2）超高

为抵消或减小车辆在平曲线路段上行驶时所产生的离心力，在该路段横断面上做成外侧高于内侧的单向横坡形式，称为平曲线超高[2]。合理设置超高，可全部或部分抵消离心力，提高汽车在平曲线上行驶的稳定性与舒适性。本文中超高用符号e表示，如图1所示。

图1 圆区线上汽车受力分析

圆曲线半径小于规范规定的不设超高圆曲线最小半径时，应在曲线上设置超高。

（3）超高与横向力系数的关系

汽车在圆曲线上行驶时受到重力G、路面支持力N和离心力F的共同作用，离心力F对行驶稳定性有很大的影响。通过设置超高，车辆重力的水平分力可抵消一部分离心力的作用，其余部分离心力由汽车轮胎与路面之间的横向摩阻力与之平衡[2]（见图1）。

通过汽车行驶在圆曲线上的受力模型分析，超高和横向力系数与车速、圆曲线半径之间的关系可用式（1）表示。在给定行驶速度和半径的情况下，超高与横向力的和（e+f）是定值，超高e越小，横向力系数f越大，汽车在圆曲线上的稳定性越差。式（1）对确定圆曲线半径、超高值及评价汽车在圆曲线上行驶的安全性和舒适性具有十分重要的意义。

式中：V为设计速度，km/h；R为圆曲线半径，m；e为超高，即路面横坡度；f为横向力系数。

2 现行规范对圆曲线超高的要求

2.1 公路设计规范对超高的要求

（1）最大超高值

《公路路线设计规范》（JTG D20—2017）规定圆曲线最大超高，一般地区8%，以通行中、小型客车为主的高速公路和一级公路可采用10%，积雪冰冻地区为6%，城镇地区为4%[1]。

（2）不设超高圆曲线最小半径

《公路工程技术标准》（JTG B01—2014）规定不设超高圆曲线最小半径，是按横向力系数f=0.04，超高e=-2.0%（正常路拱横坡2%）代入式（1）计算整理后得出的结果（见表2）[3]。

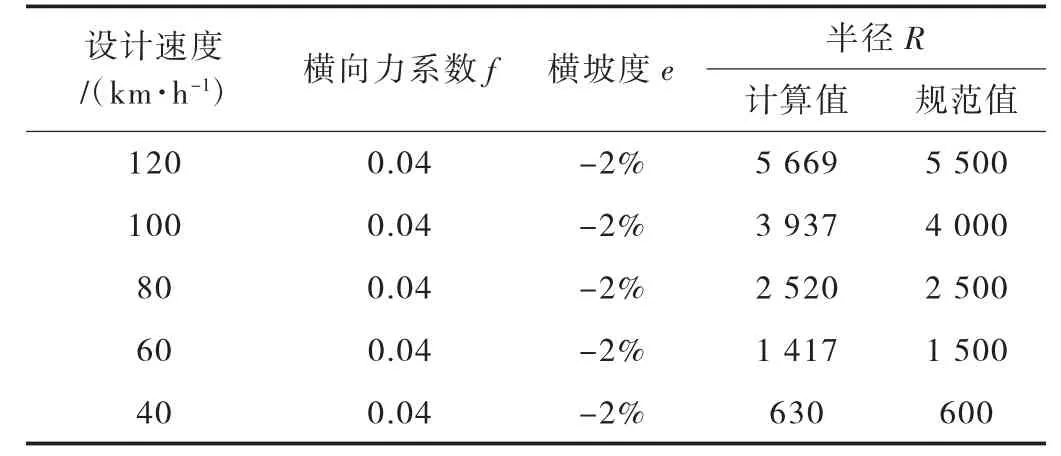
表2 公路不设超高圆曲线最小半径计算

（3）设超高圆曲线最小半径

《公路路线设计规范》（JTG D20—2017）分别给出了圆曲线最小半径的一般值和极限值，两者的区别在于曲线行车舒适性的差异。在设计速度确定的情况下，圆曲线最小半径取决于横向力系数和超高的选值。

在确定圆曲线最小半径一般值时，横向力系数f取0.05~0.06，超高e取6%~8%，代入式（1）计算整理（见表3）[1]。

表3 公路超高圆曲线最小半径一般值计算

在确定圆曲线最小半径极限值时：横向力系数f取0.10~0.17，速度高取低值，速度低取高值；超高e取4%~10%，代入式（1）计算整理（见表4、表5）。为便于和城市道路设计规范对照，本文中仅列出了最大超高4%和6%两种情况。

表4 公路设超高圆曲线最小半径极限值计算（最大超高4%）

表5 公路设超高圆曲线最小半径极限值计算（最大超高6%）

2.2 城市道路设计规范对超高的要求

（1）最大超高值

城市道路的最大超高按照不同的设计速度确定。考虑到受交叉口、非机动车以及道路两侧地块建筑影响，除快速路以外，其他的城市道路不宜采用过大的超高横坡度。

《城市道路路线设计规范》（CJJ 193—2012）规定最大超高，设计速度100 km/h、80 km/h时为6%，设计速度60 km/h、50 km/h时为4%，设计速度小于或等于40 km/h时为2%[4]。

（2）不设超高圆曲线最小半径

《城市道路路线设计规范》（CJJ 193—2012）中规定的不设超高圆曲线最小半径，是按横向力系数f=0.67，超高e=-2.0%，代入式（1）计算整理后得出的结果（见表6）。

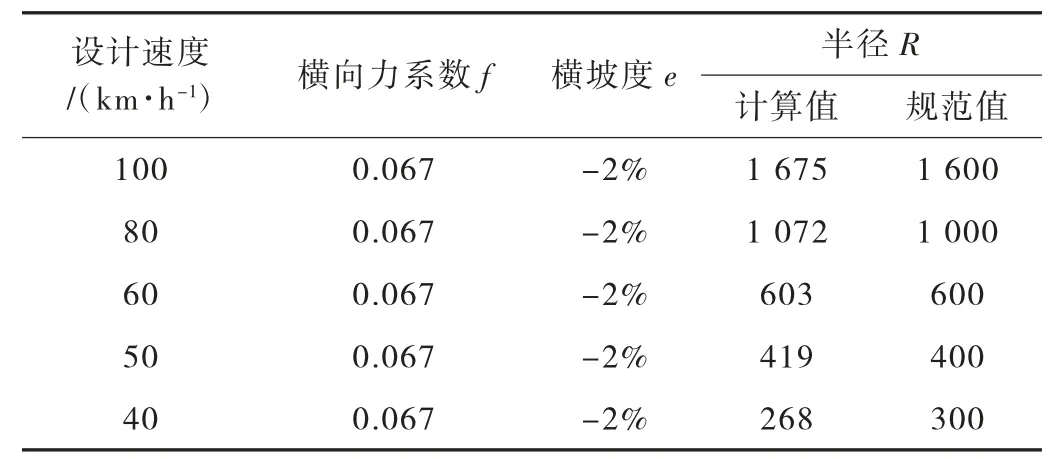
表6 城市道路不设超高圆曲线最小半径计算

（3）设超高圆曲线最小半径

城市道路圆曲线最小半径一般值，是按横向力系数f取0.067，超高e取2%~6%，代入式（1）计算整理（见表7）。

表7 城市道路设超高圆曲线最小半径一般值计算

在确定圆曲线最小半径极限值时，横向力系数f取0.14~0.16，速度高取低值，速度低取高值；超高e取2%~6%，代入式（1）计算整理（见表8）。

表8 城市道路设超高圆曲线最小半径极限值计算

2.3 小结

（1）在圆曲线超高设计中，超高和横向力系数两个变量存在负相关性。在给定行驶速度和半径的情况下，超高与横向力的和（e+f）是定值，超高e越小，横向力系数f越大，反之亦然。确定圆曲线超高值应先确定横向力系数。

（2）现行公路与城市道路设计规范分别对不设超高圆曲线最小半径、设超高圆曲线最小半径一般值及极限值等3种情况，明确了超高和横向力系数取值标准；对于圆曲线半径介于三者之间的情况，规范均未明确横向力系数取值，不同圆曲线半径的超高值需设计人员计算。《公路路线设计规范》（JTG D20—2017）在条文说明中重新补充了最大超高值10%、8%、6%和积雪冰冻地区条件下，路拱横坡采用2%时，经计算获得的不同圆曲线超高值。

（3）现行公路与城市道路设计规范均采用设计速度计算超高值。公路设计规范要求在必要时按运行速度进行验算。

3 美国AASHTO绿皮书超高分配方法

AASHTO绿皮书是美国各州公路与运输工作者协会出版的一本设计指南，通常被视为美国公路与城市道路几何设计的标准，也是国际上公认的道路线形设计的权威著作。本节内容引用自2018年出版的AASHTO绿皮书第7版，供设计人员学习参考。

3.1 不设超高横向力系数

AASHTO绿皮书中的正常路拱横坡与国内规范一致，取1.5%~2.0%。不设超高横向力系数取0.033~0.048，接近公路设计规范要求，较城市道路设计规范要求低。

3.2 最大横向力系数

AASHTO绿皮书针对不同设计速度，测定了最大横向力系数fmax（见表9）[5]。

表9 AAS HTO绿皮书最大横向力系数

3.3 最大超高

AASHTO绿皮书中最大超高分别为4%、6%、8%、10%、12%五档，合理的最大超高不超过8%，城市地区的最大超高一般为4%~6%。

3.4 超高和横向力系数分配方法

在AASHTO绿皮书中，列出了五种超高和横向力系数分配的方法，如图2所示[5]。横轴为曲率（即半径的倒数，1/R），纵轴为超高e或横向力系数f。

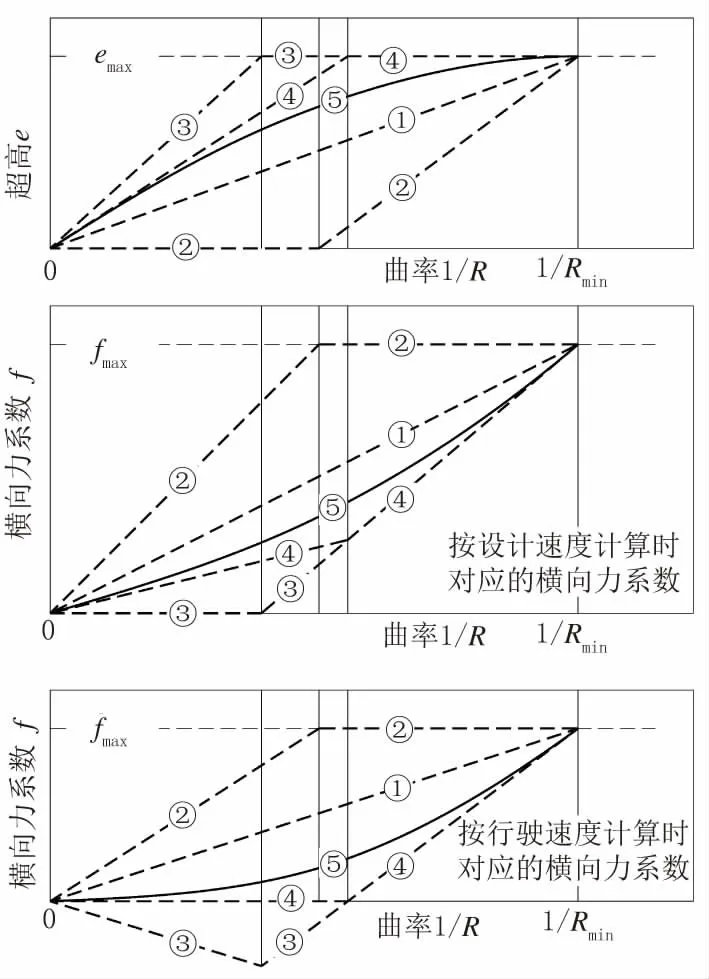
图2 AAS HTO绿皮书横向力系数和超高分配方法

第①种方法：超高e和横向力系数f随着曲率的增大而线性增加，在曲率最大处（1/Rmin）设最大超高emax，横向力系数达到最大fmax。

第②种方法：汽车在曲率小的圆曲线（大半径圆曲线）上依靠侧向摩阻提供向心力，直到横向力系数达到fmax；对于更小半径的圆曲线，横向力系数维持fmax，利用超高平衡剩余的离心力，直到超高达到emax。

第③种方法：与第②种方法相反，汽车在曲率小的圆曲线上依靠超高提供向心力，直到超高达到emax。对于更小半径的圆曲线，超高维持emax，利用侧向摩阻的离心力，直到横向力系数达到fmax。

第④种方法：与第③种方法类似，采用比设计速度略小的运行速度进行超高分配，不同设计速度对应的运行速度（见表10）。

表10 AAS HTO绿皮书设计速度与运行速度对照表

第⑤种方法：介于第①种与第④种之间，采用非对称抛物线型的分配方法，是AASHTO绿皮书推荐的超高分配计算方法，计算原理如图3所示。

图3 AAS HTO绿皮书横向力系数及超高计算图示

图3中横轴为曲率（即半径的倒数，1/R），纵轴为超高e或横向力系数f，两条直线分别代表基于设计速度的超高和横向力系数（e+f）D，基于运行速度的超高和横向力系数（e+f）R；两条曲线分别代表不同曲率下计算的横向力系数f曲线和超高值e曲线，其中横向力系数f曲线为不对称抛物线，超高e=（e+f）D-f。具体计算步骤如下[5]：

（1）根据式（1）计算（e+f）D

（2）计算最小圆曲线半径Rmin

式中：VD为设计速度，km/h；fmax为最大横向力系数，查表9。

（3）计算交点PI对应的半径RPI和竖距hPI

式中：VR为运行速度，km/h，查表10。

（4）计算不对称抛物线f曲线的切线斜率

切线①斜率：S1=hPI·RPI

切线②斜率：

（5）计算不对称抛物线f曲线的外距MO

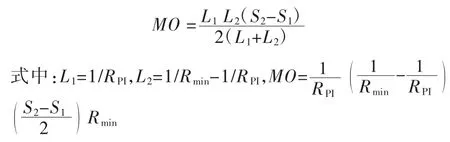
（6）计算不同半径R对应的横向力系数f和超高值e

根据抛物线公式：

式中：x为横轴；Y为f曲线的竖距。

a.当R＞RPI时：

4 快速路圆曲线超高分配及建议超高值

4.1 参数标定

（1）运行速度参照AASHTO绿皮书取值。

（2）不设超高横向力系数按《公路路线设计规范》（JTG D20—2017）取值。

（3）最大超高按《城市道路路线设计规范》（CJJ 193—2012）取值，考虑到快速路连续流交通特性，设计速度60 km/h的最大超高按6%取值。

（4）最大横向力系数以《城市道路路线设计规范》（CJJ 193—2012）为主，设计速度100 km/h对应的横向力系数参照AASHTO绿皮书调整为0.12。

表11为城市快速路圆曲线超高计算参数。

4.2 快速路圆曲线超高建议

采用上述约定的参数，按照AASHTO绿皮书计算方法，计算整理城市快速路圆曲线超高建议（见表12）。

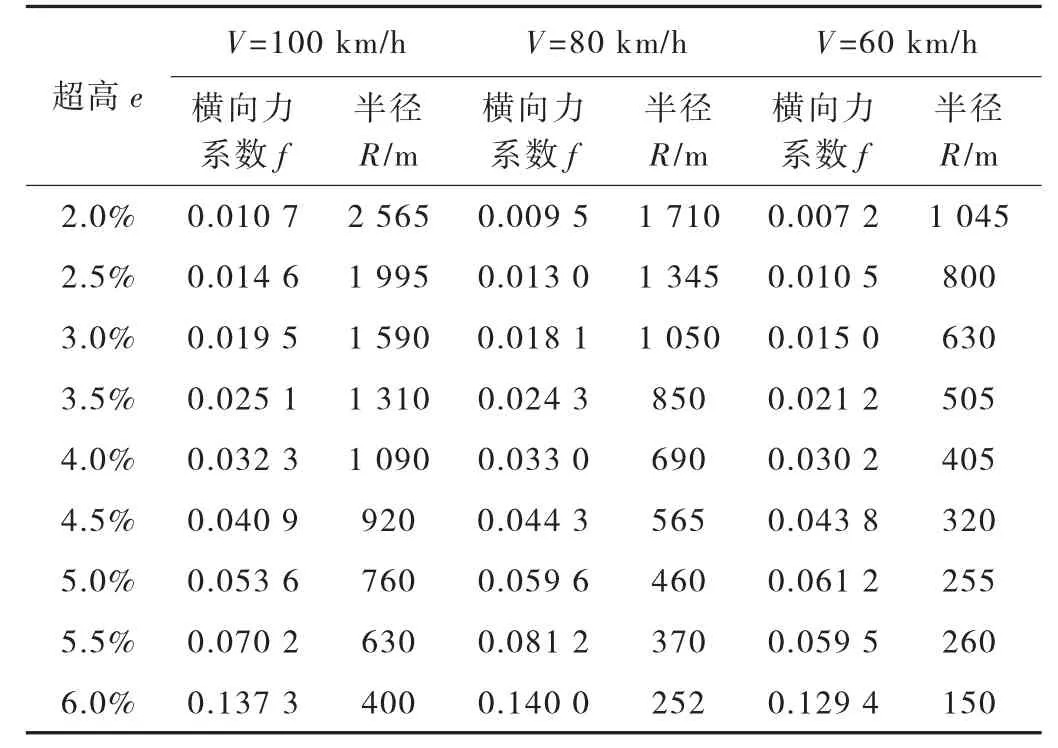
表12 快速路超高对应的最小圆曲线半径（emax=6%）

5 结语

本文采用美国各州公路与运输工作者协会（AASHTO）2018年新版《A Policy on geometric design of highways and streets》中的超高分配计算方法，提出了城市快速路不同圆曲线半径建议的超高值，弥补过往凭工程经验进行超高计算的不足，计算结论可供相关工程技术人员参考。