深圳市燕罗人行桥人致振动分析与控制研究
2022-09-23倪健
倪 健
[同济大学建筑设计研究院(集团)有限公司,上海市 200092]
0 引言
随着我国社会发展,城市建设需求由量向质转型,许多位于城市中心的人行桥已经不仅是实现交通功能的结构物,还是一座体现城市文化、城市主题的建筑艺术品。在追求人行桥的附加景观艺术需求时,大跨纤柔、空间异形的桥梁结构越来越多。随之而来,人行桥的动力问题逐渐成为结构设计的控制因素。然而,我国《城市人行桥与人行地道技术规范》(CJJ 69—1995)仅对人行桥的竖向自振频率加以约束,要求竖向自振频率不应小于3 Hz。对于大跨纤柔、空间异形的人行桥而言,这一要求是难以满足的。在国内外学者的研究以及其他国家的现行人行桥设计指南[1]中,仅粗略地对人行桥的竖向基频加以限制,这是存在一定问题的,因为评价桥梁动力特性时应该以人行舒适度作为指标。本文以深圳市燕罗人行桥工程为背景,采用人行舒适度作为评价指标,对大跨度人行桥人致振动控制设计方法进行研究。
1 人行桥动力设计方法
1.1 人行桥动力设计流程
人行桥动力设计的流程见图1。

图1 人行桥动力设计流程图
1.2 频率敏感范围
结合国内外学者的研究,当桥梁固有频率落在敏感频率范围时需要进行动力响应分析,其中竖向振动敏感频率范围为1.25~3 Hz,横向振动敏感频率范围为0.5~1.2 Hz[2]。
1.3 行人动载模型
人的行走是连续且具有周期性的,行走时人的重心上下起伏,对地面产生周期性竖向荷载。两脚行走时交替的过程,会产生周期性的水平侧向动载。工程实践中一般采用确定性的行人动载模型FP(t),用傅里叶级数表达,为静载和多阶简谐动载之和的形式[2]:

式中:W为平均行人重量,N;fp为行人步频,侧向取一半,Hz;αi为第i阶动载系数;φi为第i阶动载相位;t为时间。
在国外的设计指南中,一般竖向仅考虑1阶到2阶动载,横向仅考虑1阶动载。本文行人动载模型采用德国人行桥设计指南EN03,其行人动载模型p(t)为:
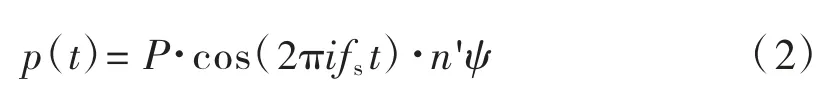
式中:n'表示桥上同步行走的等效人数,人/m2;P为1阶荷载幅值(竖向取280 N,横向取35 N);fs为桥梁敏感模态频率;ψ为考虑频率范围的折减系数(见图2)。

图2 折减系数
加载面积为S时,等效行人数n'取值为:
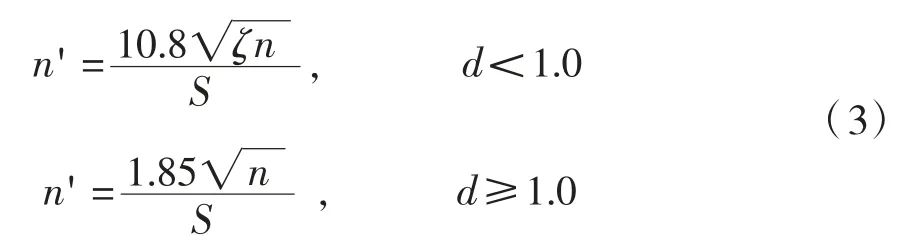
式中:ζ为结构阻尼比;n表示加载面积为S时的行人数;d表示行人密度,人/m2。
1.4 结构阻尼比
人行桥舒适性设计是一种使用状态性能指标,可采用表1数值用于舒适性设计时的最小阻尼比和平均阻尼比。

表1 舒适性设计结构阻尼比经验值
1.5 侧向锁定
锁定现象系指当结构产生横向振动时,不同相位、不同频率的行人因相互影响而导致激励趋同,使得振动加剧的现象[3]。
德国等的人行桥动力设计指南均采用了Dallard等的研究成果。对于频率小于1.2 Hz的横向振动,当产生较大振幅(加速度大于0.1~0.15 m/s2)时,通过计算结构保持动力稳定的最大行人数,检算横向振动的侧向锁定,最大行人数Nmax计算公式为:
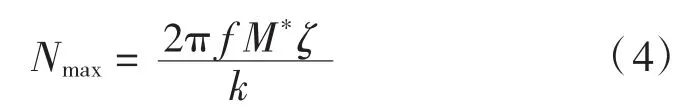
式中:f为固有频率;k为负阻尼系数常量,300 N·s/m;M*为模态质量;ζ为结构阻尼比。
1.6 舒适度评价指标
根据国内外学者研究,舒适度指标大多采用加速度来表示,本文舒适度评价指标参考德国人行桥设计指南EN03。
行人舒适度评价标准见表2。

表2 行人舒适度评价标准
2 工程概况
燕罗人行桥位于深圳市宝安区燕罗街道,现状松罗路桥上游约630 m处,呈南北走向。主桥拱脚分别与南北两侧堤顶路接顺,主梁预留空间。远期考虑跨越沿河市政道路与企业接驳,服务于两侧工业园区。
燕罗人行桥主桥采用14 m+108 m+14 m斜拉-拱桥组合体系,桥梁总长136 m。桥梁宽度11.5 m,横断面布置为0.25 m栏杆+11 m人行道+0.25 m栏杆。上部主梁段宽度5 m,断面布置为0.25 m栏杆+4 m人行道+0.25 m栏杆。主拱矢高9.2 m,矢跨比1/11.74,采用分离式钢箱截面,截面高度1.2 m,拱脚通过PBL剪力键与混凝土拱座连接。塔为混凝土结构。塔与主索、背索共面,与竖直面夹角12°。主梁采用钢板梁截面,立柱为钢结构。
燕罗人行桥立面图见图3。

图3 燕罗人行桥立面图(单位:cm)
3 人致振动分析及控制
3.1 动力特性
根据有限元计算结果,燕罗人行桥前7阶振型(频率3 Hz以内)见图4~图10。

图4 第1阶:拱梁1阶侧向正对称(1.77 Hz)

图10 第7阶:主梁局部侧飘(2.76 Hz)
根据1.2节敏感频率的范围以及1.5节侧向锁定验算前提,横向模态均未落在敏感频率范围内,即本工程无需进行侧向动力响应分析及侧向锁定检验分析。竖向1阶反对称模态(第2阶,频率1.86 Hz)和竖向1阶正对称模态(第4阶,频率1.91 Hz)落在了竖向敏感频率范围1.25~3 Hz范围内,以下将对此2个模态进行动力响应分析。

图5 第2阶:拱梁1阶竖向反对称(1.86 Hz)

图6 第3阶:桥塔侧飘(1.90 Hz)

图7 第4阶:拱梁1阶竖向正对称(1.91 Hz)

图8 第5阶:拱梁2阶侧向正对称(1.93 Hz)

图9 第6阶:连接跨主梁侧飘(2.76 Hz)
3.2 动力响应分析
针对竖向1阶反对称模态(下称反对称模态)和竖向1阶正对称模态(下称正对称模态)分别进行动力响应分析。
反对称模态最大响应加速度值为3.9 m/s2,位于拱跨四分点位置处(见图11);正对称模态最大响应加速度值为4.8 m/s2,位于拱跨跨中位置处(见图12)。考虑桥梁人行设计流量大,本工程设计荷载工况为1.5 P/m2(交通繁忙)的工况下,行人的舒适度能够保证满足CL2(中等)等级以上。据此标准,结构正对称模态和反对称模态动力响应舒适度等级为CL4,行人舒适度已达不能接受的程度。

图11 反对称模态四分点加速度响应
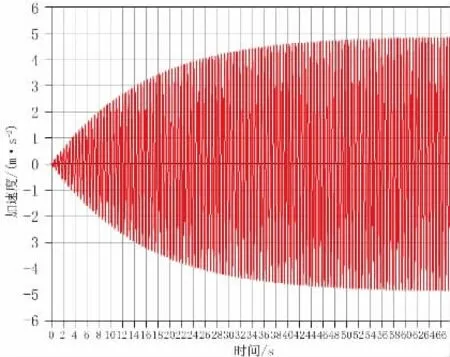
图12 正对称模态跨中加速度响应
3.3 调谐质量阻尼器(TMD)减震设计
3.3.1 TMD参数取值
TMD质量与减震模态广义质量的比值一般取0.01~0.05。考虑人行动载模型为简谐荷载,响应目标为加速度,TMD的最优频率比αopt计算公式见式(5),最优阻尼比ζopt计算公式见式(6)[2]。
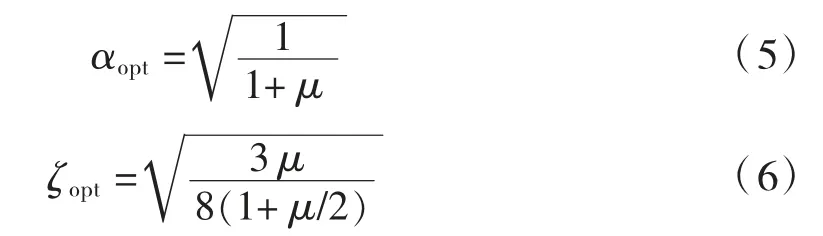
根据式(5)、式(6),TMD布置情况及相关参数见表3。

表3 TMD布置及相关参数表
考虑振动控制的效率,结合上述公式计算,TMD布置方案为:在正对称模态动力响应敏感的跨中位置设置1个7 t的TMD;在反对称模态动力响应敏感的2个四分点位置各设置1个3 t的TMD。
3.3.2 动力响应分析
加装TMD后,反对称模态最大响应加速度为0.51 m/s2,位于拱肋四分点位置,舒适度等级为CL2(见图13);正对称模态最大响应加速度为0.45 m/s2,位于拱肋跨中位置,舒适度等级为CL1(见图14)。行人舒适度等级为中等以上,满足设计目标。

图13 反对称模态四分点加速度响应(加装TMD后)
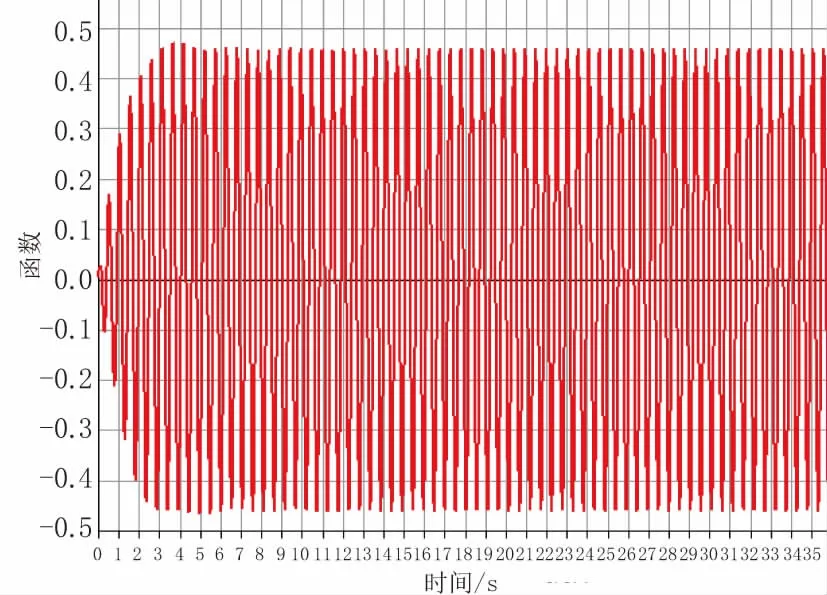
图14 正对称模态跨中加速度响应(加装TMD后)
3.3.3 TMD减震效果对比
设置TMD前后的人行桥动力响应对比见表4。
由表4可见,加装TMD后,有效控制了人行桥的动力响应,行人舒适度得到明显提高。

表4 减震效果对比
4 结语
(1)国内人行桥设计规范关于人行桥动力设计内容较为简单苛刻,不适应国内大跨度纤柔的人行桥设计需求。
(2)当大跨度人行桥固有频率落在人行敏感频率范围内时,可通过设置调谐质量阻尼器来有效降低结构的动力响应。
